在初中数学教学中培养学生问题意识的实践研究
2017-05-03王家雄
王家雄
摘要:培养学生的问题意识是新课程的重要教学理念。然而,在当前数学课堂教学中,学生问题意识薄弱。本文提出并论述了数学课堂中如何培养学生“敢问”“想问”“会问”“善问”的策略,以促进学生问题意识的形成,达到“以问促学”的最终目的。
关键词:数学教学;问题意识;培养
中图分类号:G633.6 文献标识码:A 文章编号:1992-7711(2017)02-0031
近代著名教育家陶行知曾在一首诗中写道:“发明千千万,起点是一问。智者问得巧,愚者问得笨。人力胜天工,只在每事问”。可见,问题意识在思维过程和创新活动中占有非常重要的地位。初中数学是一门培养学生思维和方法的基础学科,问题是它的灵魂。因此,在数学教学中,教师要从学生的角度出发,引导学生主动质疑,使学生敢于提问、善于提问。只有这样,学生的思维才能充分在课堂教学中展现出来,才能形成知识迁移与运用,才能有解决问题的思想、方法,学生的学习积极性才能被真正调动起来,变“要我学”为“我要学”。
然而,在实际教学中,发现学生的问题意识还是比较薄弱,有的学生根本没有想过在课堂上根据教学内容向教师提出问题;有的学生不敢提问题;有的学生不能提出有效的问题,所提出的问题质量不高。本文结合笔者多年数学教学中的一些经验,就如何提高数学问题意识作初步探讨。
一、营造“提问”情感氛围——让学生“敢问”
在数学课堂教学中,学生不向教师提问的一个重要原因是不敢。怎样消除学生思想上的顾虑,使他们积极、大胆地参与到学习中,是教师应该研究和探讨的首要问题。
教师作为教学气氛创设和保持的主导者,应尊重学生的人格与个性,对全体学生要平等对待、一视同仁。在课堂上,要设法营造积极、宽松的课堂气氛,建立民主、和谐的师生关系,为学生建立没有批评指责、允许失败的宽松环境,鼓励学生敢于思考、敢于说、敢于问,无论问得正确与否、质量的高低,都应给予热情的鼓励和真诚的表扬,帮助他们树立敢于质疑的自信心。
另外,教師在组织教学中不必害怕驾驭不了课堂秩序和解决不了学生提出的问题,从而会贬低自己在学生心目中的形象和声誉,在教学中不能过于威严、专制,否则学生不敢表达自己的问题和见解。
二、设计有效教学情境——让学生“想问”
学生在课堂上不愿意提问的原因有的是对数学缺乏兴趣,有的是缺乏适当的问题情境,学习的积极性没有被调动起来,在课堂上不动脑子,只是被动地接受。对于这部分学生,教师在组织教学时要有意识地创设有效的情境,培养学生学习的兴趣,促使学生质疑、提问、探索求解。
1. 创设问题情境,让学生“想问”
在课堂上有意识地创设问题情境,培养学生质疑的兴趣,以趣生疑,由疑引发好奇心,由好奇心引发积极思考,进而促进学生不断地发现问题。比如,在学习“一元二次方程根与系数的关系”一节内容时, 可安排这样的游戏:让学生说出某一元二次方程的两根及二次项系数,由教师猜出方程。一、二、三……结果被猜中,学生觉得真奇怪,教师怎么知道我们出的方程?这就激起学生的疑问,感觉一元二次方程的根与系数之间似乎存在某种关系,也就激发了学生质疑探究的积极性。
2. 设置认知冲突,让学生“想问”
教师要根据学生的已有知识经验来安排教学内容,引发学生已有知识经验与未知之间的冲突。通过引发冲突,可以激发学生对新学内容的兴趣,使学生产生要学的动机。在这一过程中,教师要善于发现学生学习的困难,引导他们对学习困难进行描述,使之清晰地成为学生的认知冲突。同时,通过恰当的引导,引发学生生成新的问题。比如,在教因式分解法解一元二次方程时,笔者设计下表所示的步骤教学:
通过比较,学生不约而同地提出:“方程的根为什么会少了一个?”教师问:“看你们的解题过程,两边同除以x-3的数学依据是什么?”有学生说:“等式的两边同乘以或除以相同的数,等式仍然成立。”教师又问:“是这样的吗?”又有学生补充“两边同乘以或除以相同的数不能等于零。”教师问:“两边能同除以x-3吗,你发现了什么问题?”学生在教师的引导下发现了新的问题:解方程时一般不能两边同除以含有未知数的代数式,因为这样的代数式可能等于零。
三、提供适当提问载体——让学生“会问”
在教学中,教师可以充分挖掘、改编、整合教学内容,为学生提问提供载体,利用载体并结合学生的兴趣点、知识的疑难点、思维的发散点进行设问,让学生自己去学习、探索、发现问题,进而引发学生自己提出问题。
1. 巧用改编的习题,使学生“会问”
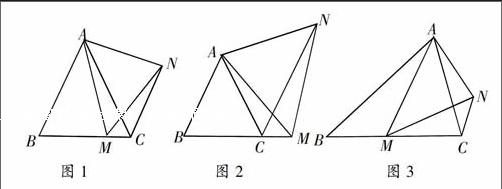
教师在教学过程中,可对课本中的例题、习题或中考题进行适当改编,对训练学生的思维,培养学生的问题意识有很好的效果。比如,2013年衢州市中考题22题(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN,求证:∠ABC=∠ACN。
如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其他条件不变,请你至少提出两个数学问题,并说明理由。
如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC。连结CN,请你至少提出两个数学问题,并说明理由。
问题(2)(3)改编了结论,请学生至少提出两个数学问题,并说明理由。通过改编,问题更加开放,有利于学生的知识迁移与应用。学生的思维在课堂上得到充分的展现,有利于学生解决问题的思想、方法的形成。
2. 利用知识内在联系,使学生“会问”
教师可以利用知识的内在联系,启发学生多角度提问题。如复习二次函数时,教师呈现二次函数y=x2-6x-7后提问,你能尽可能多地提出与此函数有关的数学问题吗?学生通过认真思考,提出很多数学问题。如:(1)求函数图像的顶点坐标、对称轴、开口方向?(2)求函数的增减性?(3)求本函数y=x2-6x-7是由y=x2的图像经过怎样平移得到的?(4)求函数y=x2-6x-7与坐标轴的交点坐标?(5)求自变量在什么范围内,函数值大于零、小于零?(6)求图形中相应三角形的面积?(7)观察图像确定y=x2-6x-7方程的解?
以问题串形式组织教学,能够发展学生的探究能力,培养学生的提问题能力,拓展学生的思维深度与广度,同时又有利于学生数学知识体系的自我构建。
四、提高学生提问质量——让学生“善问”
一些学生在数学学习中虽然会提问题,但提的是一些质量不高、甚至是低级的问题。教师应对学生的提问加以引导,把他们的问题引到与教学有关的重点和难点上,使他们的问题提得巧妙、提得有价值。这就要求教师精心设计课堂教学,通过训练,逐步提高学生的提问质量。
1. 在学生思维障碍处,培养学生“善问”
在组织课堂教学时,学生对于教师所给出的问题或习题,经过认真思考、分析,不同的学生往往有不同的想法或解决方法,当自己的想法与他人不相同时,就会有展现自我想法的強烈欲望,会提出困惑内心的问题。此时,教师要善于抓住这一契机,给足时间,让学生说出自己的想法。同时,教师要对这些问题的有效性及时进行分析、评价,只有这样不断训练,学生才能提出深刻有效的问题。
2. 在知识的结合点上,培养学生“善问”
数学知识具有系统性的特点,新知识的学习是建立在已有知识经验基础之上的,新旧知识之间有一定的内在联系,因此,找准新旧知识的生长点极为重要。如在学习菱形时,根据学生已掌握矩形的性质的同时,教师做如下设计:(1)复习旧知识:矩形有哪些性质?(2)请你结合图形观察、发现菱形有哪些性质吗?并加以说明。学生通过观察、思考、分析、对比,自主发现菱形的性质。在课堂教学中,教师经常让学生运用这一方法,今后对类似的问题能自主通过改变问题的属性,提出更多有价值的问题。
3. 在知识的关键点上,培养学生“善问”
教师在组织课堂教学之前,要关注学生的课前预习,学生通过预习,会发现自己认知难点,也就是学生在学习上阻力大、难度高的关键所在,这些地方学生不易理解掌握。教师在课堂上要引导学生大胆地提出自己的问题,只有通过这样不断训练,学生才能提出有质量的问题。
总之,学生问题意识的培养是数学教学的一项重要任务。教师不仅备课时要从不同角度考虑学生可能会有哪些疑问,而且要关注课堂教学中的生成性问题,给足学生提问和质疑的空间。不要为了教知识而讲授知识,而是要把培养学生的创新精神和实践能力作为数学教学的重点,引导学生质疑、探究,体验自主学习、主动参与的乐趣,使学生真正成为学习的主人。
(作者单位:浙江省江山市城东实验学校 324100)
