改进包络模型的GNSS完好性监测阈值设计

吕浩源, 张 辉, 庞春雷, 曹海霞, 王祝欣

(1 空军工程大学信息与导航学院, 西安 710077; 2 93115部队, 沈阳 110000)

0 引言

随着全球卫星导航系统(global navigation satellite system,GNSS)的迅速发展,对其完好性监测越来越重要。卫星导航完好性是指当系统不可用于导航时向用户提供告警的能力[1],基本原理是:地面参考站计算伪距差分改正数和伪距测量误差标准差,并通过数据链路播发至用户端计算出相应的完好性监测阈值[2],将其与故障门限比较从而判断系统的可用性。伪距测量误差标准差直接影响完好性监测阈值的大小,因此准确估计出标准差非常有必要。

传统包络模型一般假设修正误差满足零均值的高斯分布,并且其尾部可以用标准差膨胀的方法进行包络。但由于多路径误差和观测噪声的影响,传统模型无法有效对此类误差进行包络,较大的非零均值、非高斯误差都将导致标准差膨胀过大,将会降低系统的完好性监测水平[3]。为有效抑制修正误差对完好性监测的影响,国内外学者开展了标准差估计和阈值计算的相关研究。最早DeCleene提出用sigma膨胀算法来估计系统完好性监测阈值[4],但其建立的估计模型要求修正误差满足单峰对称的高斯分布。当修正误差偏差较大时,需要较大的sigma膨胀系数来保证包络模型将尾部误差完全覆盖,这就扩大了标准差,降低了完好性监测水平。文献[3]分析了用户端定位加权矩阵对伪距修正误差的影响,通过引入不同卫星间相关性非高斯标准差,改变了传统加权矩阵系数,有效降低了得到的阈值,从理论上确定了膨胀系数,但该方法在不同类型误差的膨胀系数选择上仍然存在一定困难。文献[5]建立了两种包络模型,并且针对不同包络模型特点进行了适用性分析,但两种模型都是基于一定分布假设条件下的,有待开展针对实测数据的模型验证。目前开展的各种膨胀算法在满误差覆盖同时,都存在因膨胀系数选取不当导致系统可用性水平降低的问题[6]。因此设计出一种合理的误差包络模型,准确估计出误差的标准差,对完好性监测阈值设计具有非常重要的意义

文中在分析传统误差包络模型的基础上将多路径误差模型化,并建立了一种新的包络模型,通过与传统的高斯包络模型对比可得:改进的包络模型可以有效减小估计的标准差,从而减小完好性监测阈值。实验还证明改进包络模型得到的完好性监测阈值能够有效降低漏警率。

1 高斯包络模型的完好性监测阈值设计

高斯概率包络是指采用高斯分布模型对受污染分布的误差模型进行概率包络。通过对伪距修正误差概率分布函数进行覆盖,估计伪距修正误差的标准差,从而计算系统的完好性监测阈值。文中将以完好性监测中的垂直保护级VPL作为故障监测阈值进行对比分析。

1.1 垂直方向故障监测阈值计算

根据定位解的表达式,用户可按方差传递的方法将伪距域完好性信息转换到定位域。转换计算时可作如下假设:H0为地面参考站无故障影响。如果假设H0成立,且地面参考站提供的伪距修正误差服从零均值的高斯分布,则用户垂直方向定位误差保护级为[3]:

(1)

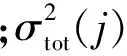
1.2 高斯包络及阈值设计

高斯包络及阈值设计主要分为以下步骤:

Step 1:载波相位平滑伪距。载波相位平滑伪距可以减小伪距测量中的粗大误差,提高测量数据的精确度。基本原理是对每个信道的观测量进行Hatch滤波[9]:

(2)

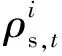
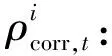
(3)

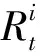
Step 4:高斯膨胀。将标准的正态分布绘入到Step3中得到概率密度分布图中,将已有的标准正态分布进行膨胀,直至由数据所得的离散的概率密度函数能够被完全包络,从而得到膨胀后的σtot(j)值。

Step 5:垂直方向保护限值生成。将经过膨胀后的σtot(j)值代入式(1)中,即可得到基于正态分布假设条件下的完好性监测限值VPL。

图1 高斯膨胀算法sigma估计

2 改进包络模型的完好性监测阈值设计

传统高斯膨胀算法的sigma估计是基于伪距修正误差符合零均值的高斯分布开展的,由于受多路径效应的影响,传统模型无法有效的对sigma进行估计,因此文中将建立一种基于非正态分布下的sigma估计,从而得到更加准确的完好性阈值。

2.1 非正态分布误差模型的建立

多路径的影响一直是制约卫星导航系统完好性监测的重要因素,由于其变化情况非常复杂,受反射率、天线高度、卫星仰角和接收机相关器的相关间隔等多种因素影响。根据目前的相关研究可知,多路径误差是非零均值、非高斯的,基于此文中将通过对多路径误差建模的方法来评估其对完好性监测阈值的影响,根据文献[7],多路径误差模型为:

e=μ+cacosθ

(4)

式中:e为伪距测量中的多路径误差;μ为多路径误差的非零偏差项;cacosθ为多路径的非高斯项,c=min[2hsinE,d],d为相关器步长的一半,h为接收机天线高,E为卫星仰角,a为信号反射率,θ为相对直射信号的相位延迟。

2.2 改进包络模型的完好性阈值设计

根据多路径信号的特征,建立一种改进包络的标准差估计模型,该模型可以在有效包络误差的基础上,减小估计的标准差。假设a在[0,m]上是均匀分布的,θ也满足均匀分布,根据联合概率分布可推导出多路径误差模型[7]的概率密度函数为:

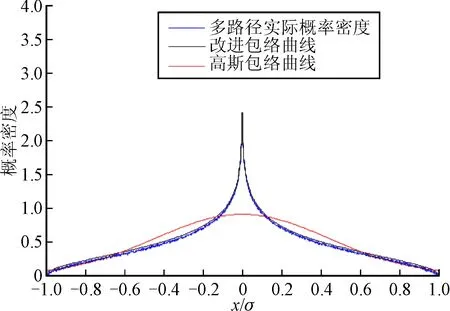
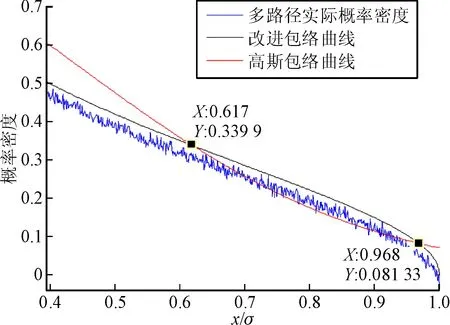
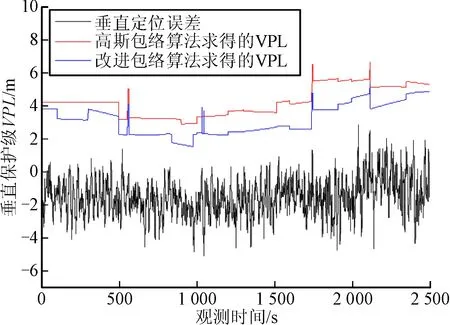
∀|x|

(5)

根据概率密度函数可得概率分布函数:

(6)

当传统的概率包络无法满足条件时,根据多路径误差模型,考虑到非零偏差影响,建立新的完好性监测阈值表达式:

(7)

3 试验及分析

按照多径模型构建随机变量,设定z=acosθ,并且a和θ分别满足在区间[0,m]和[0,2π]上的均匀分布,c为常数项,为便于分析计算,将m和c设定为1。如图2所示,蓝色实线为多路径概率密度,通过高斯包络得到的σ为0.441,而改进包络模型得到的σ为0.410,仿真说明对于多路径误差影响,改进包络模型可以减小因高斯膨胀过大带来的sigma误差;此外通过观察图3,根据曲线的对称性可知在(0.622,0.969)区间和(-0.969,-0.622)区间改进包络模型的包络特性明显优于传统的高斯包络模型,说明改进包络模型的尾部包络特性优于高斯包络。图4中两种包络方法的概率分布均由0变到1,说明两种概率分布都可以实现对误差的完全包络,证明了两种包络模型的有效性。

图2 改进包络与高斯包络概率密度对比

图3 放大的改进包络与高斯包络概率密度对比

图4 改进包络与高斯包络概率分布对比

在仿真证明模型的优越性后,将开展基于实测卫星数据的实验。实验采用2016年3月26日15时起接收机连续接收的2 500 s数据,实验地点为西安市莲湖区某高楼楼顶,开展实验时卫星可视状况良好,可同时观测到仰角大于5°的GPS卫星有8颗。图5中黑色实线为接收机高度定位误差,将不同包络模型下得到的标准差代入式(7),红色实线为高斯包络模型得到的完好性监测阈值,蓝色实线为改进包络算法得到的完好性监测阈值,通过对比可以发现改进包络模型得到的保护阈值VPL明显小于高斯包络方法得到的保护阈值,证明了方法的有效性,此外还说明改进包络算法在减小漏警率方面的可能。

图5 两种方法的阈值对比

为验证改进包络模型对漏警率的影响,选取不同区间σ值做不同模型下漏警率对比分析,分别选取相同阈值和相同方差的不同分布,当阈值取不同倍数σ时,漏警概率也会变得不同。由表1可知随着σ值变大,两种方法得到的漏警概率都会相应的变小,但当阈值选取大于2.5σ时改进包络模型的漏警率明显低于高斯包络模型。又因为完好性关注[3σ,∞)区间,对于多路径误差,改进包络模型的完好性监测水平将明显优于传统高斯膨胀模型。

表1 不同包络模型漏警率对比

4 结论

跟据多路径对完好性监测的影响,提出了一种适用于多路径误差的改进包络模型。相对于传统包络模型,改进包络模型可以得到更小的标准差值,从而有效的减小了完好性监测阈值VPL和完好性监测系统漏警率,提高了完好性监测水平。下一步将开展针对不同机场环境下的多路径误差模型研究,以便有效克服不同场地环境下多路径效应对完好性监测的影响。

参考文献:

[1] 张军. 空域监视技术的新进展及应用 [J]. 航空学报, 2011, 32(1): 1-14.

[2] 李斌, 王党卫, 杨明. 一种地基增强系统(GBAS)B值的分析与处理技术 [J]. 现代导航, 2013(1): 19-23.

[3] 李亮, 赵琳, 丁继成, 等. 提高LAAS空间信号可用性的完好性监测新膨胀算法 [J]. 航空学报, 2011, 32(4): 664-671.

[4] DeCleene B. Defining pseudorange integrity-overbounding [C]∥Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2000: 1916-1924.

[5] 牛飞, 陈金平, 高为广, 等. 非正态分布假设下的完好性阈值计算与分析 [J]. 武汉大学学报(信息科学版), 2012, 27(12): 1439-1433.

[6] 淡志强, 薛瑞. 基于改进的包络模型的GBAS完好性评估方法 [J]. 现代导航, 2014(6): 404-409.

[7] PERVAN B, PULLEN S, SAYIM I. Sigma estimation, inflation and monitoring in the LAAS ground system [C]// ION. Proc. ION-GPS 2000. Salt Lake City:ION, 2000.

[8] WEN Hengqing, HAVLICEK Joseph, FAGAN John. B-value research for FAA LAAS station integrity and fault detection [C]// ION. ION NTM 2004. San Diego:ION, 2004.

[9] 赵琳, 武晓雯, 李亮, 等. 基于Hatch滤波法的GPS伪距差分定位分析 [J]. 遥测遥控, 2011, 32(6): 58-62.