对破片飞散参量计算模型的分析和评价
2017-05-03印立魁候秀成赵太勇陈智刚纪刘奇
印立魁, 候秀成, 赵太勇, 陈智刚, 纪刘奇
(1 中北大学地下目标毁伤技术国防重点学科实验室, 太原 030051; 2 西安现代控制技术研究所, 西安 710065)
0 引言
破片的初速和抛射角(也称偏转角)是表征杀伤战斗部破片飞散特性的基本参量,也是设计战斗部和评估战斗部威力的必需参量。相关方面Gurney、Randers-Pehrson、斯坦纽维奇、蒋浩征、冯顺山、周培基等国内外众多学者从不同的角度做过广泛的研究。由于专业书籍相关知识更新较慢,致使诸多有价值的结论和公式依然散布于各文献,难以推广应用,而费时耗力的数值模拟成为当前获取破片飞散参量的主要手段。为充分发挥理论公式快捷、有效的优势,文中针对圆柱战斗部破片侧向飞散参量的计算,系统总结相关公式,并结合试验数据进行分析评价,甄选出精度较高的计算公式,相关公式能推广应用于一般的战斗部结构。
破片抛射角基于破片的初速信息计算,文中先阐述破片初速的计算模型。
1 破片初速模型
战斗部破片初速的影响因素较多,如装药的Gurney常数或爆速、装药形状和结构、壳体破裂半径、装药长径比、起爆方式、破片类型等。相对应的出现了很多形式各异的破片初速模型,从实质上可归纳为计算破片最大速度的基本初速模型和考虑其它因素构建的基本初速修正模型。
1.1 基本初速模型
对等壁厚壳体的柱形装药结构,最经典的破片初速模型有基于能量守恒的Gurney公式[1]:
(1)
还有基于冲量定理的斯坦纽维奇模型[1]:
(2)
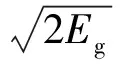
当轴向装药直径或壳体壁厚变化时,需将战斗部轴向分成若干段,用x位置处的β(x)计算对应破片的初速。可将上述初速模型统一为:
v0b=C1(C2+β(x)-1)-1/2
式中:C1和C2表示常数。
1.2 基本初速模型的修正
考虑其它因素构建的初速模型,一般通过修正基本初速模型得到,形如:
v0=kO·C1(C2+(kI·β(x))-1)-1/2
(3)

1.2.1 壳体破裂半径
对整体壳体形式,设装药的初始半径为r0,壳体破裂时的半径为r,壳体破裂半径对初速的影响因子为[1]:
(4)
1.2.2 装药长径比K
长径比K对破片初速的影响,基于文献[3]的试验数据,拟合得到如下修正系数:
kOK=(1+0.115 6K)-1,K>0.5
(5)
对K更小的情况,宜用冲量法得到的公式[5]求解,即
(6)
式中:A为起爆方式的影响系数,取一端起爆另一端有底时为1,中间起爆两端开口为1/2。
1.2.3 破片类型
该因素对初速的影响当前研究尚不系统,一般认为因爆炸产物较早泄露,在相同的装填条件下,预制破片初速为0.8~0.9倍整体或半预制壳体的破片初速[5]。表1为破片类型初速修正系数的取值。
印立魁等[6]的研究表明,该修正系数与装填比呈正相关,与破片密度呈反相关,受装药类型的影响较小;Kim等[7]认为kIf较kOf更适于表征这种影响效果。

表1 破片种类的kOf的近似取值
1.2.4 空心装药结构
对装药中心为空穴和可压缩惰性填料的两种情况,修正系数[10-11]分别为:
kOHa=(1+αβ-1)-1/2
(7)
(8)
式(7)和式(8)中α=φ/ψ(见图1),γ为装药爆炸产物的多方指数。

图1 空心装药结构示意图
1.3 破片初速的分布模型
1.3.1 破片初速值的周向分布
王马法等[12]对单点偏心起爆时破片初速值沿周向的分布建立了模型,其修正系数为:
(9)
式中:k=0.9β2-0.23β+0.14,β∈(0.3,0.9),a、θ分别是表征起爆点偏心距和破片周向分布位置的量(见图2,其中O′为偏心起爆点,n为壳体微元的法线方向,v为破片初速,D为爆轰波在壳体微元处的速度)。

图2 单点偏心起爆下的破片初速
式(9)表明,定向区破片的速度增益与偏心距|OO′|呈正相关。王力等[13]的理论研究表明,双点偏心起爆使定向区破片的速度增益可达30%,但基本不增加定向区的破片密度。
1.3.2 破片初速值的轴向分布
常用的相关模型有3种:冲量模型、Randers-Pehrson等效装药模型和冯顺山公式。针对战斗部最常用的一端起爆形式分别介绍如下:
1)冲量模型
用α∈[0,1]表示破片在战斗部轴向的相对位置。则初速沿轴向分布的修正系数为α处壳体受爆轰产物作用的比冲量iα与壳体内表面所受的最大比冲量iM=max(iα)的比值。iα可由文献[11]中炸药爆炸对刚性壳体侧壁的比冲量近似表示,可得到:
(10)
张寿齐[14]的研究表明上式偏差较大,应更改为:
kOα=(iα/iM)n
(11)
式中,n取值因不同的结构而异,对一端起爆的情况,战斗部有端盖取为0.3,否则取为0.4。
上两式显示α=0.63时破片初速最大。
2)Randers-Pehrson等效装药模型
Randers-Pehrson[15]提出在装药两端分别挖去一个锥体,其中起爆端锥体高度等于装药直径,非起爆端锥体高度等于装药半径,其修正系数为:
kIα=1-(1-min(Kα,1,2K(1-α)))2,K≤2
(12)
该式显示α=2/3时破片初速最大。
3)冯顺山公式
冯顺山等[8,16]由两端敞口的整体壳体爆炸膨胀的X光摄影数据拟合出公式,其修正系数为:
kOx=(1-Ae-Bx/d(x))(1-Ce-F(L-x)/d(x)),K≥2
(13)
式中:x为破片距起爆端的距离;L为战斗部长度;d(x)为x位置处装药直径;常数取值为A=0.361 5,B=1.111,C=0.192 5,F=3.03。
对经典的圆柱战斗部α=x/(2Kr0),式(13)可化为:
kOx=(1-Ae-BKα)(1-Ce-FK(1-α))
(14)
如表2所示,该式中破片初速极值对应的αmax值与长径比K呈正相关。
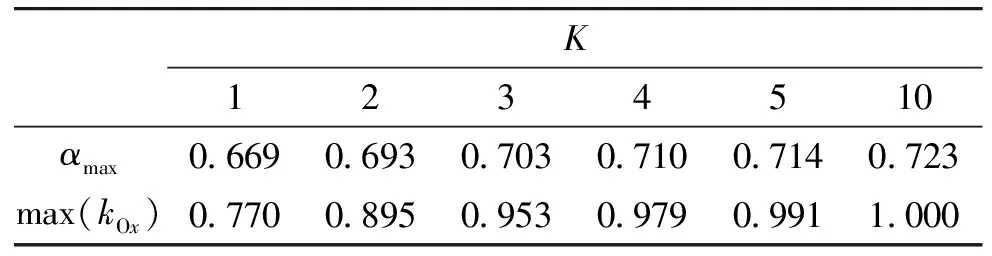
表2 不同K时式(14)的极值及对应的α取值
在K≥2时,式(13)~式(14)的最大值max(kOx)均低于其应达到的值1,即式(13)~式(14)的计算值偏低。
图3(a)~图3(b)的上图给出式(11)~式(12)、式(14)的计算值与文献[9,17]试验值的比较,可见式(11)对初速的整体趋势表征最好,式(14)次之,式(12)最差,三式对实验数据的相关系数依次为0.750,0.726和0.731。
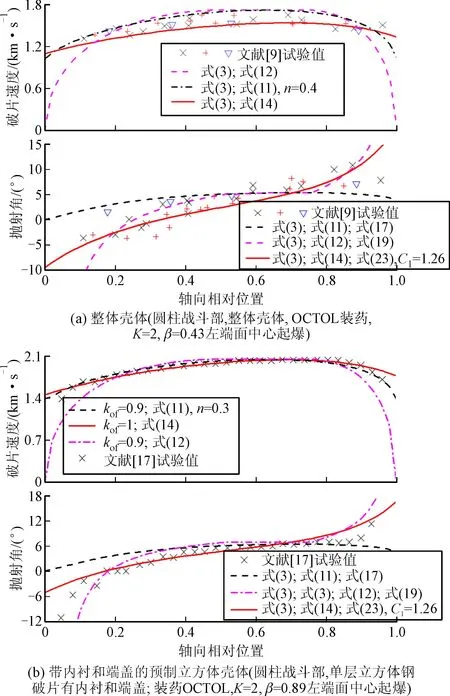
图3 破片初速和抛射角计算值与试验值的比较
2 破片抛射角模型
破片抛射角是破片速度矢量与破片起始位置处壳体法线的夹角。计算破片抛射角的常用模型有Shapiro模型、Randers-Pehrson模型和周培基模型。
2.1 Shapiro公式
Shapiro公式[2]是在Taylor假设和爆轰波从起爆点以球面的形式向外传播的假设下,考虑战斗部壳体外形推导得到的,其形式为:
(15)
式中:γ为壳体法线与中轴线的夹角;φ为作用壳体的爆轰波方向与中轴线的夹角(见图4)。未特别说明,文中角的单位为rad。
由图4可知,破片飞散方向角(速度方向与战斗部中轴线的夹角)为:
λ(x)=γ(x)-δ(x)
(16)
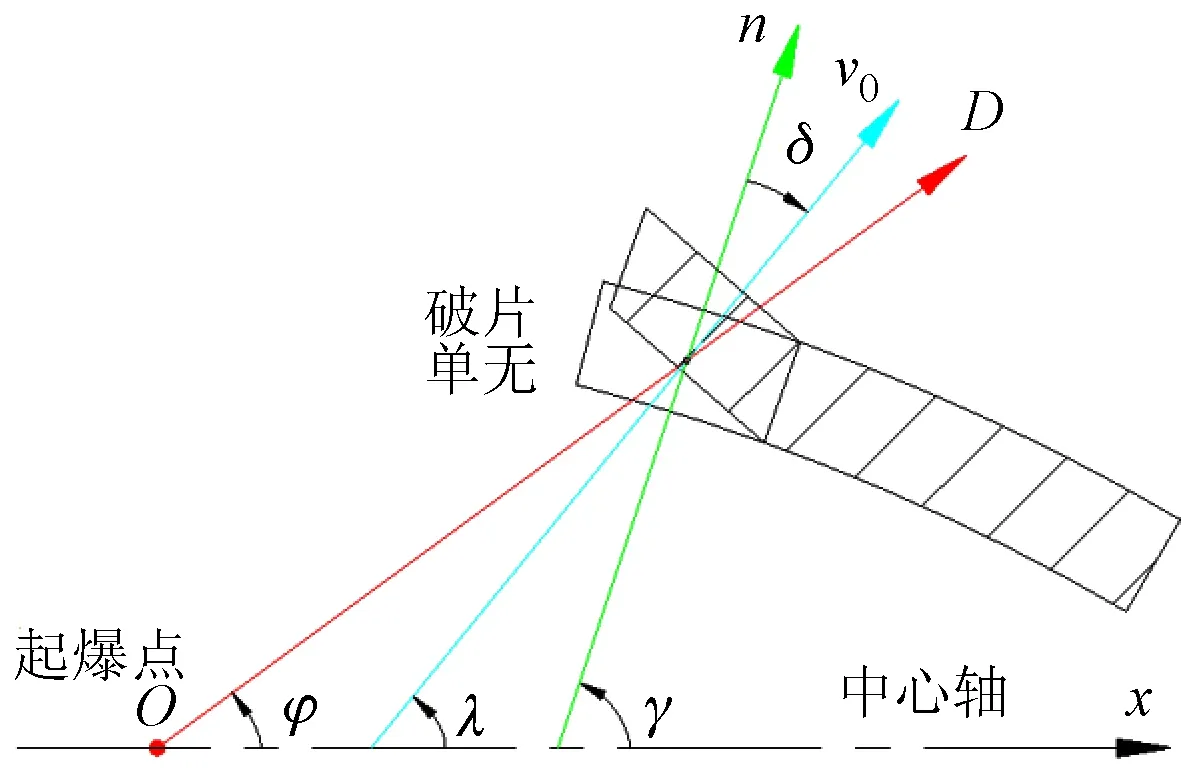
图4 破片抛射角计算说明图
对柱形装药因γ(x)≡π/2,故有:
(17)
由图3(a)、图3(b)的下图可见,式(13)对靠近端部破片的抛射角计算值与实际结果偏差较大,其原因是以Taylor假设为基础的Shapiro公式适用于计算定常条件下的破片抛射角[18],但战斗部端部受稀疏波的影响严重,其爆轰产物的状态是非定常的。
2.2 Randers-Pehrson公式
Randers-Pehrson[17]假设破片的加速形式为:
v(x,t)=v0(x)(1-e-t/τ)
(18)
对应其提出的等效装药初速模型式(12),给出一种精度较高的破片抛射角经验公式:
(19)
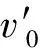
(20)
对于角度δ总有arcsin(δ)>δ;当|δ|<20°时,两者的相对误差不超过2%。故当破片的抛射角不大时,式(19)可简省最后取反正弦的计算,变为:
(21)
同理,式(15)、式(17)也可做类似简化。
2.3 周培基公式
周培基等[18]分析爆轰驱动壳体的变形过程,基于式(18)相同的破片加速形式,推导出破片抛射角的一般计算式:
(22)
式(22)说明,破片抛射角受初速、初速空间梯度、破片加速时间常数和时间常数梯度4个量共同影响,即破片初速的空间和时间分布均影响抛射角。另外,该式与式(21)的前两项完全相同;两式计算结果差异不大[18]。
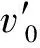
(23)
式中:C1=0.3,但由初速模型得到的v0′(x)/v0(x)值与实际值总有出入,C1值应作相应改变。若用形式相对简单的式(14)计算式(23)中的初速,有:
(24)
当K=1和2时,由文献[9,17]中的试验数据拟合得C1的取值分别为2.42和1.26。
图3(a)、图(b)的下图给出shapiro公式、Randers-Pehrson公式、改进的周培基公式计算值和试验数据的对比,可见式(23)的计算结果相对更准确,式(13)和式(23)结合使用可满足计算破片飞散参量的工程需要。
3 结论
针对破片飞散参量的计算,结合相关文献的试验数据,文中从破片初速和破片抛射角两方面对相关模型进行了系统总结、分析和验证,主要结论有:
1)破片初速轴向分布模型中,修正的冲量模型和冯顺山公式的描述效果较好,不推荐使用Randers-Pehrson模型。
2)破片抛射角模型中,Shapiro公式对端部破片的计算精度较差;一般情况下破片抛射角小于20°,Shapiro公式和Randers-Pehrson公式能简省其最后取反正弦的计算。
3)破片初速的空间分布和时间分布均会影响抛射角的大小。
4)构建了与冯顺山初速公式配套使用的抛射角计算模型,经与试验数据比较,该模型的计算精度高于Shapiro公式和Randers-Pehrson公式。
参考文献:
[1] 北京工业学院八系《爆炸及其作用》编写组. 爆炸及其作用: 下册 [M]. 北京: 国防工业出版社, 1979: 23-34.
[2] 印立魁, 蒋建伟, 门建兵, 等. 立方体预制破片初速计算模型 [J]. 兵工学报, 2014, 35(12): 1967-1971.
[3] 隋树元, 王树山. 终点效应学 [M]. 北京: 国防工业出版社, 2000: 86.
[4] 张国伟. 终点效应及其应用技术 [M]. 北京: 国防工业出版社, 2006: 147.
[5] 周申生. 中高空防空导弹的战斗部 [J]. 现代防御技术, 1987(3): 5-12.
[6] 印立魁, 蒋建伟, 门建兵, 等. 预制破片战斗部破片初速计算模型 [J]. 弹箭与制导学报, 2014, 34(增刊): 258-262.
[7] KIM H S, ROTTENKOLBER E, HARTMANN T, et al. Modifications of the gurney equation to account for gas leakage [C]// National Defence Research Establishment. 28th International Symposium on Ballistics. Atlanta:[s.n.], 2014.
[8] 蒋建伟, 冯顺山, 何顺录. 一种用于评价和计算杀伤威力的数学模型 [J]. 北京理工大学学报, 1992, 12(2): 90-96.
[9] CHARRON Y J. Estimation of velocity distribution of fragmenting warheads using a modified gurney method:ADA 074 759 [R]. [S.l.]: Wright-Puttersonafb of School of Engineering, 1979.
[10] U. S. Naval weapons evaluation facility. Initial fragment velocities from hollow warheads:NR 8282[R]. [S.l.:s.n.], 1964.
[12] WANG Mafa, LU Fangyun, LI Xiangyu, et al. A formula for calculating the velocities of fragments from velocity enhanced warhead [J]. Propellants, Explosives, Pyrotechnics, 2013, 38(2): 232-237.
[13] 王力, 韩峰, 陈放, 等. 偏心对称起爆战斗部破片初速的增益 [J]. 爆炸与冲击, 2016, 36(1): 69-74.
[14] 张寿齐. 圆柱形有壳装药侧向飞散速度分布的预估 [J]. 爆炸与冲击, 1988, 8(3): 215-221.
[15] Randers-Pehrson G. An improved equation for calculating fragment projection angle [C]// National Defence Research Establishment. 2nd International Symposium on Ballistics. Florida:[s.n.], 1977.
[16] HUANG Guanyan, WEI Li, FENG Shunshan. Axial distribution of Fragment Velocities from cylindrical casing under explosive loading [J]. International Journal of Impact Engineering, 2015,76: 2027-2032.
[17] WILLIAM W P, WALTER G S, CHARLES E A. Missile warhead modeling: computations and experiments:ADA 047 294[R]. [S.l.:s.n.]. 1977.
[18] CHOU. P C, CARLEONE J, FLIS W J, et al. Improved formulas for velocity, acceleration, and projection angle of explosively driven liners [J]. Propellants, Explosives, Pyrotechnics, 1983: 8(6):175-183.
