基于量测分配的SMC-PHD改进算法

樊鹏飞, 李鸿艳, 王 雪

(空军工程大学信息与导航学院, 西安 710077)

0 引言

随着有限随机集的提出,概率假设密度(probability hypothesis density,PHD)滤波算法开始逐渐用于解决多传感器多目标跟踪问题[1-3]。PHD的一个显著优点是把多传感器多目标问题看作单传感器单目标处理,避免了数据关联计算,大大降低计算量,实现简单。文献[4-5]利用序列蒙特卡罗(SMC)思想给出了PHD滤波器的SMC实现,即序贯蒙特卡罗概率假设密度(sequence Monte Carlo probability hypothesis density,SMC-PHD)滤波。

通常,为了确保滤波效果,SMC-PHD算法需要大量粒子才能达到一个较高的估计精度,这就导致了耗时长和效率低等问题[6-7]。在迭代中,最耗时的步骤是SMC-PHD的更新。并且目标的数目增多,运算量和计算的复杂度也随之增大,估计精度也会明显下降。另外,对于不同类型的目标(如存活目标、新生目标等)使用同样的全部量测数据集进行目标状态更新,加大了与目标无关的量测(如杂波或其他无关目标的量测干扰等)对目标状态更新的影响,导致目标估计精度随之下降,且估计性能对杂波较敏感,密集目标的情况下这些问题将更加凸显。

为了解决粒子概率假设密度滤波在更新中存在的这些问题,许多学者提出了行之有效的改进方法。文献[8]基于最近邻的思想,提出了一种sigma门限策略,仅仅使用最近的量测值更新粒子。文献[9]中基于量测信息的目标PHD分解思想,提出了一种新生目标强度未知的门限粒子PHD滤波器。文献[10-11]基于簇的思想,在粒子PHD一步预测之后,结合Mean-Shift算法将粒子划分为多个簇,每个簇代表一个目标的状态分布,通过对每个簇中粒子使用簇中的量测集进行粒子的更新,减少计算复杂度。文中基于量测分配的思想,提出了一种在现有序列蒙特卡罗概率假设密度滤波算法基础上的SMC-PHD改进算法,并给出了其实现方法。

1 序列蒙特卡罗概率假设密度滤波算法

设状态空间Es上的状态RFS为X,它的一阶矩(PHD)是Es上的非负函数v(·),对于任何S⊆Es,PHD的集值积分可表示为：

(1)

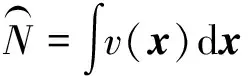
SMC-PHD滤波器的基本思想是在滤波过程中迭代用来表示后验强度的权值和粒子集合,其迭代过程包括预测步和更新步[4-5]。

1.1 预测步骤

假设给定k-1时刻的后验强度vk-1(x),即

(2)

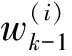
假设k时刻新生目标的随机有限集的PHD为γk,则预测的强度vk|k-1(x)可表示为:

(3)

式中Lγ,k为新生目标的预测粒子数。

(4)

(5)

(6)

(7)

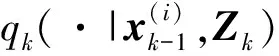
1.2 更新步骤

假设给定k时刻的预测强度vk|k-1(x),即:

(8)

在得到新的量测值集合Zk后,更新粒子的权值进而估计PHD函数vk,则更新的强度vk(x)可表示为:

(9)

式中:

(10)

(11)

(12)

其中：gk(·|·)表示k时刻目标的似然函数;κk(z)=λkck(z)表示杂波强度；ck(z)表示杂波概率密度；每个时刻杂波个数服从参数为λk的Poisson分布;pD,k表示传感器检测概率。

1.3 重采样

和标准SMC滤波算法类似,SMC-PHD滤波器同样存在粒子退化问题,为了降低退化问题的影响,需要对粒子进行重采样。

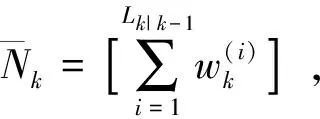
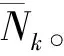
1.4 多目标状态提取

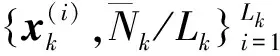
2 改进的SMC-PHD更新算法

传统SMC-PHD滤波器将已有目标和新生目标的强度在预测步后就进行合并,如式(3)所示,式(10)中使用同样的全部量测数据集进行目标状态更新,增大了与目标无关的量测对目标状态更新的影响,导致滤波效率不高、目标估计性能下降[12]。

传统SMC-PHD算法假设新生目标先验已知(如新生目标强度在某些预先指定区域内均匀分布),而更新步骤却利用全部量测数据对新生目标状态进行更新,使得大部分量测数据并不能反映出新生目标,增大了虚警;对于存活目标,使用全部量测数据进行更新使得整个量测空间中的杂波都参与更新计算,导致已有目标估计精度性能下降,特别是在目标密集和高杂波的情况下,估计的性能下降特别明显。针对上述问题,文中提出一种结合最新量测信息,将目标分为存活目标和新生目标分别同时处理(它生目标的情况当作新生目标情况处理),将量测数据最优分配给已有目标和新生目标,再对两类目标分别进行更新计算,降低量测集对目标更新时的盲目性,同时减少量测中的杂波成分,提高了算法估计性能。

2.1 粒子分配

假设给定k时刻的预测强度vk|k-1(x),在得到新的量测值集合Zk后,更新的强度vk(x)可表示为:[12]

vk(x)=vk,b(x)+vk,p(x)

(13)

式中:vk,b(x)为新生目标PHD函数,vk,p(x)为存活目标PHD函数。由于新生目标除采样不同,其他步骤与存活粒子相似,因此为简化算法,这里只介绍存活粒子的分配。

在耕地缓冲100 m范围内农村居民点面积与数量最多，分别占比83.5%和71.5%，且景观形态指数远大于其他区域，原因是区域内农村居民点布局受耕地分割严重，导致离散程度较高。距耕地200 m以外区域，农村居民点斑块所占景观比例仅有0.3%，且斑块密度与景观形态指数均最低，表明耕地对其分布影响大。平均斑块面积与标准差各区域相差不大，则耕地对农村居民点规模影响不大。形状指数在100 m～200 m区域内最大，此区域农村居民点建设既少受到耕地布局的限制，又不会因距离耕地较远而丢失部分生产生活功能，因此形状更为复杂。

对量测集中的每一个量测,需要结合最新量测集中的各个量测信息与目标粒子的单步预测状态的似然值,计算量测-粒子对的匹配概率,并在此基础上分配预测的粒子集。计算匹配概率:

(14)

式中：pij表示k时刻第i个粒子与第j个量测的匹配程度。特别的,当j=0时,表示粒子没有量测与之匹配,代表漏检。

(15)

在式(14)和式(15)的基础上,对粒子进行量测的分配。计算:

(16)

式中mk为k时刻量测集的个数。

现在根据概率将量测分配给相对应的粒子。注意:①可能出现量测没有粒子与之匹配的情况p0(j),此时量测很有可能是由杂波(虚警)引起的,因此其概率p0(j)=0,这在一定程度上能减少杂波的影响。②漏检是造成粒子退化的一个重要因素,这里为pi(0)设置一个门限,这个门限既可以缓解粒子退化,也可以防止未被检测到的目标被忽略掉。文中的门限策略参考文献[13]。③这里的量测和粒子不是根据概率大小一一对应的,存活目标或杂波可能与同一粒子配对,同样粒子根据门限(threshold)也可能与多个量测配对,这与数据关联中目标、量测的一一对应是不一样的。

2.2 粒子更新

对传统SMC-PHD的更新步骤进行改进。

在给定k时刻的存活目标的预测强度vk|k-1,p(x),即:

(17)

在得到新的量测值集合Zk后,更新粒子的权值进而估计PHD函数vk,p,则更新的强度vk,p(x)可表示为:

(18)

(19)

3 仿真实验

验证文中算法,共有3个目标,存在时间分别为1～35 s、5～40 s、12～40 s,初始状态分别为[100.4,2.6,100.1,3]T、[99,3,99.7,2]T、[99.5,2,100.1,4]T,采样周期T=1 s,仿真40步,目标状态向量为xk,目标运动方程为:

xk=Fxk-1+Γωk

(20)

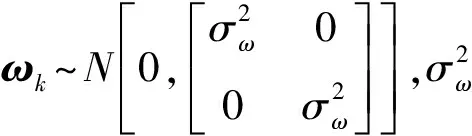
传感器位置为坐标原点,量测方程为:

(21)

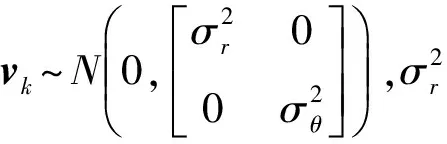
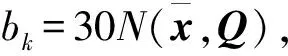
图1是目标运动轨迹图和估计结果图;图2是文中改进算法与传统SMC-PHD在100次蒙特卡罗仿真的平均OSPA距离对比;图3是算法的100次蒙特卡罗仿真中估计的目标个数平均值与真实目标个数的对比。

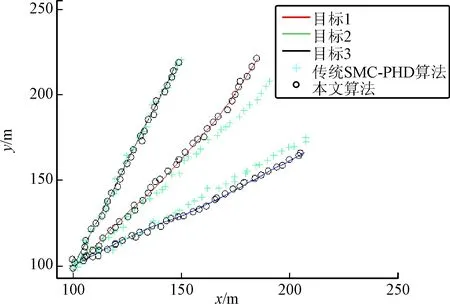
图1 目标运动轨迹和估计结果

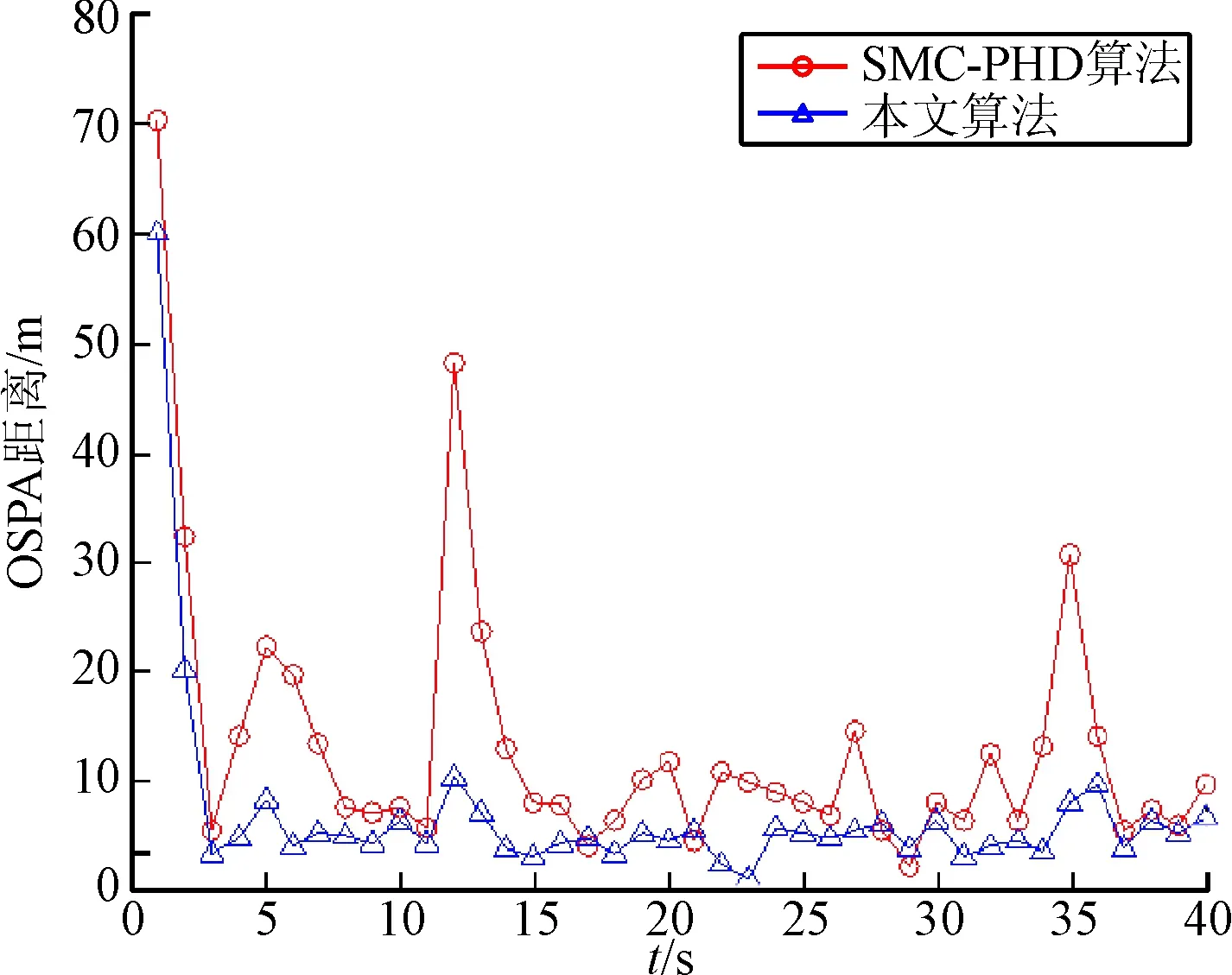
图2 平均OSPA距离对比(λk=30

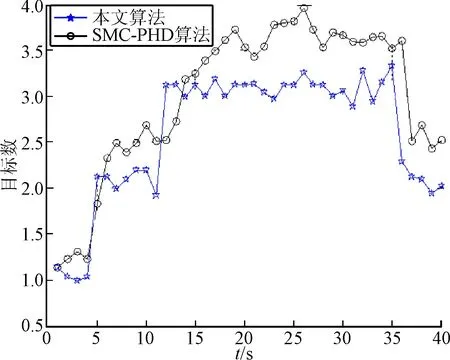
图3 目标个数估计

由图2可以看出,在100次蒙特卡罗仿真中,平均OSPA距离显著增加,文中的改进算法的平均距离在[0,10]区间内抖动,比较稳定,特别是c=30并且3个目标同时存在的时间段,文中改进算法的平均OSPA距离明显低于传统的SMC-PHD,跟踪性能有明显提高。从图3可以看出,文中算法的目标估计个数与真实目标个数非常接近,这从另一个方面证实了文中算法的优越性。

4 结论

文中提出的基于量测分配的SMC-PHD改进算法结合最新量测集中的各个量测信息与目标粒子的单步预测状态的似然值,以概率选取量测值,合理的对粒子PHD算法的更新步骤进行改进,显著增强了粒子PHD滤波算法的鲁棒性,提高了估计精度。

参考文献:

[1] MAHLER R P S. Multitarget Bayes filtering via first-order multi-target moments [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.

[2] MAHLER R P S, Mahler. PHD filters of higher order in target number [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1523-1543.

[3] VO Ba-Tuong, VO Ba-Ngu, ANTONIO Comtoni，et al. The cardinality balanced multi-target multi-bernoulli filter and its implementations [J]. IEEE Transactions on Signal Processing, 2009, 57(2): 409-423.

[4] VO Ba-Ngu, SINGH S，DOUCET A, et al. Sequential Monte Carlo methods for multitarget filtering with random finite sets [J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245.

[5] VO Ba-Ngu, SINGH S, DOUCET A. Random finite sets and sequential Monte Carlo methods in multi-target tracking [C]// IEEE. 2003 Proceedings of the International Conference on Radar. [S.l.]:IEEE, 2003: 486-491.

[6] QUANG Pham Tran Anh, KIM Dong-Sung. Enhancing real-time delivery of gradient routing for industrial wireless sensor networks [J]. IEEE Transactions on Industrial Informatics, 2012, 8(1): 61-68.

[7] MEISSNER D, REUTER S, STRIGEL E, et al. Intersection-based road user tracking using a classifying multiple-model PHD filter [J]. IEEE Intelligent Transportation Systems Magazine, 2014, 6(2): 21-33.

[8] LI T, SUN S, SATTAR T P. High-speed Sigma-gating SMC-PHD filter[J]. Signal Processing, 2013, 93(9): 2586-2593.

[9] RISTIC B, CLARK D, VO Ba-Ngu，et al. Adaptive target birth intensity for PHD and CPHD filters [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1656-1668.

[10] SHI Zhiguo, ZHENG Yunmei, BIAN Xiaomeng, et al. Threshold-based resampling for high-speed particle PHD filter [J]. Progress in Electromagnetics Research, 2013, 136: 369-383.

[11] WANG Junjie, ZHAO Lingling, SU Xiaohong, et al. Cluster-based efficient particle PHD filter [C]∥ IEEE. 2015 International Conference on Control, Automation and Information Sciences.[S.l.]:IEEE, 2015: 219-224.

[12] RISTIC B, CLARK D, VO Ba-Ngu, et al. Adaptive target birth intensity for PHD and CPHD filters [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1656-1668.

[13] 徐从安, 刘瑜, 熊伟, 等. 新生目标强度未知的双门限粒子PHD滤波器 [J]. 航空学报, 2015, 36(12): 3957-3969.

[14] CLARK D E, BELL J. Multi-target state estimation and track continuity for the particle PHD filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1441-1453.