多面交会姿态测量方法研究
2017-05-03崔铁成
王 颖, 葛 超, 崔铁成
(中国白城兵器试验中心, 吉林白城 137000)
0 引言
空间目标的姿态角是评定其系统性能的重要技术指标与提高制导精度的重要依据,也是靶场光电测量的重要内容。获得这些参数,对于分析和评价空间目标运动特性,以及进行故障分析与优化系统设计具有重要意义[1]。
目前,经常采用面面交会法获取空间目标的姿态角,但该方法存在两个问题:1)若两台经纬仪所确定的平面重合在一起,即两个平面的夹角为0°或180°,则无法计算姿态,在0°或180°附近时,也会引起很大的误差,甚至于导致计算结果是错误的;2)理论上,若两个平面存在唯一的交线,则该交线必是目标所在的直线,但受经纬仪测角误差、大气折射、判读误差等因素的影响,经纬仪确定的两个平面的交线并不是目标所在的真正位置,采用几何方法来确定目标所在的直线,存在一定的模型误差。在姿态测量过程中,可以利用图像处理方法提取目标的中轴线,以减少判读误差在姿态测量中的影响,但在目标飞行过程中,由于目标位置和姿态是不断变化的,无法保证两个平面的夹角始终在较好的范围内。针对上述情况,文中提出基于非线性最小二乘法的多面交会测量方法,通过利用多台经纬仪的测量数据进行交会测量,既可减少因面与面夹角较小所带来的计算误差,也可有效利用多台经纬仪的测量数据。
1 多面交会法
1.1 基本原理
若空间有一条直线S,投影到多台光电经纬仪传感器的像面上,成像分别为S1,S2,…,Sk。根据针孔成像模型和中心投影原理,站址O1与S1组成的平面π1,站址O2与S2组成的平面π2…,站址Ok与Sk组成的平面πk,它们的交线即为空间直线S,如图1。
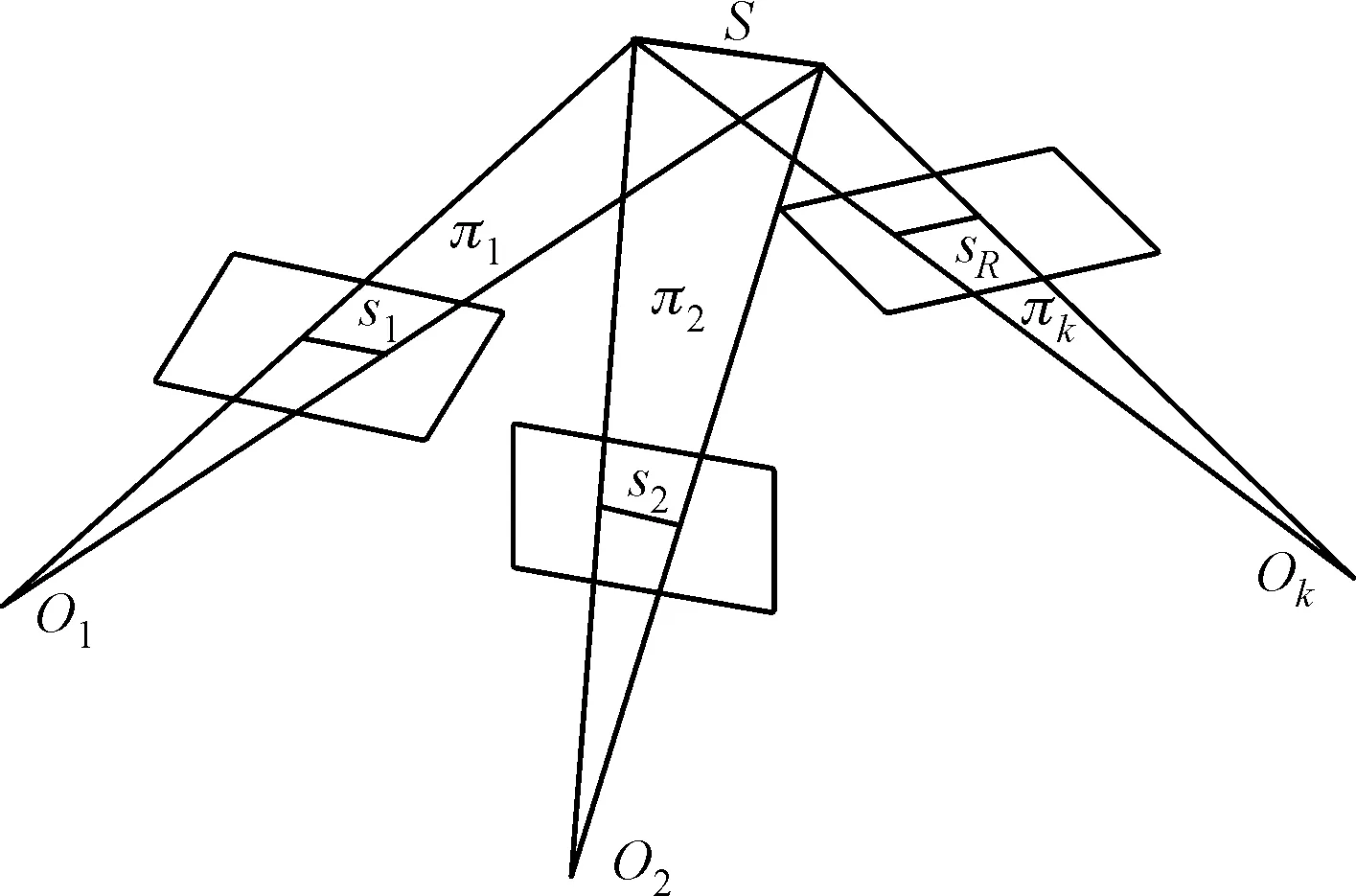
图1 多面交会模型
1.2 数学模型
通过判读可获得目标中轴线在像面上的方程:
aiX+biY+1=0,i=1,2,…,k
(1)
中轴线的提取是目标姿态测量的关键一步,它的精度直接影响姿态测量的精度。关于中轴线的提取不是文中所要研究的主要内容,不做详述。
利用测站坐标、测角信息及式(1)建立平面πi的方程[2]:
Aix+Biy+Ciz+Di=0,i=1,2,…,k
(2)
式中:Ai=fi(air11+bir21)+r31;Bi=fi(air12+bir22)+r32;Ci=fi(air13+bir23)+r33;Di=fi(aitx+bity)+tz;fi为经纬仪Oi的焦距;rij为像机转换矩阵参数,i,j=1,2,…,k;tx、ty、tz为平移参数。
方程(2)的建立,有兴趣的读者可参看文献[2]。
定义正交矩阵:
RLB=RZ(90°-L)RX(-B)RY(90°)=

(3)
式中:L、B为相应站址的大地经度、大地纬度。
由式(2)可知,在测站坐标系下,经纬仪所确定平面πi的法向矢量(Ai,Bi,Ci,通过如下的坐标变换公式:
(4)

将(Abi,Bbi,Cbi)单位化,得到平面πi在参考坐标系下的单位向量(li,mi,ni):
(5)
理论上,空间目标在每台经纬仪所确定的平面π内,则目标所在的直线即为平面π1,π2,…,πk唯一的交线,对每个平面πi而言,其法线垂直该平面的任何一条直线,必然也垂直于目标所在的直线,因此,k个平面的法线同时垂直于目标所在的直线。设目标所在直线的方向向量为(l,m,n),则存在如下关系:
(li,mi,ni)·(l,m,n)=0,i=1,2,…,k
(6)
但在实际应用中,由于大气折射、测量误差、判读误差等因素的影响,平面π1,π2,…,πk不可能相交于一条直线,而(li,mi,ni)与(l,m,n)的夹角为π/2+θi,θi=arccos(lil+mim+nin)-π/2,i=1,2,…,k,在0附近的较小邻域内。
令:
(7)
采用非线性最小二乘法[3-4]进行估计,使式(7)最小的向量为(l,m,n),即为目标所在直线方向矢量的最小二乘估计,有了该矢量,则可计算目标的偏航角φ和俯仰角φ:
(8)
(9)
1.3 L-M迭代求解
由于式(7)中θi是非线性的,文中采用Levenberg-Marquard迭代法(简称L-M迭代法)求解(l,m,n)的估计。令:
θ=(θ1,θ2,…,θk)T,M=(l,m,n)
则式(7)可简化为:
F=θTθ
(10)
定义θ的雅克比矩阵:

L-M迭代法具体算法如下:
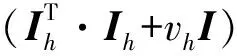
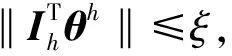
得到偏差量δh;
③令Mh+1=Ih+δh,并计算:
④若rh<0.25,则令vh+1=4vh,否则,如果vh+1=vh/2,否则令vh+1=vh;
⑤令h=h+1,转到②。
通过L-M迭代法获得的Mh即为所求,代入式(8)、式(9)可获得空间目标的姿态角。
2 试验验证
为了验证文中提出的多面姿态测量方法,选用3台光电经纬仪,利用可见光测量电视分别从不同角度瞄准一台光电经纬仪的光学镜筒,并采集可见光视频图像,通过判读获得镜筒在靶面上的中轴线方程,分别利用面面交会法和多面交会法得到镜筒的偏航角和俯仰角,并计算偏航角和俯仰角的均值和标准差,经纬仪布站如图2所示。
部分计算结果如表1。其中,由于1#、3#两站确定的面面交会角在0°附近,其计算的偏航角和俯仰角是错误的,1#、4#两站确定的面面交会角最好,其计算结果的标准差最小。将1#4#、3#4#、1#3#4#偏航角和俯仰角的比对结果进行绘图。从图4~图5来看,多面交会法计算结果的标准差要小于面面交会法计算结果的标准差,由此得出,多面交会法计算的精度更好。
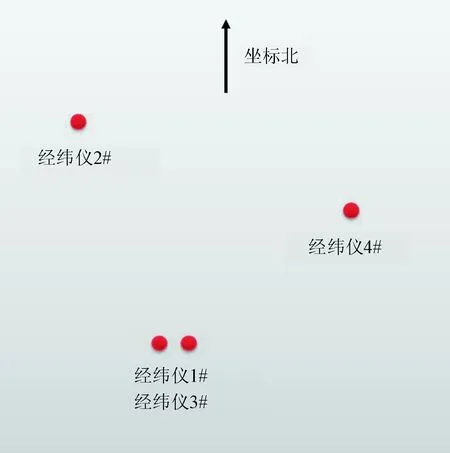
图2 光电经纬仪布站图

图3 光电经纬仪判读示意图
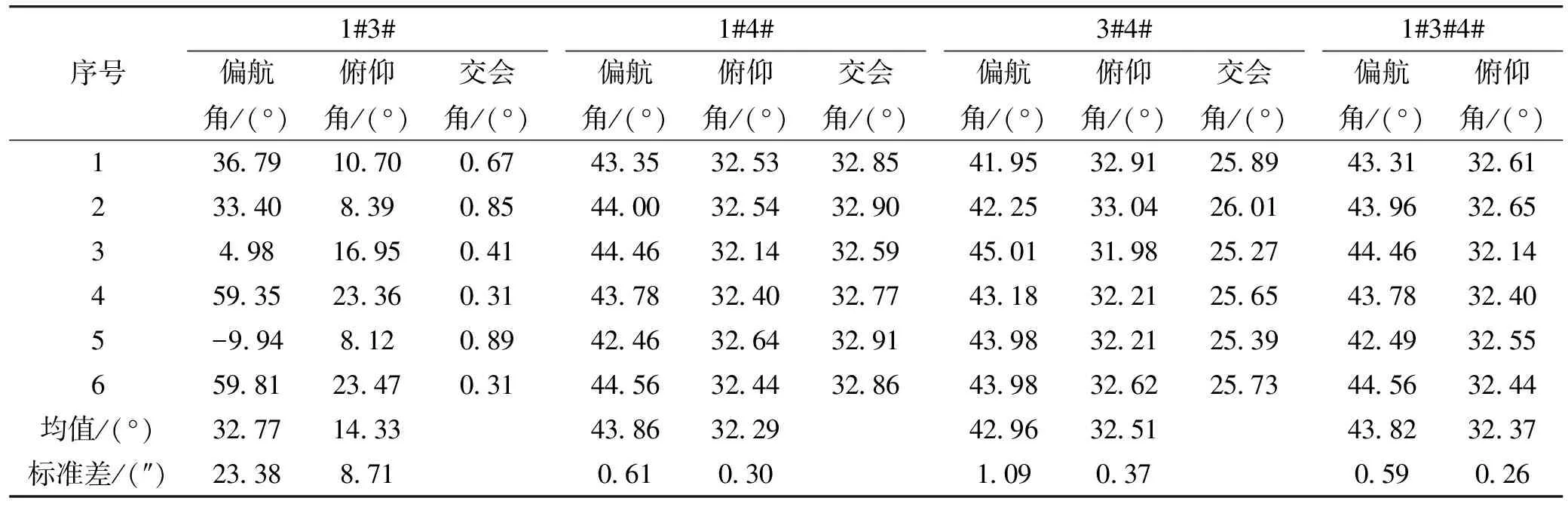
表1 姿态计算结果表

图4 3种偏航角计算结果比对图
图5 3种俯仰角计算结果比对图
3 结论
文中提出的基于非线性最小二乘法的多面交会姿态测量法,采用多台光学经纬仪的测量数据进行交会计算,不仅有效利用了多台光测设备的冗余数据,而且避免了目标在飞行过程中面面交会角较小时造成的误差,甚至是错误的,该方法易于实现,将其应用到数据处理姿态测量中,具有重要的实际意义。
参考文献:
[1] 崔彦平. 运动目标姿态与速度测量的理论及实验研究 [D]. 天津: 天津大学精密仪器与光电子工程学院, 2006: 1-8.
[2] 于起峰, 尚洋. 摄像测量学原理与应用研究 [M]: 北京: 科学出版社, 2009: 31-47.
[3] 李明奎. 非线性模型空间测量数据处理理论及其应用 [M]. 北京: 化学工业出版社, 2013: 14-27.
[4] 刘利生. 外弹道测量数据处理 [M]. 北京: 国防工业出版社, 2002: 16-21.
