下挂式空中发射运载火箭的动网格仿真分析

舒 杰, 张登成, 张艳华

(空军工程大学航空航天工程学院, 西安 710038)

0 引言

空中发射方式同传统的发射相比在军事效能和经济效益方面具有明显的优势。空中发射方式灵活,不受空间和时间的限制,提高了导弹的突防能力与生存能力;空中发射的分离初始高度可以将有效载荷的入轨成本降低30%,同时,空中发射载机可重复利用,这都极大提高了发射的经济性。

下挂式空中发射运载火箭是空中发射运载火箭的一种方式,下挂式就是将有效载荷悬挂固定于载机的机翼下或机腹下,发射时启动载机上的连接分离机构,实施对有效载荷的投放。通过对下挂式分离过程的分析与研究,发现分离过程中机箭气动耦合会对分离的安全性产生不确定影响,同时分离后载机与运载火箭的控制率也是基于机箭气动特性设计的。因此,对于机箭气动耦合研究十分重要。

图1 空中发射运载器的发射方式

在国外,由轨道科学公司研制的飞马座运载火箭已进行了多次飞行试验并成功投入了商业化运营。Van Cuong Nguyen[1]等分析了机箭系统发射阶段的鲁棒稳定性;Eric W.M[2-3]等利用实验的方法,研究了重装空投货物出舱后机-物-伞系统的气动耦合特性。目前国内关于下挂式空中发射运载火箭技术的研究较少,主要集中于概念性研究[4],在气动耦合特性研究方面,陶如意[5-7]等应用风动试验和数值方法研究了超音速子母弹分离过程气动耦合作用的流场特性,得到了流动机理;王晓鹏[8]结合数值模拟与导弹运动方程, 研究了导弹发射过程的分离轨迹。

文中基于动网格技术仿真模拟了机箭分离过程,研究了运载火箭与载机分离过程中的轨迹和姿态变化规律,同时分析了载机与运载火箭分离过程中的气动耦合特性。结果表明在一定的条件下,机箭安全分离,并且分离后运载火箭可以达到点火条件。

1 空射过程及问题描述

1.1 下挂式空中发射分离过程

运载火箭由载机携带至12 km的高空,当飞行马赫数达到0.8时,载机与火箭按一定的发射角度进行分离。以投放时刻为零时刻计时,此时火箭与载机分离,火箭沿载机航向斜下方滑翔,在载机脱离危险区域时运载火箭第1级发动机点火。

1.2 分离过程中需要解决的问题

载机与运载火箭分离过程中会产生气动耦合作用,这会对机箭安全分离产生巨大的不确定性。因此,通过动网格仿真分离过程,探索运载火箭与载机分离过程中的轨迹和姿态变化规律,设计分离开始的载机飞行状态状态参数(高度、速度、姿态),确定运载火箭无动力飞行阶段舵面控制规律具有十分重要的意义。

2 计算方法及数学模型

2.1 机箭分离仿真方法

整个机箭分离过程为气动干扰作用下的六自由度运动过程,采用CFD动网格技术对其进行仿真模拟。

仿真流程图如图2所示。

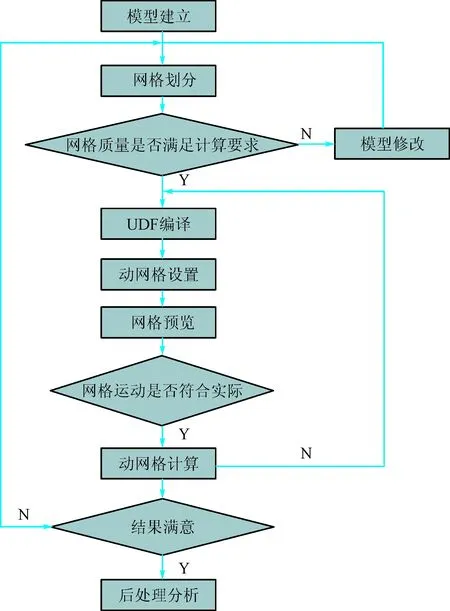
图2 仿真流程图

2.2 六自由度求解器与动网格数学模型

惯性坐标系下质心平移运动的控制方程[9]:

(1)

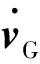
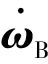
(2)

式中:L为惯量张量;MB为力矩矢量;ωB为刚体的角速度矢量。力矩从惯性坐标系转换到体坐标系:

MB=RMG

其中R为如下的转换矩阵:

(4)

式中:Cx=cosx,Sx=sinx;角度φ、θ、ψ分别代表绕x、y、z轴转动的欧拉角。

速度和角速度通过上面方程(1)和方程(2)计算出来后可以通过数值积分的方法得到物体此时的角度和位移。

弹簧光顺模型中,网格边被理想化为节点间互相连接的弹簧。网格边界节点发生位移后,会产生与位移边界成比例的力,力的大小由胡克定律计算。边界节点产生的力破坏了弹簧系统原有的平衡,但是在外力作用下,弹簧系统会经过调整以达到新的平衡[10]。

根据胡克定律,弹簧力由式(5)计算。

(5)

式中:Δxj与Δxi分别为节点i与j的位移;nj为与节点i相连接的节点数量;kij为节点i与节点j之间的弹簧刚度。刚度由式(6)定义

(6)

式中：kfac为弹簧常数因子(spring constant factor)当处于平衡状态时,与节点i相连的所有弹簧力合力为0。这一条件可以用式(7)进行迭代计算:

(7)

式中：m为迭代次数。当迭代计算结束后,位置更新通过式(8)实现。

(8)

式中:上标n+1与n分别表示下一步时间节点位置与当前时间节点位置。

弹簧常数因子用来控制弹簧刚度。该参数取值范围为0～1。0表示弹簧间没有阻尼,边界位移会对内部节点的运动产生更多的影响,取值越大,边界位移对内部节点影响越小,意味着内部产生变形的网格更多集中于边界附近位置。

对于边界局部小位移的情况,可以采用弹簧光顺的方法进行网格更新,但是如果运动边界位移过大,采用光顺方法可能会导致网格质量下降,甚至出现负网格体积,导致计算终止。为此,引入另一种网格更新方法——网格重构,即将网格畸变率过大或尺寸变化过于剧烈的网格集中在一起进行局部网格重新划分。

在进行局部网格重构之前,首先将需要重新划分的网格识别出来,文中采用的计算软件Fluent主要利用网格畸变率与网格尺寸进行网格识别。在计算过程中,若网格尺寸大于最大尺寸或者小于最小尺寸,或网格畸变率大于设定的畸变值,则网格会被标记为需要重新划分的网格。在遍历所有网格并对网格进行标记之后,开始网格重划分的过程。

3 仿真过程与分析

3.1 模型建立

文中采用国产大型运输机作为载机,为满足空射运载火箭的要求,需对载机做出部分改装。图3为设计的火箭挂架及为便于火箭挂载在机腹尾部开的槽,整个模型运用Soidworks软件建立。

图3 载机与挂架

考虑到下挂式空中发射火箭与载机分离后需在空中无动力飞行一段时间,需有良好的气动外形,火箭利用尾翼和机翼实现了这一要求。如图4,火箭尾部固定有3个尾翼,里面装有3个控制尾翼偏转的伺服作动器和控制电子设备。尾翼包括一个垂直尾翼和两个水平尾翼,水平尾翼的翼展为1.5 m,用于火箭无动力飞行期间的飞行控制。机翼呈三角形,切去了两端翼尖;采用10%的菱形翼型,前缘较钝。机翼翼展为6.7 m,厚度20 mm,可以产生足够大的升力[11]。

图4 运载火箭

3.2 网格划分

文中使用非结构四面体网格生成外流场区域及机箭表面网格,生成网格总数为617万。

图5 自适应网格划分

图6 棱柱层网格

为了精确计算火箭所受到的气动力,在火箭的表面增加了10层棱柱层网格来模拟附面层。

3.3 动网格设置

考虑到机箭分离过程中火箭位移较大,采用弹簧光顺与网格重构方式相结合的方式进行动网格计算。为了使两种动网格更新方式搭配合理,将弹簧常数因子设为0.05。同时设置了尺寸函数使动网格运动过程中网格分布更加均匀合理。

为了使网格计算更加精确,将附面层网格设置同火箭一起运动。首先将火箭表面的棱柱层网格标记起来,然后使用标记的网格将外流场区域分割开来[12],如图7。

图7 被标记的棱柱层网格

火箭的质量及转动惯量等参数都在UDF中设置。设置时间步长0.002 s,共计算2 500步。同时设置了网格运动动画,对动网格运动进行实时监控。

3.4 仿真结果及分析

通过Fluent动网格计算得到分离轨迹图如图8。

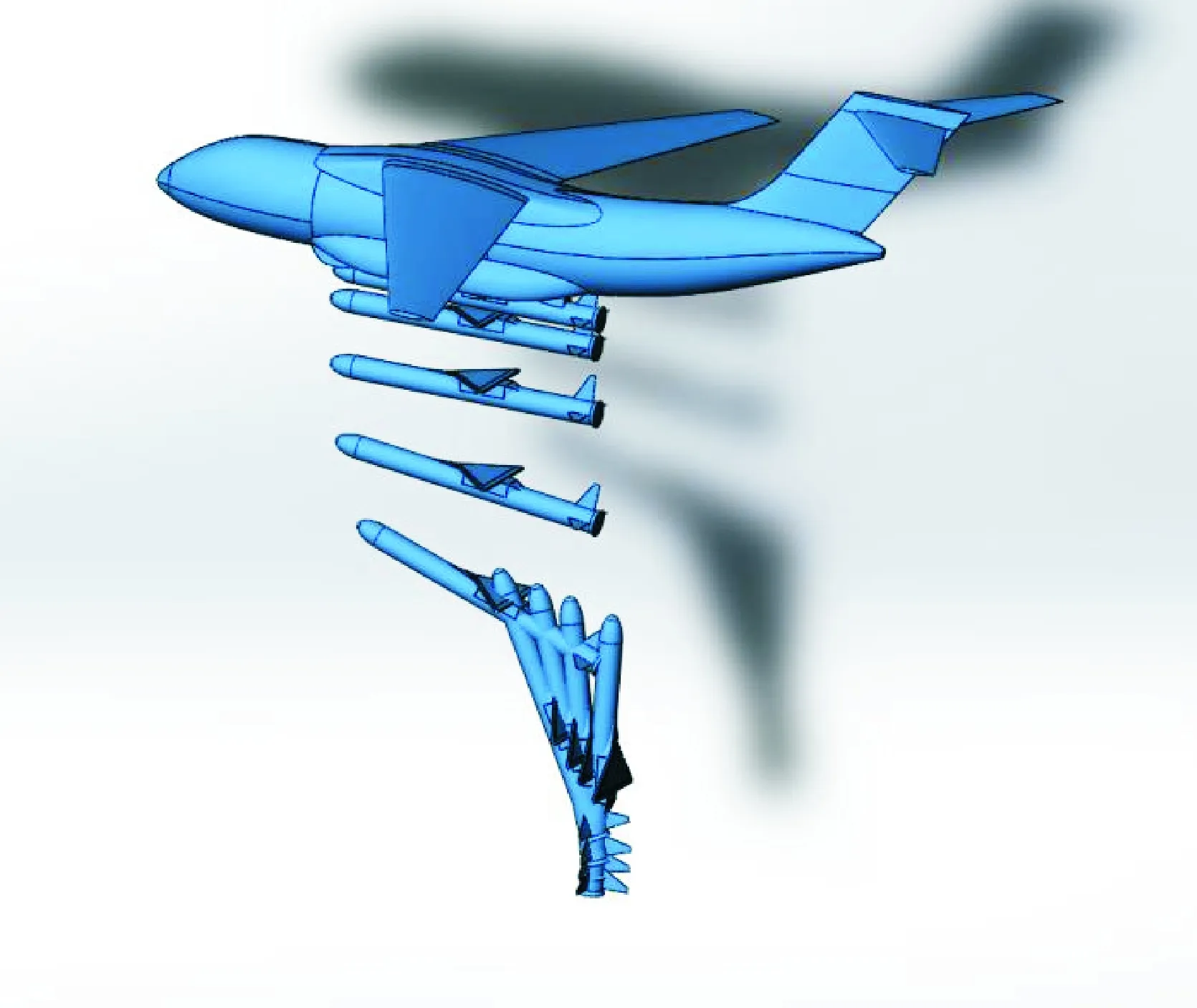
图8 分离轨迹图

下落过程中火箭角度的变化如图9所示。其中横轴为时间,纵轴为火箭俯仰、偏航及滚转角的变化。

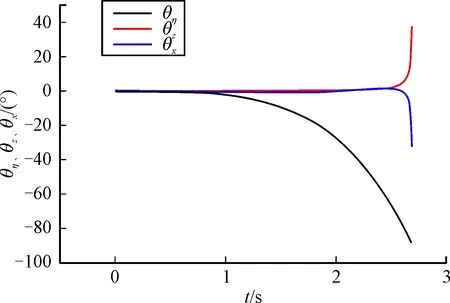
图9 俯仰、偏航及滚转角变化

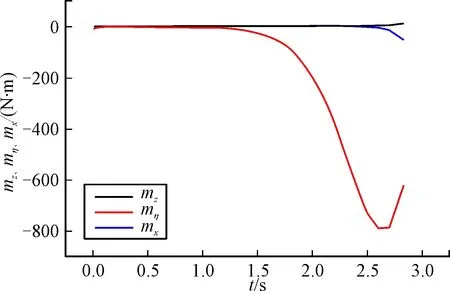
图10 俯仰、滚转及偏航力矩变化

分析图像可知,火箭在2.65 s时达到垂直状态。其后,火箭的滚转角与偏航角发生剧烈变化,滚转与偏航力矩增加,如图12为机翼与尾翼产生的不对称压力云图。因此,要实现火箭在垂直状态下点火,必须设计正确的控制规律,通过火箭的尾翼调整其俯仰、滚转及偏航力矩,以此来实现火箭点火时俯仰、滚转及偏航力矩为零。

图11 有无载机火箭升力系数变化对比

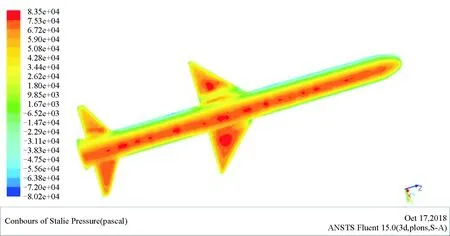
图12 不对称压力云图

图13 机箭气动耦合压力云图

有载机条件下,火箭的升力系数随着迎角增加而增加,在t=2.25 s,θη=-43.27°时,升力系数达到最大。其后,火箭发生剧烈的气动分离,升力系数减小。对比有无载机条件下火箭的升力系数变化可以看出,有载机条件下的火箭升力系数在火箭未发生气流分离失速前是优于无载机条件的,可以减小分离过程中产生的高度损失。这是由于火箭与载机之间气动耦合形成了低压区,导致火箭升力系数增加,如图13所示。

4 结论

文中研究了下挂式空中发射运载火箭机箭分离过程,运用动网格技术对其进行了仿真研究,分析了

运载火箭分离轨迹及机箭气动耦合特性。为下一步优化设计机箭分离状态参数及火箭控制规律奠定了研究基础,同时文中的研究方法具有较高的工程实用价值。

参考文献:

[1] NGUYEN Van Cuong, MARINO Riccarno, DAMN Gilney. Robust stabilization of an airlaunch system after launching phase [C]// IEEE. 51st IEEE Conference on Decision and Control. [S.l.:s.n.], 2012.

[2] ERIC R. ANDREAS S, JANOS A, et al. Coherent wake structures for transport aircraft at cargo airdrop configurations including parachutes[C]∥AIAA. Proc. of 31st AIAA Applied Aerodynamics Conference & Fluid Dynamics and Co-located Conferences. [S.l.:s.n.], 2013-2536.

[3] ROOSENBOOM Eric W M, SCHRODER Andreas, AGOCS Janos, et al. Experimental investigation of the flow field topology for several cargo drop configurations: AIAA 2012-3198 [R]. [S.l.:s.n.]，2012: 2012-3198.

[4] 涂良辉, 杨坤, 王英, 等. 飞行器空基发射运载火箭技术研究 [J]. 教练机, 2014(4): 41-45.

[5] 陶如意, 张丁山, 赵润祥, 等. 超音速子母弹分离干扰流场数值模拟与试验研究 [J]. 空气动力学报, 2010, 28(3): 310-315.

[6] 陶如意, 王福华, 季晓松, 等. 超音速子母弹分离气动干扰风洞试验 [J]. 弹道学报, 2008, 20(4): 24-27.

[7] 陶如意, 吴艳滨, 王浩, 等. 时序抛撒子母弹多体干扰气动特性的数值模拟 [J]. 弹道学报, 2011, 23(3): 53-58.

[8] 王晓鹏. 导弹弹射发射分离轨迹的数值研究 [J]. 弹箭与制导学报, 2012, 32(3): 69-72.

[9] 郑无计, 张登成, 张艳华, 等. 基于动网格对内装式空射火箭分离过程的仿真 [J]. 弹箭与制导学报, 2015, 35(5): 119-122.

[10] 胡坤, 李政北. ANSYS ICEM CFD工程实例详解 [M]. 北京: 人民邮电出版社, 2015: 276-281.

[11] CURRY R E, MENDENHALL M R, MOULTION B. In-flight evaluation of aerodynamic predictions of an air-launched space booster: AIAA 91-5046[R]. [S.l.:s.n.], 1992.

[12] 隋洪涛, 李鹏飞, 马世虎, 等. 精通CFD动网格工程仿真与案例实战 [M]. 北京: 人民邮电出版社, 2013: 66-70.