高空模拟引射器启动特性的实验和数值计算研究

孙顺利, 李 纲

(中国空空导弹研究院, 河南洛阳 471009)

0 引言

引射器作为一种结构简单的流体机械,在航空航天、制冷、化学激光器、工业生产领域应用非常广泛。目前在地面试验中,采用主动和被动两级引射器共同工作来模拟高空中的低压环境,用于研究空空导弹固体火箭发动机在高空环境中的点火和推力特性,而在发动机点火前,引射器的启动特性直接影响整个引射器系统能否开始正常工作。

针对引射器的启动特性,国内外做了大量的实验研究[1-6],实验结果表明引射器的启动过程需要引射器总压达到某一临界值才能启动。随着计算机技术和数值计算方法的不断发展,CFD数值计算方法已经广泛应用于引射器内部流场的研究。徐万武等人[5]对零二次流引射器进行了启动性能数值研究。杨建文等人[7]研究了引射器几何结构和流动参数对启动性能的影响,这些工作只得到部分结果,有助于理解引射器的启动过程,但是没有详细分析造成引射器成功启动和未成功启动状态的内部流场结构差异,更没有对其进行理论分析验证

文中采用实验和数值计算两种方法来研究主动引射器的启动特性,分析启动过程中引射器内部的流场变化,并分析真空舱压力与流动形态之间的关系,得到引射器启动过程的流动机理,并对启动过程中的流动形态变化,采用正激波理论对引射器启动过程中的最小启动压力和最小保持启动状态的压力进行理论计算分析。

1 实验设备和启动过程实验结果

1.1 实验设备和工作原理

图1是固体火箭发动机高空模拟实验系统的示意图,主要包括真空舱、环形喷管主动引射器、中心喷管被动引射器(火箭发动机喷管)、混合室、扩压器和发动机喷管等。火箭发动机喷管射流进入下游直管段内产生被动引射,之后被动引射器气流与下游的环形喷管主动引射器气流在下游混合室内混合,最终通过扩压器排出到大气,其中主动引射器超音速气流需要在发动机喷管工作前将真空舱内的压力抽吸到某一真空度(小于一个大气压)。文中主要研究在没有发动机喷流情况下的主动引射器(图1中的实线部分)的启动特性。

1.2 启动过程实验结果分析

图2是发动机不点火,主动引射器从启动到关闭的整个过程中主动引射器进口总压与舱压的对应关系图。可见启动特性主要表现在三方面:1)主动引射器未启动前,主动引射器压力升高,舱压随之下降;2)当主动引射器总压升高至1 300 kPa或更高时,舱压快速下降至7 kPa左右,主动引射器成功启动;3)主动引射器启动后,主动引射器压力降低,舱压下降,但变化幅度极小,说明引射器启动之后,舱压对主动引射器压力变化不敏感;4)主动引射器关闭阶段,舱压随主动引射器总压减小而逐渐恢复到一个大气压,但路径与启动前的路径不一致。

在主动引射器启动前和启动后,主动引射器总压为1 000 kPa时,舱压对应的两个值分别为45 kPa和7 kPa,二者之间相差38 kPa,这种现象被称为启动迟滞效应,即引射器需要足够高的进口总压才能使得引射器启动成功,之后降低总压,舱压仍然可以保持稳定。

研究造成两种状态之间差异的启动迟滞现象,有助于理解引射器的工作原理和提高对固体火箭发动机高空模拟引射器的启动性能。然而试验系统的内部流场是不可见的,只能得到少量的测量参数,并不足以有效的分析造成两种状态差异的原因,而数值计算方法可以得到主动引射器内部的详细流场结构,为分析这两种状态之间的差异提供了一种有效方法。

2 数值计算方法

文中不考虑发动机喷流的影响,因此将被动引射器、真空舱和发动机喷管移除,只计算主动引射器、混合室和扩压器,同时由于整个高模设备是中心对称的,因此整个计算域可以简化为二维的中心对称模型(如图3所示)。

2.1 计算域和边界条件设置

边界条件包括环形喷管主动引射器进口(pressure-inlet)、扩压器出口(pressure-outlet)、中心轴(axis)和无滑移壁面(wall),扩压器出口通向大气(101.325 kPa),大部分的壁面处的y+<1。

图3 计算域和边界条件

2.2 计算方法设置

求解器设置为采用求解二维稳态的质量、动量、能量输运量的可压缩N-S方程[6],湍流模型采用标准k-ε模型,空间离散方法采用隐式Roe-fds通量,差分格式为二阶迎风格式,流体物性为理想空气气体模型。

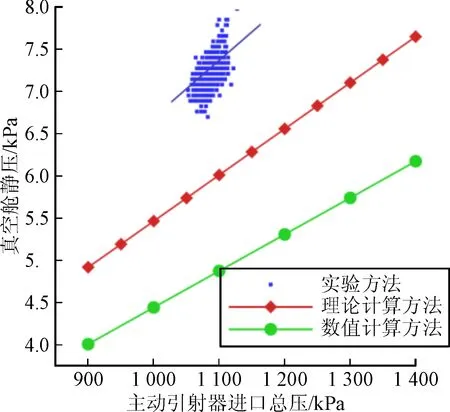
图4 引射器启动后,理论计算、数值计算和实验结果的舱压对比

2.3 计算结果可靠性验证

图4是引射器启动后,理论计算、数值计算和实验的真空舱压力对比图,其中理论计算方法见Fabri在文献[8]中。对比结果显示,三种方法得到的主动引射器总压与舱压的变化规律相同,误差不影响文中的研究目的和在工程实践中的应用,因此,数值计算方法可以用于再现和预测实验结果。

3 数值计算结果分析

3.1 数值计算工况和结果

为了研究主动引射器的启动特性,根据主动引射器启动过程中进口总压的变化规律,数值计算算例主要包括5类工况,分别对应5种流动形态,包括主动引射器从不启动到启动,再到不启动的整个过程。其结果见图5。

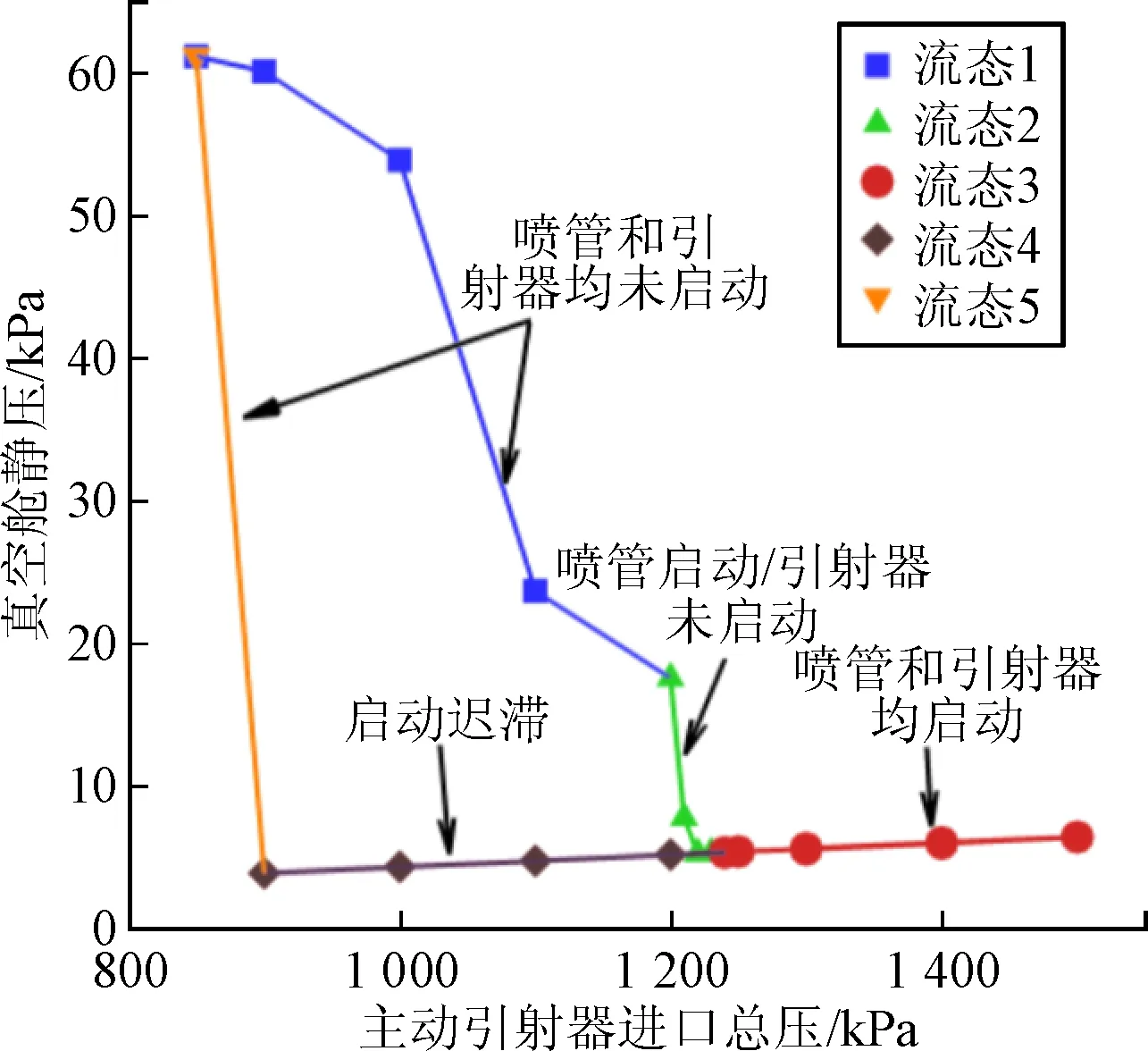
图5 数值计算得到主动引射器进口总压与真空舱静压的关系

与实验结果一样,数值计算结果同样具有启动迟滞现象,即只有当主动引射器的进口总压大于等于1 240 kPa时,引射器可以成功启动。虽然数值计算得到的引射器启动总压(1 240 kPa)比实验值(1 300 kPa)小60 kPa,但考虑到试验过程中存在误差,该计算结果在可接受范围内,因此数值计算方法能够比较准确的模拟引射器的启动过程。

3.2 启动过程中流场变化和迟滞现象原因分析

舱压随主动引射器进口总压变化的结果表明主动引射器从不启动到启动状态之间必然存在一个流动形态转变过程。图6是启动过程中不同主动引射器进口总压下的引射器内流场的人工纹影图。

主动引射器进口总压P0小于1 000 kPa时,在引射器喷管出口扩张段内或出口位置处,存在一道正激波(流态1);P0增加到1 200 kPa时,引射器喷管出口位置处的正激波向下游移动进入混合室(流态2.1),此时喷管启动,超音速射流膨胀程度升高;继续提高P0至1 230 kPa,进入混合室内的超音速射流膨胀程度进一步增强,占据整个混合室流通截面,之后下游形成一道非常强的正激波(流态2.2),将混合室分成两部分,上游为超音速,下游为亚音速,此时真空舱压力已经稳定,但是整个流场形态并不稳定,引射器还不能认为是成功启动。流态2.2相对于流态2.1的正激波的波前马赫数更高,因此需要的波前总压更高。

图6 不同主动引射器进口总压下的引射器内流场的人工纹影图

由于混合室壁面具有收敛带角度,该较强的正激波(流态2.2)会在壁面形成斜激波反射,同时由于上下对称的原因,上下侧的激波也会在中心线处相交碰撞改变方向,之后经过一系列的激波和膨胀波的变化,减速增压,最终在下游二次喉道位置处形成正激波(流态3),由于二次喉道下游为扩张段,存在较强的边界层分离现象,在壁面处形成λ形正激波,之后以激波串的形式变为亚音速。

由于斜激波的减速增压作用和流通截面的收缩影响,流态3的波前马赫数要比流态2.2的波前马赫数低,因此流态3的正激波要比流态2.2的正激波强度弱,再加上混合室内的斜激波的压力损失要比正激波的压力损失小,一旦流态2.2的正激波建立后,上游总压稍微增大一点,该正激波会自发的向下游传播,直至移动到二次喉道位置,形成流态3,之后在亚音速扩压器内,通过一系列的斜激波减速增压排向大气环境。流态3的λ形正激波的波面形状,显著增大的激波的截面,允许通过更多的流量。如果继续增大主动引射器进口总压,该λ形正激波波面会继续增大,该激波位置会向下游移动。如果主动引射器进口总压不断降低,该λ形正激波逐渐向上游收缩,直至在二次喉道内变成一道较弱的平面正激波(流态4)。当引射器进口总压不足以支撑流态4的斜激波和弱正激波的压力损失后,流态4的在二次喉道的弱正激波将会迅速向上游移动,恢复到流态5(与流态1相同)。

通过分析不同引射器进口总压下流场形态的变化,可见引射器启动特性与其内部的流动形态(激波位置)变化直接相关,而启动过程的迟滞现象主要由以下两方面造成:

1)达到流态3必须先达到流态2.2,而流态2.2的总压损失大于流态3,因而流态2.2需要较高的主动引射器进口总压。

2)流态4的总压损失比流态3的压力损失小。

3.3 引射器启动迟滞现象的理论分析

为了在工程应用中更好的利用这种迟滞现象,有必要通过理论公式来预测迟滞现象中的引射器的最小启动压力和最小保持启动状态的工作压力。

3.3.1 引射器最小启动压力理论计算分析

根据图6中的引射器启动过程中激波的变化过程,当主动引射器的进口总压足够大时,环形引射器出口处的激波向下游发展到混合室内形成一道正激波,该正激波完全封闭住混合室截面,此时主动引射器进口总压认为是引射器能够启动的最小启动压力。根据其物理现象和流动机理,可以采用正激波理论计算最小启动压力。

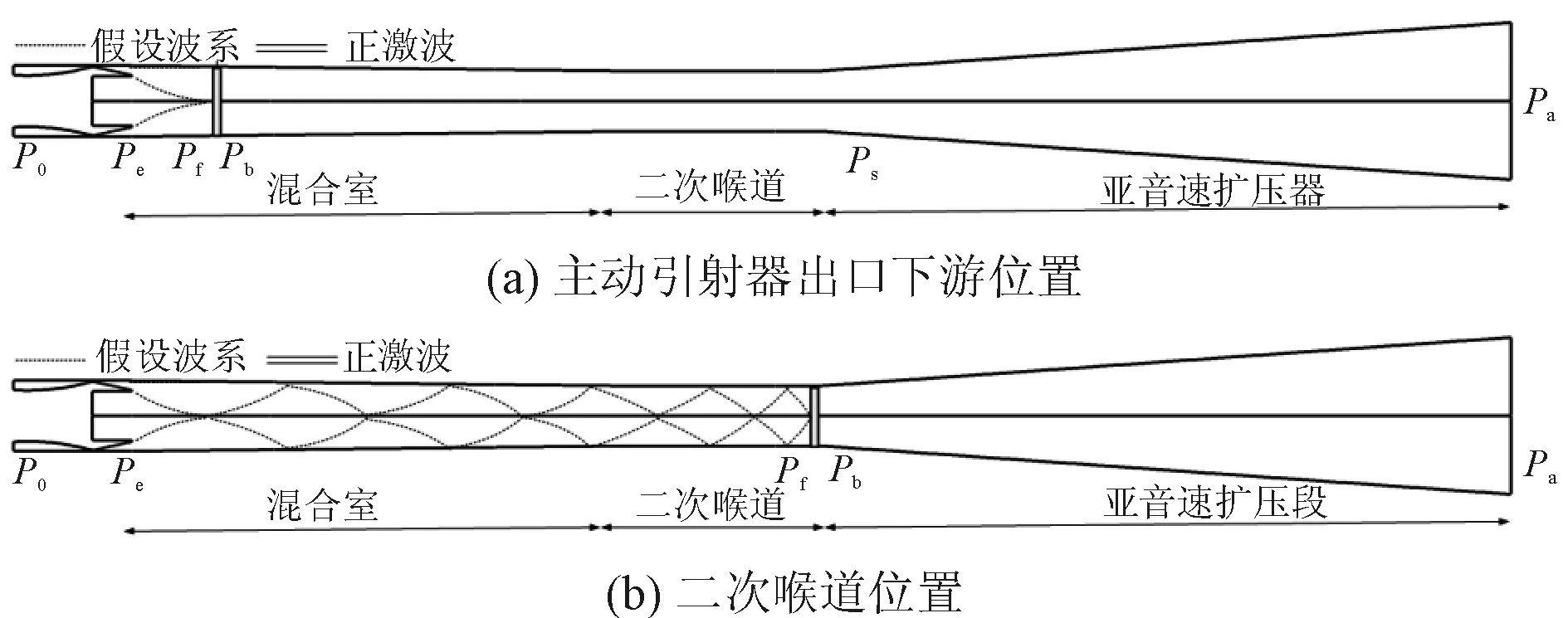
图7 正激波在主动引射器出口下游位置和二次喉道位置时的流动形态示意图

图7中平行双实线为正激波的波前和波后,单虚线为斜激波;P0为主动引射器喷管进口总压;Pe为引射器喷管出口静压;Pb为正激波波前静压;Pf为正激波波后静压;Ps为二次喉道静压;Pa为环境大气压。

图7(a)中,正激波位置处于主动引射器出口下有位置,整个流场的压力存在式(1)的关系。

(P0/Pa)st=(P0/Pf)×(Pf/Pb)×(Pb/Ps)×(Ps/Pa)

(1)

式中:P0/Pf是喷管喉部到正激波波前等熵膨胀的压缩比;Pf/Pb是正激波波前波后的静压比;Pb/Ps是正激波后到二次喉道的等熵压缩过程的静压比;Ps/Pa是二次喉道到扩压器出口的等熵膨胀过程的静压比。

对于正激波前后压缩比需要知道波前马赫数,波前马赫数可由式(2)[9]得到:

(2)

式中:Ad为混合室进口面积;At为主动引射器喷管喉部面积;Maf为扩压器进口的波前马赫数;k为比热比。

正激波波前和波后的静压比为:

(3)

按Pa=101.325 kPa计算,计算可得最小启动压力P0=1 218 kPa,与数值计算值1 240 kPa和实验测量值1 300 kPa的启动压力非常接近,误差在接受范围内,说明基于正激波理论的研究方法的计算结果是可靠和具有工程实用性的。

3.3.2 引射器最小保持启动状态的工作压力的理论计算分析

分析引射器的启动过程,引射器的迟滞效应中还存在一个能够保持引射器为启动状态的最小压力(即最小工作压力),引射器在该状态下工作可以节省大量气源,对该状态的引射器进口最小工作压力进行理论分析,可以用于快速预估引射器的性能。

图6计算结果显示,当主动引射器启动成功后,引射器进口总压逐渐减小,扩压器内的激波串向上游移动到二次喉道出口位置,继续减小为1 000 kPa的时候,二次喉道下游激波串逐渐消失,二次喉道中的激波变平直,成为一道较弱的正激波(如图7(b)所示),当该处的正激波即将不能维持时,主动引射器进口总压即为最小保持启动状态的压力,因此可以采用图7(b)中的状态来计算最小保持启动状态的压力。

图8是引射器启动过程中心线上马赫数变化曲线,可见当引射器为启动状态,在二次喉道正激波前,马赫数变化曲线完全重合,说明启动状态下混合室内和二次喉道内的马赫数只与通道结构参数有关,不受引射器进口总压的影响,由数值计算结果可得二次喉道处的正激波的波前马赫数为3.2,再由正激波理论可得波后马赫数为0.429 2,可得流量系数为q(λf)2=0.665 3。

图8 中心线上的马赫数变化

由主动引射器喉道和二次喉道处正激波波后的流量相等,流动过程假设为绝热流动,两处的总温相等得:

(4)

式中:K为常数;Qm为质量流量;P0为总压;A为流通面积;T0为总温;q(λ)为流量函数。

由式(4)可以推导出如下结果:

P0t1At1=P0t2At2q(λf)2

(5)

式中:P0t1、P0t2为引射器喷管进口总压和二次喉道正激波前总压;At1、At2为引射器喷管喉道面积和二次喉道面积。

已知P0t2=101.3 kPa,At2/At1=13.188 2,可得最小启动状态工作压力P0t1为889 kPa,该值与计算结果900 kPa非常接近,而与试验结果1 000 kPa相差100 kPa左右。与试验结果的误差可能是由于引射器保持启动的最小工作压力的这种流动状态非常不稳定,试验过程中稍微有一点扰动,主动引射器就变为不启动状态。

综上分析,对迟滞效应中的引射器的最小启动压力和最小保持启动状态的工作压力的正激波理论模型预测结果与数值计算和实验结果符合良好,该模型经过进一步的改进,在工程实践中具有一定的实用性。

4 结论

数值计算结果表明引射器启动特性与其内部的流动形态(激波位置)变化直接相关,而流动形态变化的驱动力由引射器进口总压提供。产生迟滞现象是由启动前和启动后的流动形态的转变过程所需能量不一样造成的。

正激波理论可以较准确预测最小的启动压力和最小的保持启动状态的工作压力。该理论模型有助于在设备研制过程中和试验中,确定引射器稳定工作的区间范围。

对于最小的保持启动状态的工作压力的计算,混合室内复杂的激波系导致在二次喉道正激波波前马赫数的理论计算结果求解困难,文中是通过数值计算方法得到二次喉道正激波波前的马赫数。今后可以通过分析混合室内部的激波串的长度和个数等特征,继续开展计算混合室内的复杂波系的出口马赫数的工作,找到相关理论模型,进而不需要数值计算结果即能够预测引射器的最小保持启动状态的压力。

参考文献:

[1] KIM S, KWON S. Experimental investigation of an annular injection supersonic ejector [J]. AIAA Journal, 2006, 44(8): 1905-1908.

[2] AOKI S, LEE J, GORO M. Aerodynamic experiment on an ejector-jet [J]. Journal of Propulsion and Power, 2005, 21(3): 496-503.

[3] 吴继平, 陈健, 王振国. 多喷嘴超声速引射器启动性能试验研究 [J]. 推进技术, 2008, 29(2): 174-178.

[4] PARK Geunhong, KIM Sehoon, KWON Sejin. A starting procedure of supersonic ejector to minimize primary pressure load [J]. Journal of Propulsion and Power, 2008, 24(3): 631-635.

[5] 徐万武, 谭建国, 王振国. 高空模拟试车台超声速引射器数值研究 [J]. 固体火箭技术, 2003, 26(2): 71-74.

[6] 徐万武, 邹建军, 王振国, 等. 超声速环型引射器启动特性试验研究 [J]. 火箭推进, 2005, 31(6): 7-11

[7] 杨建文, 付秀文, 刘占一, 等. 等截面引射器启动性能数值研究 [J]. 应用力学学报, 2014, 31(5): 697-702.

[8] 吴继平. 高增压比多喷管超声速引射器设计理论、方法与实验研究 [D]. 长沙: 国防科学技术大学, 2007.

[9] ANDERSON J D. Modern compressible flow with historical perspective [M]. 3rd ed. New York: McGraw-Hill, 2003.