误差源对半捷联导引头信息提取精度的影响

李 然, 温求遒, 洪 超, 夏群利

(1 北京理工大学, 北京 100081; 2 中国兵器工业集团公司, 北京 100091)

0 引言

导引头平台稳定技术是精确制导武器的核心技术之一,它直接关系到武器的制导精度[1-2]。因此如何提高稳定平台的精度已成为提高武器系统精度的重要手段。随着传感器技术和加工工艺的飞速发展,传统的速率陀螺稳定平台[3]整体性能也得到了质的飞跃,并在几乎所有种类的导引头内得到了应用。近年来,随着武器系统向低成本、小型化趋势的发展,对导引头稳定平台技术的研究重心已开始转向半捷联导引头稳定技术,而且在国外已有采用该技术的产品装备部队,如德国的KEPD-350防区外发射空地导弹、IRIS-T先进近距格斗空空导弹等[4-6]。其原理是根据当前的框架角和导弹捷联惯导采用的惯性测量组合(IMU)输出的信息,对导引头视线进行稳定[7-8]。同陀螺稳定平台比较,其优势非常明显:由于没有速率陀螺传感器,大大降低了导引头成本;在结构编排和加工工艺方面也大为简化,为导引头的小型化设计提供了更大的空间。文献[9]、文献[10]主要研究了图像半捷联导引头制导信息的构造方法,采用UKF(uncented Kalman filter)滤波方法对框架角速率进行了估计。文献[11]在弹体扰动下,将光轴指向看作矢量,进行半捷联寻的制导系统的光轴补偿稳定。文献[12]、文献[13]对比分析了平台稳定导引头和半捷联导引头的光轴稳定控制方案,进行了视线扰动和传感器噪声对稳定控制回路性能的影响分析。文献[14]提出采取匹配滤波方法提高捷联稳定平台解耦精度并对匹配滤波器参数进行优化设计及仿真。文献[15]、文献[16]对干扰力矩和弹体扰动及本身结构参数的变化对半捷联稳定平台的影响进行了分析,并提出了双环滑模变结构控制器稳定平台方案。

文中基于半捷联稳定平台制导体制,建立了半捷联导引头模型,利用空间角度关系推导了基于角速度控制数学模型,利用四元数法推导了框架角控制数学表达式,同时针对平台框架角速度误差、视线角速率提取误差进行了分析,并进行数学仿真,结合仿真数据得出各因素的影响程度,所得结论对半捷联导引头实际工程设计及指标参数选取具有一定的指导意义。

1 半捷联导引头建模

1.1 坐标系定义

1)惯性坐标系(i):oixiyizi原点在地球中心,近似看作固定于惯性空间的坐标系,是惯性元件测量的参考基准;

2)弹体坐标系(b):obxbybzb原点在弹体重心,xb沿弹体纵轴向前,yb沿弹体航向轴向上,zb按右手定则沿弹体横轴向右;

3)导引头伺服平台坐标系(p):opxpypzp原点在伺服平台回转中心,xp沿光轴向前,yp沿伺服平台航向轴向上,zp按右手定则沿伺服平台横轴向右;

4)末制导坐标系(g):ogxgygzg原点在弹体重心,xg沿弹目连线并指向目标,当导引头稳定跟踪目标时,yg与yp平行、zg与zp平行;

5)图像跟踪坐标系(t):otxtytzt原点在视场中心,各轴与平台坐标系(p)的各轴平行。

1.2 半捷联导引头控制原理

半捷联导引头闭环跟踪与控制原理框图如图1所示。

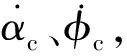
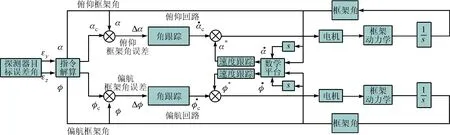
图1 半捷联导引头闭环跟踪与控制原理框图

图2 简化的稳定平台跟踪控制原理框图

目标在探测器上角误差εz、εy定义如图3所示。

图3 目标在导引头探测器上的角误差示意图

2 导引头伺服平台控制

2.1 速率回路控制

(1)

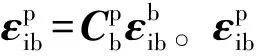
文中所研究的稳定平台为方位、俯仰两框架结构,且俯仰框为内框,所以有:

(2)

因为方位电位计与弹体固联,所以方位电位计测量的矢量在弹体坐标系(b)内;俯仰电位计既不位于弹体上也不位于伺服平台上,而是位于方位框架上,所以测量的矢量在方位框所确定的中间坐标系(m)内,具体转换矩阵如下:

(3)

(4)

(5)

由式(4)、式(5)可得:

(6)

(7)

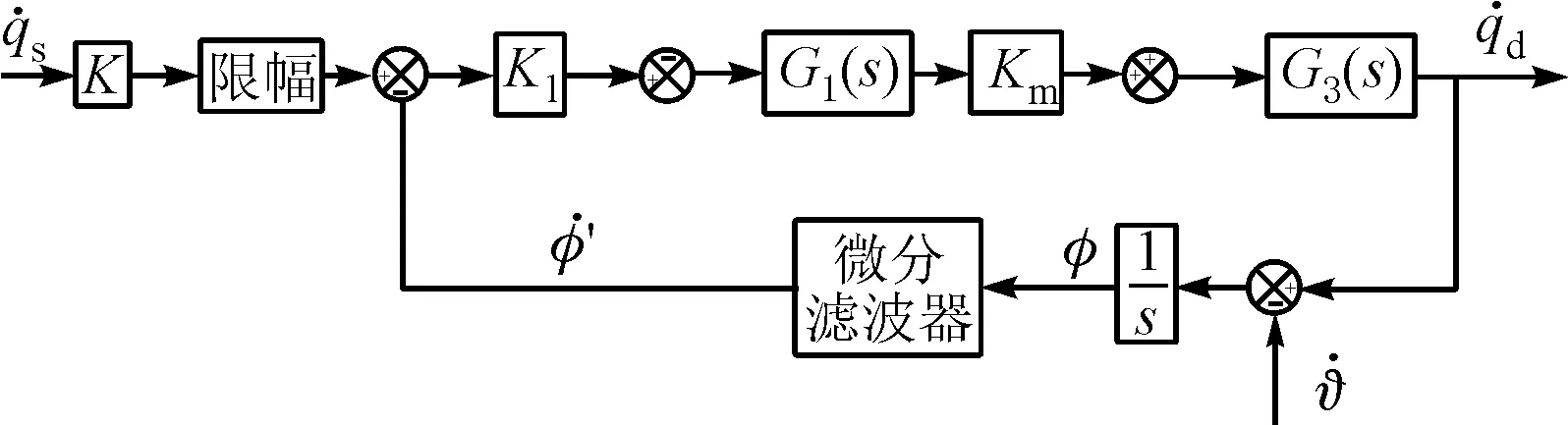
图4 框架角速度控制回路

2.2 角度回路控制

以导引头初始跟踪时伺服平台所处的空间角度作为初始的末制导坐标系(g),考虑到末制导坐标系转换到弹体坐标系的转换顺序是:由末制导坐标系(g)依次转动航向ψ、俯仰θ、横滚γ到达弹体坐标系(b),而平台系(p)转换到弹体系(b)的顺序为:由平台系(p)依次转动平台俯仰φ、平台方位α、平台横滚γ′(γ′=0)到达弹体坐标系(b)。两个转换顺序不同,但为了计算方便,可以将航向ψ和俯仰θ交换信号并表示为“航向ψ1”和“俯仰θ1”,以适应伺服平台的框架结构,相当于将IMU在弹轴方向转动90°安装,这样如下关系就可以成立。

ψ1=α,θ1=φ,γ=0

(8)

由此,确定对姿态导航矩阵的四元数修正算法中四元数的初始值:

设弹体系(b)到末制导坐标系(g)的转换矩阵为:

(9)

式中:

四元数修正算法如下(忽略位置速率ωeg和地球速率ωie):

(10)

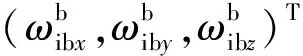
又令平台系(p)与末制导系(g)平行,则可建立如下含未知数αc、φc的方程:

(11)

展开如下:

(12)

由式(12)不难得到求出伺服平台指令的表达式:

3 半捷联导引头误差分析

3.1 框架角速度指令转换误差

框架角速度指令的坐标系转换计算公式为:

(13)

(14)

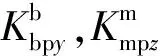
a)方位、俯仰角度误差为+0.1°。方位速度误差和俯仰速度误差分别如图5、图6所示(两个水平轴分别表示方位、俯仰框架角((°));纵轴表示转换造成的角速度误差与弹体扰动角速度的比值)。计算可得方位误差范围为[-0.125%,+0.13%],俯仰误差范围为[-0.238%,-0.062%]。

图5 方位速度误差

图6 俯仰速度误差

b)方位角度误差为-0.1°、俯仰角度误差为+0.1°时,方位误差及俯仰误差如图7、图8所示。由图中可以看出偏航误差范围为[-0.34%,+0.18%],俯仰误差范围为[+0.062%,+0.238%]。

图7 方位速度误差

图8 俯仰速度误差

c)方位角度误差为+0.1°、俯仰角度误差为-0.1°时,方位误差如图9所示,误差范围为[-0.18%,+0.34%]。俯仰误差和第一种情况一致。

图9 方位速度误差

d)方位、俯仰角度误差为-0.1°时,方位误差如图10所示,误差范围为[-0.13%,+0.125%]。俯仰误差与第二种情况相同。

图10 方位速度误差

综合上述情况,可以得出:框架角速度指令误差的大小除了取决于框架测角误差,还取决于弹体的扰动大小。当方位、俯仰框架均处于±30°以内,且测角误差为±0.1°时,因坐标系转换带来的速度误差与弹体扰动角速度的比值方位为[-0.34%,+0.34%],俯仰为[-0.238%,+0.238%]。如果只考虑末制导段的角速度误差,假设弹体的最大扰动达到20°/s,框架上的角速度最大误差为:方位=0.068°/s;俯仰=0.0476°/s。由于平台伺服控制具有阻尼特性,不会受到太大的误差的影响,只会使得速度控制精度下降不到0.07°/s。

3.2 角速度计算误差

(15)

俯仰电位计处理出的角速度转换到弹体坐标系后的角速度为:

(16)

于是:

(17)

按照±0.1°的测角误差,可以绘出两条误差曲线,如图11所示。

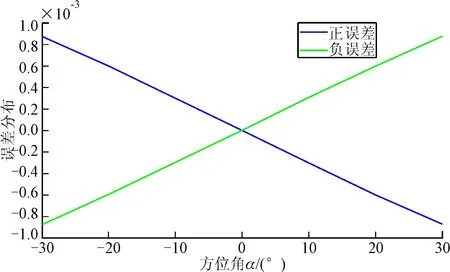
图11 角速度测量误差

3.3 匹配滤波误差对控制精度的影响

使用相同的伺服放大器、电机和平台控制对象,分别建立陀螺稳定和捷联稳定速率控制回路的单通道简化仿真模型。

陀螺稳定平台的单通道速率稳定回路控制模型表示如图12所示。

图12 陀螺稳定平台速率稳定控制回路

通过图12可以推导出弹体扰动输入到平台角速率输出的传递函数为:

(18)

捷联稳定平台的速率稳定回路控制模型表示如图13所示。

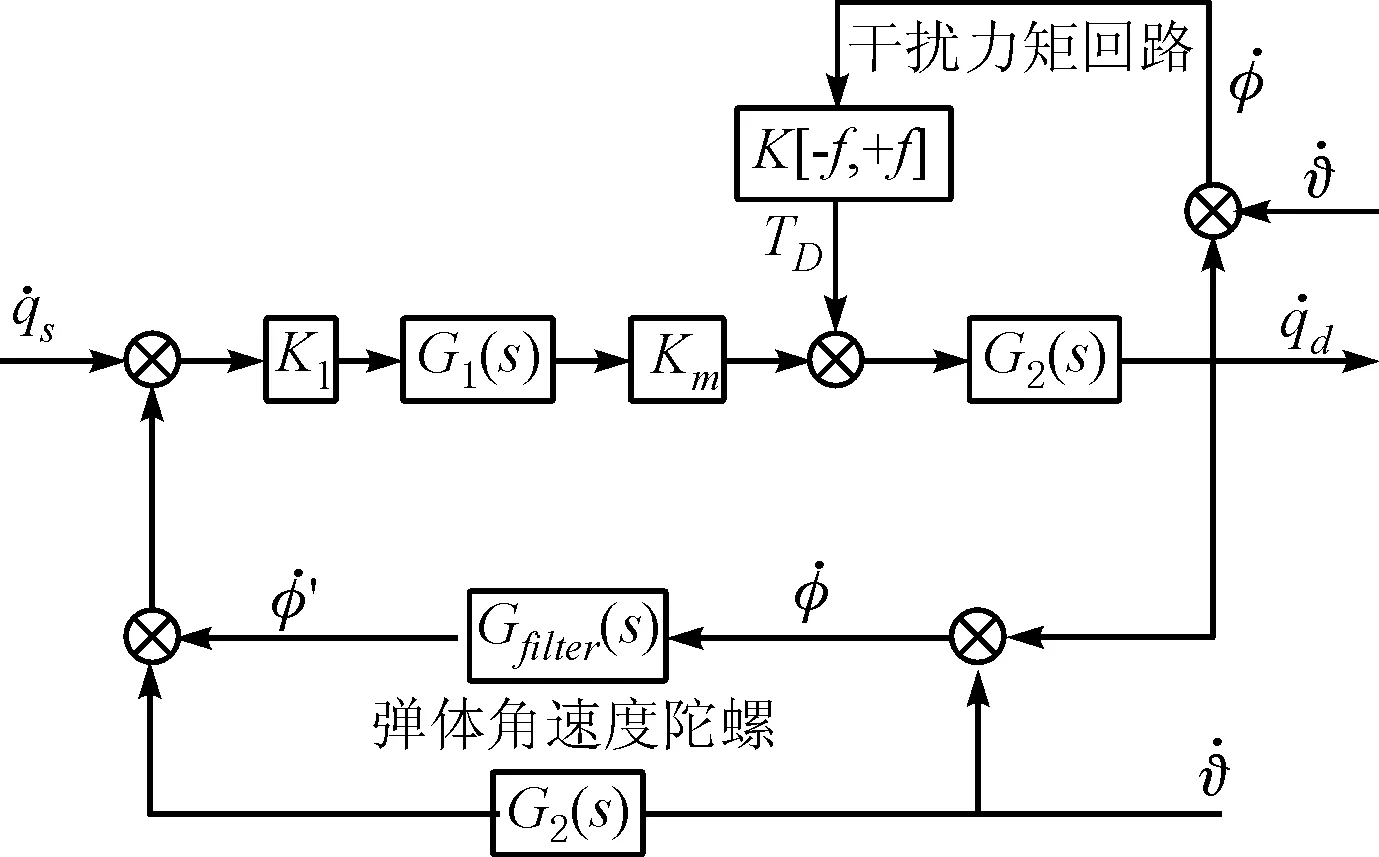
图13 捷联稳定平台速率稳定控制回路

其中Gfilter(s)表示滤波器传函。

通过该模型可以推导出弹体扰动输入到平台角速率输出的传递函数:

(19)

K1KmG1(s)(Gfilter(s)-G2(s))+K[-f,+f]→0

K[-f,+f]需要靠工艺来尽可能减小,而Gfilter(s)-G2(s)→0是可以做到的,所以,只要满足Gfilter(s)与G2(s)的传递函数相等,就可以消除该项扰动分量,实现和陀螺稳定平台相当的稳定精度。

匹配精度影响最大的是隔离度,对视线角速度测量没有大的影响,因为弹体制导控制的带宽通常小于3 Hz,只要能找到一种方法进行最佳匹配,就能使平台的稳定性能接近陀螺稳定平台的水平。

图14 陀螺稳定平台的角速率控制误差

图15 时间常数为1 ms角速率控制误差

同样条件下,半捷联稳定平台的响应与滤波时间常数有关,图15～图18分别给出了不同时间常数下的角速率控制误差。

由图14～图18可知,半捷联稳定方式的稳定精度较陀螺稳定方式在多数情况下差四倍左右;但是,当滤波时间常数为3 ms时控制精度急剧提高,接近陀螺稳定平台的控制精度;当修改滤波时间常数和陀螺时间常数,可以发现仅当滤波时间常数与陀螺时间常数相同时稳定平台具有最佳的控制精度。

图16 时间常数为3 ms角速率控制误差

图17 时间常数为5 ms角速率控制误差

图18 时间常数为10 ms角速率控制误差

4 结论

文中通过建立相应的坐标转换关系推导了半捷联平台控制的数学模型,同时,针对不同误差环节作了量化分析,所得结论如下:

1)导致平台框架角速度误差的误差源包括了IMU的测速误差、框架位置传感器的测角误差以及因此而导致的角速度指令的转换误差。对平台控制而言,这些误差产生的影响是不大的,会导致速度控制精度下降不到0.07°/s。

3)对平台稳定性能的影响取决于校正控制回路的设计和匹配滤波器的设计,特别是匹配滤波器的设计,对平台稳定精度的影响很大,好的设计可以明显提高平台的隔离度。

参考文献:

[1] 王黎光, 景占荣, 王玲玲. 拦截弹导引头测量误差对拦截效能的影响 [J]. 系统工程与电子技术, 2012, 34(3): 578-581.

[2] CHAUDHURY B, CHATURVEDI S. Study and optimization of plasma based radar cross section reduction using three-dimensional computations [J]. IEEE Transactions. on Plasma Science, 2009, 37(11): 2116-2127.

[3] 林忠贤, 杨晨. 空空导弹导引头位标器质量不平衡对制导精度的影响 [J]. 电光与控制, 1997(2): 24-29.

[4] 胡洋, 彭晓乐, 王宏宇. 半捷联式稳定平台隔离度影响因素分析 [J]. 电子设计工程, 2010, 18(5), 72-75.

[5] 樊会涛, 刘代军. 红外近距格斗空空导弹发展展望 [J]. 红外与激光工程, 2005, 34(5): 564-568.

[6] 牟宏山. InSb红外焦平面探测器现状与进展 [J]. 激光与红外, 2016, 46(4): 394-399.

[7] JANG S A, RYOO C K, CHOI K Y, et al. Guidance algorithms for tactical missiles with strapdown seeker [C]∥ IEEE. Proceedings of 2008 the Society of Instrument and Control Engineers Annual Conference.[S.l.]:SICE, 2008: 2616-2619.

[8] GUO T, XIA Q L, QI Z K. Study on strapdown decoupling technology for rolling missile using RF interferometer seeker [C]∥IEEE. Proceedings of 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics. [S.l.]:IEEE, 2010: 823-828.

[9] 宋建梅, 孔丽霞, 范健华. 半捷联图像寻的制导系统导引信息构造方法 [J]. 兵工学报, 2010, 31(12): 1573-1579.

[10] 姜竹青. 自主导航中滤波算法的研究及应用 [D]. 北京: 北京邮电大学, 2014.

[11] 毛峡, 张俊伟. 半捷联导引头光轴稳定的研究 [J]. 红外与激光工程, 2007, 36(1): 9-12.

[12] 杨哲, 林德福, 祁载康. 考虑雷达导引头前馈补偿的一体化制导方法 [J]. 系统工程与电子技术, 2016, 38(6): 1352-1359.

[13] KENNEDY P J， KENNEDY R L. Direct versus indirect line of sight (LOS) stabilization [J]. IEEE Transactions on Control Systems Technology, 2003，11(1)： 3-15.

[14] 张聘义, 祁载康, 崔莹莹, 等. 一种匹配滤波方法在导引头捷联稳定平台中的应用研究 [J]. 红外技术, 2005, 27(1): 6-11.

[15] 刘伟, 柯芳, 朱斌, 等. 半捷联导引头稳定平台的双环滑模变结构控制 [J]. 兵工学报, 2010, 31(12): 1669-1673.

[16] 张跃, 储海荣. 半捷联导引头机电平台观测器的角速率估计 [J]. 红外与激光工程, 2015, 44(12): 3794-3800.