一种改进的容积信息粒子滤波多目标跟踪算法

赵毅寰, 陈 伟, 刘 哲, 沈 康

(1 中国空空导弹研究院, 河南洛阳 471009; 2 航天恒星科技有限公司, 北京 100086;3 北京航空航天大学电子信息工程学院, 北京 100191)

0 引言

粒子滤波是近年来出现的一种非常优秀的多目标跟踪方法。与传统的卡尔曼滤波算法不同,粒子滤波不受高斯假设前提的限制,适用于非高斯场景下目标的跟踪。目前粒子滤波已广泛应用于分布式融合[1]、地面目标跟踪[2]、红外目标跟踪[3]、扩展目标跟踪[4],同时定位与地图构建(simultaneous localization and mapping,SLAM)[5]等领域。

为提高粒子滤波算法的性能,国内外学者提出了一系列改进算法。Pitt[5]提出了辅助粒子滤波算法,通过引入辅助变量计算重要性采样函数,使得粒子权值的均方根误差最小。在此基础上,Lee[6],Baser[7],Isaac[8]等使用不同方法对辅助粒子滤波算法进行改进,并获得了很好地跟踪效果。但是当目标跟踪场景出现强噪声和非线性运动,上述算法将出现较大的跟踪误差。

近年来,容积卡尔曼滤波(CKF)在非线性目标跟踪得到广泛的应用。容积信息滤波(CIF)算法在多量测非线性目标跟踪下具有稳定的跟踪性能,因此文中将CIF和Gating技术应用于粒子滤波的重要性采样函数的设计中,提出了容积信息粒子滤波(CI-PF)算法,通过计算统计距离,并设定相应的阈值,建立粒子与量测的关联关系。与常规方法相比,CI-PF具有跟踪结果稳定、精度高的优点。

1 粒子滤波算法概述

粒子滤波是一种序贯蒙特卡洛算法,其基本思想是将目标的概率分布表示成一组具有不同权值的粒子求和。通过更新粒子的权值,从而完成目标状态的估计。

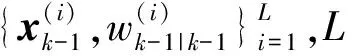
1)计算k时刻的粒子状态与权值。

(1)

(2)

2)更新式(2)的预测权值。

(3)

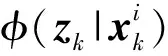
2 容积信息粒子滤波算法

2.1 问题描述

设非线性目标的运动方程和量测方程可以表示为:

状态方程：xk=f(xk-1)+vk-1

量测方程：zk=h(xk)+nk

(4)

式中:f(·)和h(·)分别为目标的状态转移和量测函数;vk-1为k-1时刻的状态噪声;nk为k时刻量测噪声。通常情况下,vk-1和nk选择为零均值高斯白噪声,其对应的协方差矩阵分别为Qk-1和Rk。

根据式(4),文中选择重要性采样函数如下:

(5)

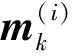
2.2 CIF重要性采样函数估计

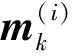
1)容积点传播。

(6)

式中χk-1,j代表第j个容积点,且:

(7)

(8)

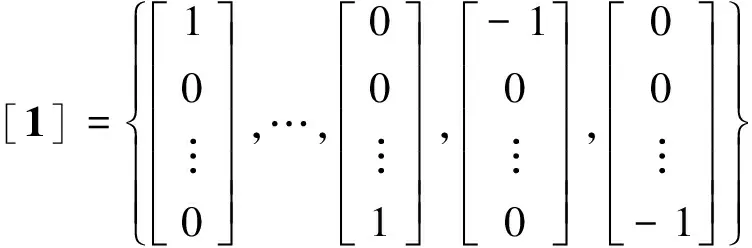
式(8)中,d为mk-1的维数,向量[1]j为集合[1]的第j个向量。

2)状态及协方差矩阵均方根预测。

(9)

(10)

对应信息形式如下:

yk|k-1=Yk|k-1mk|k-1

(11)

Yk|k-1=(Pk|k-1)-1

(12)

3)量测及其协方差矩阵预测。

式中:

(15)

(16)

4)k时刻信息形式计算。

(17)

(18)

式中:Zk为当前量测集,zk,j∈Zk,

5)k时刻的状态和协方差矩阵估计。

通过式(22)～式(23)便可以得到mk和Pk,利用式(5)从而可以计算重要性采样。在此基础上,使用第1节的粒子滤波算法,便可以完成多目标状态和目标数目估计。

2.3 基于Gating技术的量测关联

式(17)在计算信息形式时,使用了当前量测集Zk的所有量测。但在实际场景中,受杂波、虚警等因素的影响,当前量测集往往为目标和杂波的组合。大量杂波的存在不仅影响估计精度,而且耗费大量计算资源。通常情况,粒子预测量测周围的量测与粒子状态具有较大概率的关联性。为此,文中使用Gating技术,通过对统计距离设定合理的门限值,提取与当前粒子关联性较大的量测进行式(17)的计算。对量测zk,j和zk|k-1,其统计距离可以表示为

(24)

利用式(24)计算当前量测集的量测与zk|k-1的统计距离,在此基础上,选择合理的阈值Th,提取与粒子关联性较大的量测,如下式。

(25)

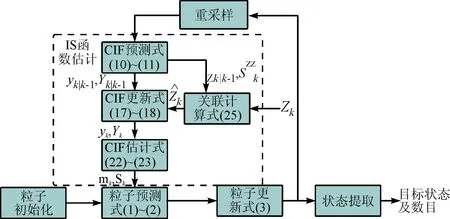
图1 CI-PF算法执行流程

在文中的算法中,使用多项式重采样作为重采样策略。

3 仿真实验

本节将对BPF和文中提出的CI-PF算法分别进行仿真分析。为验证算法的有效性,这里采用最优次模式分配(OSPA)距离和RMSE作为衡量标准。

3.1 场景设定

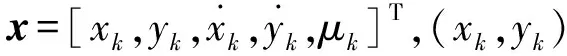
(26)

对应的量测为:

(27)

初始状态参数如表1所示。目标存活概率ps(xk)=0.99,检测概率pd(xk)=0.95,统计距离门限Th=16,每个目标对应的粒子数为100。

表1 目标的初始参数

3.2 实验结果及分析

图2为待估计目标的轨迹,杂波数为20。分别使用CI-PF和BPF算法对图2中的目标进行跟踪,蒙特卡洛仿真500次,估计结果如图3和图4所示。可以看出,CI-PF估计轨迹中大部分粒子与真实目标轨迹重叠,而BPF在跟踪时出现了大量漏跟踪的情况。

为进一步分析估计误差,分别给出了二者的OSPA距离和跟踪目标数目RMSE,见图5和图6。图5中,CI-PF的平均OSPA距离为28.98,BPF则为74.06。从图5可以看出,在整个跟踪过程,CI-PF的OSPA距离小于BPF,这表明CI-PF算法的精度优于BPF。从图6的RMSE曲线可以看出,和BPF相比,CI-PF的目标数目更接近于真实目标数目。上述结果的出现是因为CI-PF算法将当前量测引入重要性采样函数,并使用CIF和Gating技术提高了估计的精度,因而更适用于非线性多目标跟踪场景。

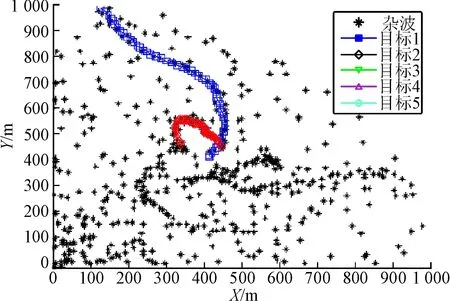
图2 待估计目标轨迹

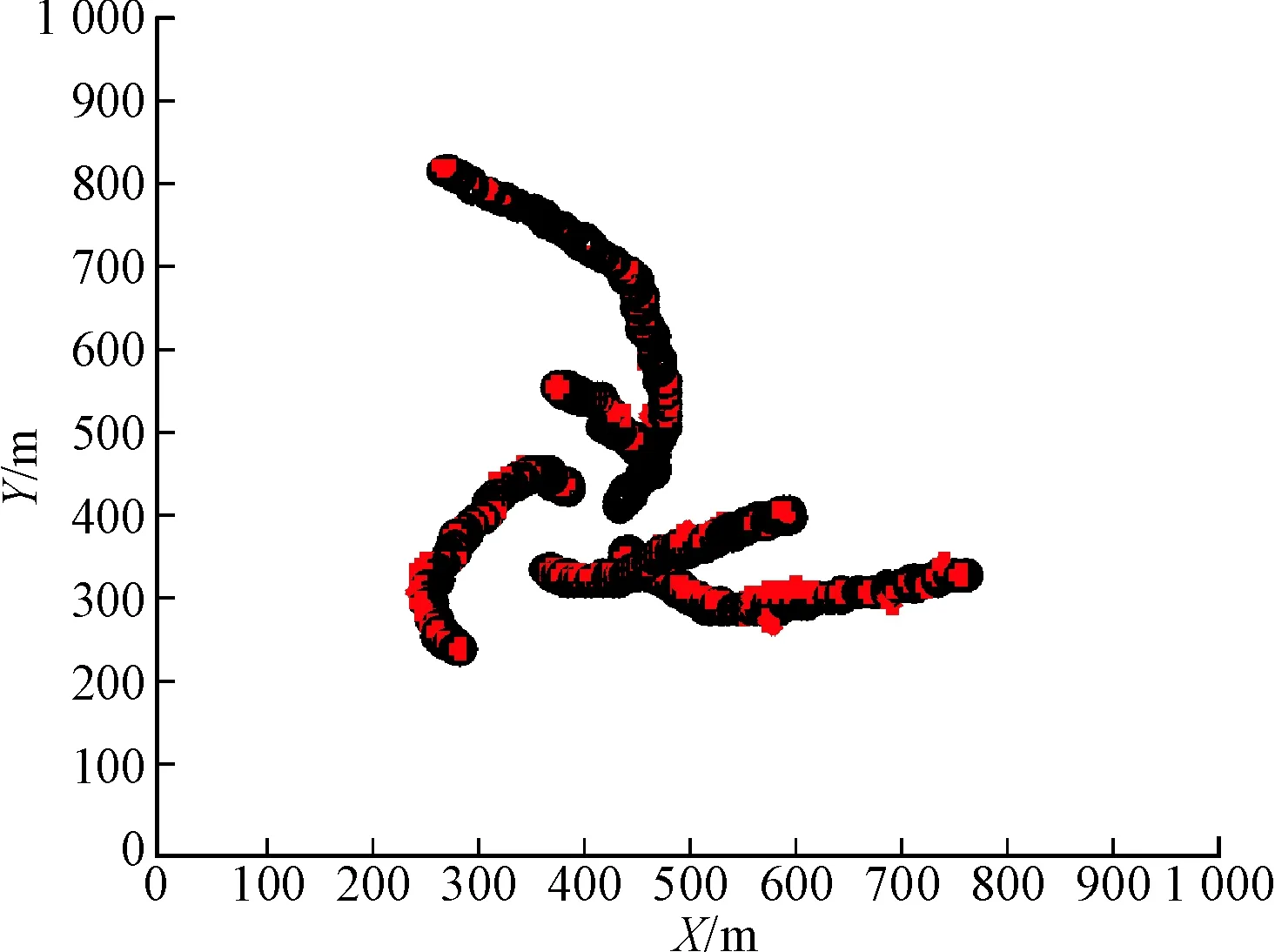
图3 CI-PF估计轨迹

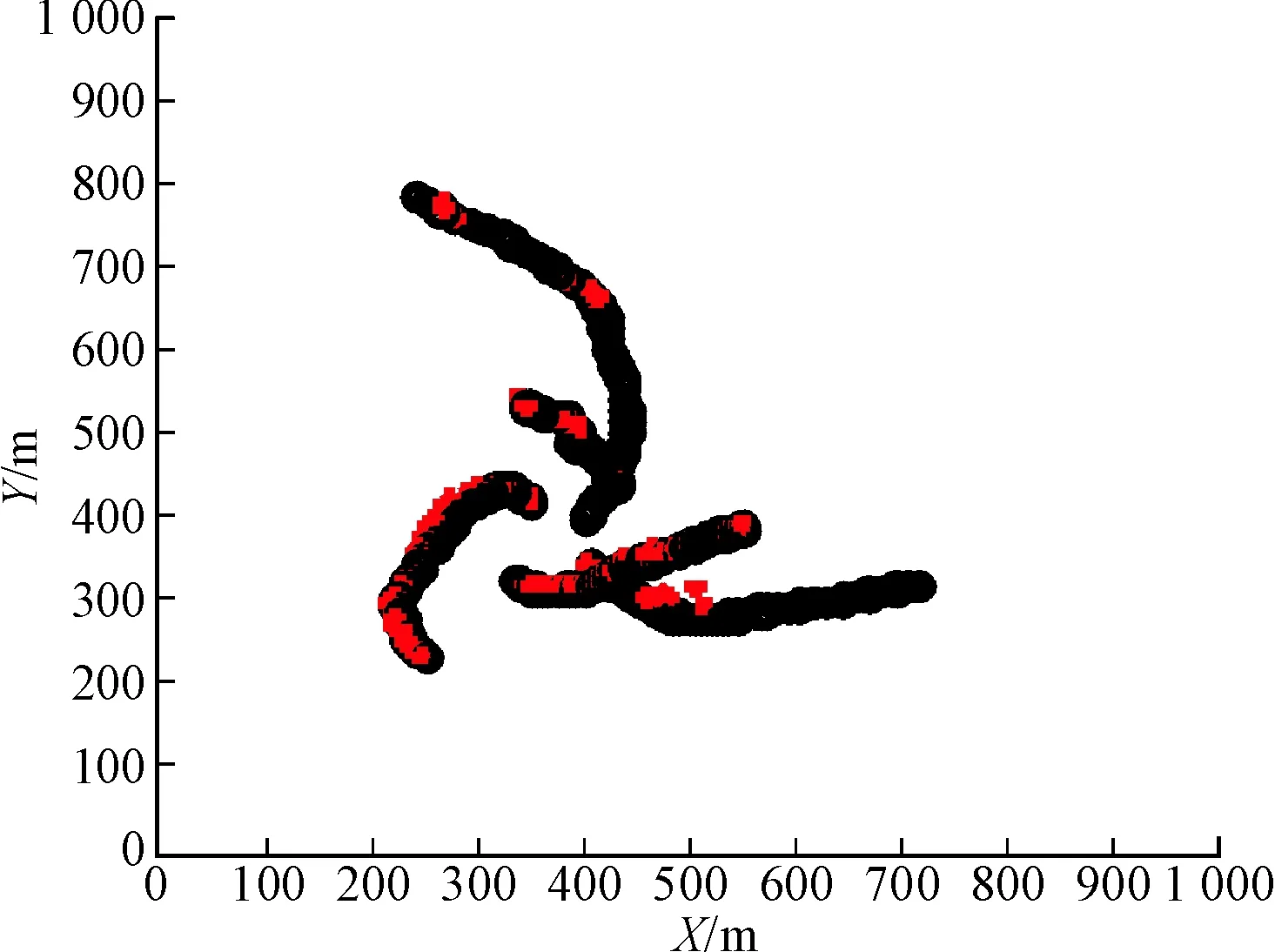
图4 BPF估计轨迹

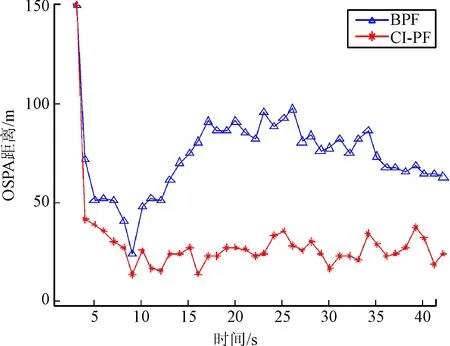
图5 CI-PF与BPF估计OSPA距离

4 结论

针对常规自举式粒子滤波在非线性目标跟踪场景精度差的缺点,通过重要性采样函数的设计,提高粒子滤波的跟踪精度。具体而言,首先使用后验概率密度作为粒子滤波算法的重要性采样函数,而后使用CIF方法估计重要性采样函数的均值和协方差矩阵,完成重要性采样函数的设计。此外,为建立粒子与当前量测集的关联关系,引入Gating技术,通过计算统计距离并设定相应的阈值,提取相关的量测用于重要性采样函数的计算,从而减少运算量。CI-PF算法通过结合CIF和Gating技术,避免了自举式粒子滤波在非线性跟踪场景下粒子群退化,跟踪性能下降的问题。仿真实验表明,CI-PF算法的跟踪性能优于BPF。

图6 CI-PF与BPF的RMSE

参考文献:

[1] ÜNEY M, CLARK D E, JULIER S J. Distributed fusion of PHD filters via exponential mixture densities [J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 521-531.

[2] LIU Z, WANG Z, XU M, et al. A novel CIF-based SMC-PHD approach for tracking multiple nonlinear targets [C]// IEEE. 2015 IEEE Radar Conference (RadarCon).[S.l.:s.n.], 2015: 555-560.

[3] 王玲玲, 辛云宏. 基于形态学与遗传粒子滤波器的红外小目标检测与跟踪算法 [J]. 光子学报, 2013(7): 849-856.

[4] MIHAYLOVA L, CARMI A Y, SEPTIER F, et al. Overview of Bayesian sequential Monte Carlo methods for group and extended object tracking [J]. Digital Signal Processing, 2014, 25(1): 1-16.

[5] 宋宇, 李庆玲, 康轶非, 等. 平方根容积Rao-Blackwillised粒子滤波SLAM算法 [J]. 自动化学报, 2014, 40(2): 357-367.

[6] PITT M K, SHEPARD N. Filtering via Simulation: Auxiliary Particle Filters [J]. Journal of the American Statistical Association, 1999, 94(446): 590-599.

[7] LEE S M, JUNG J, KIM S, et al. DV-SLAM (Dual-Sensor-Based Vector-Field SLAM) and observability analysis [J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 1101-1112.

[8] BASER E, EFE M. A novel auxiliary particle PHD filter [C]// IEEE. 2012 15th International Conference on Information Fusion (FUSION). Singapore: IEEE Press, 2012: 165-172.

[9] ISAAC A, WILLETT P, BAR-SHALOM Y. Quickest detection and tracking of spawning targets using monopulse radar channel signals [J]. IEEE Transactions on Signal Processing, 2008, 56(3): 1302-1308.

[10] LI Liangqun, JI Hongbing, LUO Junhui. The iterated extended Kalman particle filter [C]∥ IEEE. 2005 International Symposium on Communications and Information Technology.[S.l.:s.n.], 2005: 1213-1216.

[11] MOHAMMADI A, ASIF A. Consensus-based distributed unscented particle filter [C]// IEEE. 2011 IEEE Statistical Signal Processing Workshop (SSP). Nice:IEEE, 2011: 237-240.

[12] 常天庆, 李勇, 刘忠仁, 等. 一种改进重采样的粒子滤波算法 [J]. 计算机应用研究, 2013, 30(3): 748-750.

[13] CHANDRA K P B, GU D W, POSTLETHWAITE I. Square root cubature information filter [J]. IEEE Sensors Journal, 2013, 13(2): 750-758.

[14] 曹有亮, 张金鹏. 扩展卡尔曼滤波器的目标机动信息估计研究 [J]. 航空兵器, 2016(1): 40-44.