反辐射导弹抗海上机动目标关机仿真研究

刘家祺, 谢晓方, 孙 涛, 梁 捷, 曹 建

(海军航空工程学院, 山东烟台 264001)

0 引言

反辐射导弹采用宽频被动雷达导引头,是压制防空系统的硬杀伤武器。它本身不辐射电磁波,具有很强的隐蔽性。在近几次局部战争中,ARM和隐形战机搭配充当了“踹门者”角色,逐渐得到了世界各军事大国的重视。美国和日本目前正在积极研制和试验反舰型的反辐射导弹,以增强未来海战中先发制人的能力。ARM理论上可以打击水面舰艇制导雷达和警戒雷达。陆基雷达位置一般固定不变,如果目标雷达临时关机,ARM仍可以通过惯导实现记忆攻击,而海上目标可随舰艇机动,关机后ARM能否达到预定作战效果还有待研究。当前抗关机能力研究大多数针对静止目标,而且主要集中在惯导误差、无源定位误差以及卡尔曼滤波器等影响因素上[1-3],对机动目标抗关机能力研究很少[4-5]。文中在考虑了上述误差的基础上,重点针对水面舰艇的机动性以及舰载雷达的架设特点对ARM的命中概率进行了仿真研究。

1 舰艇目标机动规避范围

关机时刻导弹位于M点,目标位于T点,弹目距离为d,导弹飞行速度为VM,导弹对目标速度估计为VT,如果忽略目标速度估计误差,且目标保持速度VT直线运动,导弹目标相遇时目标到达点T′,点T到点T′的距离为R。以T点为原点,VT正方向为x轴正方向,垂直于x轴向上为y轴正方向,建立目标航向坐标系T-xy,如图1所示。

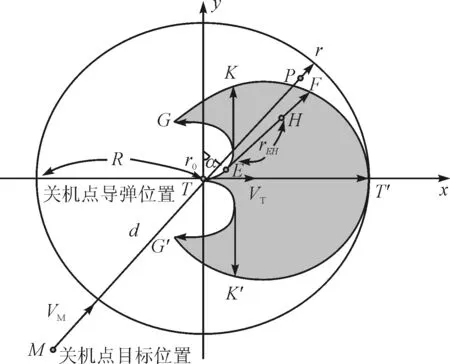
图1 目标雷达关机后机动范围

(1)

这种曲线在解析几何上称为渐伸线[6],上下边界曲线分别为中心点在y轴上下半轴半径为r0的两个圆的渐伸线,旋转方向相反。

图1中,点H(xH,yH)在EF上,EF长度为REF=R-|α|r0,EH长度rEH(0≤rEH≤REF),点H可以表示月牙形区域TGT′G′内任何一点,点H极坐标形式为(α,rEH)。取一个dα和drEH范围内的面积元,其面积为rEHdαdrEH,区域TGT′G′的面积为:

(2)

如果假设点H在整个月牙形状区域TGT′G′内均匀分布,那么H点概率密度函数为:

(3)

如果假设α服从均匀分布,rEH也服从均匀分布,那么H点概率密度函数为:

(4)

2 目标随机转弯机动模型

上一节假设目标在T点立即转弯和速率不变,本节进一步细化模型。假设目标发现反辐射导弹后关机并且机动规避,采取满舵方式进行最大幅度的转弯机动,转过一个随机角度后保持运动方向不变,目标最终位置在能达到的最远点以内随机分布。

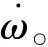
(5)

忽略高阶项,Mδ≈a·δ,Mβ≈b·ω,其中a为转船力矩系数,b为阻尼力矩系数,IO/b=T,a/b=K,则上式可转化为:

(6)

式(6)就是野本谦作的一阶近似操纵运动方程式[7-8]。K为旋回性指数,T为追随性指数,ω为旋回角速度,δ为舵角。将K、T指数作无量纲化处理:

K′=K·L/Vt,T′=T·Vt/L

(7)

式中:L为船长;Vt为稳定时的旋回速度。操舵至δ0所需时间为t1,计算旋回圈参数定常旋回半径R0和心距Re公式为:

(8)

Re=Vt(T+t1/2)

(9)

旋回圈轨迹如图2所示。O点为开始转舵时目标位置,I点和E点分别为旋回圈的入点和出点,在α方位上以速度Vmax能够到达最远点F。

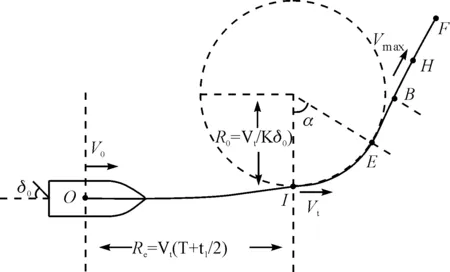
图2 目标旋回圈轨迹

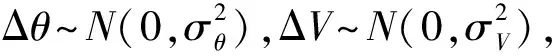
(10)

Re段的加速度为:

(11)

如果Δt≤tRe,目标最终位置点H尚在Re段:

(12)

如果Δt>tRe,αmax=min{Kδ0(Δt-tRe),π},不妨设α服从均匀分布,即α～U(-αmax,αmax),且若Δt足够目标转过α角,目标最终位置H在直线EF上也服从均匀分布。用Vmax和Δt来估计F点,即REF=Vmax(Δt-tRe-α/Kδ0),rEH～U(0,REF)。随机角α对应的E点坐标为:

(13)

目标最终位置点H坐标为:

(14)

3 反辐射导弹命中概率

3.1 反辐射导弹末端随机弹道方程

在目标雷达关机时间内,ARM将根据惯性和卫星导航系统的信号控制导弹,飞向弹上计算机预测的目标位置T′。CEP为导弹的圆概率偏差,σ=CEP/1.177 4。导弹大多散布在靶平面上以T′为中心,3σ为半径的圆内,当弹道高低角ω<90°时,弹道误差圆在水平面内的投影为椭圆。

假设某一次实弹打靶中,实际弹道与靶平面T′-x0y0的交点P0在坐标系T′-x0y0中的坐标为(X0,Y0),那么(X0,Y0)是二维正态随机变量,该弹道与水平面T′-x1y1的交点P1在坐标系T′-x1y1z1中的坐标为(X1,Y1,0),P1在坐标系T-xyz中的坐标为(X,Y,0),坐标系T′-x1y1z1绕T′-z1轴旋转角度-λ后沿T′-x1平移-R得到坐标系T-xyz,有:

(15)

(16)

导弹末段弹道方程由靶平面内的制导偏差(X0,Y0)、方位角λ和高低角ω决定,导弹末端弹道设计为灌顶攻击,即有λ～[0,2π),ω～(0,π/2],导弹的随机弹道方向向量J可以表示为:

J=[-cosωcosλ,-cosωsinλ,-sinω]T

(17)

因此,在坐标系T-xyz中,该弹道方程为:

(18)

3.2 反辐射导弹对目标命中判读

令目标雷达天线馈源点到舰艇甲板的高度为h,天线馈源点在甲板上的投影点到左舷的距离为dL,右舷的距离为dR,舰艏的距离为dH,舰艉的距离为dT。随机弹道与甲板平面交点M′(xm,ym,zm)在坐标系Txyz中的坐标

(19)

导弹与水面舰艇的弹目交会情况在水平面T-xy内的投影如图3所示。

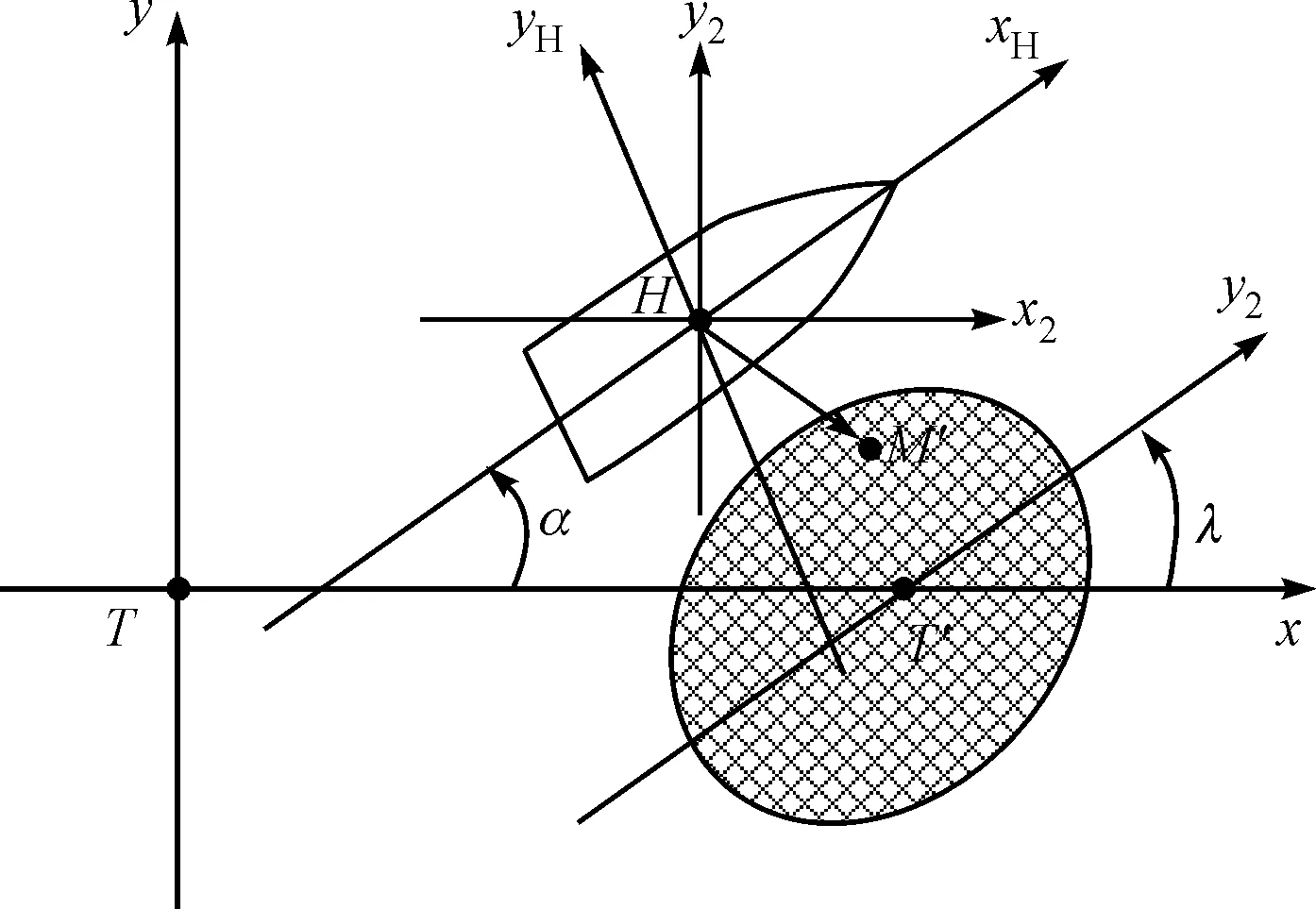
图3 弹目交会示意图

图3中α为弹目交会时目标舰艇的航向角,H-xHyH为舰体坐标系,HxH轴为舰艏方向,HyH指向左舷,忽略漂移角β,HxH与Tx轴夹角为航向角α。H-x2y2为初始航向坐标系,Hx2轴指向关机时刻目标航向,即Hx2和Hy2轴分别与Tx和Ty轴平行。M′在初始航向坐标系H-x2y2中的坐标为:

(20)

坐标系H-x2y2旋转α角得到H-xHyH,M′在舰体坐标系H-xHyH中的坐标为(xmH,ymH)。

(21)

一般大型舰艇都有较厚装甲,而ARM杀伤半径是针对雷达而言的,ARM在甲板以外的位置爆炸对目标破坏作用有限,因此只有炸点在甲板上才被认为是成功命中,命中条件:

(22)

4 导弹对目标命中仿真

4.1 关机距离对命中概率的影响

以反辐射导弹攻击某型驱逐舰上靠近舰艏的雷达为例,通过蒙特卡洛法仿真ARM对机动关机目标的命中情况,雷达高度h=18 m,到左舷的距离dL=10.2 m,右舷距离dR=10.2 m,舰艏距离dH=56.3 m,舰艉距离dT=97.7 m。目标舰长L=155 m,操纵性指数T′=K′=2,由正舵转舵至δ0=35°需要时间t1=10 s,转弯降速比k=0.7,关机时船速VT=10 kn,20 kn,30 kn,40 kn,最大船速Vmax=40 kn。根据ARM被动雷达测角误差和卡尔曼滤波误差,令导弹对目标航向估计误差的标准差σθ=1°,航速估计误差标准差σV=1.67 kn。导弹速度VM=1 000 m/s,导弹制导误差的标准差σ=3 m,末端弹道高低角ω=70°,方位角λ=45°,随机产生10万次导弹和目标的终点位置后统计命中概率,命中概率和关机距离的关系如图4所示。

图4 关机距离对命中概率影响

相同关机距离上目标速度越高命中概率越低。关机距离在20 km以内,目标尚在近似直线运动段,命中概率在70%以上。关机距离在20 km至40 km,目标的机动转弯使得导弹命中概率迅速下降。关机距离大于50 km,命中概率降至10%以下。

设定目标速度VT=30 kn,弹道高低角ω=50°,方位角λ=45°,其它条件不变,仿真300次,关机距离分别为20 km和50 km时目标雷达中心和导弹散布情况如图5和图6所示。

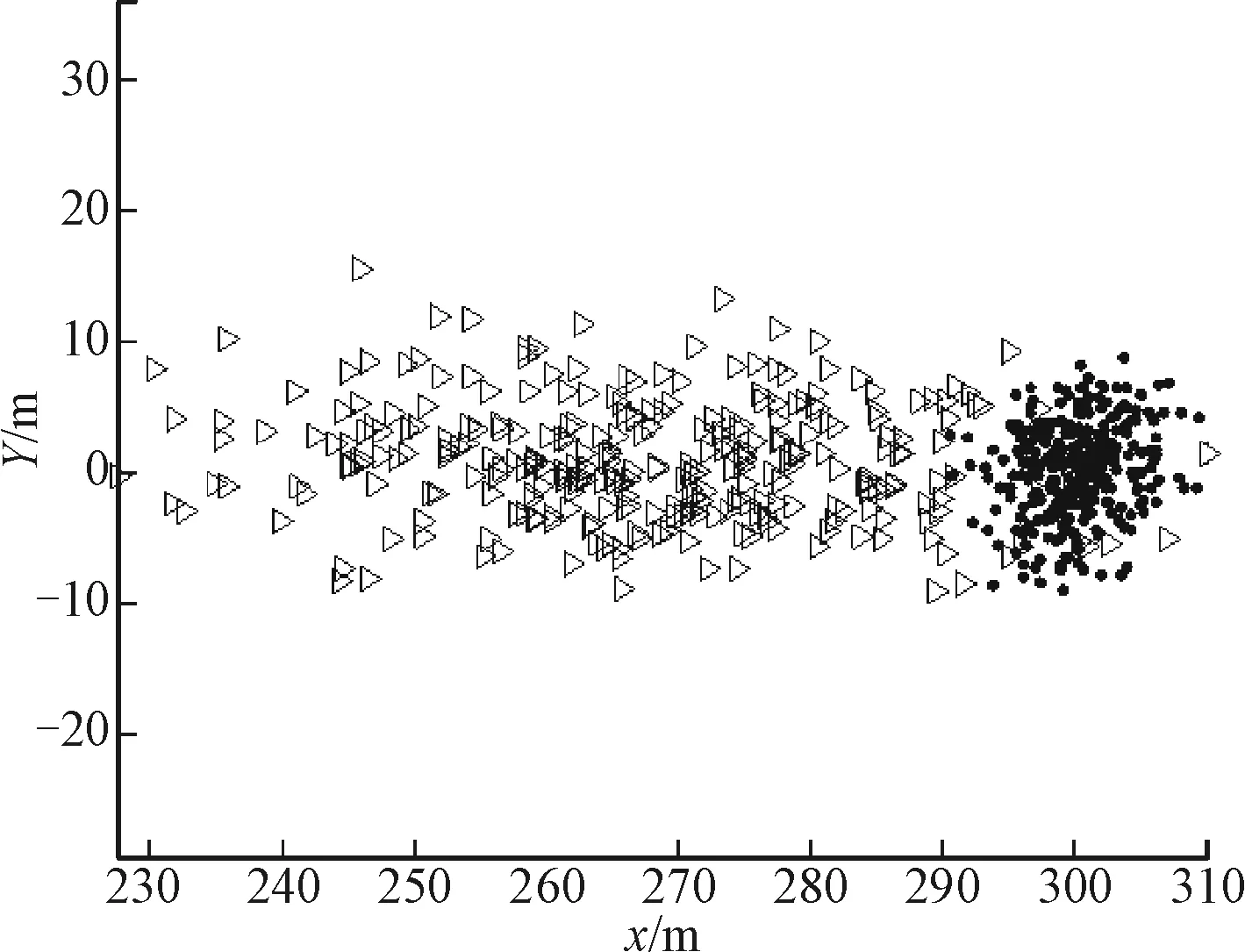
图5 弹目散布位置(20 km)

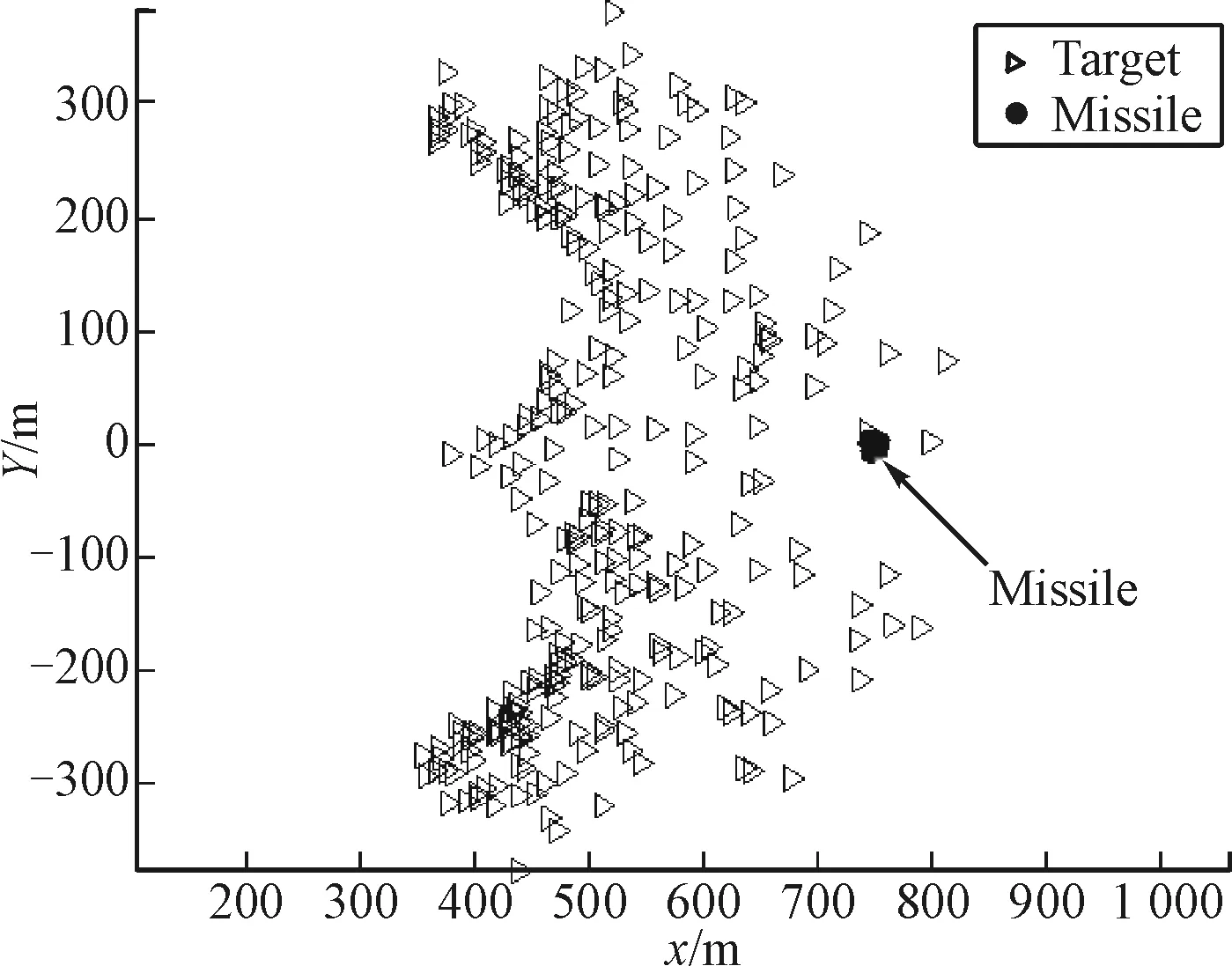
图6 弹目散布位置(50 km)

图5中,目标在20 km距离上才开始准备关机对抗ARM,目标转舵后来不及进入旋回圈,惯性使得目标仍然直线运动,导弹对目标航向和航速的估计误差使目标成长条型散布,转舵造成水阻力的增加降低了目标速度,目标的散布中心落后于导弹,弹目散布面积重合很少,但考虑目标舰艇尺寸的命中概率依然很高。

图6中,50 km距离足够目标进入旋回阶段,目标在原航向两侧的散布范围超过600 m,导弹的散布范围相对来说很小,即使把舰艇尺寸计算在内,也难命中目标。

4.2 弹道入射角对命中概率的影响

设定弹道高低角ω=20°,30°,40°,50°,关机距离d=25 km,目标速度VT=30 kn,其它条件不变,命中概率和弹道方位角的关系如图7所示。

末端弹道入射方位角一定的情况下,命中概率随着高低角增大而提高,且在方位角接近λ=90°时提高更明显。高低角一定时,命中概率的变化趋势随方位角呈U型,方位角λ=0°和λ=180°命中概率最高,λ=90°命中概率最低,也就是说追尾和迎头攻击比侧舷攻击更有效,原因是d=25 km的时间内目标还是呈长条形散布,λ=90°时导弹在甲板平面上的散布椭圆长轴方向与目标散布长度方向垂直,两者相交部分面积最小。

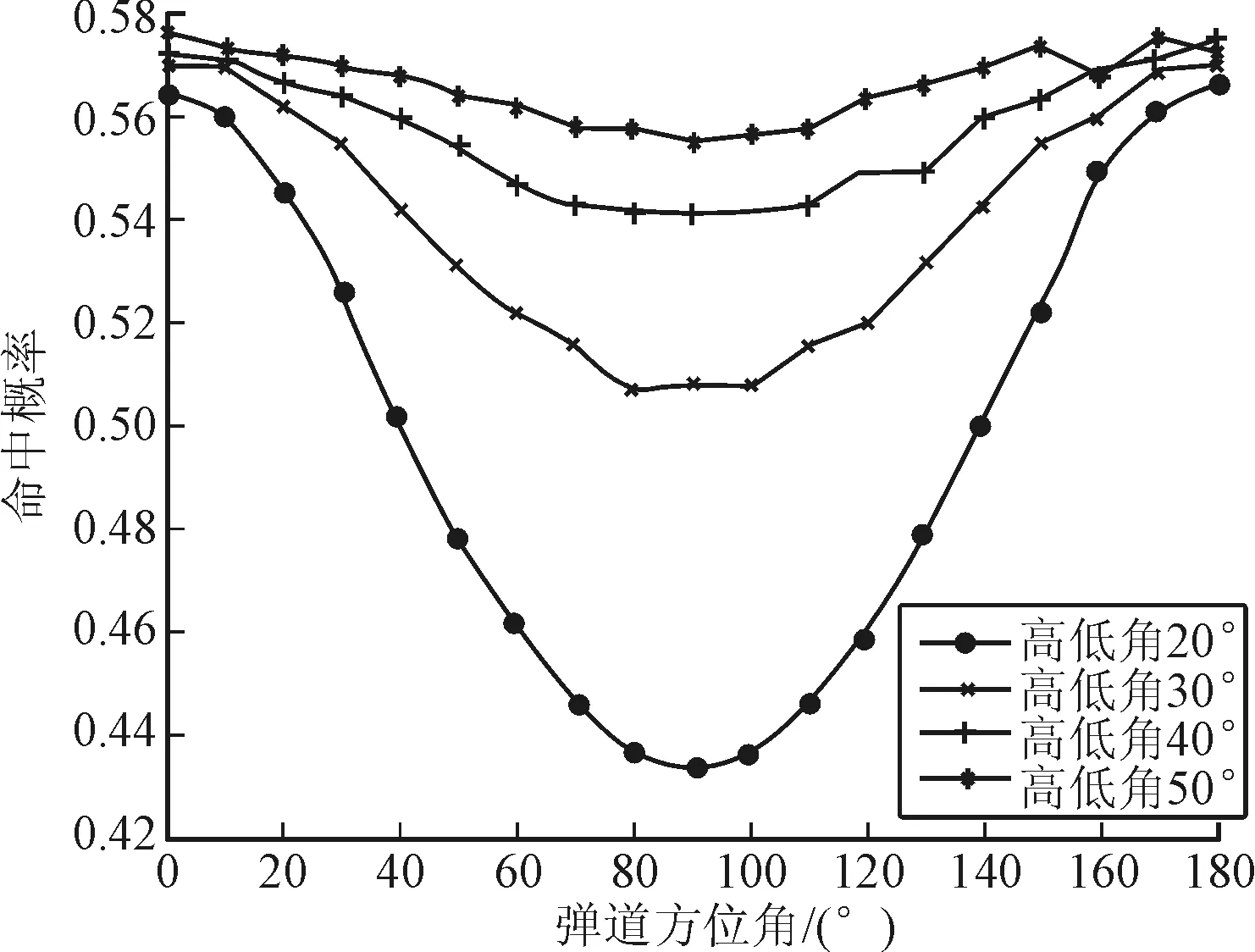
图7 弹道入射角对命中概率影响

5 结束语

仿真结果表明,在关机距离小于20 km(关机时间20 s)的条件下,反辐射导弹具备对机动舰艇目标的有限抗关机能力。主要原因有:反辐射导弹速度高(一般在2Ma以上),目标关机后没有足够的时间进行规避;先进的信息处理技术使得导弹对目标运动有一定的预测能力;高精度卫星导航和惯性导航技术赋予导弹准确飞向预定点的能力;舰艇目标机动能力有限,惯性大导致改变运动状态有时间延迟,速度慢导致机动范围受限;相对于陆基雷达发射车而言,舰艇受弹面积要大的多,这也是增加抗关机可能性的一个重要因素。

另外,可以根据目标的机动散布特性,命中概率和弹道入射角关系,合理组织不同的反舰导弹对高价值目标进行协同攻击,以提高编队的抗关机能力。目标关机期间雷达有源诱饵的诱偏和间歇性关机是下一步重点研究内容。

参考文献:

[1] 汤华, 曲长文. 反辐射导弹抗目标雷达关机方法和能力分析 [J]. 弹箭与制导学报, 2009, 29(1): 260-263.

[2] 谢宇鹏, 严建钢, 武林, 等. 舰载雷达间歇关机对抗反辐射导弹模型研究 [J]. 弹箭与制导学报, 2013, 33(2): 31-33.

[3] 孙凡. 攻击型无人机抗目标雷达关机措施研究 [D]. 西安: 西北工业大学, 2001.

[4] 石利强. 反辐射导弹对移动辐射源的命中概率分析 [D]. 太原: 中北大学, 2008.

[5] 张娟娟, 于云峰, 闫杰, 等. 基于UKF的反辐射导弹抗机动雷达短时关机仿真研究 [J]. 飞行器测控学报, 2010, 29(1): 39-43.

[6] 陈燕. 参数化的渐伸线及应用 [J]. 南京工业职业技术学院学报, 2012, 12(2): 43-46.

[7] 吴秀恒, 刘祖源, 施生达, 等. 船舶操纵性 [M]. 北京: 国防工业出版社, 2005: 14-35.

[8] 章新华, 刘德才, 鄂群. 水声对抗中舰艇规避声自导鱼雷的航速问题 [J]. 兵工学报, 2002, 23(1): 83-85.