内置式永磁电机转子外形对工艺误差的敏感性分析

葛 笑，诸自强,2，陈金涛

(1.广东威灵电机制造有限公司，佛山528311；2.英国谢菲尔德大学，谢菲尔德 S1 3JD)

0 引 言

相比于表贴式架构，内置式永磁电机在某些方面体现出明显的应用优势[1-2]。首先，永磁体可方便地嵌入转子铁心中而无需附加的绑扎措施，在方便生产工艺的同时，也提高了高速运行的可靠性。其次，由于永磁体不直接面对电枢，过载或故障状态下永磁体的抗去磁能力也得到一定程度的提升。此外，利用交/直轴的凸极效应，可产生一定的磁阻转矩，弥补转矩输出能力的不足。因此，内置式永磁电机在工业界和学术界得到了越来越多的重视。

作为永磁电机的一个固有问题，齿槽转矩需要采取特殊的措施加以削弱。内置式永磁电机可以采用转子削弧的方式[3-5]，包括偏心式削弧和正弦式削弧。在不改变永磁体形状的情况下，通过特殊的转子形状可有效降低磁场谐波，进而减小齿槽转矩。此外，为进一步减小齿槽转矩，可以采用转子分段斜极的方式[6]。根据齿槽转矩的基本周期，选择合适的斜极角度，理论上可以到达完全削除的效果。

然而，在电机的量产过程中，工艺误差不可避免，近年来研究人员也开展了大量的工作，研究其对齿槽转矩的影响[7-13]。首先，当电机存在安装偏心时，文献[7-8]应用解析法推导出了不同电机架构中附加齿槽转矩谐波的产生机理。其次，永磁体的非一致性，包括尺寸偏差[9]，形状和位置偏差[10]，充磁效果偏差[11]等，也会引入附加齿槽转矩谐波。文献[12]还采用有限元和磁网路相结合的方法分析了斜极转子轴向偏移的影响。此外，分割铁心技术已广泛应用于分数槽集中绕组电机中以简化绕线工艺，文献[13]表明齿槽转矩的幅值和周期会由于分块定子间的不均匀附加气隙而明显增大。然而，分块定子潜在的安装凸起会影响定子铁心的内圆度，其对齿槽转矩的影响在此前的文献中尚未分析。而且，采用不同转子外形的内置式永磁电机对工艺误差的敏感性差异也需要进一步地明确，以作为电机设计和制造的参考。

本文研究了2种典型的工艺误差对齿槽转矩的影响，并比较了不同转子削弧方法的敏感性差异。以12槽8极电机为例，首先分别建立了偏心式和正弦式削弧的内置式永磁电机模型，并比较了理想状况下的主要性能。针对永磁体不一致性和定子内圆度偏差，分别研究了最敏感的误差分布，并进一步地分析其对2种转子设计齿槽转矩的影响。最后，设计制作了具有不同误差的内置式永磁电机样机，并进行试验验证。

1 内置式永磁电机转子削弧设计

1.1 偏心式和正弦式转子削弧设计

近年来，内置式永磁电机得到越来越多的应用，如车辆系统中的电动助力转向电机、牵引电机和起动发电机等[14-15]。然而，作为电机转矩脉动，噪声与振动的潜在原因之一，齿槽转矩必须采取有效措施加以降低。本节中介绍2种常用的转子削弧方式——偏心式设计(见图1(a))和正弦式设计(见图1(b))。对于偏心式削弧，转子外形由极靴处一系列偏心圆弧(圆心偏离转子中心一个偏心距)和极间处的同心圆弧组成。如图1(a)所示，转子极靴的外径可表示：

(1)

式中：θ为机械角度;A和r分别代表偏心距和偏心圆弧的半径。如图1(b)所示，不同于偏心式转子外形设计，正弦式削弧的极靴可以通过反余弦函数来表示：

Rr(θ)=Rs-δmin/cos(pθ)

(2)

式中：Rs和δmin分别代表定子内经和最小气隙长度;p代表转子极对数。

(a) 偏心式设计

(b) 正弦式设计

1.2 理想情况下不同削弧设计的性能比较

为了衡量2种设计的电机性能，以12槽8极电机为例，按照表1的基本参数，建立了偏心式和正弦式设计的有限元模型。

在上述有限元模型中，除共用同一定子外，2种转子设计的最大与最小外径保持相同,如图2所示，永磁体位置和参数亦保持一致。

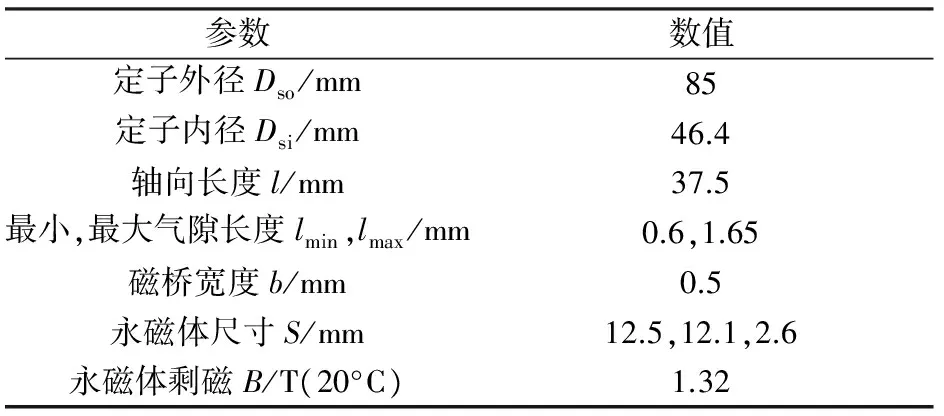
表1 12槽8极内置式永磁电机主要参数

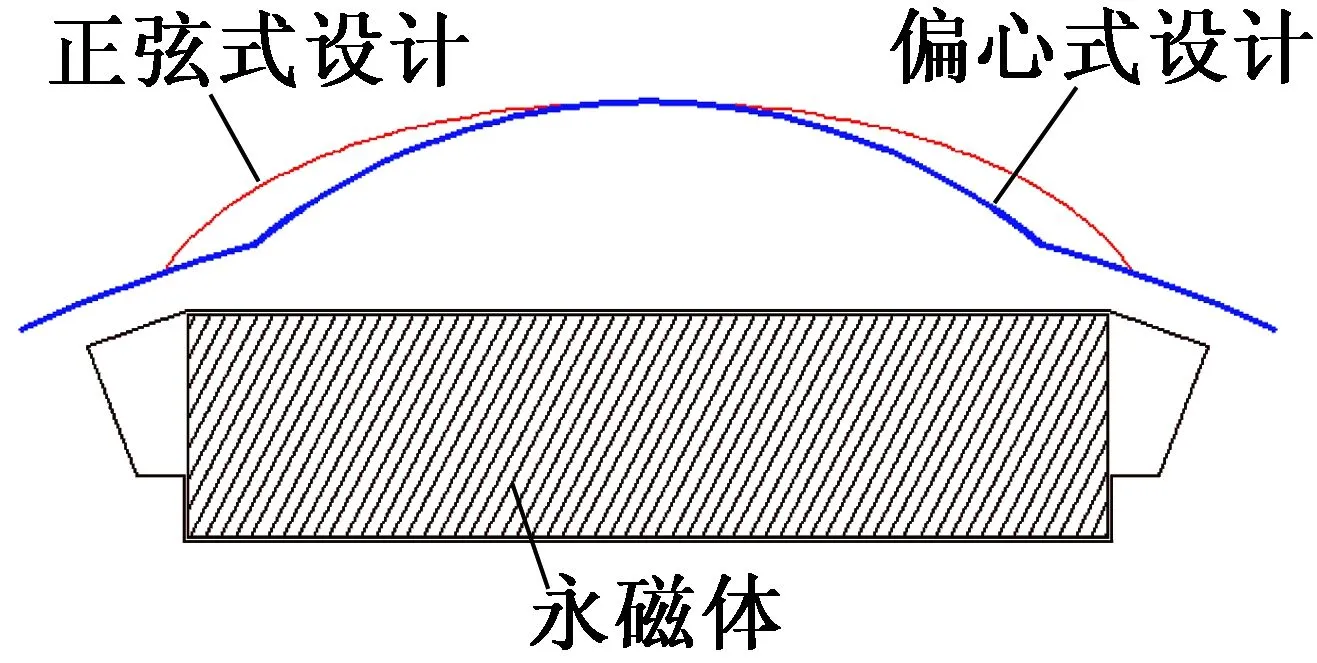
图2 不同转子削弧设计的转子外形对比

借助有限元方法，分别计算出理想情况下2种设计的齿槽转矩(见图3(a))和电磁转矩(见图3(b))性能。可见，偏心式设计在齿槽转矩中引入了明显的24次谐波(±144 mN·m)。对于正弦式设计来说，24次齿槽转矩得到很大程度的削弱(±4.8 mN·m)，同时又引入了±9.6 mN·m的48次谐波。然而理论上，24次和48次齿槽转矩谐波均可通过分段斜极方式得以削除，如三段式转子斜极(分别斜5°,0°和-5°)。此外，从电磁转矩性能可以看出，2种设计的平均转矩基本相同，转矩脉动亦可通过分段斜极的方式降低到较低的水平(<2%)。所以，理想情况下，偏心式和正弦式设计通过转子分段斜极均可得到良好的齿槽转矩和负载转矩性能。

(a) 齿槽转矩

(b) 负载转矩

2 工艺误差对齿槽转矩影响的比较

从上述分析可以看出，借助转子分段斜极，偏心式和正弦式设计在理想情况下均可获得良好的齿槽转矩性能。然而在永磁电机生产过程中，工艺误差不可避免。本节就定转子制造过程中的2种典型工艺误差，进一步分析其对齿槽转矩的影响。

2.1 永磁体不一致性

齿槽转矩和气隙磁场密切相关，然而在永磁体的生产和充磁过程中，永磁体一致性很难保证，如尺寸误差和磁性能偏差无法避免。以N45SH牌号为例，常温下平均剩磁为1.32 T，最高值可达1.42 T(剩磁为该值的永磁体称为非正常永磁体)。

在12槽8极电机中，任一块永磁体出现磁性能偏差时，均会在齿槽转矩中引入12次的附加齿槽转矩分量。根据相邻磁极间的机械角度(45°)和附加齿槽转矩分量的次数(12次)，各非正常永磁体产生的附加齿槽转矩可用向量图来表示,如图4所示。不难发现，不同的非正常永磁体排布对齿槽转矩的影响亦不相同。4块非正常永磁体间隔排布时，会在12槽8极电机中引入最大的12次附加齿槽转矩分量，4倍于单一非正常永磁体产生的附加分量。

图4 12槽8极电机非理想永磁体导致的12次附加齿槽转矩向量图

针对非正常永磁体最敏感的排布，应用有限元方法分别计算出前述偏心式和正弦式设计的齿槽转矩,如图5所示。由于24次和48次的固有齿槽转矩分量均可通过传统的分段斜极方式削除，因此重点关注低阶次的附加分量。如图5所示，偏心式设计中引入的12次附加分量(27.9 mN·m)远高于正弦式设计(12.3 mN·m)。可见，偏心式设计对永磁体不一致性更加敏感，引入的附加齿槽转矩分量更高。

(a) 波形

(b) 谐波成分

2.2 定子内圆度偏差

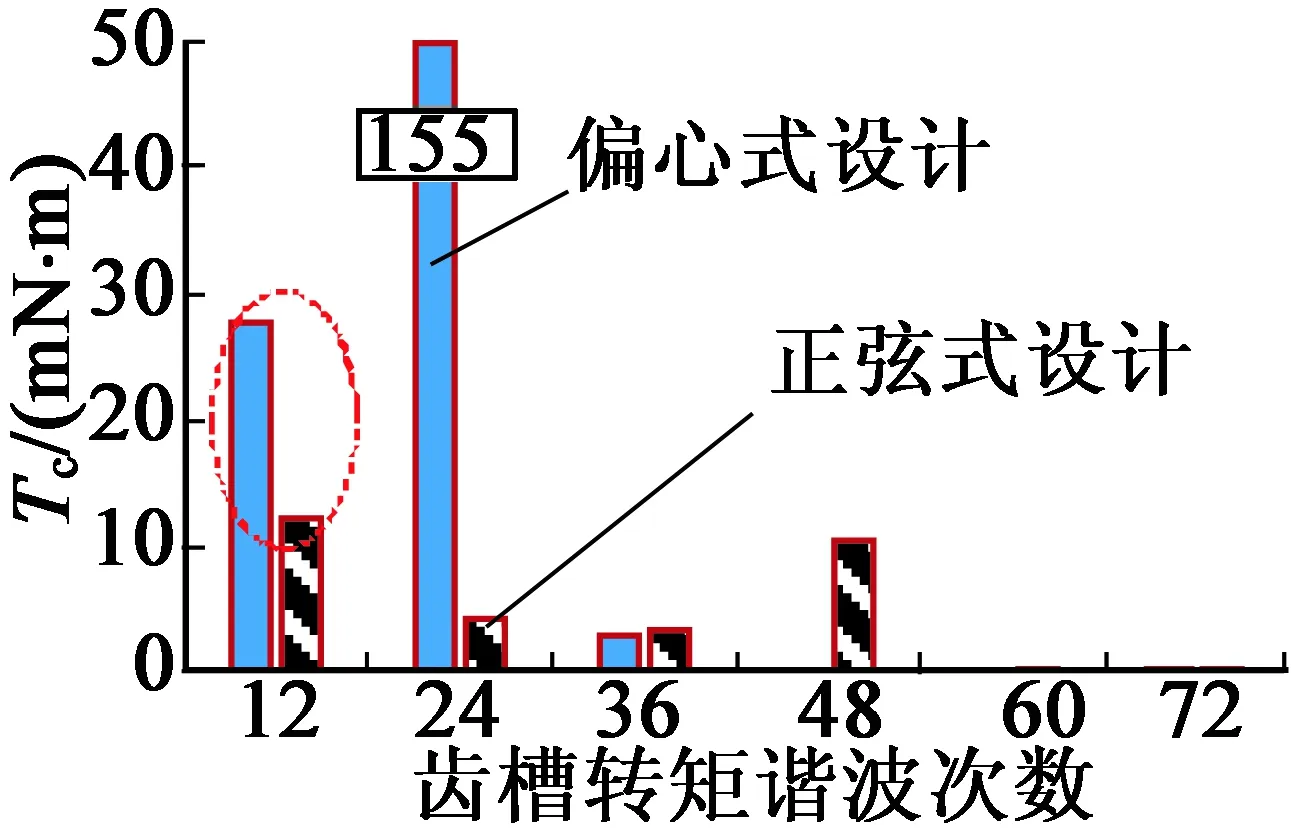
在分数槽集中绕组的永磁电机中，为简化绕线工艺和提高槽满率，分割铁心技术的应用日益增加。然而，在分割铁心的拼装过程中，齿安装凸起(如图6所示)往往不可避免，造成了定子铁心内圆度偏差，其对齿槽转矩的影响亦需进一步研究。

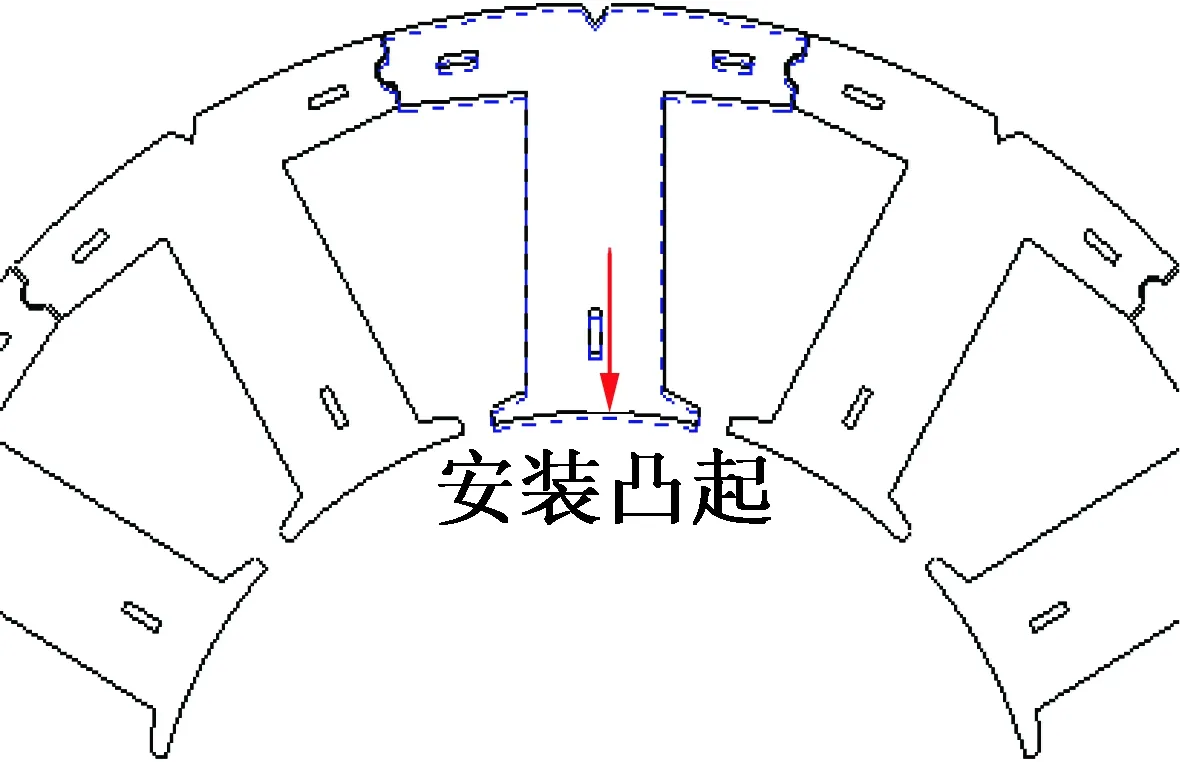
图6 分割铁心中由于齿安装凸起导致的定子内圆度偏差

为明确定子内圆度偏差的最敏感分布，同样可以借助于前述向量图的方法。当12槽8极电机任意一个定子齿存在安装凸起时，均会在齿槽转矩中引入8次的附加分量。根据相邻定子齿之间的机械角度(30°)和附加分量的阶次(8次)，不同定子齿凸起所引入的附加齿槽转矩分量可用如图7所示的向量图表示。不难发现，当同属于某一相的4个定子齿(如1#，4#，7#和10#)存在安装凸起时，引入的8次附加齿槽转矩分量达到最大值，4倍于单一定子齿凸起所引入的附加分量。

图7 12槽8极电机中由齿安装凸起导致的8次附加齿槽转矩向量图

基于上述分析，通过有限元方法分别计算出偏心式和正弦式设计在最敏感的定子齿凸起分布下的齿槽转矩，如图8所示。可以看出，定子内圆度偏差在2种设计齿槽转矩中引入了近似的8次附加分量，分别为24.4 mN·m和21.2 mN·m。

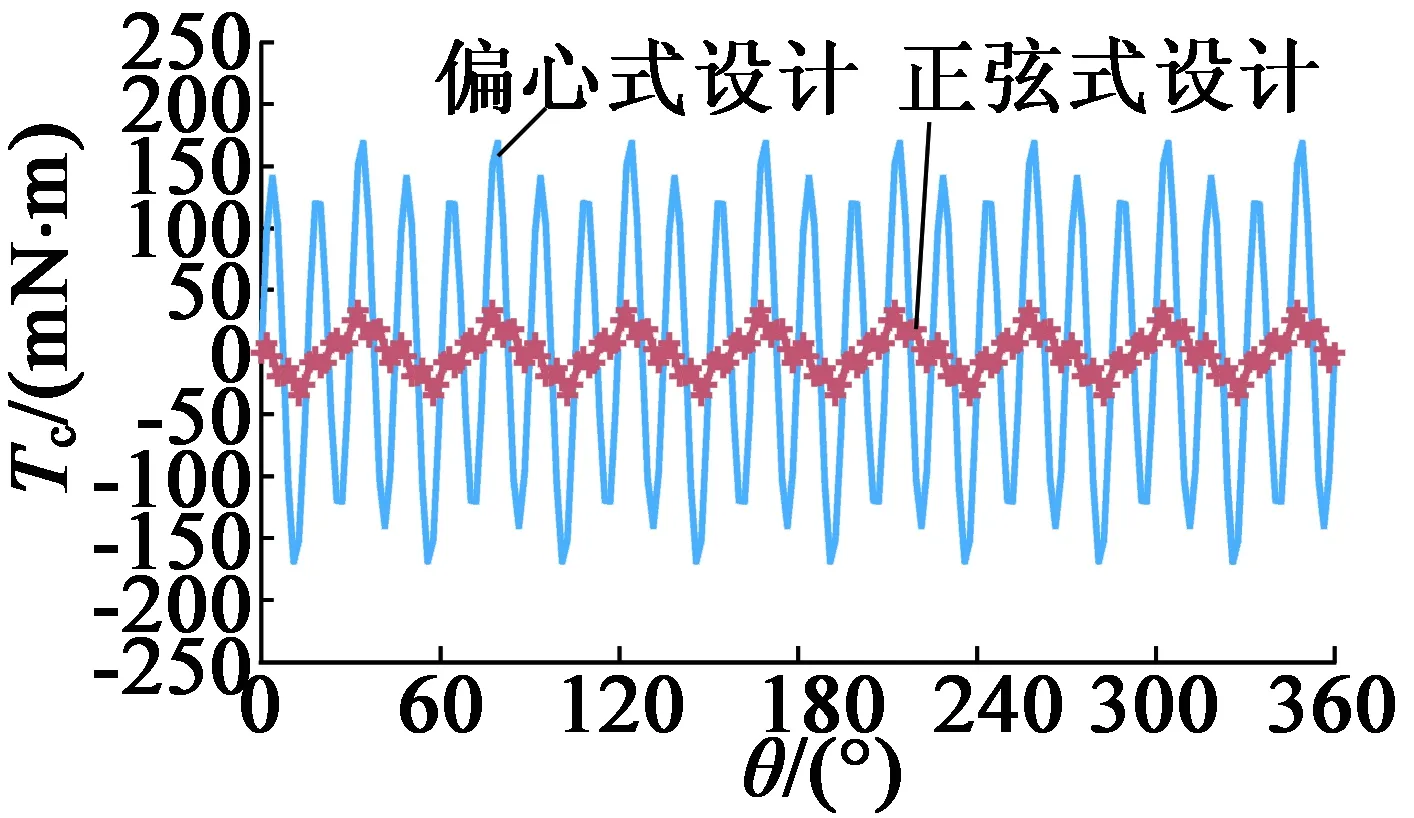
(a)

(b)

3 削弧参数对工艺误差的敏感性分析

在保持最大和最小气隙一致的前提下，上文已经比较了偏心式和正弦式转子削弧方式对工艺误差的敏感性差异。然而，除了最大和最小气隙，偏心式削弧转子之外形亦受制于偏心距。因此，需进一步研究偏心距对上述工艺误差敏感性的影响。保持最大和最小气隙不变，图9(a)反映了偏心距A从12 mm变化到15 mm时转子外形的变化。在前述工艺误差最敏感的分布下，图9(b)为不同偏心距设计附加齿槽转矩分量的变化。

(a) 不同偏心距下的转子形状

(b) 考虑工艺误差后的

可见，当偏心距从12 mm变化到15 mm时，由永磁体不一致性所导致的12次附加齿槽转矩从22 mN·m增加到30.4 mN·m，而由于定子内圆度偏差所导致的8次附加齿槽转矩分量基本保持恒定。因此，选择较小的偏心距在一定程度上可以降低永磁体不一致性的影响，但对定子内圆度偏差的敏感性影响甚微。

4 样机与实验

通过上述分析可以看出，工艺误差存在时，内置式永磁电机齿槽转矩中会引入低阶次的附加齿槽转矩分量，且在不同转子设计中又存在明显的差异。为验证上述分析，基于表1的主要参数，制作了不同设计的12槽8极电机样机，包含理想定子(见图10(a))，带有一个0.2 mm齿凸起的非理想定子(见图10(b))以验证定子内圆度偏差的影响，偏心设计的转子(见图10(c))，以及正弦设计的转子(见图10(d))。另外，验证永磁体不一致性的影响时，转子装设间隔排布的2种牌号永磁体——剩磁为1.32 T烧结钕铁硼和剩磁0.83 T的粘结钕铁硼。为更清晰地呈现低阶次的附加齿槽转矩成分，样机制作过程中转子均采用传统分段斜极(三段，分别为斜-5°，0°，5°)的方式。

(a) 理想定子

(b) 非理想定子

(c) 偏心设计转子

(d) 正弦设计转子

首先，测试了由理想定子(无齿凸起)和理想转子(永磁体均为烧结钕铁硼)组装而成的近似理想样机(如图11所示)。可以看出，理想状况下的齿槽转矩中没有引入明显的低次谐波成分，且2种转子设计其齿槽转矩均在±17 mN·m以内。

(a) 角度为自变量

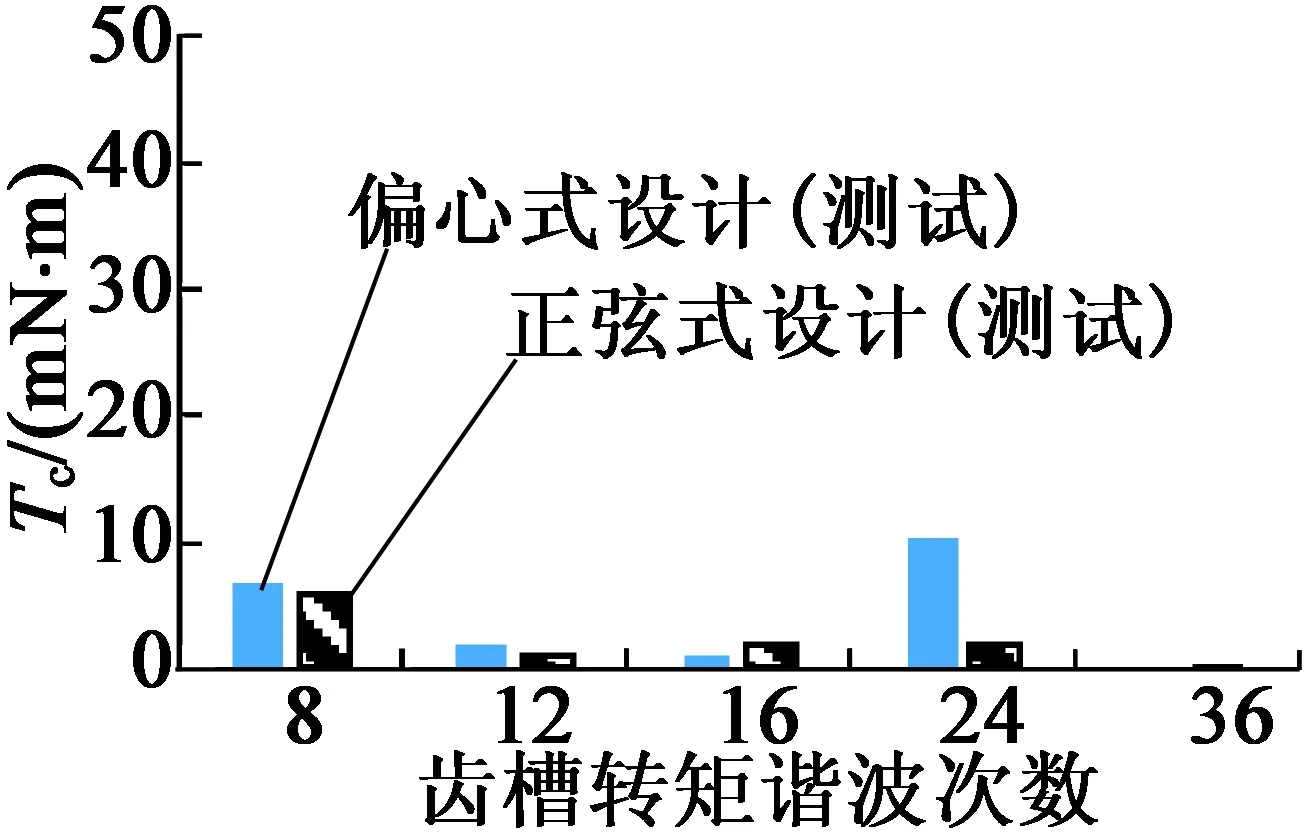
(b) 谐波次数为自变量

转子采用间隔排布的2种永磁体，且共用上述理想定子，测试出2种设计的齿槽转矩。图12表明偏心式和正弦式设计中均引入了明显的12次附加谐波成分，幅值分别为60 mN·m和31 mN·m。因此，偏心式设计的齿槽转矩对于永磁体不一致性更加敏感，与前文的分析结果相吻合。

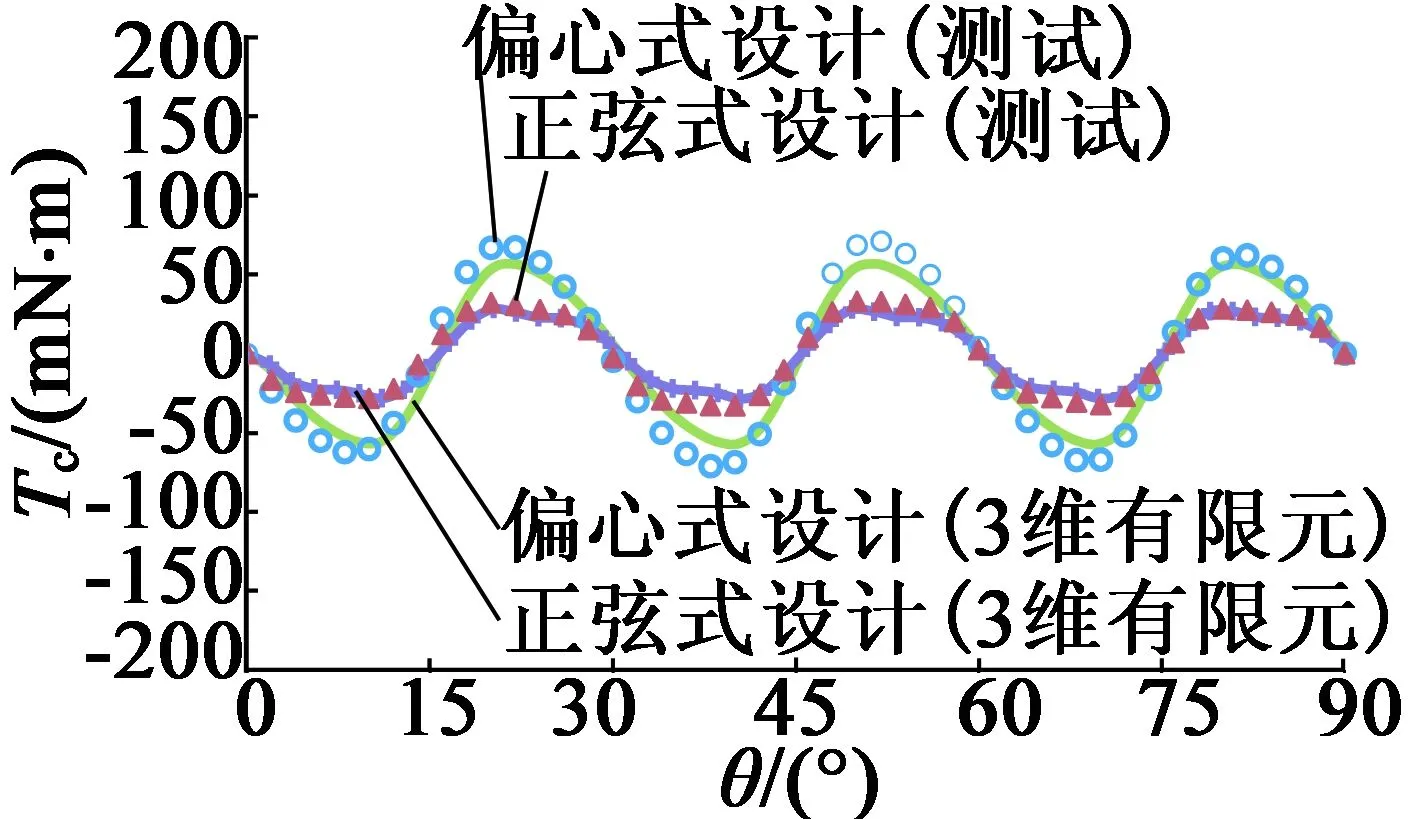
(a) 角度为自变量

(b) 谐波次数为自变量

此外，借助图10(b)所示的具有齿凸起的非理想定子(转子均为理想转子)，验证定子内圆度偏差对齿槽转矩的影响，如图13所示。测试结果表明，齿槽转矩中引入了明显的8次附加谐波成分，且幅值上2种转子设计基本相当。因此，偏心式和正弦式设计对定子内圆度偏差的敏感性并无显著差别。

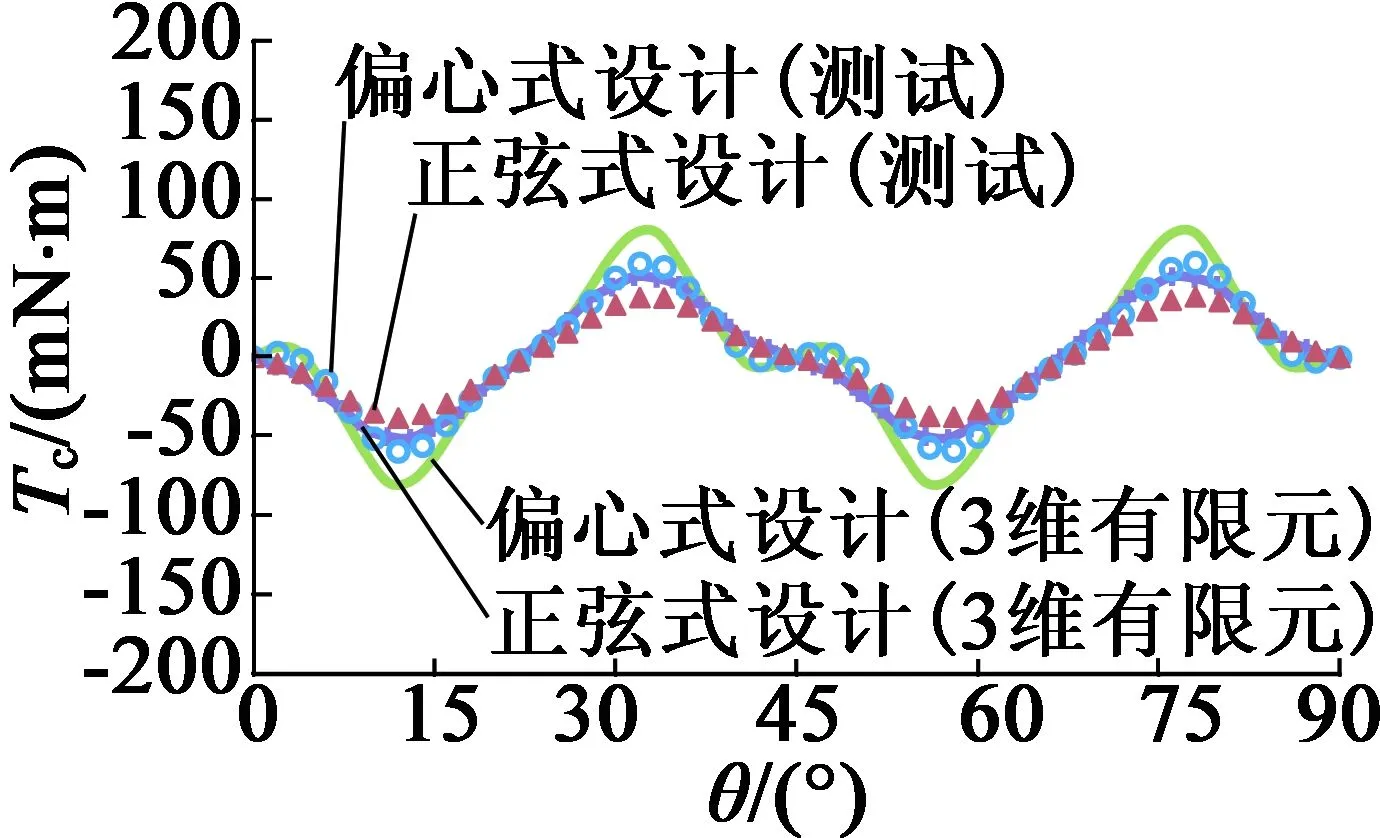
(a) 角度为自变量

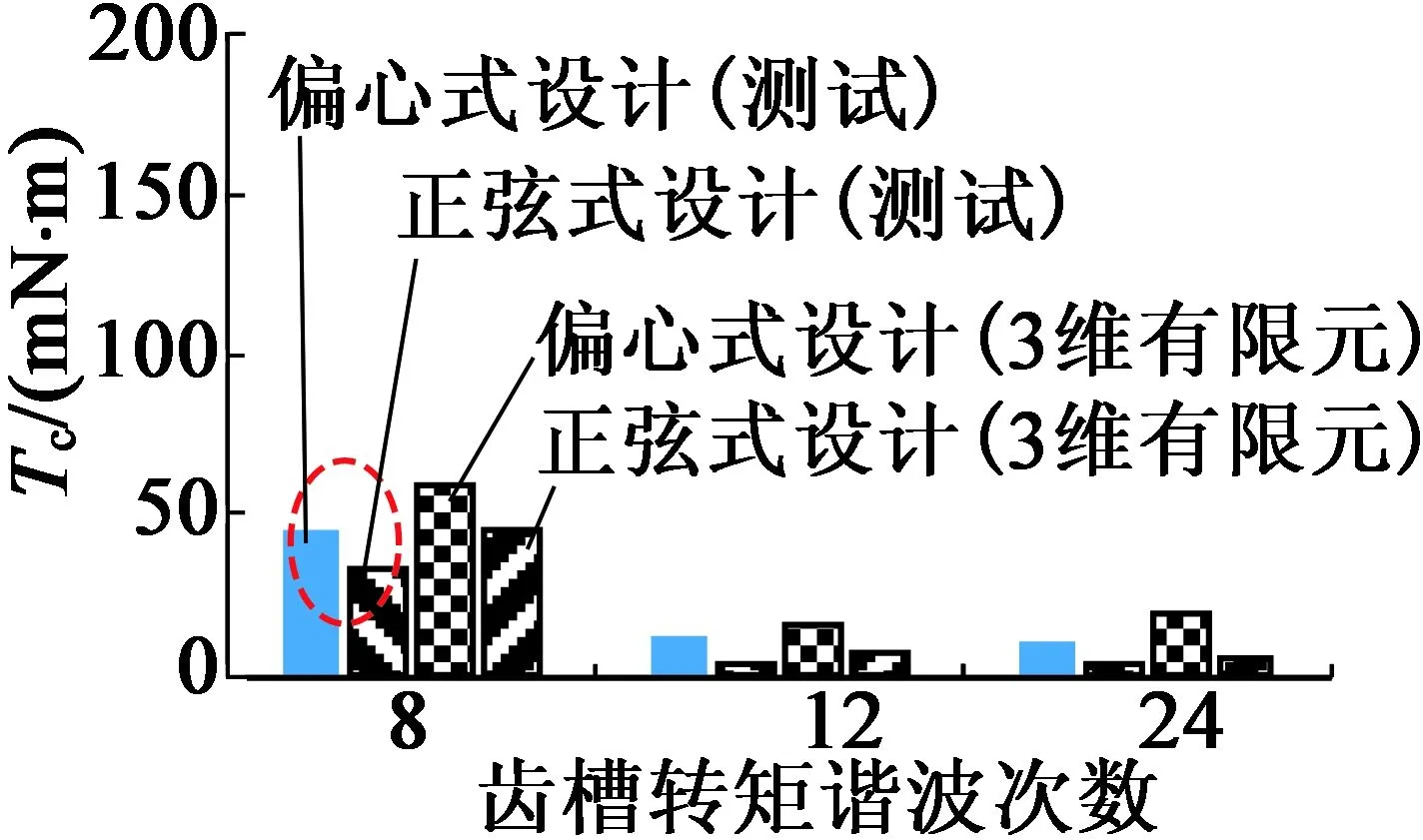
(b) 谐波次数为自变量

尽管电机实际生产过程中永磁体不一致性和定子内圆度偏差不会如此明显，然而本试验通过构造放大的工艺误差方便快捷地验证了其对齿槽转矩的影响，以及不同转子设计的敏感性差异。由于低阶次的附加齿槽转矩成分不能通过传统的分段斜极方式削除，因此，上述工艺误差应该控制在合理的范围内，尽可能地避免敏感的误差分布。

5 结 语

针对内置式永磁电机的不同转子外形设计，本文分析比较了生产过程中的工艺误差对齿槽转矩的影响。以12槽8极电机为例，永磁体不一致性(最敏感分布：间隔排布的非理想永磁体)在偏心式设计中引入更高的12次附加齿槽转矩谐波。此外，偏心式设计和正弦式设计均对定子内圆度偏差较为敏感(特别是当同一相的4个定子齿存在安装凸起时)，在齿槽转矩中引入的8次附加谐波成分基本相当。

[1] REDDY P B,EL-REFAIE A M,HUH K K,et al.Comparison of interior and surface PM machines equipped with fractional-slot concentrated windings for hybrid traction applications[J].IEEE Transactions on Energy Conversion,2012,27(3):593-602.

[2] TINAZZI F,ZIGLIOTTO M.Torque estimation in high-efficiency IPM synchronous motor drives[J].IIEEE Transactions on Energy Conversion,2015,30(3):983-990.

时，Ta=107.19 ，Tr=6.696。与表5中仿真结果相符合。

从表6可看出优化后电机转矩Ta增大了28%，转矩波动Tr和Tr/Ta减小为初始值的87%和68%，电机性能改善明显。

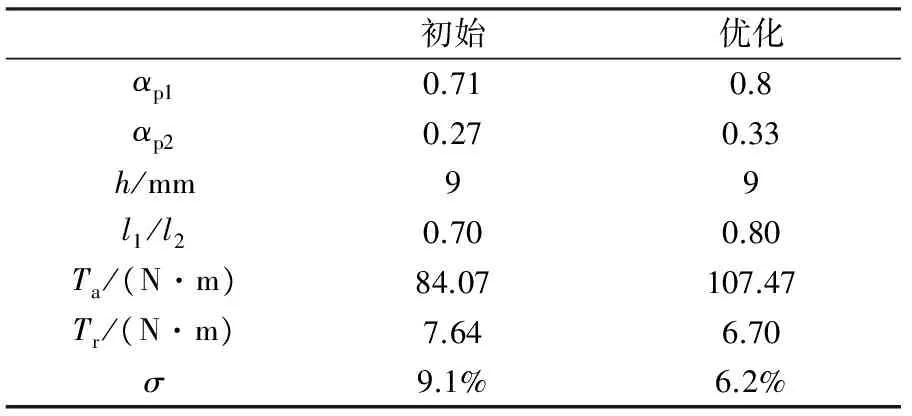
表6 优化前后电机性能对比

3 结 语

本文将田口方法、响应曲面法和遗传算法相结合，针对双层内嵌永磁同步电动机以平均转矩最大，转矩波动最小为优化目标，得到了永磁体埋入位置及永磁体尺寸的最佳组合，简化了电机的优化过程，优化后电机性能获得明显提升，证明了该方法的有效性正确性。

[1] BIANCHI N，Padova Univ, BOLOGNANI S.Design techniques for reducing the cogging torque in surface-mounted PM motors[J].Industry Applications,2002,38(5):1259-1265.

[2] KANO Y，KASAKA T,MATSUI N,et al.A new technique of torque ripple reduction in saliency-based sensorless drive IPM motors for general industrial applications[C]//European Conference on Power Electricnics and Applications.IEEE,2009:1-10.

[3] HUR G K J.Analytical prediction and reduction of the cogging torque in interior permanent magnet motor[C]//IEEE International Conference on Electric Machines and Drives.IEEE,2005.1620-1624.

[4] Zhu Z Q,RUANGSINCHAIWANICH S,SCHOFIELD N,et al.Reduction of cogging torque in interior-magnet brushless machines[J].IEEE Transactions on Magnetics,2003,39(5):3238-3240.

[5] KIM Sung-Il,LEE Ji-Young,KIM Young-Kyoun,et al.Optimization for reduction of torque ripple in interior permanent magnet motor by using the Taguchi method[J].IEEE Transactions on Magnetics,2005,41(5):1796-1799.

[6] IM Young-Hun,HWANG Seon-Ik,JANG Seok-Myeong,,et al.Analysis of torque pulsation considering interior permanent magnet rotor Rib shape using response surface methodology[J].IEEE Transactions on Magnetics,2012,48(2):979-982.

[7] WEN Cheng,YU Haitao,HONG Tianqi.Coil shape optimization for superconducting wind turbine generator using response surface methodology and particle swarm optimization[J].IEEE Transactions on Applied Superconductivity,2014,24(3):1-4.

[8] SOORIYAKUMAR G,PERRYMAN R,DODDS S J.Design optimization of permanent magnet motors using responsesurface methodology and genetic algorithms[C]//Universities Power Engineering Conference (UPEC),2010:1-6.

[9] 虞毅,刘剑峰,鲍军芳.永磁同步电动机转矩的最优化设计[J].航空精密制造技术,2013(4):30-33.

[10] 闵亚能.实验设计(DOE)应用指南[M].北京：机械工业出版社,2011:336-350.