融合小波分解和模糊推理的异步电机转矩控制方案

王 越

(贵州交通职业技术学院，贵阳 550001)

0 引 言

异步电机(以下简称AM)具备自由变速控制、耐用性、少维护、低成本、可靠性等优点，在工业领域广泛应用[1]。目前，AM的控制架构主要分为磁场定向控制(以下简称FOC)和直接转矩控制(以下简称DTC)[2]。这些控制架构中的转矩控制通常采用比例积分微分(以下简称PID)控制器[3]，转矩直接影响电机的转速。然而，PID在所有操作条件下的增益值设定不变，不能实现转速的高稳定性，且在复杂的驱动环境下可靠性较低。为此，学者融入了智能技术来克服上述缺点，如神经网络和模糊推理等。神经网络控制器[4]不需要整个系统的分析模型，并具有适应环境变化的能力。然而，其需要大量的训练过程，这增加了计算时间且影响系统的实时性能。模糊推理[5]是一种简单的智能技术，利用模糊逻辑知识来控制动作，即使在系统未定义，甚至参数变化时仍能够获得良好的效果。

小波变换(以下简称WT)[6]是一种用来提取和检测信号频率分量的多分辨率频谱技术。近年来，WT被应用到控制系统以及电机驱动器故障诊断等领域[7]。文献[8]提出一种小波神经网络控制器进行AM的转矩控制，具有一定的有效性。文献[9]利用小波分析对FOC AM驱动的转子时间常数进行估计，比传统滤波器表现出更好的性能。

FOC中的转矩控制直接影响电机的速度，为了实现电机速度的精确控制，本文首次将WT应用到AM的驱动控制中，并结合模糊推理构建一种应用于由电压源逆变器(以下简称VSI)供电的FOC AM的转矩控制方案。实验结果表明，提出的方案具有良好的可行性和可靠性。该方案的主要创新点在于：

1) 利用2层离散小波变换(以下简称DWT)对电机速度差信号进行分解，获得对应于不同频率的细节分量和近似分量。

2) 利用模糊推理技术处理速度差信号，产生对应于各细节和近似分量的比例增益，用来调整各分量的比重，以此降低环境噪声的干扰。

3) 将缩放增益与相应的小波分量相乘，产生FOC的转矩控制信号，从而控制电机速度。

1 异步电机的FOC模型

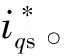
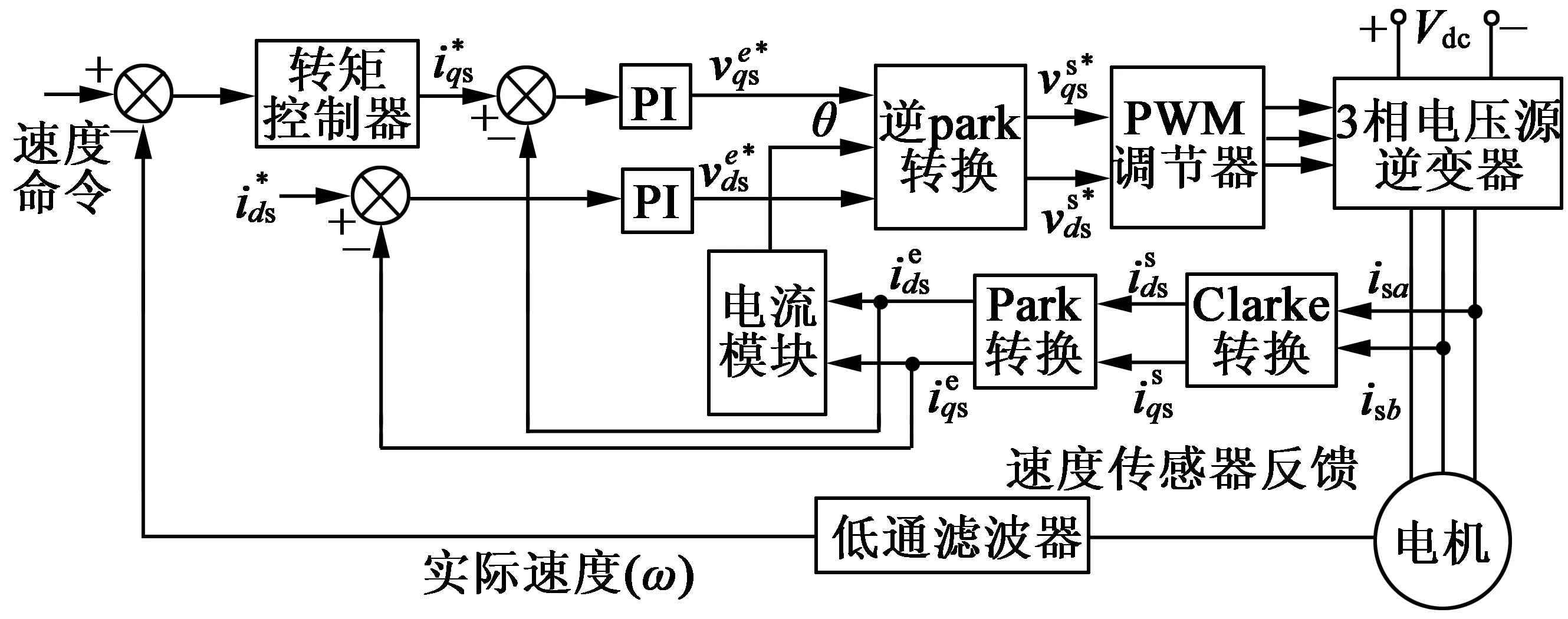
图1 AM的FOC框架

2 离散小波变换(DWT)

WT是在时域和频域上处理和分析给定信号的快速算法。WT的信号数学表示如下[10]：

(1)

式中:s>0表示窗口的大小，决定了梯度小波函数库ψ(t-τ/s)在时间-频率域上的分辨率，且其值反向依赖于频率。信号x(t)的DWT可写：

(2)

式中:ψ*(t)为小波函数，m为扩张表示，n为平移参数。DWT通过低通滤波器(LPF)和高通滤波器(HPF)的级联实现，通过下采样执行频率扩张。LPF的输出为第一层分解的近似信号系数，由a1表示。HPF的输出为第一层分解的细节信号系数，由d1表示。系数a1和d1构成第一层分解，表示：

(3)

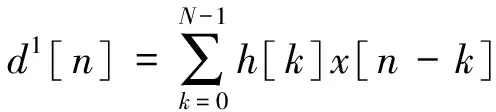
(4)

经过系数为2的下采样后，将第一层分解过程中的近似系数a1作为第二层滤波器的输入。第二层LPF和HPF产生第二层信号系数a2和d2，长度为N/2。第二层分解表示：

(5)

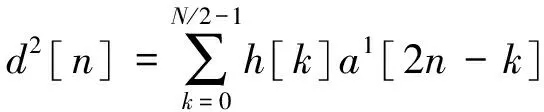
(6)

注意，滤波和下采样过程一直持续，直到达到所期望的层。

3 提出的AM转矩控制方案

3.1 转矩控制总体框架

本文提出的基于小波模糊系统的FOC AM驱动器转矩控制框架,如图2所示。将速度差作为小波模糊系统的输入。首先，利用DWT将速度差信号分解为近似分量(ed1,ed2)和细节分量(ea2)。利用模糊控制器处理速度差信号产生各分量对应的缩放增益(kd1,kd2和ka2)。然后，将缩放增益与相应的小波分量相乘，产生FOC的转矩输入信号，用于控制AM转速。

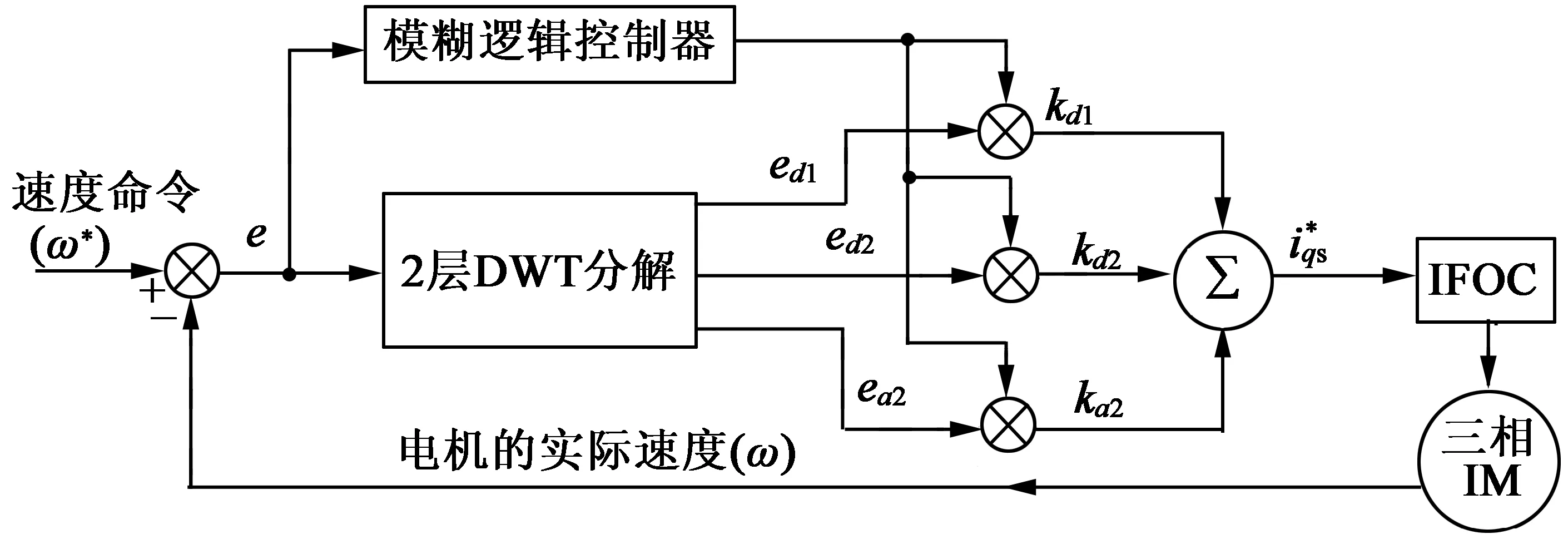
图2 提出的IFOC AM转矩控制方案框架

3.2 小波函数和分解层数的选择

在AM控制系统中，存在着各种频率的物理和电气噪声。反馈控制系统的目的是在每个周期中在排除噪声和破坏性信号下最小化速度差。大多数的数学方法和级数表示都缺乏消除噪声的能力。而基于小波变换的控制器能够判别这些不同频率的信号，以此来解决该问题。

在利用小波时，需要选择合适的小波函数和具有缩放功能的母小波。所期望的小波函数具有紧致、正交、线性相位、低逼近误差等性质。本文利用最小描述长度(以下简称MDL)准则[11]来选择用于信号分解的最佳小波函数。根据MDL准则，一组模式中的最佳模式将拥有数据模型本身的最短描述，定义：

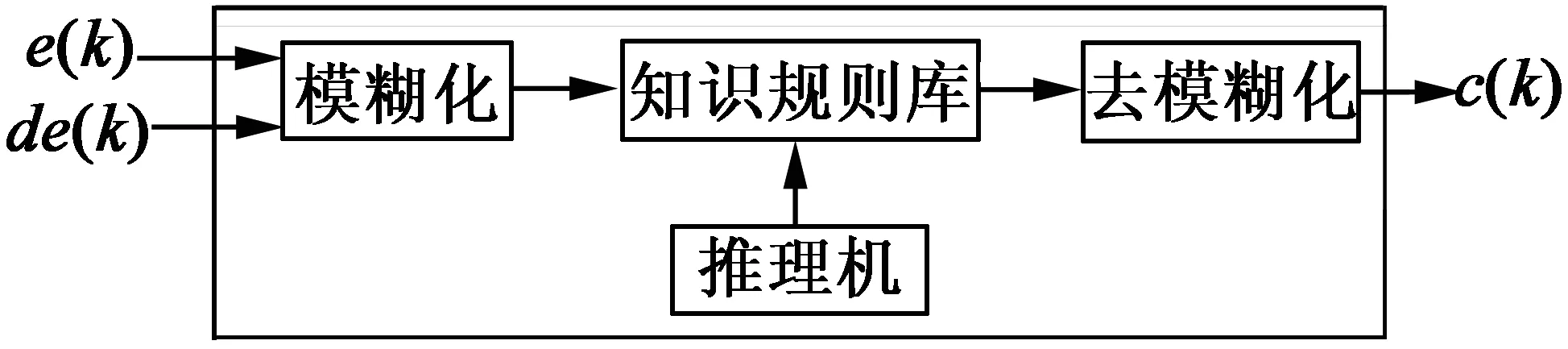
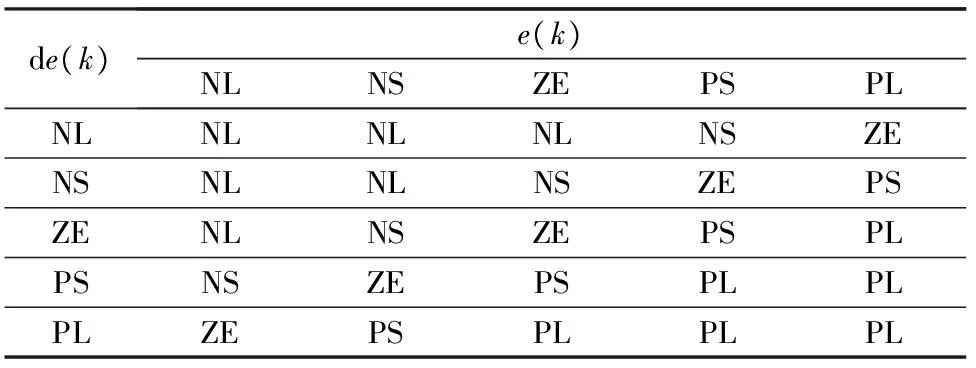
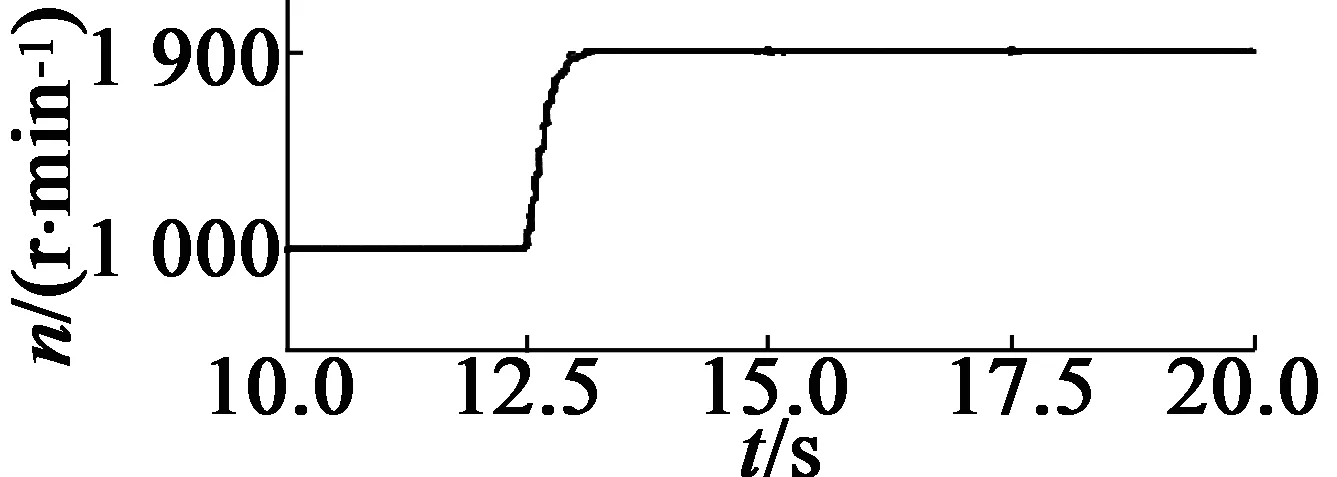
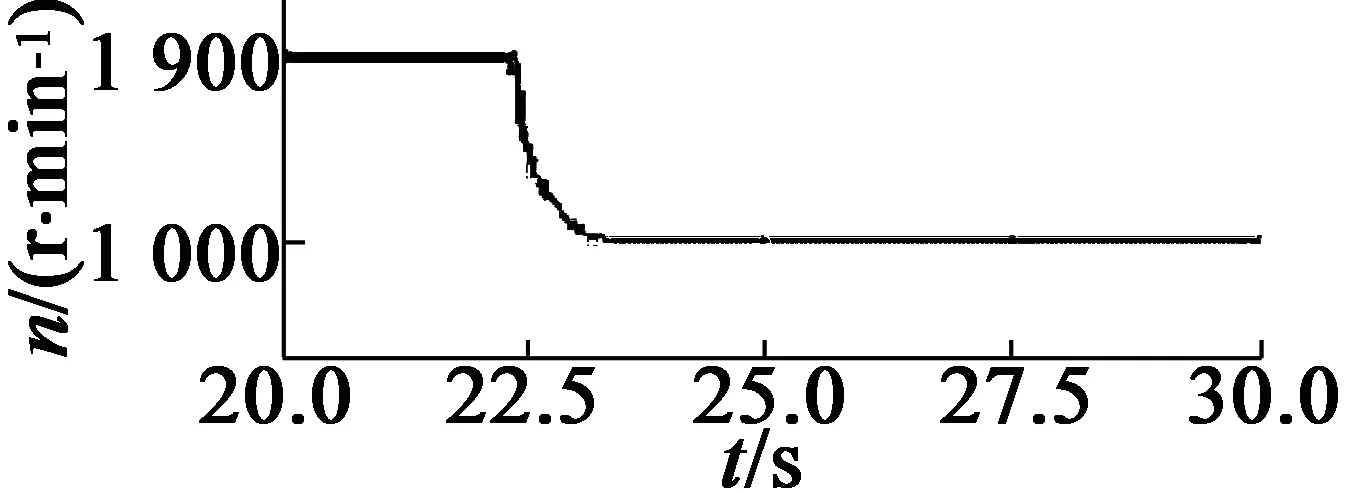
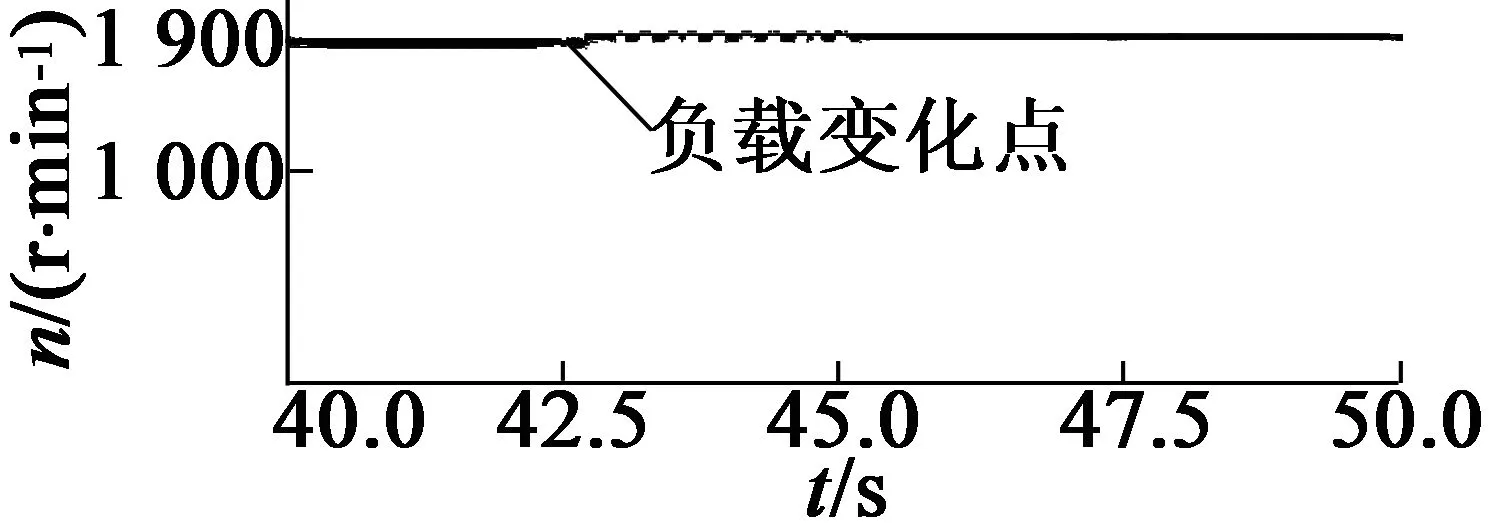
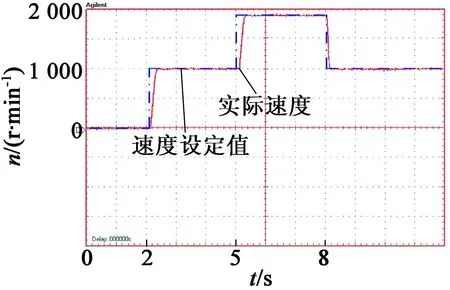
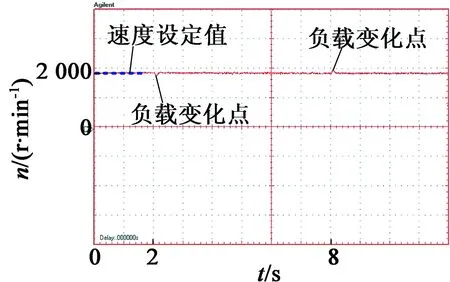
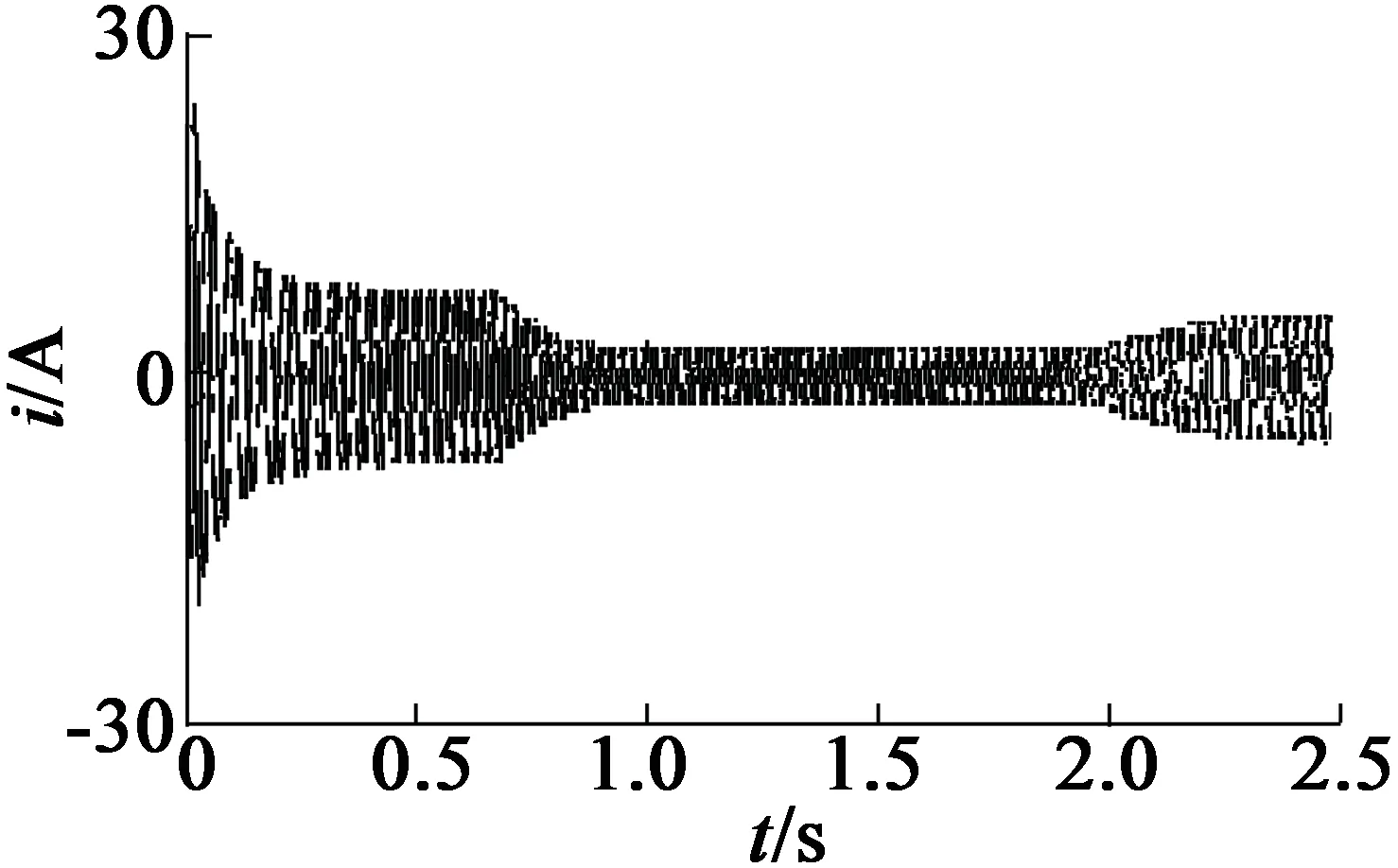
0≤k

(7)

在将速度差信号输入到DWT之前，选择分解层数很重要。分解层数决定了小波控制器所需的调整增益的数量，其取决于用于分解的信号。香农熵准则最适合于确定电机驱动中速度差信号的最佳分解层。信号x(n)的熵可以表示：

(8)

在每一层分解中，为速度差信号的近似和细节分量系数进行熵计算，以此检测分解的最佳层。基于香农熵准则，如果下一层(p)信号的熵比前一层(p-1)的高，即：

H(x)p≥H(x)p-1

( (9)

那么，信号的分解在层(p-1)停止，层(p-1)即为最佳分解层。通过上述分析，2层小波分解足以满足速度差信号的有效表示。

3.3 模糊推理机制

本文利用模糊推理来确定小波分解后各分量的增益系数，以此消除噪声干扰。图3(a)为模糊推理系统的示意图，由模糊化、模糊规则和去模糊化单元组成。模糊推理系统的输入为速度差e(k)和速度差的变化量de(k)(当前速度差与前一时刻速度差之间的差)，相应的隶属函数如图3(b)所示。

(a) 模糊推理系统的结构

(b) 误差e和误差变化量de的隶属函数

首先，模糊推理系统使用给定的三角隶属函数将明确变量e(k),de(k)转换为模糊变量E(k),dE(k)，分为5个模糊集：NL(负-大)，NS(负-小)，ZE(零)，PS(正-小)和PL(正-大)。每个模糊变量为隶属度在0(非成员)到1(全成员)之间变化的子集[12]。

然后，根据表1给定的5×5模糊规则矩阵，由推理机处理模糊变量E(k)和dE(k)。这些规则是基于速度差信号的动态行为而设计，规则的形式如下：If ‘x’ is ‘A’ and ‘y’ is ‘B’ - Then ‘z’ is ‘C’。推理算法用于分离模糊集合值以输出模糊变量 ，本文使用最大-最小推理算法[13]，其中隶属度为E和dE的隶属度中的最大值。

接着，执行去模糊化操作，将推理机的模糊输出变量转换成明确值。这里，本文使用重心去模糊算法，以隶属函数的重心来计算明确值。

表1 模糊逻辑规则矩阵

3.4 转矩控制输出

首先，对速度差信号进行小波变换，以不同级别的分辨率将速度差信号分解为不同频率的细节分量ed1,ed2,…,edN和近似分量eaN。然后，由模糊推理获得用于调整各分量的增益系数：kd1,kd2,…,kdN和kaN。最后，将各分量与增益系数相乘并相加，产生输入到FOC的转矩信号uw，从而控制电机速度。计算如下：

uw=kd1ed1+kd2ed2+…+kdNedN+kaNeaN

(10)

在驱动AM时，命令和扰动信号为低频，传感器噪声为高频。那么，合理调整速度差信号低频分量的增益可用于提高AM的抗扰动能力；而降低高频分量的增益可用于消除噪声信号的影响。各分量根据它们各自的增益缩放，加在一起产生转矩控制信号 u，以此对复杂场景具有鲁棒性。

4 实验及分析

4.1 实验设置

构建实验平台，由PC机、TMS320F2812(DSP)控制板、基于IGBT的PWM逆变器、三相交流AM和信号(电压/电流)测量仪器组成，如图4所示。其中三相AM型号为380V的Y112M-2AM型，额定功率为4kW，额定速度为2 800r/min，额定转矩为13.6N·m，额定电流8.2A，极对数为2。AM的电流由霍尔传感器测量，并通过模拟/数字转换后输入到DSP板中。提出的转矩控制系统在DSP控制板中执行，其输出的数字脉冲通过隔离后触发逆变器的IGBT，从而控制电机。

图4 实验平台

在速度上升时间，上冲下冲情况和控制稳态误差方面评估控制系统性能。利用100MHz带宽、500MS/s采样率的Tektronix信号示波器来测量实际速度。

4.2 仿真分析

首先，利用MATLAB/Simulink软件对本文控制系统进行仿真，以验证控制系统的可行性。

图5为本文控制系统对速度指令的跟随响应。其中，设定在t=12.5s时速度从1 000到1 900r/min逐步增加;在t=22.5s时设定速度从1 900到1 000r/min逐步降低。可以看出，速度曲线能够很好地跟随设定值，大约只需0.5s即可控制到稳态速度，且没有过度调节现象。

图5 速度变化时的速度控制响应曲线(仿真)

为了研究负载对控制系统的影响，仿真中设置电机速度为1 900r/min，在t=32.5s时增加30%的额定负载，在t=42.5s时移除30%的额定负载，观测本文控制系统的稳定性，结果如图6所示。可以看出，负载变化会影响速度的稳定性。但本文控制器能够快速地对速度进行调整并使其稳定，展示了对负载变化良好的鲁棒性。

图6 负载变化时的速度控制曲线(仿真)

4.3 实际实验

在构建的实际实验平台上进行实验。首先，在2N·m负载情况下，验证控制系统对速度变化的响应。其中，在t=2s时设置速度由0变到1 000r/min；在t=5s时设置速度由1 000变到1 900r/min；在t=8s时设置速度由1 900变到1 000r/min。速度控制结果曲线如7所示。可以看出，与仿真结果一样，本文控制系统能够快速且准确的跟随速度设定值。

图7 速度变化时的速度控制响应曲线(实际)

然后，研究负载变化对控制系统的影响。设定电机以1 900r/min的速度恒速运行，待转速稳定后，在t=2s时施加2N·m的负载，在t=8s时移除负载。速度控制曲线如图8所示。可以看出，负载变化对速度的影响很小，控制系统能够很快地调整并稳定速度。

图8 负载变化时的速度控制曲线(实际)

图9给出了电机从起动到t=2s处施加负载时的三相定子电流输出波形。可以看出，起动时的电流很大，约0.7s后电流稳定到正常值。在t=2s处施加负载时，电机电流迅速上升并很快趋于稳定。

图9 添加负载时的电机三相定子电流变化

另外，对上述实验中稳定状态时的速度进行采样，计算速度控制的稳态误差值。通过计算得到，本文控制器在1 000r/min时稳态误差约为16.4r/min，在1 900r/min时稳态误差约为22.1r/min，控制误差在设定速度值的1.5%以内，符合高精度控制要求。而在同样场景下，当设定速度为1 000r/min和1 900r/min时，传统PID控制的稳态误差约为28.5r/min和34.6r/min，明显高于本文方案。

根据上述实验，可以得出结论，提出的FOC中转矩控制器具有有效性，在跟随速度变化时几乎没有过冲现象，且上升时间快、控制精度高、稳定性好。

5 结 语

本文提出了一种用于FOCAM的小波模糊转矩控制器，利用小波分解获得速度差信号的频率分量，利用模糊推理获得各分量的增益，从而在排除噪声干扰下获得转矩控制信号，进而精确控制电机速度。数值仿真和实际实验的结果表明，提出的控制方案对环境噪声和负载变化具有鲁棒性，且控制精度高、无过调节现象，符合工业应用需求。

[1] 万晓凤,朱俊裕,肖京.纯电动汽车三相异步电动机矢量控制[J].微特电机,2012,40(1):61-63.

[2]ZHUJ,WANGX,XUB,etal.Acomparativestudyonfieldorientedcontrolanddirecttorquecontrolforpermanentmagnetlinearsynchronousmotor[J].JournalofComputers,2013,8(1):132-139.

[3] 彭继慎,宋朋磊.改进PID和模糊控制在异步电机DTC中的应用[J].计算机仿真,2014,31(6):329-333.

[4] 许辉,王自强.基于神经网络的有限转角力矩电动机滑模控制[J].微特电机,2015,43(11):39-42.

[5] 朱建渠,张罡.三相异步电机模糊控制的研究[J].电力电子技术,2012,46(7):81-83.

[6] ASFANI D A,MUHAMMAD A K,SYAFARYDDIN,et al.Temporary short circuit detection in induction motor winding using combination of wavelet transform and neural network[J].Expert Systems with Applications,2012,39(5):5367-5375.

[7] 祝洪宇,胡静涛,高雷,等.Morlet小波解调制方法诊断鼠笼电机转子断条故障[J].电机与控制学报,2014,18(7):31-36.

[8] SANJEEVIKUMAR P,DAYA J L F,WHEELER P,et al.Wavelet transform with fuzzy tuning based indirect field oriented speed control of three-phase induction motor drive[C]// International Conference on Electrical Drives and Power Electronics.Slovakia:IEEE,2015:153-158.

[9] FARAHANI M,BIDAKI A R Z,ENSHAEIEH M.Intelligent control of a DC motor using a self-constructing wavelet neural network[J].Systems Science & Control Engineering An Open Access Journal,2014,2(1):261-267.

[10] 王欣,杜阳,周元钧,等.基于小波变换和聚类的BLDCM故障检测与识别[J].北京航空航天大学学报,2014,40(10):1436-1441.

[11] 赵闻蕾,孔莉,王娟娟,等.基于MATLAB和小波变换的电力机车谐波电流分析[J].电力自动化设备,2012,32(1):103-106.

[12] JANIER J B,ZAHARIA M F Z,KARIM S A A.Use of fuzzy inference system for condition monitoring of induction motor[J].Aip Conference Proceedings,2012,14(3):441-445.

[13] RAMADAN E H M,EL-BARDINI M,EL-RABAIE N M,et al.Embedded system based on a real time fuzzy motor speed controller[J].Ain Shams Engineering Journal,2014,5(2):399-409.