基于自适应区域搜索算法的圆度误差评定

龚玉玲，徐晓栋，苏召宁，龚 非

（1.泰州学院 船舶与机电工程学院，泰州 225300；2.中国航天科工集团8511研究所，南京 210007）

基于自适应区域搜索算法的圆度误差评定

龚玉玲1，徐晓栋1，苏召宁1，龚 非2

（1.泰州学院 船舶与机电工程学院，泰州 225300；2.中国航天科工集团8511研究所，南京 210007）

根据圆度误差的几何特征，提出自适应区域搜索算法的圆度评定方法。首先根据待测圆轮廓点坐标确定初始圆心位置，以该圆心为中心确定搜索区域；然后根据自适应区域搜索算法，调节搜索区域，获得全局最优解。通过实例验证，该算法简单直观，易于编程，操作方便。与最小二乘法相比，圆度误差评定精度提高了14.5%，实现了圆度误差的精确评定，具有较好的实际指导意义。

圆度误差；自适应区域搜索；全局最优解

0 引言

圆度误差评定是圆形零件形位误差的一项重要评定指标[1]，其误差反映了实际圆与理想圆之间的变动值，其数值是以包容实际测量点的两个同心圆的半径差表示。圆度误差评定的关键是找出被测圆轮廓的理想圆心位置。其中国标规定的圆度误差评定常用方法为最小二乘法、最小区域法、最大内接圆法和最小外接圆法[2]。最常用的评定方法是最小二乘法，其算法简单且求解唯一，但是该算法有较多限制条件而影响该算法的使用[3]。最小区域法符合国标评定准则，使用较广泛，但是该算法涉及非线性最优化极值求解问题，实现较困难[4,5]。因此国内外学者利用数据分析方法对最小区域圆度误差评定进行研究，如遗传算法[6]，线性化算法[7]，二分法逼近搜索[8]等，这些算法具有一定的实用性，但是这些算法大都较复杂，较难掌握而限制其实际应用。

本文在上述研究的基础上，结合圆度误差的几何特征，提出自适应区域搜索算法的圆度误差评定方法，以实现圆度误差简单快速准确评定的要求。

1 自适应搜索算法原理

自适应搜索是根据圆心位置特点，在一个自适应调节的区域范围内，寻找最佳的圆心位置，以满足最小区域评定要求，具体方法如下。

1.1 初定圆心

首先，在待测圆周上的测量点上Pi(xi,yi)(i=1,2,…,n)，n≥3。任取Pi内三个尽量分散的三点Pu(xu,yu)，Pv(xv,yv)，Pw(xw,yw)，如图1所示。

图1 圆周取点初定圆心图

以三点为边界拟合一个圆，令圆心坐标为O0(x0,y0)，则PuPv的矢量为：(xu-xv,yu-yv)，PuPw的矢量方向为(xu-xw,yu-yw)，圆心到两直线中点的矢量分别为：由

矢量垂直关系，建立圆心方程，有：

1.2 确定搜索区域

以O0(x0,y0)为圆心，lm=Δ为半径(Δ为搜索步长，m为常数)，在2π的圆周内均匀划分区域，假设角度均分为s段，半径均分为r段，则每个搜索点为Pk(xij,yij)的坐标为：

圆度误差评定的目标函数：

约束条件：

计算圆心的目标函数为：

则圆度误差评定结果：

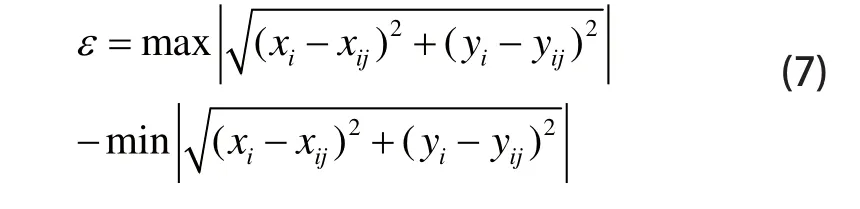
1.3 自适应区域搜索

设定的l半径搜索区域内，按式(3)划分区域搜索，由式(4)计算目标函数fij，当搜索点的目标函数值fij小于圆心的目标函数值f0时，进行缩小区域搜索，反之，进行放大区域搜索。如图2所示。

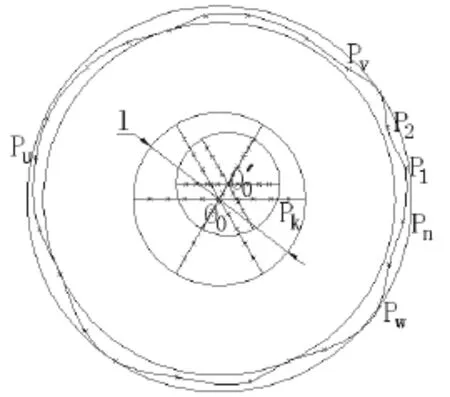
图2 自适应区域搜索示意图

缩小区域搜索半径方程为：

放大区域搜索半径方程为：

根据自适应搜索区域，寻找最优圆心替换圆心O0(x0,y0)，替换方程为：

2 自适应区域搜索算法流程

采用VC 6.0++编程，完成自适应区域搜索算法，算法步骤为：

步骤1：输入圆度测量点Pi，从Pi中选择尽量分散的三点，由式(2)计算初始圆心O0(x0,y0)和半径R；

步骤2：以2lm=Δ为半径的圆区域内，以角度、半径分别均分为s、r段，由式(3)确定搜索点Pk(xij,yij)；

步骤3：计算初始圆心点O0(x0,y0)与搜索点Pk(xij,yij)的目标函数值f0和fk；

步骤4：当f0＞fij，由式(10)，将该处搜索点替换成新的圆心O0，同时采用缩小区域搜索法，半径缩小为：llα′=(1)α＜，重复步骤2和3；当14 le′＜−时搜索结束。

步骤5：当f0≤fij，圆心位置不变，采用放大区域搜索法，半径放大为：重复步骤2和3；当l′＜1e−4时搜索结束。

步骤6：输出最佳圆心点和圆度误差值。

自适应区域搜索流程如图3所示。

图3 自适应区域搜索流程图

3 实例验证

采用接触式三坐标测量机CMM（型号LKG90C）测量某轴承的外圆圆度，均匀采集外圆圆周50个测量点，测量图如图4所示，采集数据如表1所示。

图4 CMM在线测量轴承外圆图

表1 采集圆度坐标值

表2 圆度误差评定

由表2可见，本文所用算法分别与最小二乘法，线性化算法文献[7]，二分法逼近搜索文献[8]进行比对，精度分别提高14.5%，11.5%，13.0%。

4 结论

本文提出自适应区域搜索算法评定圆度误差。该算法对测量点的分布没有要求，测量原理简单，编程容易实现，便于掌握，误差评定精度也较高，为实际圆度误差评定提供一种有效参考。

[1] 机械科学研究所,中国计量科学研究院.GB/T7235-2004产品几何量技术规范(GPS)评定圆度误差的方法半径变化量测量[S].北京:中国标准出版社,2004:3-20.

[2] Endrias D H, Feng H Y. Mininum-zone form tolerance evaluation using rigid-body coordinate transformation[J].Journal of Computing and Information Science in Engineering,2003,3(1):31-38.

[3] 徐志玲,刘宇,程琦.4种圆度误差评定方法分析[J].计量学报,2009,30(Z1):38-41.

[4] 王灿,许本胜,黄美发.区域搜索下圆度误差快速精确评定[J].制造业自动化,2015,37(6):94-96.

[5] 孟凡良,余晓芬,黄开辉,彭鹏.多采样点下圆度误差最小区域评价方法研究[J].机床与液压,2015,43(3):153-157.

[6] Cui Changcai,Che Rensheng, Luo Xiaochuan, et al. From Error Evaluation of Circles Based on a Finely Designed Genetic Algorithm[J].Chinese Journal of Mechanical Engineering,2004,17(1):59-62.

[7] 黄富贵,董兆鹏.圆度误差评定的线性化处理方法[J].华侨大学学报(自然科学版),2011,32(5):492-494.

[8] 李飞,雷贤卿,崔静伟,王海洋.圆度误差的二分法逼近搜索评定[J].北京:河南科技大学学报,2014,35(2):20-23.

Roundness error evaluation based on the algorithm of self-adaptive region searching

GONG Yu-ling1, XU Xiao-dong1, SU Zhao-ning1, GONG Fei2

TH161

：A

1009-0134(2017)03-0056-03

2016-11-28

2014年江苏省大学生创新创业训练计划项目（201412917012Y）；2014年度泰州学院重点教学改革研究课题（14JGA007）

龚玉玲（1978 -），女，湖北人，讲师，硕士研究生，研究方向为精密检测，CAD/CAM/CAE。