小学生自读数学文本能力培养“四部曲”
2017-04-28黄美芳
黄美芳
(顺昌县实验小学,福建顺昌353200)
小学生自读数学文本能力培养“四部曲”
黄美芳
(顺昌县实验小学,福建顺昌353200)
学会学习最基本的能力是学会阅读文本。因此小学数学教师应教给学生阅读文本方法的同时注重学生学习兴趣的培养。让学生在阅读数学文本中能谒见“光彩照人的数学女王”;能倾听到智慧的回响;能唤醒情感的共鸣,从而激起探求的动力。
小学数学;自读;文本数学思想;解题策略;兴趣
何谓“授之以渔”?答曰:学会学习,它是学生的核心素养之一。学会学习最基础的能力就是学会阅读文本。读懂数学文本容易吗?张奠宙教授给出答案:“数学文本呈现的是知识的学术形态,学生比较难懂。有的学生看懂了字面上的意思,甚至题目也会做了,却不知道学这些数学干什么,意义何在,价值在哪儿……”小学阶段如何培养学生自读数学文本的能力?下面谈谈笔者在实践中的做法。培养小学生自读数学文本能力要经历4个阶段。
一、起步篇:读出主要内容
支撑学生数学阅读能力发展的素养是语言知识,这里包括文字语言、符号语言、图形语言。起步阶段重点教会学生对文本符号进行意义的解码,即学会搜集、理解基础信息,从而准确把握学习对象。如左图,五年级上册《精打细算》,笔者让学生带着问题预习:“这节课学什么?”“如何计算?”教学前测结果:知道本节课学习对象是小数除法但对除数是整数感知不强;学生关注计算的结果,对多种计算方法不会进行深入的思考;教材呈现的4种计算方法,他们能读懂前3种方法,第4种方法仅能“看懂字面上的意思”。教学策略:教给多角度比较的方法解读数学文本。首先,对算式进行观察,把新旧知识进行比较,从而准确把握学习对象是“除数是整数的小数除法”;其次,让学生对前2种计算方法进行比较,发现把11.5元换算成115角或11.5元=10元+1.5元再计算,都是用旧知识来解决新问题,在比较中感知解决问题的一般策略;第三,理解竖式意义(符号语言),把1、3两种方法的竖式进行比较,发现除法的竖式都能表示出每次分的过程与分得的结果(商),在情感让学生觉得竖式简单、简洁;最后把3、4两种竖式进行对比,引导思考以下问题:第4种方法商的上面为什么标上数位?这两种方法的竖式中的标注有什么联系?(突出算理,这也是学生理解有困难的地方),最后思考第4种方法还能解决哪些问题呢?使学生脱离具体情境,抽象出计算方法。
在自读数学文本能力培养的起步阶段,学生用比较的方法解读数学文本,人人都可能成为“发现者”,课堂教学因学生的积极参与变得“火热”起来,更多学生体验到被尊重、被肯定的快乐,良好情感体验又促使学生自觉自愿去预习,促成自读数学文本习惯的养成。

二、基础篇:读出隐含的数学思想
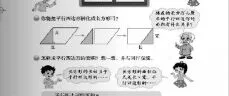
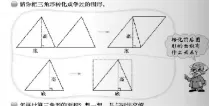
数学课程标准指出:“课程内容不仅包括数学的结论,也应包括数学结论的形成过程和数学思想方法。”当学生能通过比较的方法解读数学文本,第二阶段侧重培养读出数学思想方法的能力。以北师大版五年级上册平行四边行面积的探索活动为例(下图):学生对教材提出的“你能把平行四边行转化成长方形吗?”这个问题的理解停留在事实性水平,他们对为什么要拼成长方形持疑虑,不理解“转化”思想的本质。教学步骤如下:①观察并思考:如何剪、如何拼的、拼成的长方形与原来的平行四边行的面积的联系;②动手剪一剪后思考:不沿着高剪开再拼一拼;新图形与原平行四边行面积的关系?你有办法计算新图形的面积吗?③动口议一议:你认为“转化”是什么的意思?“转化”的目的是什么?有了探索平行四边形面积的经验,在预习三角形、梯形的面积时,学生就能理解图形语言的变化所表达的信息,懂得为什么要这样做,即能读出“转化”思想。在三角形面积探索的教学要注重对转化的第二种思路进行挖掘(如右图),三角形转化成什么图形?转化后的图形与原三角形的面积有什么关系?它和第一种思路有什么共同之处?这些问题促使学生领会“转化”思想的本质,懂得“转化”路径——化未知为已知。
小学阶段的数学思想方法通过解决问题的过程得以体现,学生看到的仅是“只言片语”,课堂教学注重突出数学思想方法的巧妙以及普遍意义,让学生在解题过程中因运用数学思想方法而体验到“柳暗花明”的欣喜,当他们意识到数学思想方法能为问题的解决提供“锦囊妙计”,才能自发、自觉地对文本中的“只言片语”进行推敲,才可能读出隐含的数学思想方法,提高阅读数学文本的深度,同时增长阅读数学文本的能力。
三、发展篇:读出解题策略
几何直观是北师大版教材中运用最多的解题策略,学生对几何直观策略可谓耳熟能详了,那么他们在解题过程中会自觉运用吗?教学现状:大部分学生不会主动的选择画图加强直观,解题时他们反复的询问是否要画图,可见他们把画图当作额外的负担,而不是一种重要的解题策略。因而我们能得出这个结论:大部分学生对问题解决过程采取的方法(策略)视而不见,读出解题策略需要教师有意识的引领,即引导学生思考在解决问题过程中用了什么方法?这种方法有什么好处?可解决哪类问题?下面以列表策略为例加以说明:
如左图:北师大版五年级上册《尝试与猜测》引导学生感悟列表策略我分3个层次:①阅读文本,在新旧方法比较中突出列表策略:“这道题的解法有点意思,以前我们解决问题总会用到算式,今天我们却看到表格。表格也能解决问题?表格又是如何解决问题的?……表格的前两列解决第一个问题,表格的第3列筛选符合第2个条件的结论,从而解决问题;”②练习巩固中建构列表策略:通过由易到难、由具体到抽象的5道练习,引导学生关注问题的特点,思考它与例题是否属于同一类(建模过程)列表法能解决这个问题吗?分成几部分解决?尝试解决。③全课小结中抽象列表策略:列表法适合解决怎样的问题呢?列表策略解决问题步骤有哪些?在期末复习中,一个学生用列表策略解决这道题:被除数、除数都扩大10倍后,商是3余数是9,被除数、除数、商、余数的和是9.6,被除数、除数各是多少?该生把9.6-3-0.9=5.7算出被除数、除数的和后,把问题改编成:被除数、除数的和是5.7,它们的商是3余数是0.9,被除数、除数各是多少?在讲解过程中,他能清楚地表达表格前两列让被除数与除数的和为5.7,第3列中商和余数为3和0.9的就是正确答案(4.5;1.2)。在教师的引领下,学生发现列表策略能为解题提供“脚手架”,使解题过程化繁为简、化抽象为具体,他们品尝到多种的解题策略给他们带来的“甜头”。
当学生能自觉地用不同的方法解决同一个问题,他就真正掌握“渔”法。他们才会从更高的站位去阅读数学文本,而不仅局限于知识与技能的获得。

四、理想篇:读出兴趣
爱因斯坦曾说过:兴趣是最好的老师。当学生能读出学习内容、隐含的数学思想、解决问题的策略,这就可能促成终身学习动力的形成——兴趣。
以下是笔者的教学实例:
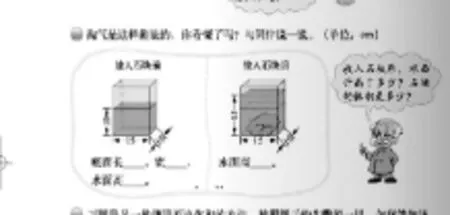
学生能准确描述右图的内容:一个容器装一定量的水,在这杯水里放入不规则石块,水面上升。求不规则石块的体积是多少?教学中笔者故作糊涂地问:“为什么把石头浸入水中?”大部分学生能表达:把不规则物体体积转化为上升部分水的体积……
笔者和学生的对话片断:刚开始认识长正方体,一个学生跑来问笔者有关毫升的问题,解答后笔者随口问:“你从哪儿看来的?”他回答:“学一个新单元,我现在会翻一下整个单元,数学书还是很好看的。”逗他:“和漫画书比谁更好看些?”他很认真的回答:“数学书,有图有知识!”
总之,教给学生阅读文本方法的同时应注重兴趣的培养。让他们在阅读数学文本中能谒见“光彩照人的数学女王”;能倾听到智慧的回响;能唤醒情感的共鸣,从而激起探求的动力。
[1]李伟.关于新课程中重视数学阅读的思考[J].安徽教育学院学报,2005(3).
[2]仲爱云.数学阅读研究概述[J].教学与管理,2009(6).
(责任编辑:陈志华)
