基于蓝牙的自回归匹配室内定位算法

余成波,田林青,王艳丽

(重庆理工大学 远程测试与控制研究所，重庆 400054)



【信息科学与控制工程】

基于蓝牙的自回归匹配室内定位算法

余成波,田林青,王艳丽

(重庆理工大学 远程测试与控制研究所，重庆 400054)

互联网和移动终端的普及推动着LBS向ILBS的发展，而蓝牙与移动终端良好的契合使其成为室内定位技术的首选。介绍了常用的室内定位算法，结合kalman滤波自回归思想提出了一种改进型的非参数化室内定位算法。实验结果表明，改进后的定位算法定位精度在1m以内，能够满足通常应用环境对定位精度的要求，具有广泛的市场价值。

蓝牙；室内定位；自回归

近几年，LBS(基于位置信息服务)技术已经在人们生活中得到广泛应用，比如通过GPS来获得位置信息。然而，随着互联网和移动终端的普及和发展，推动着LBS向ILBS(基于室内位置服务)的过渡。一些景点、商场、博物馆、机场等公共场所需要室内定位提供精确的位置信息。而GPS等室外定位技术由于信号在室内衰减快，不能用作室内定位。室内定位技术主要有蓝牙、ZigBee、wifi、射频识别、超宽带等。由于蓝牙和移动终端的良好契合以及蓝牙4.0版本推出以来的低功耗、低成本、高性价比等优点，使得蓝牙技术成为移动终端室内定位技术[1]的首选。

室内定位算法可以分为参数化和非参数化两种。参数化室内算法是通过计算用户和节点之间的距离建立数学模型进行室内定位，通常有基于到达时间(TOA)、信号到达时间差(TDOA)、信号的到达时间角度(DOA)等方式。但是这种定位方式太依赖数学模型的建立而忽略了环境的复杂度，对于环境引起的多径传播等实际情况未考虑。因此,参数化室内定位算法在实际定位中效果较差。非参数化室内定位算法是把定位环境信息作为待定位目标的坐标函数进行估计，是一种环境感知的定位思想。基于RSSI指纹库的室内定位匹配算法是一种典型的非参数化室内定位算法，分为离线建库和在线匹配两个阶段，其原理是将在线定位阶段的RSSI与离线建库中的RSSI匹配定位。而用得最广泛的匹配算法是k阶近邻算法。

本研究介绍了经典匹配算法(k阶近邻算法)，根据k阶近邻算法存在的缺点结合kalman滤波自回归思想对算法做了改进，提出一种基于蓝牙的自回归匹配室内定位算法。实验结果表明，改进后的算法定位精度高，可广泛用于景点、商场等公共室内定位环境[2]。

1 相关准备工作

1.1 k阶近邻算法

k阶近邻(k-Nearest Neighbour，KNN)算法[3]理论上比较成熟，也是简单的机器学习算法。该方法的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。通俗点说，k阶近邻即是为了从样本空间中找到k个最相似的样本。

在k阶近邻匹配算法中，这个样本空间便是前期所建立的RSSI指纹数据库。通过在线定位阶段的RSSI样本与指纹库中的样本依次进行相似匹配，从中选出k个样本[4]。匹配的思想是利用欧式距离进行筛选。假设实时定位某时刻获得的RSSI信号强度为R=[R1,R2…Rn]，其中n表示蓝牙节点数。数据库中坐标点(x,y)对应的信号强度值为R(x,y)=[R1(x,y),R2(x,y),…,Rn(x,y)]。通过公式

(1)

找到最小的k个L对应的坐标(x,y)，对这k个坐标求质心便得定位坐标。

1.2 卡尔曼滤波原理分析

卡尔曼(kalman)滤波是一种利用线性状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括噪声和干扰，因此也将这种估计过程看作是滤波过程。卡尔曼滤波实际上是通过一种自回归处理算法进行最优估计的过程。其数学思想包括5个核心公式:

x(k|k-1)=A×x(k-1|k-1)+B×u(k)

(2)

p(k|k-1)=A×p(k-1|k-1)×AT+Q

(3)

Kg(k)=p(k|k-1)HT/(H×p(k|k-1)×HT+R)

(4)

x(k|k)=x(k|k-1)+Kg(k)(z(k)-H×x(k|k-1))

(5)

p(k|k)=(1-Kg(k)H)p(k|k-1)

(6)

式(2)、式 (3)是对待测值和最小均方误差的预测，式(4)是kalman增益系数的定义，式(5)、式(6)是对待测值和最小均方误差的最优估计；其中k、k-1代表时刻，u(k)是状态控制量，通常取0；A为状态转移矩阵，H为观测矩阵，通常都取1，AT、HT分别为A、H的转置矩阵；Q，R分别是过程误差和测量误差，分别代表了预测时的方差和测量时的方差；z(k)是k时刻的测量值。x(k-1|k-1)是k-1时刻最优估计值，x(k|k-1)是由k-1时刻对k时刻的预测值，p(k-1|k-1)是k-1时刻最小均方误差，p(k|k-1)是k-1时刻对k时刻的均方误差估计；x(k|k)和p(k|k)是k时刻最优估计值和最优均方误差估计。简化后的公式为：

x(k|k-1)=x(k-1|k-1)

(7)

p(k|k-1)=p(k-1|k-1)+Q

(8)

Kg(k)=p(k|k-1)/(p(k|k-1)+R)

(9)

x(k|k)=x(k|k-1)+Kg(k)(z(k)-x(k|k-1))

(10)

p(k|k)=(1-Kg(k))p(k|k-1)

(11)

整个kalman滤波过程相当于是在预测值x(k|k-1)和测量值z(k)之间权衡，这种权衡不是简单地求平均，而是通过kalman增益Kg进行最优估计。并且最小均方误差p(k|k)的不断更新让整个自回归运算进行下去，从而得到各个时刻的最优估计值。能够看出，一旦初始预测值x(k-1|k-1)、最小初始均方误差p(k-1|k-1)和测量值z(k)确定。影响最优估计结果x(k|k)的就在于Q、R的取值。

2 改进型非参数化室内定位算法

k阶近邻算法是用得最多的RSSI指纹库匹配算法，但是简单地根据欧式距离匹配k(通常取3或者4)个点求质心就决定了算法的定位效果不够好。因为无论是建库阶段还是实时定位所测数据都存在噪声和干扰，而简单通过几个点求质心的方法没能消除噪声和干扰，就会造成定位效果不好或者定位波动过大。基于此，结合卡尔曼滤波的自回归思想，提出一种基于蓝牙的自回归匹配定位算法，消除定位过程中的环境误差和干扰，进行更准确地定位[5]。图1是改进算法的流程图。

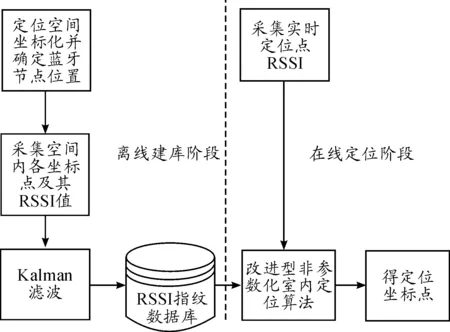
图1 改进型非参数化室内定位算法流程

2.1 离线建库阶段

离线建库的优劣决定了后期在线匹配的精度。在离线建库阶段先对接收信号进行滤波处理，再将处理后的信号存入数据库。

2.1.1 滤波

引入kalman滤波对接收信号强度值进行处理。取第一次扫描到节点n的信号强度值Rn为初始值x(k-1|k-1)；p(k-1|k-1)=0；第二次及以后扫描到节点n的信号强度值作为z(k)；过程误差Q和测量误差R按经验分别取10-6和10-1。随着扫描进行，不断更新最小均方误差p(k|k)让整个滤波过程进行下去，这样采集到的信号强度值便是滤波之后的信号强度。将坐标点(5,4)一次定位采集到的蓝牙节点1的100组经滤波后的信号强度值导入Matlab中仿真，如图2所示。

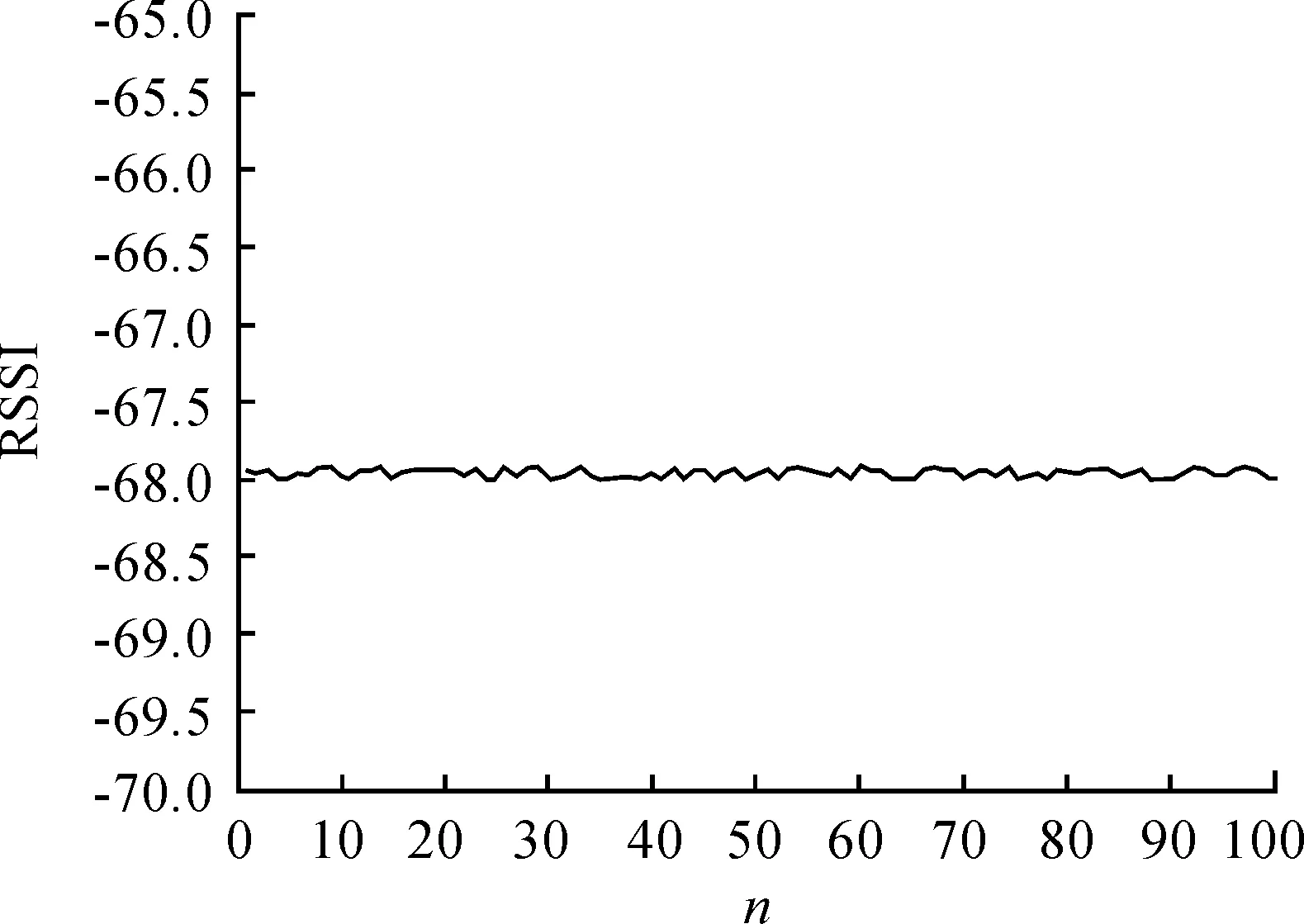
图2 单点一次定位

图2中单点一次定位所接收的信号强度值稳定。这种稳定的效果不难得到，只要Q/R比值足够小，输出结果就会趋近于预测值x(k-1|k-1)。为了验证这种滤波方式对不同坐标点采集信号强度值的差异性，需要对多个坐标进行多次定位来对比。现分别对3个坐标进行10次定位，采集节点1对应的信号强度值导入Matlab，仿真结果如图3所示。

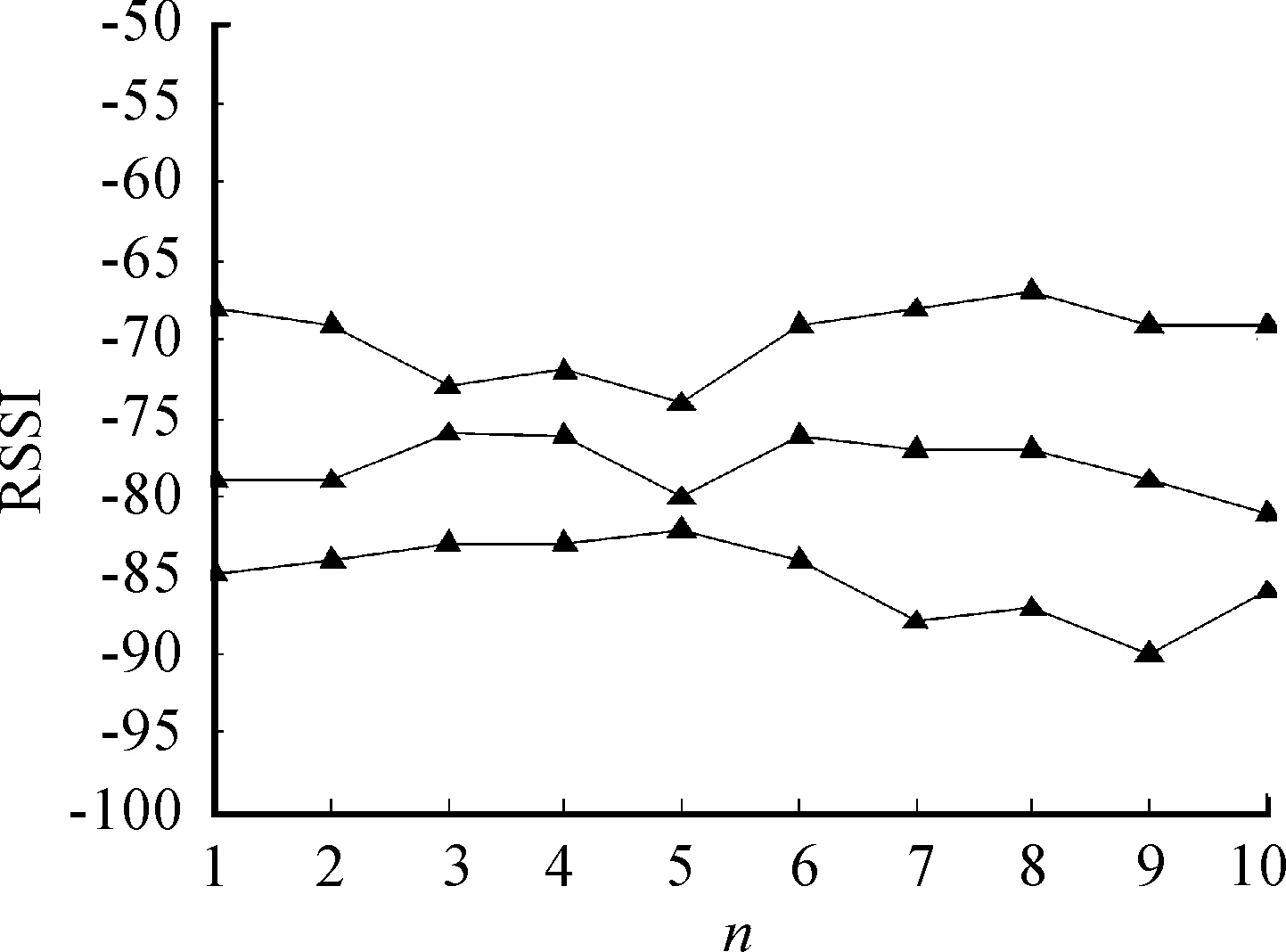
图3 多点多次定位

图3中3条曲线从上到下依次对应坐标(5,4)、(4,5.5)、(6.5,7)。图3中第一条曲线的三角即对应图2中的单点(5,4)一次定位。从图3中可以看出对单点的多次定位采集的信号强度值存在一定的波动，为了尽可能消除这种波动，通过单点不同时间段多次采集求平均的方法更新数据库中的信号强度值即可；并且不同的坐标点之间采集的RSSI存在差异性，这为后期在线定位阶段对不同坐标点进行准确定位提供了可能。

2.1.2 建库

蓝牙节点AP(Access Point)的广播数据主要由唯一标识符UUID、主要值major、次要值minor、信号强度RSSI、设备名称iBeaconName组成[6]。

假如定位空间内有n个蓝牙节点(AP1到APn)，定义坐标为(xi,yi)的定位节点AP(不属于n个蓝牙节点)接收到来自蓝牙节点n的信号强度值为Rn(xi,yi)。将定位节点坐标及其接收到的来自n个节点的信号强度值(滤波之后的)存入数据库中。最终建立指纹数据库如表1所示。

表1 指纹数据库

表1中APn(n=1,2,3,…,n)对应列表示坐标接收到来自节点n的信号强度值。相比于k阶近邻算法的指纹库，加入kalman滤波后建立的指纹库的信号强度值更加准确和稳定。

2.2 在线定位阶段

在线定位阶段是在离线建库阶段完成后进行的。此阶段就是将定位点接收到的蓝牙信号强度值与数据库中进行匹配完成定位。通常采用的匹配算法是1.1中介绍的k阶近邻算法，虽然简单有效，但定位精度不够高。针对定位过程中存在噪声和误差，结合卡尔曼滤波的自回归思想对定位坐标进行最优估计，提出一种自回归匹配室内定位算法。具体思路如下：

1) 利用k阶近邻算法中的欧式距离公式匹配出N个最小的L值。按L值由小到大，其对应的坐标依次为(x1,y1)(x2,y2)…(xn,yn)。

2) 定位坐标(x,y)的横纵坐标x,y应当分开进行最优估计。

3) 令最小均方误差p(k-1|k-1)=0。

4) x(k-1|k-1)=(x1+x2+x3)/3(横坐标的初始估计值)；x(k-1|k-1)=(y1+y2+y3)/3(纵坐标初始估计值)。

5) 测量值z(k)用N个最小L值对应的坐标。z(k)=x1,x2,…,xN(作为横坐标测量值)；z(k)=y1,y2,…,yN(作为纵坐标测量值)。

6) 令Q=10-6，kk=R/Q。

可以看出，自回归匹配定位算法是通过N个点来对定位点横纵坐标分别进行最优估计。通过对方程中某些参数的一些赋值，最后存在两个重要变量，N和kk。N是经欧式距离公式匹配出来的坐标点个数，kk是型定义的比值变量，Q值确定后，kk决定着R值的大小。N和kk不能简单地对其赋值，应该通过实际情况来具体决定。

下面对坐标点(5,4)在不同时间段进行累计20次定位。以N和kk为自变量(由于N值过大会造成定位误差，kk过大会造成仿真时间长并且kk大于103后影响不大，因此给自变量设定范围很有必要)，每次定位结果与坐标点之间的距离s作为因变量[7-8]。当s取得最小值时，求出相应N和kk值

(12)

其中(x0,y0)为实际坐标，(x,y)为定位坐标。当s取得最小时，得到相应的kk和N。

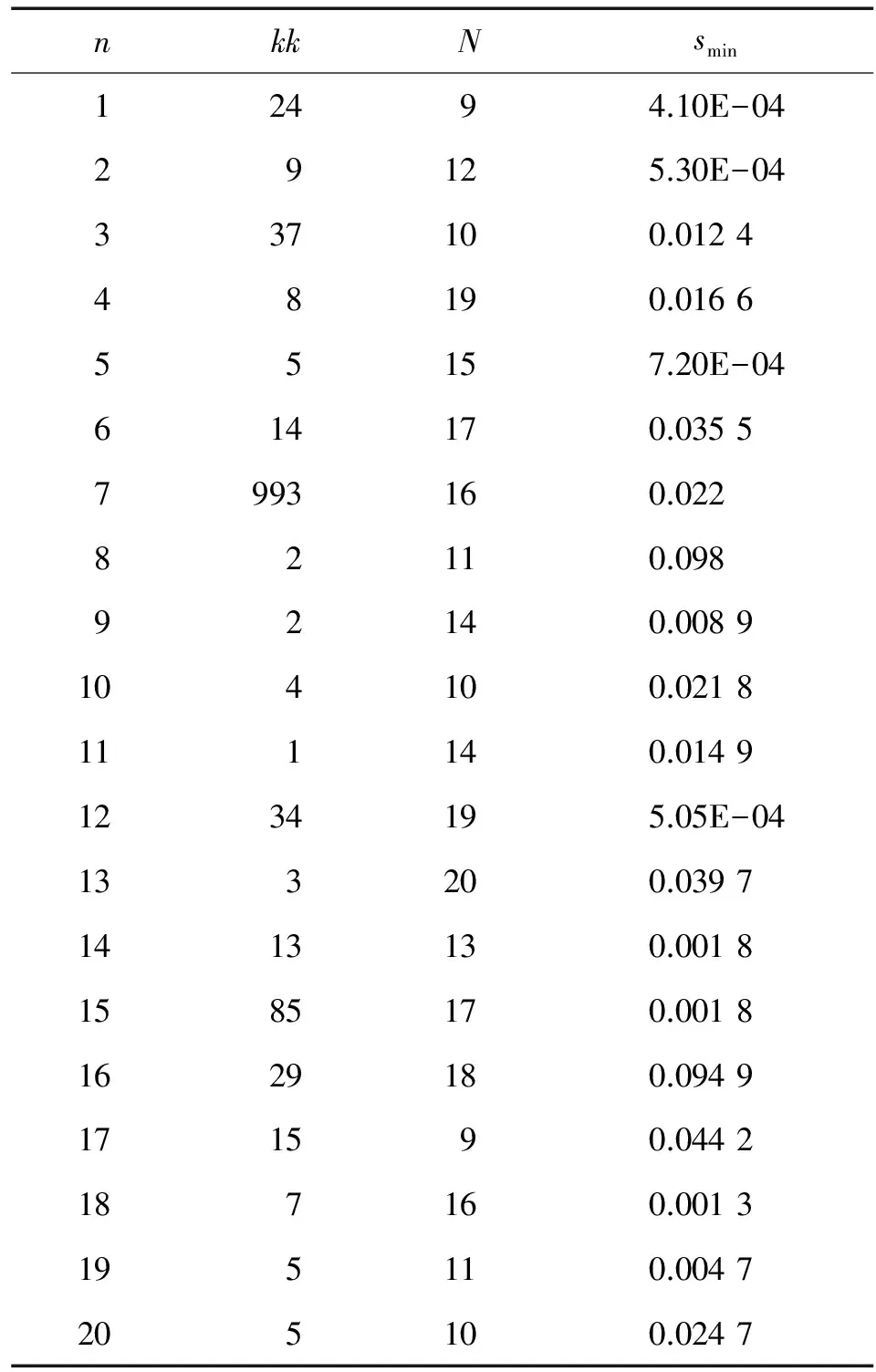
表2 单点多次最优定位

如表2所示。n表示定位次数，kk和N是定位结果和实际位置之间的距离s取最小smin时得到的值[9]。从表2可以看出，N值变化不大，通过求平均得到N=14。但kk是一个跨度较大的变量，不能简单求平均取值，因此

(13)

表示n次定位结果和实际定位点距离之和。当N=14时，S取最小值时便能得到kk值。仿真结果显示当kk=34时，S最小，Smin=26.637 0。

3 实验结果与分析

3.1 实验环境部署

本实验采用Android设备作为离线建库和实时定位阶段的实验设备。蓝牙节点选取ibeacon4.0设备，具体参数如表3所示。

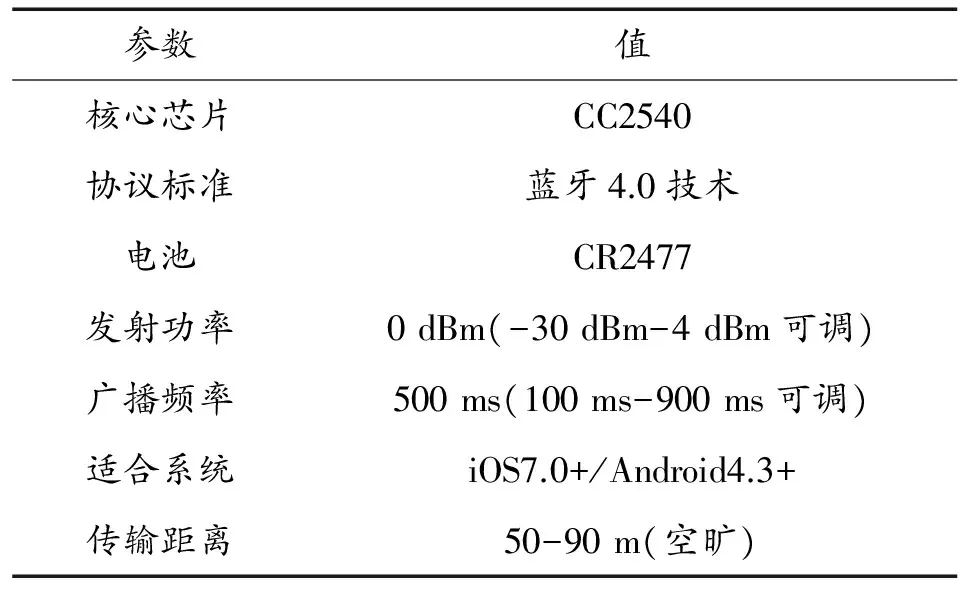
表3 AP参数

在实验区域(10 m×8 m)范围内总共布置6个蓝牙发射节点，逆时针依次为(3,0)、(7,0)、(10,4)、(7,8)、(3,8)、(0,4)6个点。在区域内每0.5m进行采样取点，总共320个采样点。每个采样点分别在不用时间段采集共50组数据求平均存入数据库。蓝牙节点布置如图4所示。

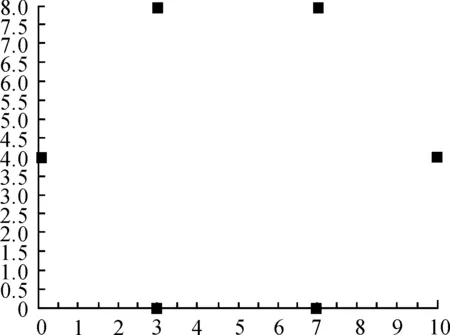
图4 空间格点化及蓝牙节点布置

3.2 实验结果

根据搭好的环境，在实验区域内选取定位点。对定位点进行十次扫描定位，将定位点数据导入Matlab中进行仿真。为了体现改进算法定位的优越性，引入k阶近邻算法进行对比[10]。仿真结果如图5所示。向下的三角形为实际坐标，圆圈为通过k阶近邻算法定位的结果(10次定位存在几个重合点，因此图5中只有8个圆圈点)，星号为改进算法定位点。可以看出k阶近邻算法定位结果误差较大，纵坐标跨度1.5 m左右，横坐标跨度2.5 m左右。而改进后的定位算法横纵坐标跨度大致都在1 m以内，具有较好的精确度。并且将不同坐标点的定位数据导入改进算法进行定位，定位效果明显优于k阶近邻算法，定位误差大致都在1 m以内。

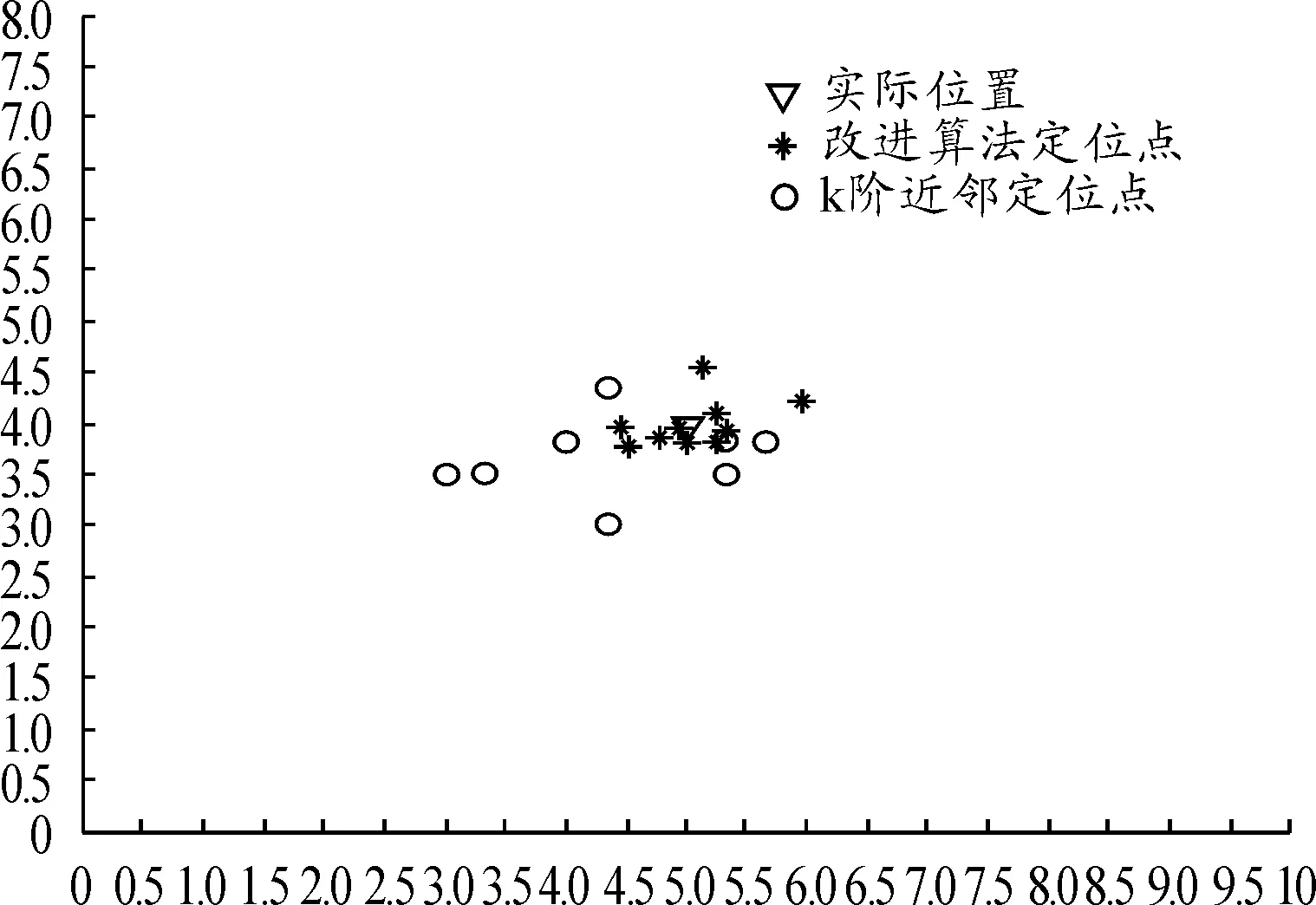
图5 仿真坐标

4 结束语

本文针对当前热门的基于蓝牙4.0的室内定位技术，在室内定位算法上做了改进。实验结果表明，通过引入卡尔曼滤波对接收信号进行处理(尤其是建库阶段)之后再通过自回归匹配算法进行定位的效果明显优于k阶近邻匹配算法，定位精度高、稳定性好，可广泛用于商场、博物馆、旅游景点等室内定位领域，具有很大市场价值。

[1] 赵锐,钟榜,朱祖礼,等.室内定位技术及应用综述[J].电子科技,2014(3):154-157.

[2] 石志京,徐铁峰,刘太君,等.基于iBeacon基站的室内定位技术研究[J].移动通信,2012，39(7):88-91.

[3] 万国峰,钟俊.改进的RSSI测距和定位算法[J].计算机应用研究,2012(11):4156-4158.

[4] MOHAMED ER RIDA.Indoor location position based on Bluetooth Signal Strength[C]//International Conference on Information Science and Control Engineering.[S.l.]:[s.n.],2015.

[5] 江德祥,胡明清,陈益强,等.基于核岭回归的自适应蓝牙定位方法[J].计算机应用研究,2010,27(9):3487-3489.

[6] 莫倩,熊硕.基于蓝牙4.0的接近度分类室内定位算法[J].宇航计测技术,2014(6):66-70.

[7] SANGWOO LEe.Range-free Indoor Positioning System Using Smartphone with Bluetooth Capability [D].Department of Electronics and Computer Engineering,Hanyang University,Seoul,Korea,2014.

[8] 韩旭海,夏文龙,周渊平.基于线性加权的蓝牙室内定位算法[J].计算机系统应用,2015,24(1):119-122.

[9] 陈国平,马耀辉,张百珂.基于指纹技术的蓝牙室内定位系统[J].电子技术应用,2013,39(3):104-107.

[10]ZHANG S,WANG J,LIU X,et al.Range-free selective multilateration for anisotropic wireless sensor networks[C]//in Proc.IEEE SECON.[S.l.]:[s.n.],2012:299-307.

(责任编辑 杨继森)

Recursive Matching Indoor Positioning Algorithm Based on Bluetooth

YU Cheng-Bo，TIAN Lin-Qing，WANG Yan-Li

(Institute of Remote Test and Control, Chongqing University of Technology, Chongqing 400054, China)

The popularity of the Internet and mobile terminal promotes the development of LBS to ILBS. A good combination with mobile terminal makes it the first choice of indoor positioning technology for bluetooth. This paper introduced the common indoor positioning algorithm and proposed an improved non-parametric indoor positioning algorithm combining recursive theory of kalman filtering. The experimental results show that the precision of the improved indoor positioning algorithm is less than 1m, which can meet the requirements of the general application environment for indoor positioning accuracy and has great market value.

bluetooth; indoor positioning; recursive

2016-11-15；

2016-12-15

国家自然科学基金资助项目(61402063)；重庆市科技人才培养计划(新产品研发团队)资助项目(CSJC2013KJRC-TDJS40012)；重庆市高校优秀成果转化资助项目(KJZH14213)

余成波(1965—)，男，博士，教授，主要从事远程测试与控制技术、信号与信息处理研究。

田林青(1991—)，男，硕士研究生，主要从事基于蓝牙低功耗的室内定位技术、无线传感网络研究，E-mail：792085369@qq.com。

10.11809/scbgxb2017.04.021

余成波,田林青,王艳丽.基于蓝牙的自回归匹配室内定位算法[J].兵器装备工程学报，2017(4):95-99.

format:YU Cheng-Bo，TIAN Lin-Qing，WANG Yan-Li.Recursive Matching Indoor Positioning Algorithm Based on Bluetooth[J].Journal of Ordnance Equipment Engineering,2017(4):95-99.

TP98

A

2096-2304(2017)04-0095-05