双向比对技术弹丸空间位置高精度测量方法

张 良，吴海兵，顾国华

(解放军陆军军官学院，合肥 230031)



【装备理论与装备技术】

双向比对技术弹丸空间位置高精度测量方法

张 良，吴海兵，顾国华

(解放军陆军军官学院，合肥 230031)

将弹丸作为未知目标，测距精度受限，且具有较高的系统实现复杂度；将弹丸作为合作目标，提出了一种基于双向比对技术的弹丸空间位置高精度测量方法，给出了相应的系统设计方案；针对此体制的测距及测速理论和仿真分析结果表明：所提方法能够显著提高弹丸空间位置的测量精度，提高系统工作效能。

弹丸位置测量；双向时间比对；合作目标；测距及测速精度分析

在未来的战争中，地面防空武器将面临全天候入侵的各类敌机、空地导弹、巡航导弹、制导炮弹等多种武器的严重威胁，防空系统是否能够有效对空域来袭武器进行拦截，将主要取决于对我方发射拦截弹丸和敌方来袭武器目标空间位置的测量精度以及弹丸起爆位置的控制精度，而精确测量拦截弹丸自身的空间位置则是防空系统有效拦截目标的前提和基础[1]。同时，各国对测速和测距同步技术精度上的要求日趋高标准，使得高精度测速和测距技术成为了众多军事设备改良性能的关键因素[2]。

目前，解决防空弹药对来袭目标精确毁伤的手段主要有两类，一类是使用近炸引信[3]，另一类是利用地面火控雷达实时探测目标的空间位置，在对弹道进行解算后，控制弹丸的发射时机以达到对目标拦截[4]。对于近炸引信，尤其是无线电指令引信目前研究较多，其优点是能大幅提高武器系统对空中目标的毁伤概率，缺点是由于来袭目标运动轨迹、运动姿态和运动速度等的不确定性，使近炸引信容易受干扰，其毁伤效能受到较大限制[5]；对于测控雷达，目标探测距离远、信号处理能力强，但由于雷达系统体积庞大、结构复杂、价格昂贵且探测精度有限，无法大量普及应用[6]。

无线电指令制导体制的优点是弹丸的制导控制部分比较简单，技术上实现比较容易，且价格低廉，缺点是雷达对弹丸和来袭目标的探测精度有限，而且随着制导距离的增大，探测精度也越低，当弹丸在空中飞行的速度达到1 000 m/s以上或者弹丸的雷达截面积(Radar Cross Section,RCS)小于0.4 m2时，很难精确定位[7]。

传统对拦截弹丸定位技术通常基于非合作目标测定的方式，具有较高的解算复杂度且精度受限。本文将弹丸设计为合作目标，提出一种基于双向比对技术的弹丸空间位置高精度测量方法，并给出相应的系统设计方案。即利用现有地面雷达强大的目标探测功能和信号处理能力以及弹丸的通信信道，提高对拦截弹丸的空间定位精度。合作方式用于高速运动目标的定位和测距主要应用在航空卫星测控领域，文献[8]利用星座卫星时间同步和星历更新Kalman滤波器处理星间双向测量数据，能够实现星座卫星时间精密同步和高精度确定卫星轨道，卫星径向轨道滤波收敛后的最大用户测距误差(URE)值小于6 m；文献[9]分析了基于星间测距信息的星座自主导航方法，推导了星间测距信息的位置与时间解耦模型与条件，提出首先进行位置更新，然后进行时间更新的解算流程，最后根据状态方程与量测方程的特点，推导了适合导航星座自主导航解算的分布式卡尔曼滤波算法；文献[10]提出了一种利用改进Kalman滤波融合动力学信息和星间测距信息，并实时修正积分初值的自主定轨算法；文献[11]提出利用少量地面发射源随机工作的方式提供地面基准，将星间测距和地面发射源信息融合进行星座整网定轨，进一步提高定轨精度。

文献[8]到文献[11]的研究重点是如何通过星间测距数据提高定轨精度和实现自主导航，对如何得到高精度的星间距离方面提及较少。本文在文献[12]的基础上，根据弹丸高速运动的特点，应用一种基于双向伪码测距技术，由地面微波雷达和安装于弹丸上的小型应答机协同实现的弹丸空间位置精确测量方法；同时为实现雷达和应答机之间的时间同步，在雷达和应答机的全双工通信终端中引入伪随机码直序扩频同时配置高稳定度频标[13]，并选择双向时间比对方案建立两地时钟的严格同步，最终利用测控通信链路实现雷达和应答机之间的异步传输帧非相干扩频通信[7]，完成双向单程非相干扩频伪距[14]、载波相位测量[15]以及测距测速运算。然后依据弹载双向通信系统的特性，提出了一种基于双向对比算法的弹丸高精度测速及测距方案，并进行了详细的性能分析。实验结果表明所提方案可明显提高弹丸空间位置的测量精度。

1 信号模型

当前目标定位算法主要有到达时间定位法、测向定位法、多普勒频率定位法等。其中，测向定位法、多普勒频率定位法、方位/到达时间定位法的测量精度较低，鉴于弹丸在飞行过程中的运动特性，本文采用适合高速运动体定位的到达时间定位法。双向时间比对法作为到达时间定位法的重要一种，由于双向比对过程中的链路对称，在通信过程中产生的诸多误差因素都在最终的计算中消除，大大的提高了同步和定位精度。下面简要介绍弹载双向比对算法的基本原理。

1.1 弹载双向比对算法测量原理

本文提出的弹丸空间位置测量系统是由地面微波雷达和安装于弹丸上的小型应答机共同完成，通过在地面雷达和弹丸应答机之间建立测控、测距和时间同步链路，实现测控信息的交互，并通过雷达、应答机测距、时间同步等技术保证和提高系统测距及定位的精度。

伪码测距不仅具有测距精度高、捕获时间短、设备简单等优点，而且它避免了多次解距离模糊的复杂运算，保密性和抗干扰性都得到了增强，并且可确保测距的实时性和实时对测距原始观测量进行平滑处理计算，调制载波后可以与其他多种信号同时占用一个射频带宽。故本文采用双向伪码测距技术，利用测控扩频码作为测距码；同时，为实现雷达和应答机之间的时间同步，本文选择双向时间比对方案建立两地时钟的严格同步。具体实现方法：在雷达和应答机的全双工通信终端中引入伪随机码直序扩频并配置高稳定度频标，利用测控通信链路实现雷达和应答机之间的异步传输帧非相干扩频通信，完成双向单程非相干扩频伪距、载波相位测量和测距测速运算。

弹丸经过加装发射和接收设备后，对于地面雷达设备来说可以等同于合作目标。算法通过测量伪码和载波相位等信息，计算得到相对伪距信息，再通过双向比对的方法进行测量并消除时钟差，最终实现高精度测距功能。其工作原理如图1所示。

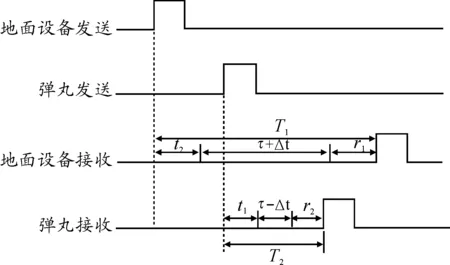
图1 双向比对距离测量原理

地面雷达和弹丸应答机分别以自身时钟为基准发射前向测距信号和后向测距信号，由于双方时间不同步，双方发射的测距信号帧同步之间存在时钟差Δt，雷达通过捕获跟踪双向测距信号可以得到前向测距信号帧同步与反向测距信号帧同步之间的时延T1，该时延包含弹丸与雷达天线间的电磁波传输时延τ外，还包含弹丸发射设备时延t2，雷达的接收设备时延r1以及弹丸与地面设备之间的钟差Δt，其关系为

(1)

同理，通过计算亦可得到时延T2，其关系为

(2)

由以上两式可得地面设备与弹丸之间的相对距离和钟差分别为

(3)

(4)

设t12=t1+r2，t21=t2+r1，则：

(5)

(6)

实际工作中，弹丸与地面设备的测距、时间比对和数据交换过程完全相同，将地面设备的伪距测量结果代入式(4)，将接收到的弹丸传输帧伪码数据代入式(5)，再通过式(6)即可计算出弹丸与地面设备之间的实时距离。

上述处理过程中的T1和T2分别由地面设备和弹丸的码跟踪环路提取，并嵌入到传输帧的数据区中，通过交换链路向对方发送，由于t12和t21可以通过标校获得，从而通过双向比对测距可以得到高精度的距离测量信息。由于距离的一阶微分对应速度，因此求解式的导数即能得出弹丸相对基站的时差变化率，即相对频率准确度。

1.2 信号处理流程

弹载双向通信系统工作时，地面雷达、弹丸应答机分别发射由伪随机码调制的扩频测距信号，在捕获和跟踪到对方发射的信号后提取伪码和载波相位，经过双向比对数据处理后最终得到地面雷达与弹丸之间的距离、速度等信息。图2为弹丸应答机-地面雷达通信与测量信号、信息处理流程图。

信号接收流程：地面雷达接收信号经射频信道变频到中频，再经正交下变频后进行A/D采样处理，采样数据经过数字下变频、扩频、解调出数据信息，然后通过提取帧时标产生帧时标脉冲与本地发射帧时标进行时差测量形成粗测距数据。同时，从解调出的数据中提取出应答机测量伪距值(T2)、弹丸应答机测量伪速值、本地测量伪距值(T1)、本地测量伪速值并按发射时刻配对解算后，最终形成精细测距数据输出。

信号发送流程：接收信号扩频形成的伪码钟与本地发射伪码钟进行相位比较，并经累积平滑处理后得到伪码相位的精测数据，由精测数据和粗测数据合成伪距数据值T1。伪距数值T1经滤波、缓存，在下一发射时刻打包格式化到器间测控发射数据帧中，再经过扩频、调制最终由射频BPSK调制发射信道发射出去。

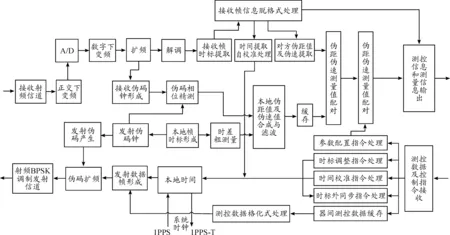
图2 弹载双向通信系统信号处理流程

整个信号处理流程中，本地时间是发射信号的基准时刻，以一定的系统时钟工作，可以产生内部发射时标，并生成相干的1 PPS-T输出信号作为系统测试信号。系统在时标外同步指令的驱动下，可实现本地时间与外部输入的1 PPS信号的同步；本地的时间单元在时标调整指令、时间校准指令的控制下，也可实现本地时间的校准。

2 系统性能分析

2.1 测速精度分析

在地面雷达与弹丸应答机之间采取非相干扩频测距测速的情况下，雷达载波跟踪环在两个时刻的载波相位差对应单程载波多普勒积分。因此，通过测量两个时刻的载波相位差便能够得到弹丸的速度，所以有

(7)

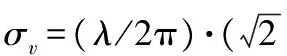
PLL热噪声为

应用专用计算软件对发电电动机进行背靠背起动仿真计算，发电机和电动机励磁电流分别给定1.0(p.u.)，励磁控制方式为恒励磁电流调节方式。所分析的起动过程为压水起动，计算中考虑了各种损耗对电机产生的阻力矩，包括发电机的上导轴承、下导轴承、水导轴承及推力轴承的损耗等等[7]。另外，起动过程中水轮机的输入转矩给定22%Tn。电机的加速时间为104 s左右，即机组从静止状态加速到额定转速的时间(不包括同步并网的时间)见图5。

(8)

热噪声引起的载波环跟踪误差与环路带宽、环路载噪比的两维关系曲线如图3所示。

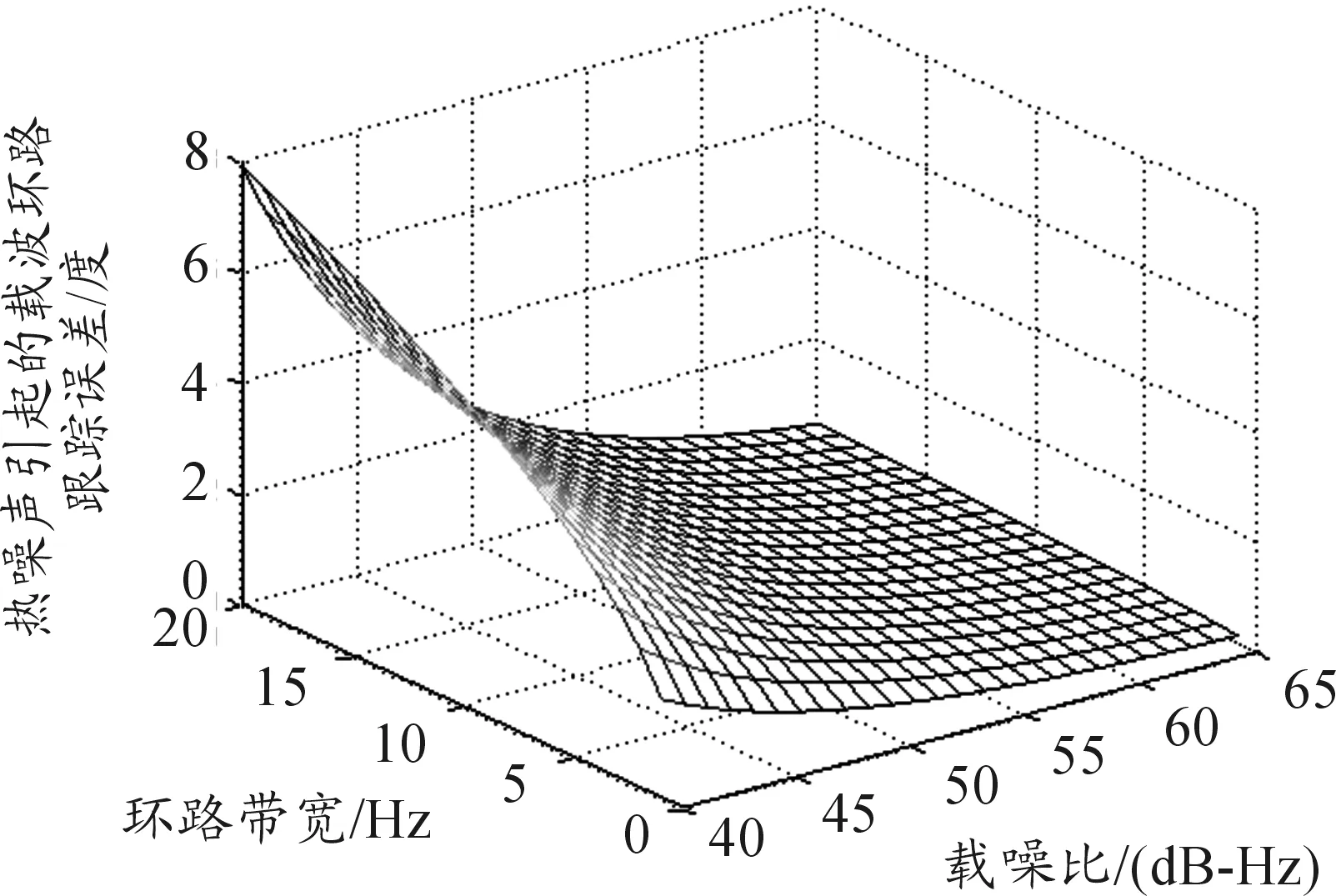
图3 载波环跟踪误差与载噪比、环路带宽的关系

其中当载噪比固定为50 dB-Hz时，与环路带宽的一维关系曲线如图4所示。

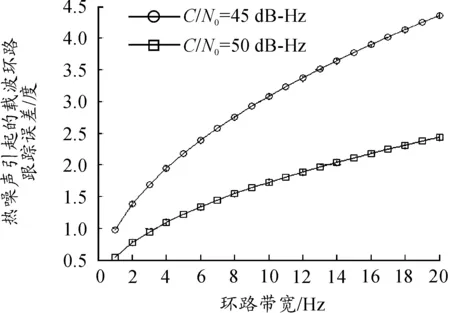
图4 载波环跟踪误差与环路带宽的关系

当环路带宽固定为10 Hz、18 Hz时，与环路载噪比的一维关系曲线如图5所示。

阿仑方差振荡器相位噪声(方案设计中选择三阶环)为

(9)

动态应力误差(三阶环)为

(10)

图5 载波环跟踪误差与载噪比的关系

所以PLL跟踪误差为

(11)

由式可以看出，载波跟踪动态应力误差与环路阶数、环路带宽和加速度动态有关，由于地面雷达—弹丸应答机相对距离变化率范围在正负60 m/s范围内，加加速度动态应该不大，而且也只是瞬时的，因此载波环跟踪动态应力误差引起的测速误差可以忽略不计。指标估算时环路带宽Bn选择18 Hz(该带宽可以满足测量通信设备动态要求)，阿仑方差σA(τ)为1×10-12(假设值)，测速时间间隔Ts选取为100 ms(方案暂定)，因此总测速误差为

(12)

2.2 测距精度分析

采用伪码测距体制，测距误差主要来源于码环对接收扩频信号的跟踪误差、传输路径(含接收通道)附加时延不确定度、相对距离变化与时差引起的误差以及由晶振频率稳定度带来的测距误差。

2.2.1 码环(即DLL)跟踪误差

码环跟踪误差主要由3部分组成：热噪声引起的距离跟踪颤动、由于跟踪环路跟踪目标动态引起的动态应力误差和多径误差。通常情况下，码环存在动态跟踪误差，但由于码多普勒频率和载波多普勒频率是成固定比关系的，采用载波环辅助码环技术可以消除码环大部分的动态误差，因而码环的动态跟踪误差很小，可以忽略不计。

非相干码跟踪环热噪声颤动误差(1σ)为

(13)

对于超前滞后相关器，有F1=1/2，F2=1，相关间隔选为1/2 chip，即d=1/2，码速率为10.23 MHz，故式可表示为

(14)

其中，C/N0为载噪比，Bn为环路带宽，T为预检测积分时间。系统方案设计中选择T=1 ms。由于码跟踪环由载波环辅助，因此只需很小的环路带宽就可以完成对伪码的精确跟踪。热噪声引起的码环跟踪误差与环路带宽、环路载噪比的两维关系曲线如图6、图7所示。

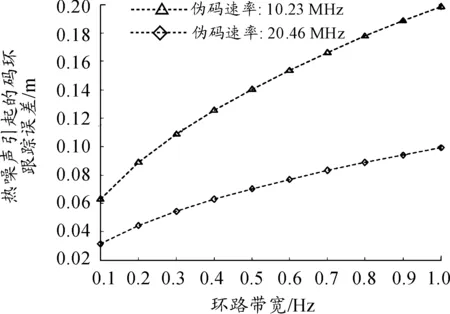
图6 热噪声引起的码环跟踪误差与环路带宽的关系

图7 热噪声引起的码环跟踪误差与载噪比的关系

其中当载噪比固定为50dB-Hz时，与环路带宽、环路载噪比的两维关系曲线如图8所示。

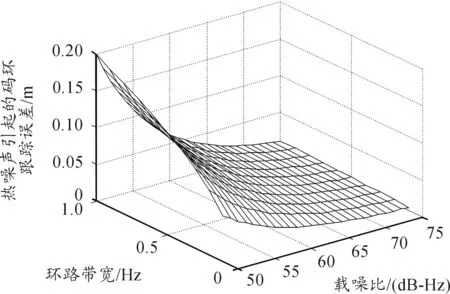
图8 码环跟踪误差与与载噪比、环路带宽的关系

当环路带宽固定为0.1Hz时，与环路载噪比的一维关系曲线如图9所示。

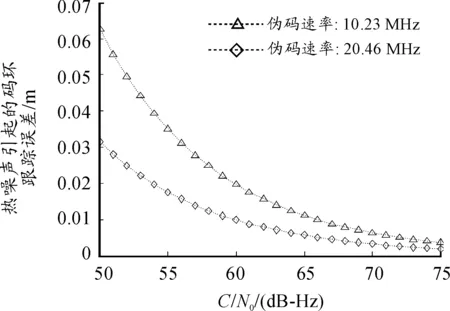
图9 热噪声引起的码环跟踪误差与载噪比的关系

容易看出：当环路带宽选为0.1Hz，伪码速率为10.23MHz时，由热噪声引起的测距误差(3σ)小于0.062 7m。多径误差与多路径信号与直达路径信号的相对强度、相对延迟有关，而多路径信号与直达路径信号的相对强度、相对延迟与接收天线和其所处的环境、使用条件有关，需根据具体情形综合分析。

2.2.2 传输路径(含接收通道)附加时延不确定度

传输路径主要包含天线、收发通道，附加时延不确定度包含绝对时延不确定度和时延变化不确定度。天线和收发通道的绝对时延标定不确定度，随着入射角、温度和信号强度的时延变化不确定度，均会等效为测距误差。

天线和收发通道的绝对时延不确定度(即微波雷达系统距离差或称微波雷达测距系统标校值)可通过校准通道实时标校得到，即利用通道时延自校环路，可以估计得到通道时延，与正常接收通道间的伪距测量值进行相减从而消除零值的漂移。

2.2.3 相对距离变化与钟差引起的误差

地面雷达和弹丸应答机有各自不同的时钟基准，因此必然带来它们之间时钟同步问题，即存在钟差，影响测距精度。在钟差Δt期间地面雷达—弹丸应答机存在相对运动，即相对距离变化将带来相对距离测量的偏差。经计算，当相对径向运动速度为60m/s时，钟差Δt为0.1ms，即可保证由此引入的测距误差小于0.006m。

2.2.4 晶振频率稳定度对测距的影响

由于测距频标的输出频率并不是标称频率，但系统仍然按照标称频率计算距离，由此引起一定的距离测量误差。距离越大，误差越大，对于本方案中系统参数，频标稳定度引起的测距误差估算如下，对于100km作用距离，测量误差约为

(15)

这对于10m左右的测距精度指标而言，是可以忽略不计的。

根据以上分析，测距总误差可表示为

(16)

(17)

(18)

其中：Δρ为测距误差；Δρ0为测距系统误差，经标校后剩余误差可以认为0.03 m；Δρn为环路跟踪误差，即3σtDLL，为码跟踪环热噪声引起的3σ随机测距误差；Bn=0.1 Hz，码环噪声带宽；C/N0，载噪比，用dB-Hz表示；c=2.997 924 58×108m/s为真空中光速；λcc=2.997 924 58×108/10.23×106=29.305 2 m/chip；T=1 ms，为预检测积分时间。

图10给出了1.5 m～100 km时，本文方法测距精度仿真值与系统指标的对比曲线。根据链路计算结果可知，在各工作距离段均能满足指标要求。在实际设备工作中，存在系统零值标定误差和零值漂移影响等因素，近距离下通过零值校准，测距精度可以控制在0.1 m之内，远距离下不经零值校准测距精度仍可以控制在1 m之内。这一指标远高于目前传统弹丸位置测量精度。

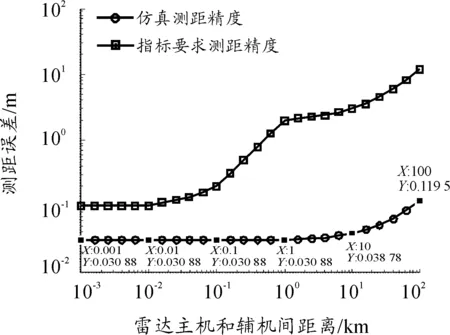
图10 本文方法的测距误差仿真值与指标要求对比

3 结论

本文提出了一种基于双向对比算法的弹丸高精度测距及测速方法，并给出了相应的测距及测速方案。理论计算和仿真分析结果表明了所提方法的可行性。在最低载噪比47dBHz，环路带宽为18Hz情形下，测速误差优于2e-3m/s，测距精度优于1m。将所提方法应用到高速弹丸的位置测量，可以较好地解决传统基于非合作测量方式的不利影响，明显提高系统性能。

[1]TINDELLK,HANSSONH,WELLINGSAJ.Analysingreal-timecommunications:controllerareanetwork(CAN)[C]//IEEEReal-TimeSystemsSymposium,1994:259-263.

[2]LIXR,JILKOVVP.Surveyofmaneuveringtargettracking.PartI.Dynamicmodels[J].IEEETransactionsonaerospaceandelectronicsystems,2003,39(4):1333-1364.

[3]GIRODL,ESTRIND.Robustrangeestimationusingacousticandmultimodalsensing[C]//IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems,2001:1312-1320.

[4] 谭述森.导航卫星双向伪距时间同步[J].中国工程科学,2006,12(8):70-74.

[5]SIMONEL,GELFIISAD,COCCHIS,etal.Noveldigitalplatformfordeepspacetransponders:thetransmitterside[C]//2004IEEEAerospaceConference,2004.

[6] 黄波,星间测距与导航卫星自主定轨研究[D].武汉：华中科技大学,2011.

[7] 李俊生,伪码测距算法研究与仿真[D].长沙：国防科学技术大学,2006.

[8] 龚晓春,分布式微型航天器的时钟同步研究[D].哈尔滨：哈尔滨工业大学,2007.

[9] 李梦,载波相位平滑伪距在双向测距与时间同步中的应用[C]//第四届中国卫星导航学术年会论文集-S4 原子钟技术与时频系统,2013.

[10]彭军,无线通信系统定位算法研究及误差分析[D].成都：电子科技大学,2008.

[11]张伦,星地时间同步技术的研究[D].西安:西安电子科技大学,2008.

[12]翟政安,航天器的非相干高精度测速方法及实现[J].电讯技术,2005,45(2):86-89.

[13]马宏,王元钦,陈谷仓,编队小卫星间相对测距和时间同步方法研究[J].装备指挥技术学院学报,2006,17(2):67-71.

[14]MITRASK,KUOY.Digitalsignalprocessing:acomputer-basedapproach[M].NewYork:McGraw-Hill,2006.

[15]OPPENHEIMAV,WILLSKYAS,NAWABSH.Signalsandsystems[M].NJ:Prentice-HallEnglewoodCliffs,1983.

(责任编辑 周江川)

Novel Method for Exact Position Calculation of ProjectileUsing Bidirectional Time Alignment Technology

ZHANG Liang, WU Hai-bing, GU Guo-hua

(Army Officer Academy of PLA, Hefei 230031, China)

In this paper, a high precision method for projectile position measurement based on bidirectional time alignment technique was proposed firstly. Then the corresponding system implementation scheme was designed. Both theoretical and simulated results show that the proposed method can improve measurement precision and working efficiency of the system.

projectile position measurement; bidirectional time alignment; cooperative target; accuracy analysis of distance and velocity measurement.

2016-11-27；

2016-12-25

国防装备预研共用技术

基金项目(9140A05020114JB91064)

张良(1984—)，男，博士，讲师，主要从事兵器科学与技术研究。

10.11809/scbgxb2017.04.002

张良，吴海兵，顾国华.双向比对技术弹丸空间位置高精度测量方法[J].兵器装备工程学报，2017(4):8-13.

format:ZHANG Liang, WU Hai-bing, GU Guo-hua.Novel Method for Exact Position Calculation of Projectile Using Bidirectional Time Alignment Technology[J].Journal of Ordnance Equipment Engineering,2017(4):8-13.

TN957；TJ01

A

2096-2304(2017)04-0008-06