弹丸侵彻运动钢板的数值模拟

张学伦，刘宗伟，张团，王昭明

(重庆红宇精密工业有限责任公司，重庆 402760)



【装备理论与装备技术】

弹丸侵彻运动钢板的数值模拟

张学伦，刘宗伟，张团，王昭明

(重庆红宇精密工业有限责任公司，重庆 402760)

针对反舰弹丸打击运动目标，运用ANSYS/LS-DYNA有限元软件对反舰弹丸侵彻不同组合模式、运动状态钢板的过程进行了数值模拟，分析了钢板的单层厚度、总厚度、运动状态对反舰弹丸侵彻过程的速度、姿态及受力状态的影响特性。数值模拟结果表明，钢板的总厚度是影响弹丸速度变化的主要因素，单层钢板的厚度是影响弹丸姿态和壳体应力状态的主要因素，钢板运动对弹丸速度变化和壳体应力状态的影响相对较小，但对弹丸的姿态影响较大。

反舰弹丸；钢板；侵彻效应；数值模拟

近年来发生的战例表明，能否快速有效地摧毁敌方大中型水面舰艇是取得现代高技术局部战争胜利的关键之一。反舰弹丸作为水面舰艇的克星，提高其对目标的毁伤威力已成为了该技术领域的重要研究热点。弹丸对舰艇甲板或侧舷的侵彻过程是一个十分复杂的冲击动力学问题，对反舰弹丸侵彻静态钢板的理想状态作用过程，国内外诸多学者进行了大量的理论分析、数值模拟和试验研究。然而，实战中目标通常处于运动状态，弹丸与舰船目标的作用过程为并非静止的理想状态[1-2]。少数学者对弹丸侵彻移动靶板进行了研究[3-10]，但未充分考虑靶板的运动方向及靶板组合模式对侵彻效应的影响。本文利用动力学分析软件LS-DYNA对弹丸侵彻不同组合模式、运动状态钢板的过程进行了数值模拟分析，试图获得钢板厚度、运动参数对反舰弹丸侵彻过程的影响特性，为反舰弹丸高效毁伤运动目标提供参考。

1 模型建立

大量试验结果表明，LS-DYNA非线性有限元软件是分析弹丸侵彻钢靶问题的有效手段[11]。

1.1 几何模型

为了较好地描述弹丸与目标靶板的复杂交汇状态，对弹丸与靶板交汇的初始状态建立了如图1所示的几何模型。X轴平行于弹丸初始状态轴线，Y轴和Z轴垂直于弹丸轴线，Vd为弹丸着靶速度，Vbx、Vby、Vbz分布为钢靶板沿其坐标系X轴、Y轴、Z轴方向的运动速度，α角为弹丸着角，γ角为侵彻过程中弹丸轴线与水平方向之间的夹角，表征弹丸侵彻过程中姿态的变化情况，规定γ角逆时针为负，顺时针为正。在数值模拟中，弹丸采用CRH=3的卵形头部弹丸，弹体长径比为5，弹丸外形为φ260 mm×1 300 mm，弹重300 kg；靶板为2 500 mm×2 500 mm的方形靶板。

1.2 有限元计算模型

在ANSYS/LS-DYNA有限元软件中，弹丸和钢靶板按三维实体Solid164八节点六面体单位进行划分，采用Lagrange方法进行计算。弹体与靶板之间的接触界面采用面-面接触的侵蚀算法。

1.3 弹、靶材料模型

弹丸和靶板均采用Johnson-Cook模型，对各向同性材料，该模型可以准确描述金属材料行为，能较好地描述金属材料的加工硬化效应，应变率效应和绝热升温引起的软化效应，适用于金属由准静态到大应变、高应变率和高温情况下的计算。Johnson-Cook模型[10]应力应变关系见式(1)：

(1)

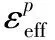
1.4 边界条件

弹丸与靶板的初始速度方向分别如图1所示，弹丸的速度Vd为750 m/s；靶板的速度Vb分别为0 m/s、±18 m/s(舰船的常规速度30节)；着角α为45°。

表1 弹体材料模型参数

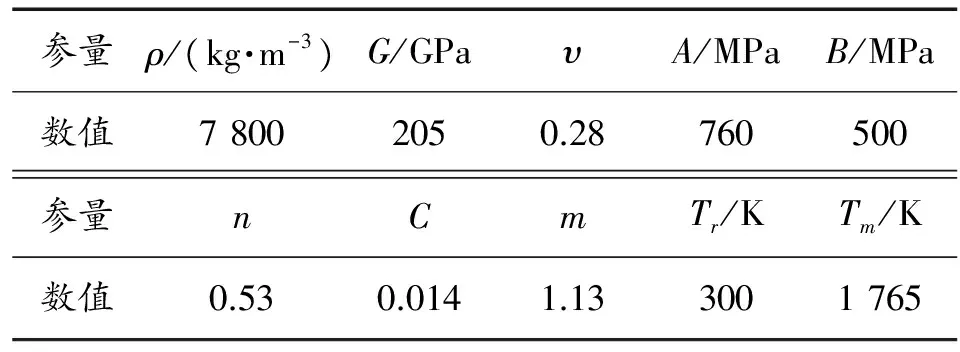
表2 靶板材料模型参数

2 计算结果及分析

利用上述模型，分别对反舰弹丸侵彻不同组合模式、运动状态钢靶板的过程进行了数值模拟分析，具体工况条件列于表3。表3中靶板运动坐标系与图1所示一致，即弹道方向为X向，弹道的上下方向为Y向(向上方向为正向)，弹道的左右方向为Z向(正负向遵守右手定则)。

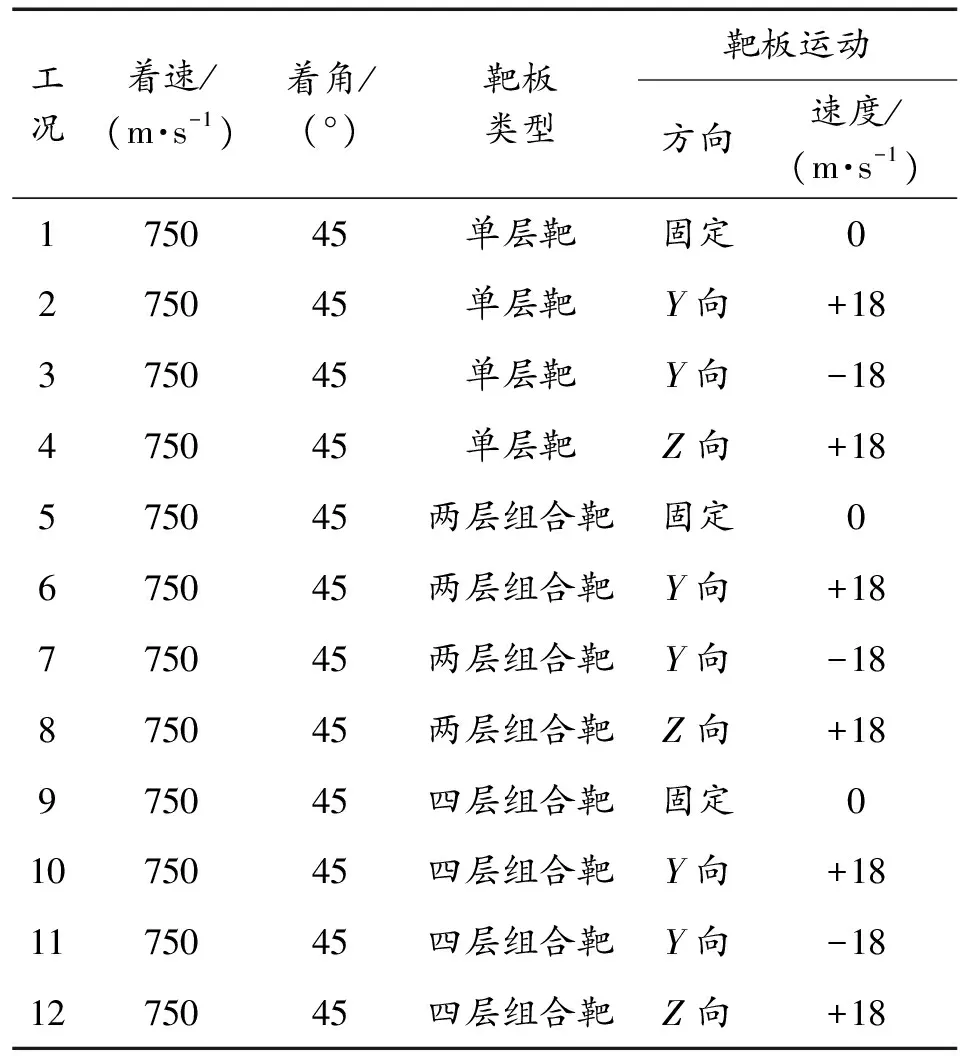
表3 计算工况

工况1～工况4中，钢靶板的组合模式为单层靶(厚度32mm，倾斜角度45°)；工况5～工况8中，钢靶板的组合模式为两层组合靶(厚度60mm+20mm，垂直间距2m，倾斜角度45°)；工况9～工况12中，钢靶板的组合模式为四层组合靶(厚度32mm+18mm+10mm+10mm，相邻层垂直间距2m，总垂直间距6m，倾斜角度45°)。

2.1 靶板组合模式的影响

反舰弹丸侵彻不同组合模式静止钢靶板的速度变化曲线如图2所示。工况1、工况5、工况9的剩余速度分别为736.2m/s、706.9m/s、717.9m/s。从图2可以看出，工况5靶板累计厚度最大，工况5弹丸的剩余速度最小，因此，在靶板组合模式中，靶板的累计厚度是影响弹丸剩余速度的最主要原因。

图2 工况1、5、9弹丸速度变化曲线

弹丸侵彻不同组合模式静止钢靶板的姿态变化情况如图3所示。在工况1中，弹丸出单层靶时的γ角为0.4°；在工况5中，弹丸出第二层靶时的γ角为-1.85°；在工况9中，弹丸出第四层靶时的γ角为-3.1°。从图3可以看出，工况1和工况9的γ角变化基本一致，这表明工况9中第二层至第四层靶板对γ角影响较小；工况5中，在侵彻第一层靶板后γ角为2.39°，出第四层靶时γ角分别为-3.1°，侵靶过程弹丸姿态变化相对较大。因此，当单层靶板相对较薄时，对弹丸姿态影响较小；当单层的靶板相对较厚时，对弹丸姿态影响较大。

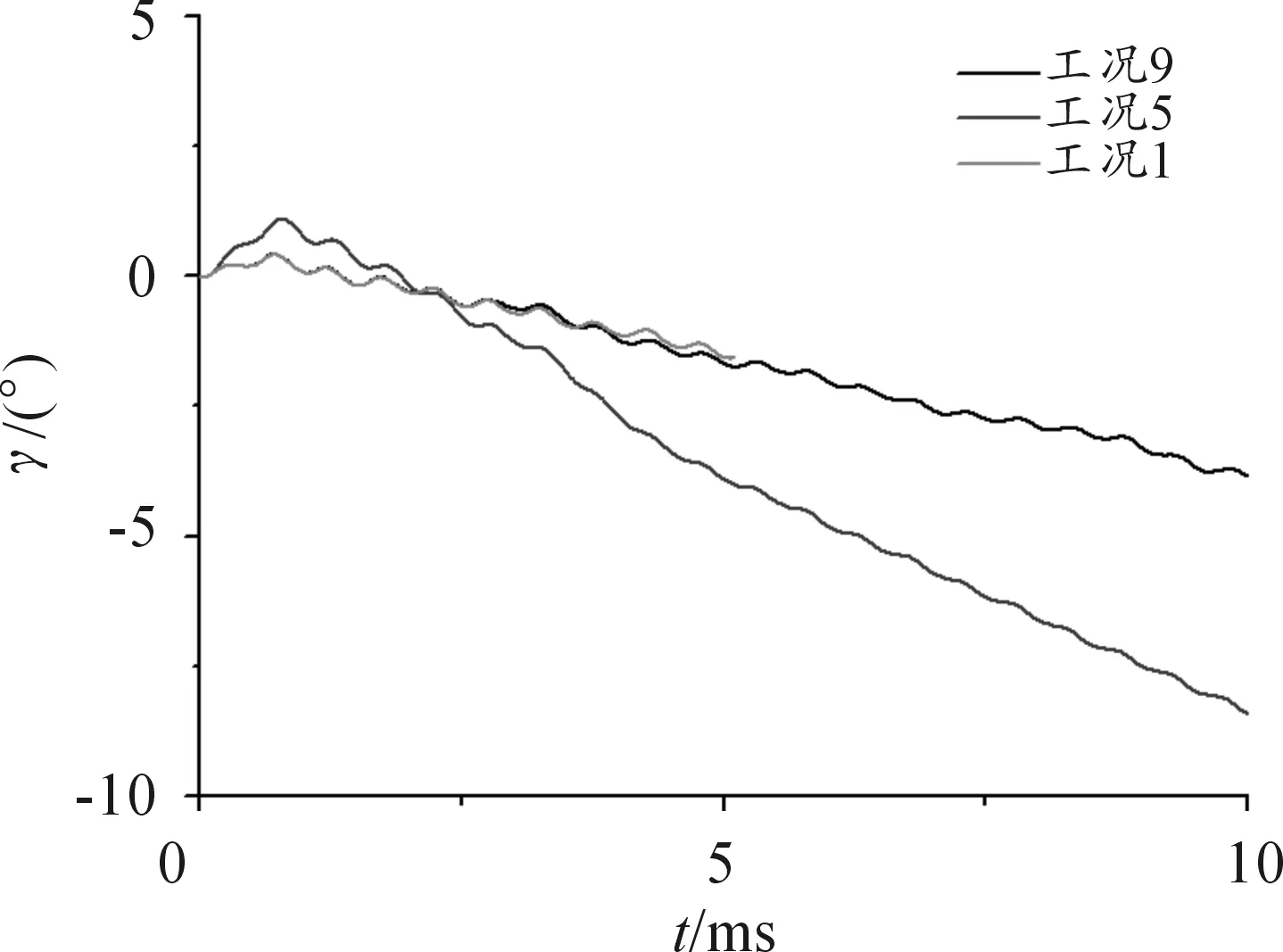
图3 工况1、5、9弹丸姿态变化曲线

弹丸侵彻不同组合模式静止钢靶板的壳体典型单元应力状态如图4所示。工况1、工况5、工况9弹丸壳体典型单元应力峰值分别为1 716 MPa、2 061 MPa、1 713 MPa。从图4可以看出，在3种工况中，工况5壳体应力峰值最大，工况1和工况9壳体应力峰值基本相同，这说明每层靶板的厚度是影响壳体应力的主要因素。

图4 工况1、5、9壳体单元应力变化曲线

2.2 靶板运动的影响

1) 靶板运动对弹丸速度的影响

弹丸侵彻单层钢靶的速度变化曲线如图5所示，在工况1～工况4中，弹丸的剩余速度范围为735.8～737 m/s；弹丸侵彻两层组合钢靶的速度变化曲线如图5所示，在工况5～工况8中，弹丸的剩余速度范围为705.9～707.9 m/s；弹丸侵彻四层组合钢靶的速度变化曲线如图6所示，在工况9～工况12中，弹丸剩余速度范围为717.1～718.9 m/s。从图5～图7可以看出，在其他条件相同的情况下，靶板运动对弹丸剩余速度的影响不超过0.3%，因此可认为靶板的运动对弹丸速度的影响较小。

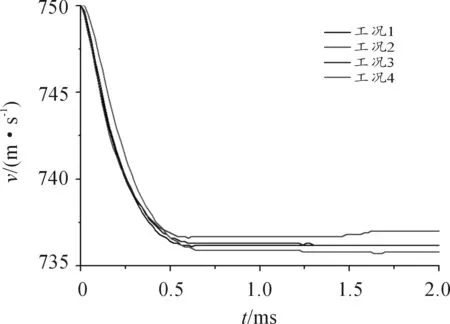
图5 工况1～工况4弹丸速度变化曲线

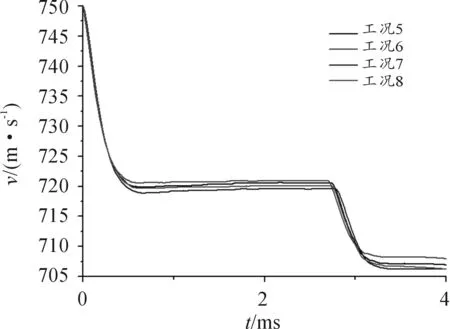
图6 工况5～工况8弹丸速度变化曲线

2) 靶板运动对弹丸姿态的影响

反舰弹丸侵彻单层靶、两层组合靶和四层组合靶的γ角变化曲线分别如图8、图9和图10所示。从图8～图10可以看出，在其他工况条件相同的情况下，靶板运动方向对弹丸出靶姿态，尤其是靶后运动姿态变化趋势有较大影响。

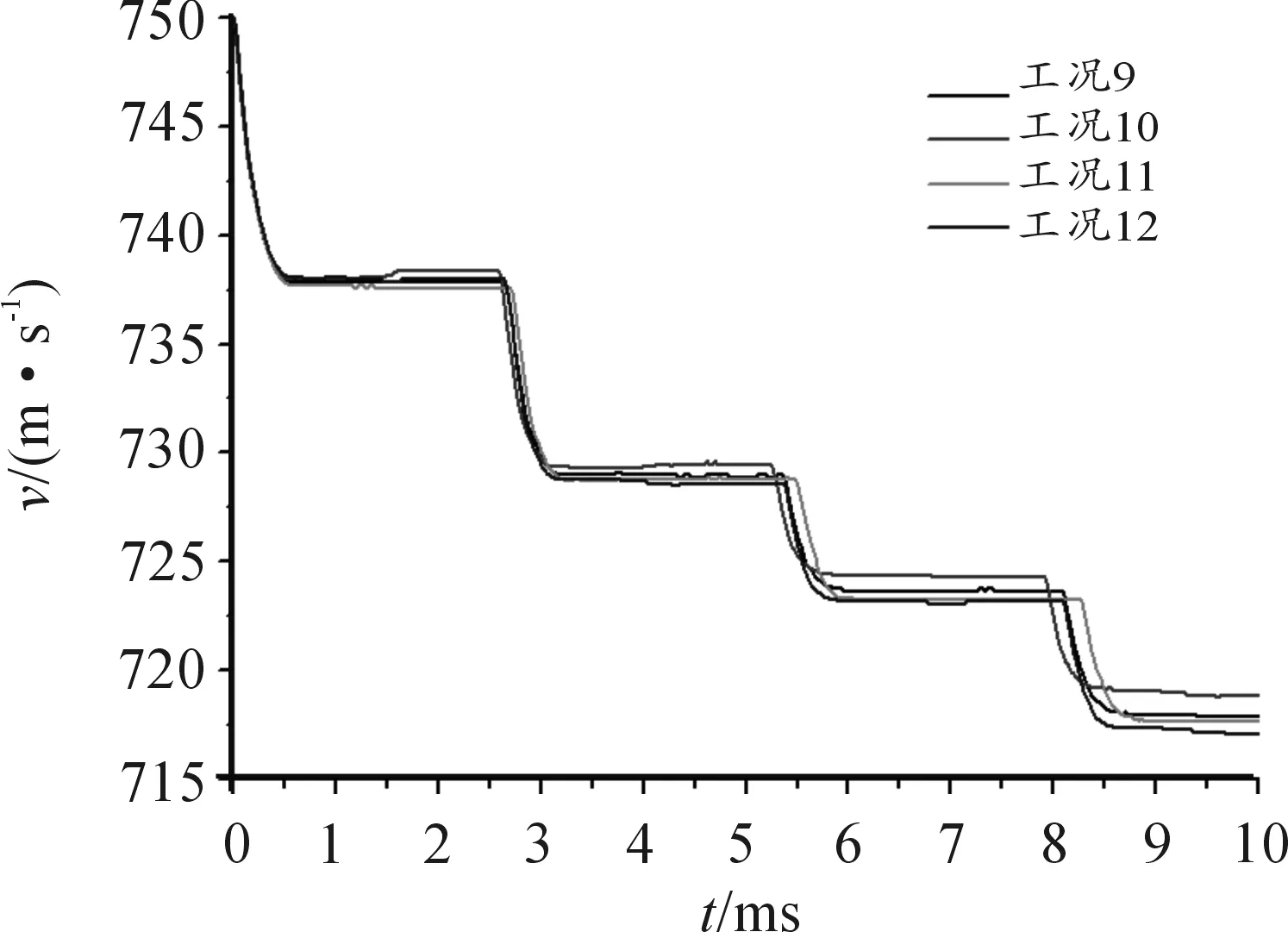
图7 工况9～工况12弹丸速度变化曲线

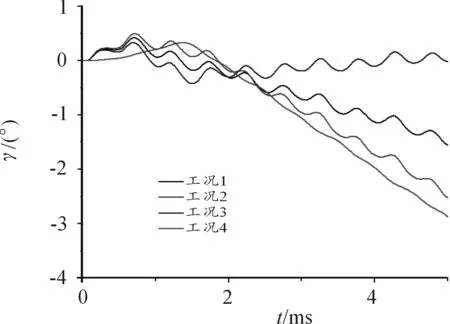
图8 工况1～工况4弹丸姿态变化曲线

图9 工况5～工况8弹丸姿态变化曲线

图10 工况9～工况12弹丸姿态变化曲线

3) 靶板运动对壳体应力的影响

弹丸侵彻单层、两层组合靶和四层组合钢靶的壳体典型单元应力变化曲线分别如图11～图13所示。从图11～图13可以看出，在其他条件相同的情况下，侵彻单层靶、四层组合靶壳体典型单元应力峰值为1 590～1 778 MPa,侵彻两层组合靶壳体典型单元应力峰值为2 027～2 061 MPa,壳体典型单元应力峰值最大相差11.8%。因此，靶板的运动对壳体应力具有一定的影响。

从图13还可以看出，工况9～工况12中侵彻第二、三、四层靶板时，壳体应力峰值逐渐增大，这是由于弹丸着靶姿态变差导致的。因此，弹丸的着靶姿态也是影响壳体应力峰值主要因素之一。

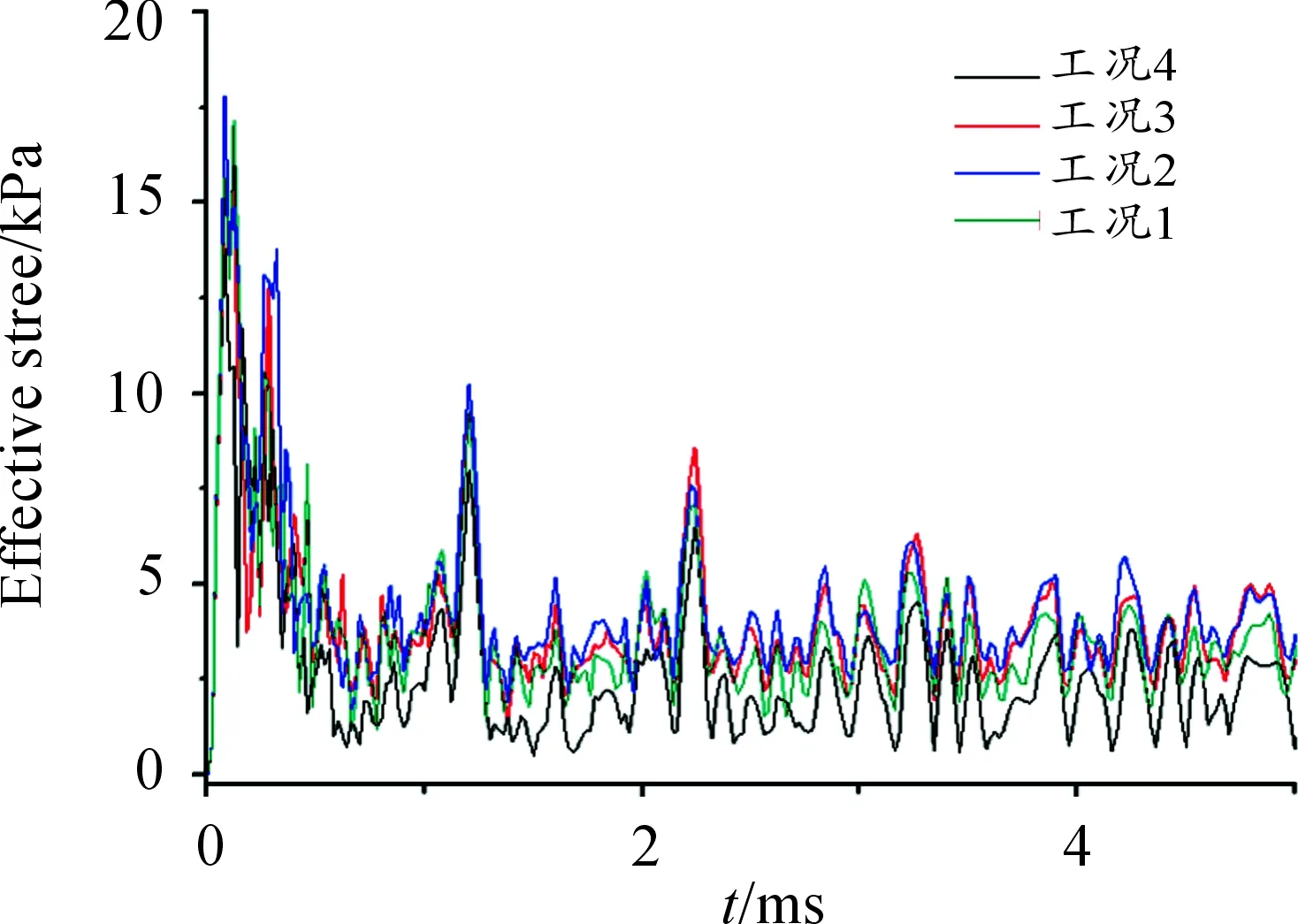
图11 工况1～工况4壳体单元应力变化曲线

图12 工况5～工况8壳体单元应力变化曲线

图13 工况9～工况12壳体单元应力变化曲线

3 结论

1) 钢靶板的组合模式对弹丸的侵彻过程有重要影响：单层靶板相对较薄时，对弹丸姿态影响较小，单层靶板相对较厚时，对弹丸姿态影响较大；单层靶板的厚度是影响壳体应力的主要因素。

2) 钢靶板的运动对弹丸侵彻过程有重要影响：靶板的运动对弹丸速度的影响较小，但对弹丸出靶姿态有较大影响，尤其影响靶后运动姿态；靶板的运动对壳体应力具有一定的影响，弹丸的着靶姿态是影响壳体应力峰值主要因素之一。

[1] CORBETT G G，REID S R，JOHNSON W.Impact Loading of Plates and Shells by Free-flying Projectiles：A Review [J].Int J Impact Eng(0734—743X),1996,18(2):141-230.

[2] GOLDSIMTH W.REVIEW：Non-ideal Projectile Impact on Target[J].Int J Impact Eng(S0734—743X),1999，22(2)：95-395.

[3] HOU XIOFAN.GOLDSIMTH WERNER.Projectile Perforation of Moving Plates:Experimentel Investigation [J].Int J Impact Eng(S0734—743X),1996，18(7)：859-8755.

[4] DEY S，BOVIK T，HOPPERSTAD O S，et al.The Effect of Target Strength on the Perforation of Steel Plates Using Three Different Proiectile Nose Shapes [J].Int J Impact Eng(S0734—743X),2004，30(8)：1005-1038.

[5] 赵汝岩，卢洪义，曹亮.杆式动能体侵彻移动靶板数值仿真研究[J].弹箭与制导学报，2013,33(4):94-98.

[6] 薛鸿艳，王凤英，李长顺.动能弹斜侵彻运动装甲目标的数值模拟[J].弹箭与制导学报，2010,30(2):149-151.

[7] 陈振华，张国伟等.仿真分析三种射流形态对移动靶板的侵彻[J].弹箭与制导学报，2015,35(4):70-72.

[8] 吴广，陈赞，冯顺山等.钢靶运动对弹丸侵彻效应影响的仿真研究[J].系统仿真学报，2012，24(2)：198-503.

[9] 邹运，刘天生，刘敏娜.杆式动能弹斜侵彻横向运动靶板影响因索的数值模拟[J].弹箭与制导学报，201l，3l(6)：13l-134.

[10]史忠鹏，李惠元，孙立志.长杆弹垂直侵彻横向运动板的数值分析[J]装甲兵工程学院学报，2010，24(2)：4l-44.

[11]张晋红，刘天生.多层靶不同运动状态对高速球形弹侵彻的影响 [J].弹箭与制导学报，2013,33(5):91-94.

[12]BORVIK T,LANGSETH M.Ballistic penetration of steel plates[J].International Journal of Impact Engineering，1999，22(9/10)：855-866.

[13]史梁，沈培辉，薛建锋.弹体高速侵彻半无限钢靶的研究[J].兵工自动化，2016(1)：34-36.

(责任编辑 周江川)

Numerical Simulation of Anti-Warship ProjectilePerforating Moving Steel Plate Target

ZHANG Xue-lun，LIU Zong-wei，ZHANG Tuan，WANG Zhao-ming

(Chongqing Hongyu Precision Industrial Co., Ltd., Chongqing 402760, China)

Aiming to that anti-warship projectiles destroy moving targets, the process of anti-warship projectiles penetrating various compounding styles and moving state steel plates was simulated using nonlinear dynamic code LS-DYNA. The influence characteristics of single thickness, total thickness, moving state of steel plates on velocity change, attitude change and stress state of anti-warship projectile were analyzed. The numerical simulation results show that the total thickness of steel plates is the primary affect factor of velocity change, and single thickness of steel plates is the primary affect factor of velocity change and stress state, and the moving state of steel plates hardly affects velocity change and stress state, but markedly affects attitude change of anti-warship projectile.

anti-warship projectile; steel plate target; perforating effect; numerical simulation

2016-11-11；

2016-12-15 作者简介：张学伦 (1966—)，男，研究员级高级工程师，主要从事弹药工程的研究。

10.11809/scbgxb2017.04.007

张学伦，刘宗伟，张团，等.弹丸侵彻运动钢板的数值模拟[J].兵器装备工程学报，2017(4):32-36.

format:ZHANG Xue-lun，LIU Zong-wei，ZHANG Tuan，et al.Numerical Simulation of Anti-Warship Projectile Perforating Moving Steel Plate Target[J].Journal of Ordnance Equipment Engineering,2017(4):32-36.

TJ55

A

2096-2304(2017)04-0032-05