基于最优测试点的小波包隐马尔科夫模型故障诊断

鞠建波，胡胜林，祝 超

(海军航空工程学院，山东 烟台 264001)



【后勤保障与装备管理】

鞠建波，胡胜林，祝 超

(海军航空工程学院，山东 烟台 264001)

采用小波包变换和隐马尔科夫模型结合的方法，提出了机载通信电台的故障诊断模型。通过评价函数的建立，得到最优测试点集合；利用小波包变换提取测试点的能量特征值作为模型的输入，利用历史数据对隐马尔科夫模型进行训练，得到各个状态下的HMM参数，通过模式识别，实现电台的故障诊断；试验研究结果验证了所提出的方法的可行性和有效性。

故障诊断；最优测试点；小波包分析；隐马尔科夫模型；模式识别

对某型机载通信电台进行快速准确地故障诊断，及时的确定故障的位置和造成故障的原因，能够尽可能使其处于连续工作状态。随着保障技术的提高，传统的故障诊断方法由于时间长，工作量大，已经难以满足装备的保障要求，因此需要优化缩短诊断时间，减小工作量，对装备实现快速故障诊断。

本研究提出一种评价函数实现测试点的优化选择，减少测试工作量。在处理连续信号的长期研究中,小波包变换具有成熟的理论基础和应用背景。隐马尔科夫模型是一种由Markov链演变而来的强有力的模式识别方法。利用小波包分解[2]最优测试点集合上提取的信号特征作为隐马尔科夫模型[3]的输入，通过HMM模型完成模式识别，实现装备的故障诊断。

1 最优测试点选择

所谓最优测试点，就是利用系统的测试性[4]模型寻找测试点集合T的一个子集Ts[5]，使其测试代价最小，同时满足故障检测率(rFD)最大，虚警率(rFA)最小等测试性指标的要求。本研究通过对测试点建立评价函数实现测试点的优化选取。

某电台拥有n个测试点tn，所有测试点的集合为T,最优测试点[5]的集合为Ts,其测试点的故障检测能力为Pn，测试点测试结果的确定程度为Rn，则定义评价函数为

(1)

其中：ω为评价函数的参数；h(tn)与Pn和Rn成反比，即h(tn)越大，测试点tn被选择的概率越小。

通过上述评价函数[6]，可以得到更加优化的测试点集合，从而减少测试工作量，缩短工作时间，提高工作效率。

2 小波包变换

小波包变换是在小波变换的基础上提出的一种具有更精细的分解效果和更高的频率分辨率的信号特征值提取方法，解决了传统的小波变换在高频段分辨率低的问题。

对任意信号f(x)，小波变换的基本思想就是用一簇函数表示或逼近它，其小波变换可定义为

(2)

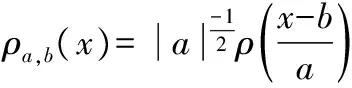
小波包分解得到的正交小波包基在频率上逼近希尔伯特空间，且它们的频率分辨率各不相同。给定正交尺度函数φ(t) 和小波函数ρ(t)，关系为：

(3)

(4)

其中，h0k,h1k是多分辨分析中的滤波器系数，继续递推得到：

(5)

由式(5)可知，ωn(t)是ω0(t)=φ(t)所确定的小波包[7]。

小波包变换把每个节点的信号分解成近似部分和细节部分两个部分，分别代表低频和高频。用小波包变换对信号进行三层分解，原信号、近似部分和细节部分分别用S，A1，D1代表，再将A1，D1进行分解，得AA2,DA2和AD2,DD2，依次类推，其结果如图1所示。

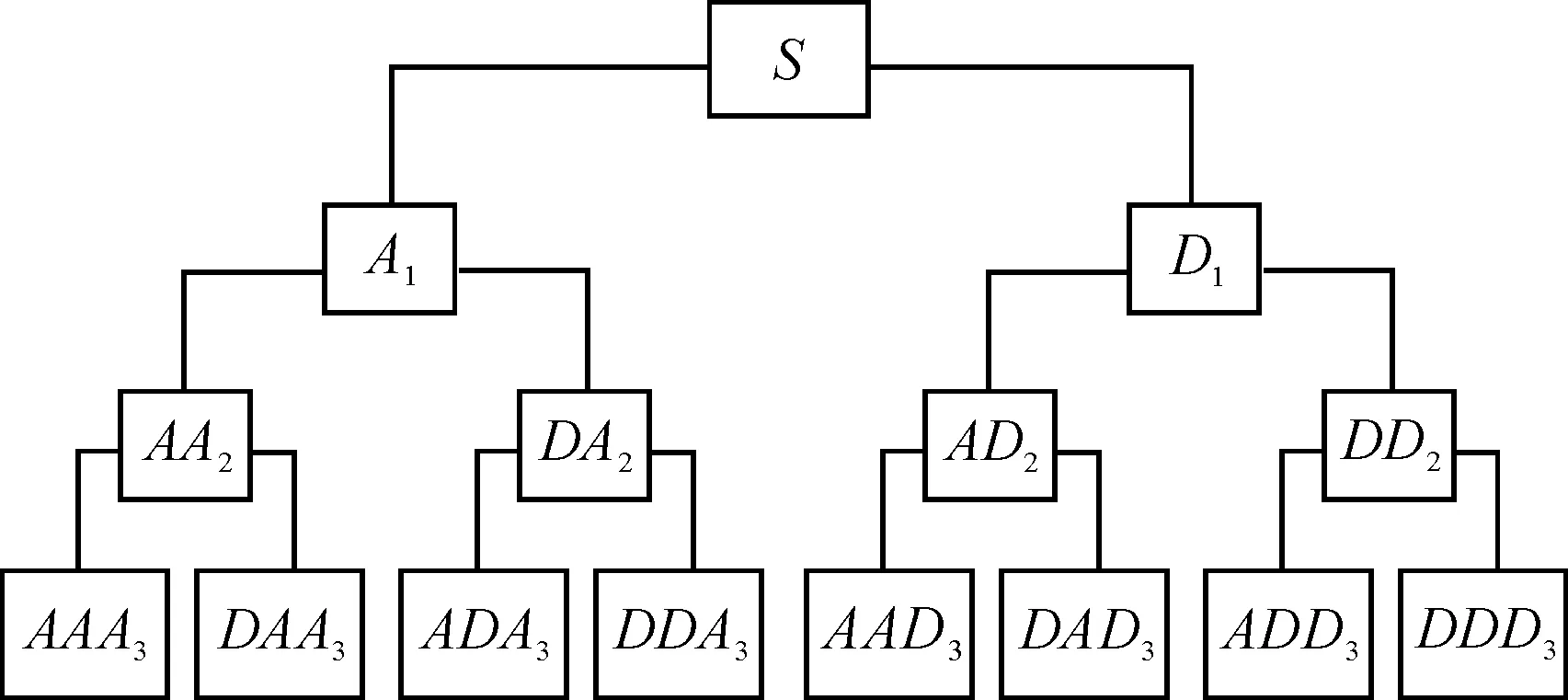
图1 三层小波包分解示意图

在进行能量信号特征值提取时，其能量定义为

(6)

其中cj,k(i) 是第j层节点上的第i个小波包系数。

3 隐马尔科夫模型(HMM)

HMM是由Markov链发展而来，是一种描述随机过程的概率模型，HMM是一个双内嵌式随机过程：其中一个随机过程是马尔科夫链,描述状态之间的随机转移；另一个随机过程描述每个状态和观测值之间的概率关系。观察者只能观察到与系统状态相关的观测值，而不能直接观测到隐藏的实际状态序列，其组成如图2所示。

HMM模型[7]可由下列参数描述：N表示模型中Markov链的状态数目，M表示每个状态对应的观测数目，π表示模型状态的初始概率分布矢量，A表示状态转移概率矩阵，B表示观测值概率矩阵。HMM模型记为λ=(π,A,B)。实际上，HMM可分为两部分：一部分是Markov链，由(π，A)描述状态之间的转移,产生状态序列；另一部分是一个随机过程，由B描述状态和观测变量之间的关系，产生观测值序列。

图2 HMM组成示意图

HMM基本算法解决的问题有3个：一是HMM的概率推理问题，利用前向算法和后向算法可得各个状态的似然概率P；二是最优状态序列的求解问题，利用Viterbi算法求出P最大时的状态序列；三是参数估计问题，利用B-W算法，对λ进行调整，使P最大，其重估公式为：

(7)

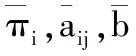
HMM方法用于装备故障诊断的具体做法是：选取最优测试点并获得能量信号，通过小波包方法去噪和能量特征提取。对处于正常态、轻度退化态和故障态的信号进行处理，获得信号特征值。然后利用B-W算法对其进行参数估计，得到各个状态下模型的状态转移概率。其过程如图3所示。

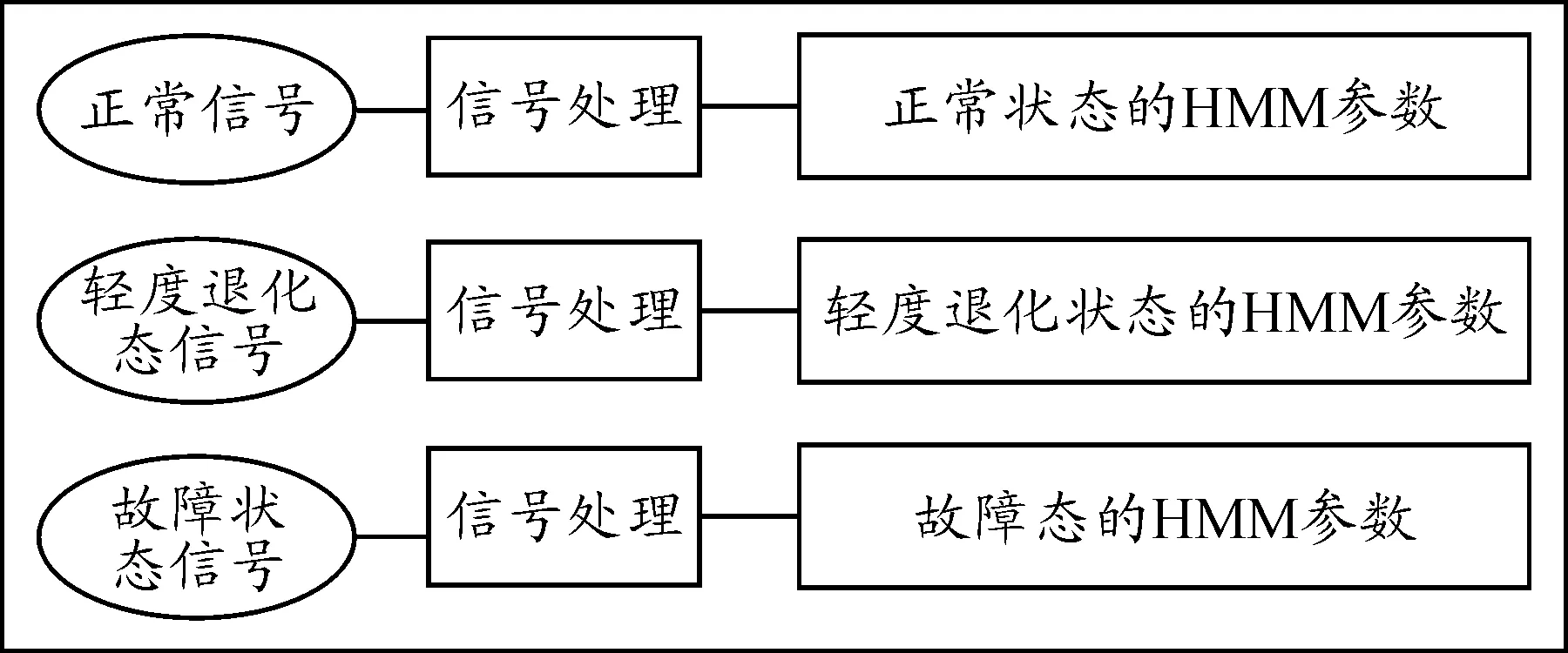
图3 HMM训练参数获取示意图

利用上述过程得到各状态的状态转移概率，再采用Viterbi算法对待测信号进行状态识别，通过建模与模式识别计算出各个状态的似然概率P。似然概率最大者，判断为该模块当前状态。

4 实例验证

4.1 诊断对象介绍

某型通信电台的接收部件主要由4个模块组成，有6个对外测试端口T1～T6。其信号流程图[8-9]和电台接受部件组成及功能如图4和表1所示。

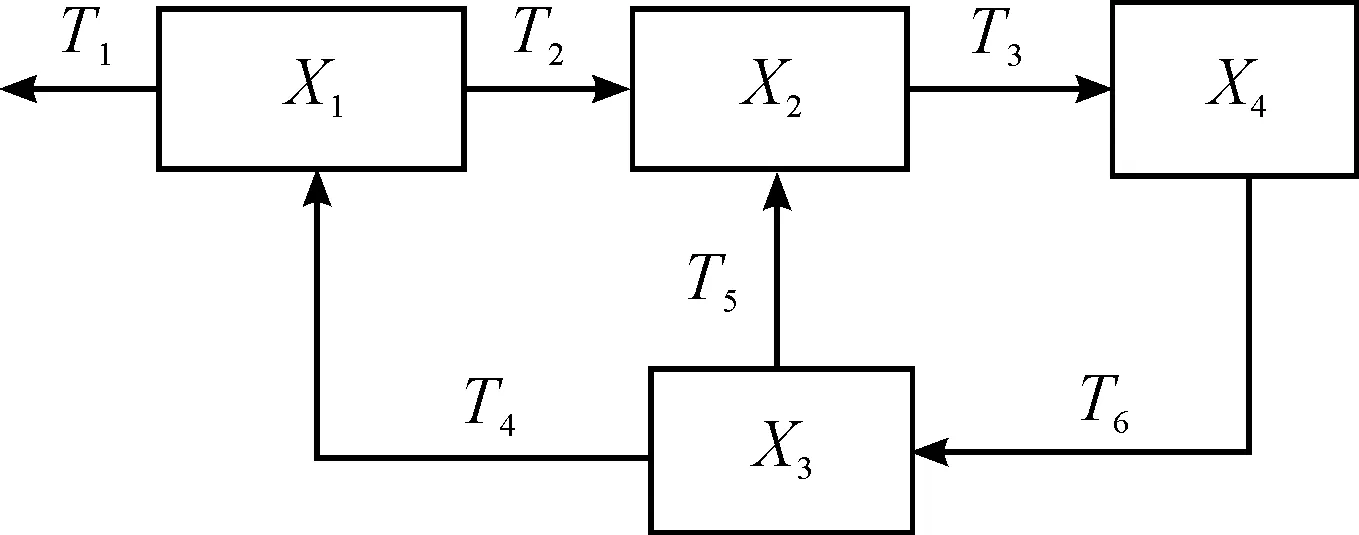
图4 某电台信号流程

本文对电台的接受部件故障诊断以主接收机模块(04模块)为例，该模块的功能为常规通信方式下，对信号放大、滤波、解调，完成接收全过程；在ECCM工作方式下为信号处理模块提供抗干扰的中频信号。其能量信号为连续的，能够很好地利用小波包对其进行特征提取。

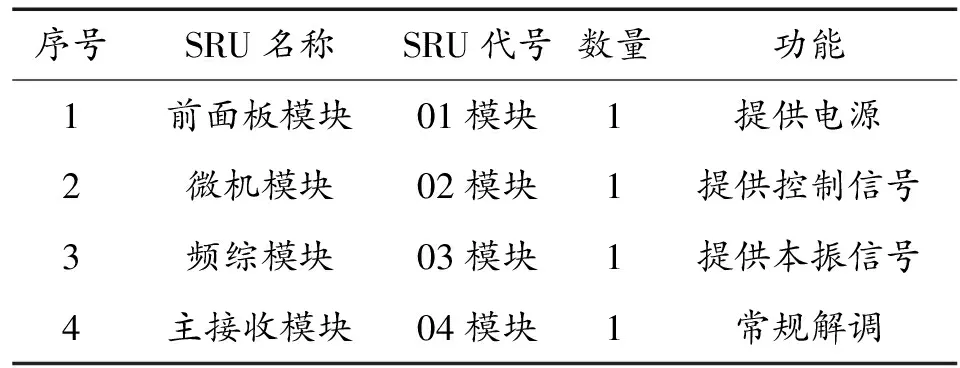
表1 电台主要SRU及其能

4.2 故障诊断

由历史数据可得6个测试点的测试结果确定性如表2所示。

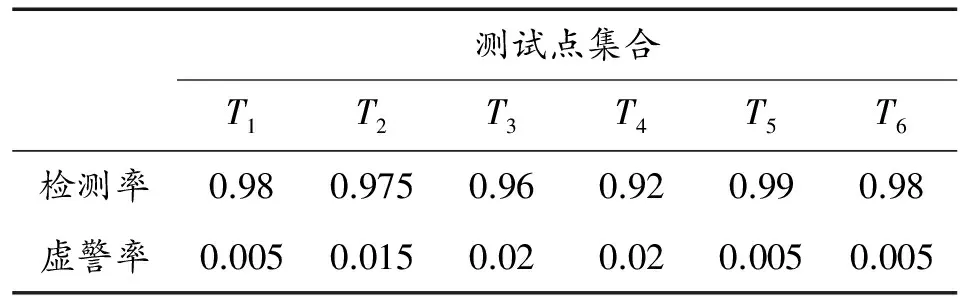
表2 测试点不确定集合

设评价函数的参数设为3，得各测试点的h(tn)，如表3所示。

表3 各测试点评价函数值

结果表明测试点T1/T2/T5/T6的评价函数h(tn)较小，选为最终的测试点。

从4个最优测试点进行数据采集，采集150个样本，采用小波包对每组样本进行三层分解，将第三层各节点的能量进行归一化处理，作为特征向量输入，选取前120个数据作为训练数据，分为3组，分别作为正常态，轻度故障态和故障态的训练样本，每组状态特征向量构成一条观测序列，训练HMM模型，从而获得各个状态的HMM参数值[10]。

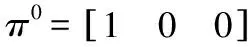
以上获得了HMM训练后的参数和转移概率矩阵和观测概率矩阵[11]。要实现故障诊断，只需要将某时刻的数据通过传感器采集，经过数据处理，特征提取，生成观测序列，然后输入训练好的各个模型进行测试，对输出的结果取对数。对数最大者，为当前模块所处的状态。

以第4个模块X4主接收机模块为例，测得其数据，通过流程，得到实验结果如表4所示。

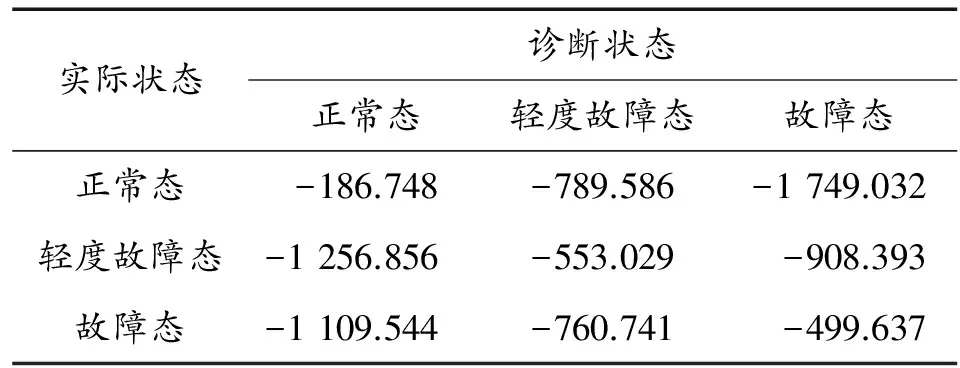
表4 主接收机模块的实验结果

以该模块的正常状态为例，它在各状态下的似然概率值最大为-186.748，故可判断模块当前处于正常状态，且该结果与模块的实际状态相符。其他同理可得。

[1] RABINER L R A.Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition[J].Proceedings of the IEEE,1989,77(2):257-286.

[2] NIKOLAOU N G,ANTONIADIS I A.Rolling Element Bearing Fault Diagnosis Using Wavelet Packets[J].NDTEInternational,2002,35(3):197-205.

[3] 胡海峰，安茂春，秦国军.基于隐Markov模型的故障诊断和故障预测方法研究[J].兵工学报，2009，30(1)：37-41.

[4] 邓森,景博.基于测试性的电子系统综合诊断与故障预测方法综述[J].控制与决策，2013，28(5)：641-649.

[5] PENG Y,DONG M,ZUO M J.Current status of machine prognostics in condition-based maintenance are view[J].The International Journal of Advanced Manufacturing Technology,2010,50(1):297-313.

[6] 蒋荣华.基于粒子群算法的电子系统可测性研究[D].成都:电子科技大学,2009.

[7] 肖文斌，陈进，周宇.小波包变换和隐马尔科夫模型在轴承性能退化评估中的应用[J]．振动与冲击，2011，30(8):32-33.

[8] 杨智勇,许化龙,许爱强.基于多信号模型的故障诊断策略设计[J].计算机测量与控制，2006，14(2):1616-1619.

[9] 龙兵，姜兴渭，宋政吉.基于多信号模型航天器多故障诊断技术研究[J].宇航学报，2004，25(5)：591-594.

[10]PENG Ying,DONG Ming.A Hybrid Approach of HMM and Grey Model for Age dependent Health Prediction of Engineering Assets[J]．Expert Systems with Application201，38(10):12946-12953.

[11]卓东风,原媛.小波包变换和隐马尔科夫模型(HMM)在液压系统故障预测中的应用[J].山西大学学报(自然科学版),2013,36(3):357-362.

(责任编辑 唐定国)

Fault Diagnosis System of Wavelet Packetand Hidden Markov Model Based on Optimal Test Point

JU Jian-bo, HU Sheng-lin, ZHU Chao

(Navy Aeronautics and Astronautics University, Yantai 264001, China)

By using wavelet packet transform and hidden Markov model, the fault diagnosis of airborne radio communication model was put forward. Through the establishment of the evaluation function, the optimal test set point was obtained. Using wavelet packet transform, we extracted the test point of energy eigenvalues for the input of the model, and the hidden markov model was trained using the history data, and we got the HMM parameters of each state, so as to realize the fault diagnosis of the radio by pattern recognition; Experimental results verified the feasibility and effectiveness of the proposed method.

fault diagnosis; optimal test poins; wavelet packet analysis; hidden Markov models; pattern recognition

2016-11-09；

2016-12-12

国家自然科学基金资助项目(60874112);军队科研专项资助项目(41512322)

胡胜林(1993—),男,硕士研究生,主要从事军事装备故障诊断研究。

鞠建波(1961—),男,教授,主要从事军事装备故障研究和水下目标探测与识别研究。

10.11809/scbgxb2017.04.020

format:JU Jian-bo, HU Sheng-lin, ZHU Chao.Fault Diagnosis System of Wavelet Packet and Hidden Markov Model Based on Optimal Test Point[J].Journal of Ordnance Equipment Engineering,2017(4):91-94.

TB114

A

2096-2304(2017)04-0091-04