考虑压电传感器漏电效应的大柔性智能结构建模方法研究

袁秋帆,刘延芳,朱东方,齐乃明

(1.哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001; 2.上海市空间智能控制重点实验室,上海 201109;3.上海航天控制技术研究所,上海 201109)



考虑压电传感器漏电效应的大柔性智能结构建模方法研究

袁秋帆1,刘延芳1,朱东方2， 3,齐乃明1

(1.哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001; 2.上海市空间智能控制重点实验室,上海 201109;3.上海航天控制技术研究所,上海 201109)

针对采用压电元件构成的大柔性智能结构基频较低、压电传感器漏电流效应明显而不能忽略等问题，对考虑压电传感器漏电流效应的结构建模方法进行了研究。推导了考虑压电传感器漏电效应的数学模型，根据等效电路，在传递函数中添加了一阶环节建立漏电流模型。搭建了压电型大柔性智能结构试验系统，用扫频测量技术获得了智能结构的幅频响应，用非线性最小二乘拟合的参数辨识方法计算了模型参数。通过分析试验数据，对比考虑和不考虑压电传感器漏电效应的智能结构模型的拟合结果，发现考虑压电传感器漏电效应的智能结构数学模型与实验结果吻合，尤其是在低频区域，验证了提出的智能结构数学模型的准确性。

大柔性智能结构； 压电传感器； 漏电效应； 参数辨识； 扫频； 非线性最小二乘拟合； 一阶环节； 低频

0 引言

随着空间科学技术的发展，大型化的大柔性结构在航天器中的应用日益广泛。大柔性结构的基频较低，其振动一旦被激发，衰减缓慢。大柔性结构的振动会影响航天器的姿态稳定精度，对载荷造成振动干扰，甚至会导致结构损坏、航天器失效。近年来，为减弱或避免大柔性结构的振动，提出了主动振动控制技术，采用智能元件与大柔性结构整合形成智能结构实现振动抑制[1]。

智能结构数学模型的精确度直接影响振动抑制控制器设计的优劣，从而影响振动抑制的效果。对压电型智能结构的建模方法，已有文献提出了多种方法。柔性结构具无穷阶谐振模态，是一个分布参数系统，每阶模态都可用偏微分方程描述[2]。对挠性结构建模时，忽略结构带宽外的振动模态对结构整体振动的影响虽简化了控制器设计，但这些忽略的振动模态会影响系统传递函数的零点，导致设计的闭环控制系统不稳定。因此，文献[3]在系统传递函数中引入了馈通项作为对其的补偿。现有的研究中，智能结构的基频均较高(1 Hz以上)，压电式传感器在1 Hz以上的频率区间内，对振动的测量准确，效果较好[4]。在低频条件下，压电传感器特性不理想，漏电流效应(电荷泄露)较明显，在进行准静态校准时，就必须考虑漏电流效应[5-8]。但在对大柔性压电型智能结构建模时，目前尚无文献考虑漏电流效应。大柔性结构基频较低，对测量其频率的压电传感器进行建模时，若不考虑压电元件的漏电流效应，则数学模型将产生较大误差。本文针对压电型大柔性智能结构，考虑压电传感器的漏电流效应，给出了数学建模方法。采用参数辨识技术，通过实验测量和对比，对提出的大柔性智能结构数学模型的准确性进行验证。

1 大柔性智能结构数学模型

薄板大柔性结构是典型的大柔性结构，如航天器的太阳能电池阵、大型阵面天线等。本文以薄板结构为例进行压电型大柔性智能结构的建模研究。

悬臂薄板如图1所示。采用贴压电陶瓷片构成大柔性智能结构时，常采用同位粘贴[9]。即压电执行器和压电传感器对位分别贴于薄板结构两侧，薄板表面任意位置(xi,y0) 处两个侧面分别贴有压电传感器(Si)p个和压电陶瓷执行器(Ai)1个，压电元件施加在薄板上的载荷等效为力矩M(x，t)。

1.1 压电执行器模型

压电执行器的原理是逆压电效应，在压电片式执行器两个表面电极上施加电压，会在其主方向上产生应变，从而对柔性板产生弯矩的作用。第i个执行器上的电压Va,i(t)与产生弯矩满足关系

(1)

(2)

式中：Eb，Ib分别为薄板的杨氏模量和横截面惯性矩；ρb为薄板x方向线密度；p为执行器数量[10]。

将式(1)代入式(2)，并考虑薄板的阻尼，得

(3)

1.2 压电传感器模型

不考虑漏电流效应时，压电传感器利用压电效应，当传感器发生应变时，传感器上下表面的电极会产生电荷，通过线性电荷放大器，得到电压模拟量，从而测量得到传感器处的平均应变。压电传感器有一个主方向，其上电荷量的变化与主方向上的应变成正比。如图2所示，压电传感器的主方向为x向，即柔性板的长度方向。

压电传感器产生的电荷量与应变关系可表示为

(4)

式中：d31为压电常数；Ep，hp，lp分别为压电陶瓷片的杨氏模量、宽度和长度；εi为压电陶瓷片在x向上的应变。

由基尔霍夫梁假设，可得应变与挠度关系

(5)

式中：tb，tp分别为薄板和压电陶瓷片的厚度。

将式(5)代入式(4)，得

(6)

设电荷放大器增益为gc，则电荷放大器输出电压与模态坐标间的关系为

(7)

考虑漏电流效应时，压电传感器的基本电路原理如图3所示[5，11]。

压电传感器受到应力产生电荷时，压电传感器内部就构成了一个RC电路，为一阶惯性环节，漏电时间常数τL=CsRs。此处：Cs为等效电容；Rs为等效电阻。传递函数可表示为

(8)

式中：gL为增益。

综上，当考虑压电传感器漏电流效应时，传感器的数学模型为

(9)

1.3 大柔性智能结构传递函数描述

根据压电执行器和传感器的数学模型，应用薄板振动基本方程和哈密顿原理，结合文献[12]给出的数学模型，不考虑压电元件的漏电流效应，从压电执行器上的输入电压至压电传感器的输出电压的传递函数为

(10)

式中：Φk=[ψk,1ψk,2…ψk,i…ψk,p]T。

为获取可用的数学模型，将模态截断到第N阶，直接截断有可能出现外溢现象，从而导致控制系统不稳定。结构带宽内高于N阶的模态可用馈通项近似，则控制系统开环传递函数可表示为

(11)

式中：gvv=gLgsga；D为馈通项，又称为模态截断误差[13]。若考虑压电传感器的电荷泄露，则控制系统开环传递函数可表示为

(12)

2 大柔性智能结构试验分析

2.1 大柔性智能结构振动测量试验系统组成

压电智能结构的基本组成如图4所示。其中：压电传感器和压电执行器为压电陶瓷元件。压电传感器采集的电荷通过电荷放大器线性转换为电压值，经模数转换(AD)模块，计算机采集到压电传感器的测量值，以电压表示。计算机为主动振动抑制控制器，根据压电传感器的测量值，计算控制量，并通过数模转换(DA)模块，经功率放大器放大，输出电压至压电执行器，压电执行器产生一定的伸缩应变，从而产生应力，实现主动振动抑制控制。

柔性板如图5所示，悬臂固定于基座上，为降低板的第一阶模态频率，在板的端部添加集中质量块。在柔性板根部，对位粘贴两对压电陶瓷片，分别为S1/A1和S2/A2；在板的一侧，粘贴的是S1，S2(传感器)，则在对侧，对应的是A1，A2(执行器)。

2.2 压电传感器漏电流时间常数测量

可用阶跃响应的方法测量压电传感器的漏电时间常数，如图6所示。具体方法为：在板静止状态下，在距离板端部l0处放置挡板，对板端部施加力，使板变形至挡板位置，即对压电传感器近似输入一个阶跃信号，采集压电传感器的反馈，即能获得压电传感器的阶跃响应。

测量并绘制压电传感器测量电压随时间变化的曲线，结果如图7所示。根据阶跃响应，可算得时间常数τ=0.51 s。

2.3 大柔性智能结构模型参数辨识方法

薄板振动变形量为小量，多个执行器施加电压对单个传感器测量电压的影响满足叠加关系。同位控制时，设压电执行器/传感器对有m对，则第i个执行器施加电压到第j个传感器测量电压的传递函数可表示为

(13)

开环传递函数中未知参数有gvv，τL，ψk,i，ψk,j，Dij，ζk，ωk，gvv，τL。用参数辨识方法获取这些参数时，需要结构的频率响应数据，这可用扫频的方法得到结构的频率响应。在第i个执行器上加载扫频信号电压Vi，其信号形式为

(14)

式中：K为增益；vω为频率增加速度，且vω∈R；ω0为扫频初始频率。采集p个传感器的电压输出，令第j个传感器上的输出电压为Vs,j，对其进行快速傅里叶变换(FFT)，得到Vs,j在频域上的信号描述fVs,j。则由第i个执行器输入电压到第j个传感器输出电压的频率响应为

(15)

由此，则求解传递函数参数问题转为以下数学问题：已知函数形式为

(16)

当函数自变量s=Vi时，函数值为Gij，求解式(16)中ψk,j，ψk,i，Dij，ζk，ωk，gvv，τL的值。

选取价值函数

(17)

式中：‖ ‖表示复数的模。用非线性最小二乘拟合方法，使价值函数为最小，得到ψk,j，ψk,i，Dij，ζk，ωk，gvv，τL。从而得到由p个执行器输入电压至p个传感器输出电压的传递函数。

2.4 模型参数辨识试验

设扫频信号频率范围(0.01，1.5) Hz，信号长度1 800 s，则FFT变换结果如图8所示。用扫频方法测得传感器的测量结果如图9所示。

对测量数据进行FFT变换，得到幅频响应曲线如图10所示。

由传感器测量值的幅频响应可知：在扫频0.01～15 Hz范围内，共有2个共振频率(0.80，9.53 Hz)，分别对应挠性柔性板的第一阶面外弯曲模态和第二阶面外弯曲模态。

2.5 试验数据分析

根据大柔性智能结构传递函数的数学模型，若不考虑压电传感器漏电效应，数学模型可描述为

(18)

基于式(17)给出的价值函数，分别采用考虑和不考虑压电传感器漏电效应的数学模型，采用最小二乘拟合的方法，拟合得到式(16)、(18)中的ψk,j，ψk,i，Dij，ζk，ωk，gvv，τL的值，结果分别见表1、2。拟合结果分别如图11～16所示。

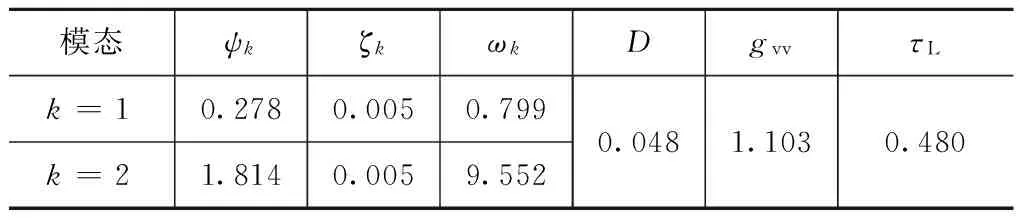
表1 考虑压电传感器漏电效应的数学模型参数Tab.1 Parameters of mathematical model considering leakage effect of piezoeleectric sensor

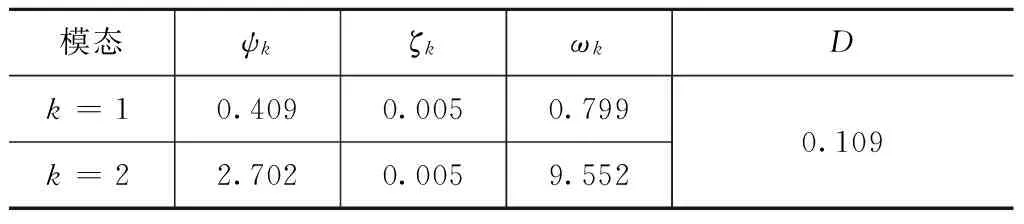
表2 不考虑压电传感器漏电效应的数学模型参数Tab.2 Parameters of mathematical model not considering leakage effect of piezoeleectric sensor

由图11～16可知：当频率大于0.5 Hz时，拟合效果较好，压电传感器的漏电效应产生的影响小，在一阶和二阶模态频率处，两种数学模型均有较好的拟合结果；在小于频率0.5 Hz的低频段，由于压电传感器漏电流的影响，幅频响应幅值随扫频频率降低而逐渐减小。比较发现，在频率低于0.5 Hz的范围内，用式(18)描述的数学模型是不准确的，而式(16)可准确反映低频情况，得到的拟合曲线拟合度为0.984 0，表明式(16)给出的数学模型较准确。

3 结论

针对大柔性智能结构基频较低，压电传感器漏电流效应明显，不能忽略的问题，本文首先推导了考虑压电传感器漏电效应的数学模型，搭建了压电型大柔性智能结构试验系统，用扫频测量技术获得了智能结构的幅频响应，用非线性最小二乘拟合方法获得了模型参数。通过对试验数据分析，对比考虑和不考虑压电传感器漏电效应的智能结构模型的拟合结果，所提出的考虑压电传感器漏电效应的数学模型较准确地描述了大柔性智能结构特性，提出的数学模型和建模方法可用于大挠性智能结构主动振动控制等领域，提高低频状态下主动振动控制器设计的准确性，有潜在的应用前景。

[1] 黄文虎, 王心清, 张景绘, 等. 航天柔性结构振动控制的若干新进展[J]. 力学进展, 1997, 27(1): 5-18.

[2] 陆佑方. 柔性多体系统动力学[M]. 北京: 高等教育出版社, 1996.

[3] MOHEIMANI S O R, ANDREW J F. Piezoelectric transducers for vibration control and damping[M]. Berlin: Springer, 2006: 9-66.

[4] 李东旭, 刘望, 蒋建平, 等. 空间智能桁架的传感器作动器位置优化和分散化自适应模糊振动控制[J]. 中国科学: 技术科学, 2011, 41(5): 605-606.

[5] 章劲秋, 孔德仁, 王芳, 等. 压电式压力测量系统准静态校准压力脉宽分析[J]. 测控技术, 2016, 35(6): 121-128.

[6] 何建中, 周贻洁. 压电传感器二次仪表——电荷放大器的准静态特性研究[J]. 华东工业大学学报, 1995, 17(2): 28-32.

[7] 杨凡, 孔德仁, 孔霖, 等. 压力电测系统的静态及准静态校准适用性探讨[J]. 测控技术, 2016, 35(5):129-136.

[8] 吴晓娜, 侯小兵. 扩展压电传感器频率响应范围的方法研究[J]. 电子测量技术, 2015, 38(6): 100-103.

[9] 陈勇, 陶宝祺, 刘果, 等. 柔性结构振动控制的初步分析与试验研究[J]. 机械强度, 1998, 20(3): 208-209.

[10] MEIROVITCH L. Elements of vibration analysis[M]. 2nd Edition. Sydney: McGraw-Hill, 1996.

[11] MOHEIMANI S O R, BEHRENS S. Multimode piezoelectric shunt damping with a highly resonant impedance[J]. IEEE Transactions of Control Systems Technology, 2004(3): 484-491.

[12] PETERSEN I R, LANZON A. Feedback control of negative imaginary systems[J]. IEEE Control Systems Magazine, 2010, 30(5): 54-72.

[13] HALIM D, MOHEIMANI S O R. Reducing the effect of truncation error in spatial and pointwise models of resonant systems with damping[J]. Mechanical systems and signal processing, 2004, 18: 291-315.

《上海航天》征稿简则

《上海航天》已列入中国知网、万方、超星、维普等数据库，是宣传航天技术发展、科研成果的重要窗口，主要刊登有关卫星、火箭、载人飞船、深空探测、导弹等系统及其分系统的预先研究、研制、试验及工程实践等方面的科技论文，同时介绍相关新概念、新方法、新技术及理论探讨。

一、征稿范围

稿件内容以研究论文与报告、技术交流、专题综述等形式为主，广泛报道航天重点专业的理论创新，学术研究，工程实践，创新与探索，学术争鸣，战略发展与情报研究，产学研成果等。

二、写作要求

1. 来稿应突出航天理论研究和技术创新性，兼顾工程应用，应给出相应的理论依据、参数确定原则。论文应注重理论性、新颖性、逻辑性，避免写成技术报告。

2. 来稿内容充实，论点明确，论据充分，层次分明，文字简练，字数一般以5 000～6 000字为宜(情况特殊可超出)。

3. 禁止学术不端行为和一稿多投。投稿时作者应对文章作非密处理，在最终修改稿完成后应提供保密审查证明的扫描件或纸质原件。

5. 凡国家、省、部级科技进步奖课题论文，自然基金、重点攻关项目论文，请提供项目编号或获奖证书复印件，可提前安排发表。

6. 来稿应包括题目、作者姓名、单位、摘要、关键词、作者简介、正文、参考文献著录。题目一般不超过20个汉字。摘要(200～300字)说明研究目的、方法、结果或结论等。关键词5～8个。参考文献尽量在10篇以上，并在正文中标出引用处。请提供题目、作者、单位、摘要、关键词、图题和表题的英译文。

7. 作者简介包括姓名、出生年、最终学历和职称、主要研究方向或从事工作。

8. 正文包括引言、主体、结论或结束语部分。引言说明关于研究历史、现状、存在的问题及本课题的着眼点和新进展及创新点。主体要求语言简洁、明确、准确无歧义，表达单刀直入，逻辑关系完整，结构严谨。结论或结束语对研究内容进行总结。

9. 量和单位符合国家标准。每个量符号第一次出现时应给出物理意义说明，同一符号只能表示一个物理量，必要时可用下标区分。一般变量为斜体，矢量、矩阵、张量、向量为斜黑体。单位一般为正体。

10. 公式用公式编辑器输入。仅重要或文中引用的公式才需编号。

11. 正文中给出图表的引文。图数量一般不超过12幅，尺寸尽量小于8 cm。图中文字、数字、符号清楚，横纵坐标的变量名、单位、刻度值准确完整，不同线型或图符有说明。图可在Word或Visio中解组、修改。表格栏头简化，避免斜线，不能空白；项目栏中文字简练；栏内尽量不要出现公式；各格内上下左右格内容相同时不能用"同左"、"同右"、"同上"，或" "，无内容时不能空格，要用一字线补齐。图表中的量和单位采用“量/单位”方法标注。

12. 文中外文缩写第一次出现时给出中文全称。

13. 引用文献遵循“最新、关键、必要”的原则，在正文中顺序引述，未公开发表资料不引用。文献著录格式参考国家标准《文后参考文献著录规则》。主要如下：

专著 姓名. 书名[M]. 版本(第1版不写). 出版地: 出版者, 出版年: ××-××(页).

期刊 姓名. 题名[J]. 刊名, 出版年, 卷(期): ××-××(页).

报告 姓名. 题名[R]. 报告名称, 编号, 出版时间.

会议录 姓名. 题名[C]// 会议名称. 会议地点(城市): 出版者, 出版年: 起止页码.

标准 标准起草者. 标准名称[S]. 标准发布者, 标准号, 出版年.

学位论文 姓名. 题名[D]. 出版地: 出版者, 出版年.

三、联系方式

来稿时请提供Word电子文档，并请附上详细通信地址、E-mail邮箱、手机号。查稿电话：(021)24181441。投稿网站：http://shht.ijournal.cn。

《上海航天》杂志编辑部

Study on Modeling Method of High Flexible Intelligent Structure Considering Leakage Effect of Piezoelectric Sensor

YUAN Qiu-fan1, LIU Yan-fang1, ZHU Dong-fang2, 3, QI Nai-ming1

(1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, Heilongjiang, China;2. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;3. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

For the problems of high flexible smart structure composed of piezoelectric components which had low nature frequency and obvious leakage effect of piezoelectric sensor not being neglected, the modeling method of the structure considering leakage effect of piezoelectric sensor was studied in this paper. A mathematical model of high flexible smart structure with considering the piezoelectric sensor leakage effect was established. According to the equivalent circuit, a first order damp element was added into the model to build the leakage model. An experiment system was built and the amplitude frequency response of the structure was obtained through the sweep frequency technique. The parameter identification method was used to calculate the model parameters by nonlinear least squares fitting. Based on the analysis of the experimental result, the models with and without considering the leakage effect were compared. It found that the model with considering the leakage effect were agreed with the experimental result, especially in low frequency range. The proposed model is verified and it is a more accuracy model.

high flexible smart structure; piezoelectric sensor; leakage effect; parameter identification; sweep-frequency technique; nonlinear least squares fitting; first order damp element; low frequency range

1006-1630(2017)02-0177-07

2017-01-22；

2017-03-31

中央高校基本科研业务专项资金资助(HIT.NSRF.201622)；微小型航天器技术国防重点学科实验室开放基金资助(HIT.KLOF.MST.201507)

袁秋帆(1992—)，男，博士，主要研究方向为挠性结构动力学。

刘延芳(1986—)，男，博士后，讲师，主要研究方向为飞行器动力、制导与控制、智能材料动力学与控制、空间柔性机构展开动力学与控制等。

O482.41

A

10.19328/j.cnki.1006-1630.2017.02.020

被《中国学术期刊

总库》及CNKI系列数据库、万方数据库、超星数据库、维普数据库等收录，作者著作权使用费与本刊稿费一次性给付。如作者若不同意文章被收录，请在来稿中予以说明，本刊将做适当处理。