基于μ综合的新型空空导弹稳定控制系统控制律设计研究

刘 慧,张佳梁,邵长兴,张 迪

(上海机电工程研究所,上海 201109)



基于μ综合的新型空空导弹稳定控制系统控制律设计研究

刘 慧,张佳梁,邵长兴,张 迪

(上海机电工程研究所,上海 201109)

为避免控制律设计结果出现较大的保守性，考虑新一代大机动空空导弹的非线性、各通道的耦合作用、不确定性和未建模动态特性等问题，研究了基于μ综合方法的导弹稳定控制系统控制律设计。建立了某空空导弹的俯仰通道模型，给出了控制律结构、权函数设置与选取、控制律设计指标，对未建模不确定性、参数不确定性和传感器测量噪声进行了建模，设计了控制结构，用D-K迭代获得了μ综合控制器。数字仿真验证结果表明：设计的俯仰通道鲁棒控制器满足控制性能指标要求，有良好的鲁棒性与稳定性，对大机动空空导弹的非线性、各通道的耦合作用、不确定性和未建模动态特性等具良好的控制效能，实现了一个控制器控制多个工作点，突破了经典控制系统中一个控制器控制少数几个工作点，需在飞行包络内进行复杂动态调参的传统控制模式。

空空导弹； μ综合； 鲁棒； 稳定控制系统； 不确定性； 俯仰通道； 控制律； D-K迭代

0 引言

由于技术水平所限，早期的空空导弹机动能力差、使用范围窄，主要攻击轰炸机和机动性能较差的歼击机，当时空空导弹的稳定控制系统多采用结构较简单、物理概念明确的经典控制理论设计，在弹体模型参数摄动较小时，能获得较满意的效果。但空空导弹的运动模型本质上是一个十分复杂的非线性变参数模型，传统线性方法在设计空空导弹的控制系统时，导弹数学模型通常在被基于参数固化和小扰动等假设条件下进行简化，导致存在以下两个问题[1]。一是对非线性系统的未解耦小偏差线性化处理。传统空空导弹控制系统设计中参数固化和小扰动两个假设，将导弹运动模型作线性化处理，忽略了导弹运动的非线性和各通道间的耦合作用，难以解决多个通道参量快速变化产生的问题。二是对系统的不确定性和未建模动态的处理。传统控制系统是根据标称模型设计的，但实际模型往往存在不确定性和未建模动态特性，随着高性能空空导弹的出现，导弹模型中非匹配和不确定性的特点越来越突出。在存在参数摄动、外部干扰时，传统的频域及PID控制方法已越来越难保证系统的鲁棒性[2]。为在现代高科技战争中取得技术优势，新一代空空导弹进行了全面技术改进，显著提高了其作战性能，如增大作战空域与飞行包络、提高速度特性与机动性能、增加推力矢量装置等。此时用传统经典控制理论设计的稳定控制系统则出现了因导弹模型线性化处理而忽略的非线性特性、各通道间耦合作用、对象特性的不确定性和未建模动态特性等问题，导致设计的导弹稳定控制系统鲁棒性严重不足，极大地限制了导弹的作战使用范围[3-4]。为解决上述问题，本文采用鲁棒控制理论与方法进行新型空空导弹稳定控制系统的控制律设计。这种方法通过合理的评估和建模，可将忽略的导弹的非线性、各通道耦合作用、不确定性和未建模动态特性等加入控制律的设计过程[5]。鲁棒控制理论体系的两个主流分支是H∞控制理论与μ综合控制理论。为避免控制律设计结果出现较大的保守性，本文采用μ综合控制理论设计控制律，对某空空导弹俯仰通道稳定控制系统的μ综合控制律设计进行了研究[6]。

1 μ综合与D-K迭代

1.1 μ综合标准控制问题

标准μ综合控制问题的线性分析描述如图1所示[7]。图1中：P为系统的开环联连，包含标称对象模型、不确定性模型、性能和不确定性加权函数等所有已知的环节；Δ为范数有界的结构化不确定性集合(表征被控对象的不确定性)；K为控制器。其中：P的输入有摄动p、扰动d、控制u；输出有摄动w、误差e、测量输出y。被控系统集可用线性分式变换(LFT)形式描述为

(1)

(2)

此性能指标包含了图1所示的线性分式变换Fl(P，K)的鲁棒性能检验[8]。为评价闭环系统的鲁棒性能，定义一个增广摄动矩阵

(3)

(4)

式中：ω为角频率。

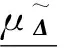
(5)

(6)

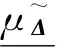
(7)

(8)

1.2 D-K迭代

目前，μ综合的有效近似方法是D-K迭代，它包括以下两步迭代过程[6]。

a)保持D(s)不变

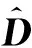
b)保持K不变

D-K迭代法的流程如图3所示。

2 导弹弹体对象分析

2.1 导弹弹体俯仰通道模型

在某一特征点上，对导弹的非线性模型线性化，可得弹体的俯仰小扰动线性化模型

(9)

式中：xlon=[uwqθ]T；Alon，Blon，Clon，Dlon为导弹俯仰通道模型的状态方程矩阵；ulon为升降舵偏角，即ulon=δe；ylon=[αzαuwqθ]T。此处：αz，α分别为机体坐标系中z轴向的线加速度分量和攻角；u，w，q，θ分别为弹体坐标系中x轴向的速度分量、z轴向的速度分量、俯仰角速率和俯仰角。

某空空导弹典型弹道的俯仰通道部分特征工作点见表1。各工作点奇异值如图4所示。可发现：包线内各工作点的俯仰通道模型固有频率在区间[3.656 5，26.992 6] rad/s内的变化范围很大。导弹的固有频率主要取决于转动惯量、静稳定度和动压[10]。忽略转动惯量的变化，当高度变化不大时，固有频率的变化主要取决于静稳定度和速度变化。对俯仰通道，全包线内攻角与马赫数的大范围变化使弹体静稳定度变化剧烈，且随之而来的是全包线内操纵性也变化很大[11]。对此，将静稳定性导数及操纵性系数的不确定性引入稳定控制系统的控制律设计中，可显著改善剧烈变化的静稳定性及操纵性对驾驶仪鲁棒性的影响，从静稳定性及操纵性等方面改善驾驶仪的鲁棒性。

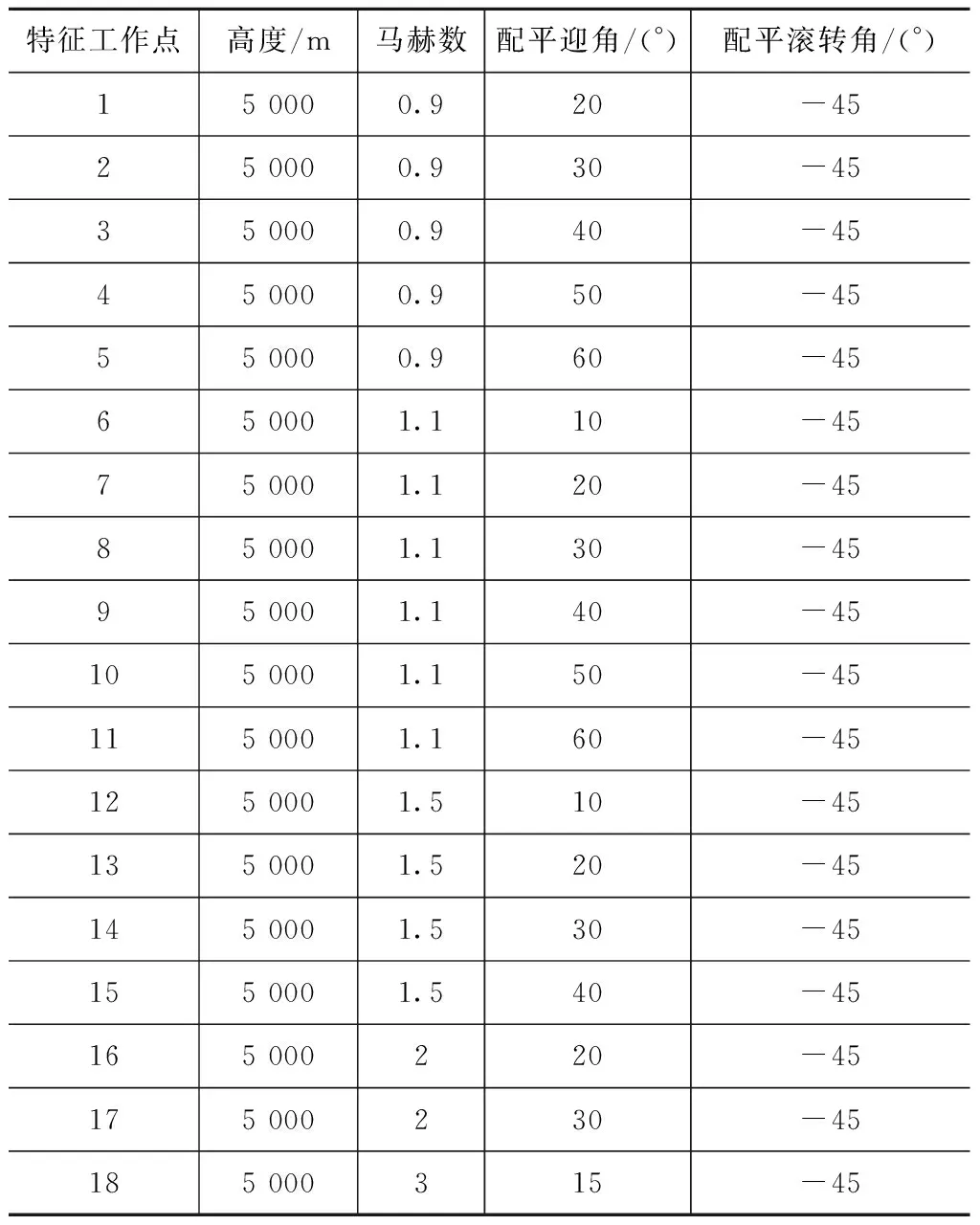
表1 某空空导弹某弹道包线采样工作点及配平Tab.1 Sampling point of envelope curve of some air-to-air missile’s trajectory and its trim

另外还可发现：大部分工作点短周期的阻尼比不足，说明在控制律设计时需采取措施对短周期模态进行增稳。为此，可将俯仰角速率信号q反馈至控制器，以改善短周期模态阻尼。

2.2 不确定性

2.2.1 未建模不确定性

稳定控制系统是基于典型弹道上某特征工作点的数学模型(称为名义模型)设计的，但该数学模型是通过对导弹的非线性时变弹性模型进行一系列的简化假设和线性化处理而得的，因此名义模型与对应特征点的导弹实际模型间存在未建模动态特性不确定性[12]。基于文献[13]，本文对俯仰通道模型的未建模不确定性预估为：在低频段(0.1 rad/s附近)，模型误差为40%；在高频段(100 rad/s附近)，模型误差为100%。

2.2.2 参数不确定性

本文中参数不确定性是源于风洞实验误差的气动系数不确定性最终体现在模型中的参数不确定性[14]。对本文中俯仰通道线性弹体模型，气动系数多体现在Alon，Blon中，故分析各工作点中Alon，Blon阵的不确定性，能一定程度说明气动系数在全包线内的变化。统计包线内Alon，Blon的数值，可发现各参数出现不同程度的变化，其中Alon(1，2)，Alon(3，1)，Alon(3，2)，Blon(1)的变化最剧烈，需将这4个参数的不确定性引入控制律设计，才能提高控制系统鲁棒稳定性(但参数的不确定性范围应视鲁棒性与鲁棒稳定性权衡决定)。控制设计中需选取一组典型的工作点作为标称系统，进行控制器设计，从Alon，Blon的数值统计中也可确定与平均值最接近的一组工作点作为标称系统。

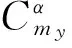
(10)

此时式(10)中并未直接反映攻角与俯仰力矩的关系，但俯仰力矩与俯仰角加速率成正比，可推导攻角与俯仰角加速率的关系：当β=0时

(11)

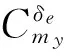
2.2.3 传感器噪声

本文中俯仰通道稳定控制系统所用的传感器主要有加速度计与角速率陀螺，则测量噪声分别为加速度计噪声与角速率陀螺噪声。结合文献，估计加速度计噪声为0.1%，角速率陀螺噪声0.5%[10]。

3 控制律设计

3.1 控制策略

3.1.1 控制律结构

从控制系统来看，导弹有内回路(稳定控制回路)和外回路(制导控制回路)两个基本控制回路。本文主要设计导弹的内回路。稳定控制回路的常用结构有过载控制结构和姿态控制结构两种[15]。

本文俯仰通道采用了过载控制结构。根据对象，为改善短周期模态阻尼，需将角速率信号反馈回控制器。综上，设计控制律结构为

(12)

式中：Klon为俯仰通道控制器矩阵；Azm，Azc分别为过载指令及导弹过载反馈；q为俯仰角速率。

3.1.2 权函数设置与选取

鲁棒控制理论中的权函数与经典控制理论中的增益类似，在控制系统设计时，通过不断调节权函数或增益，以获得期望的控制系统性能。但不同的是，经典控制中的增益物理概念不明确，需通过根轨迹等方式分析其对控制系统性能影响，从而确定调节方向，且增益最终是作为控制器组成部分。权函数的物理概念非常明确，针对性强，在一个典型鲁棒控制系统中的权函数有用于限制控制信号幅值、调节控制器带宽、规范化未建模不确定性，以及调节控制系统跟踪性能的等。权函数只存在于控制系统的设计中，并不在最终的成品控制系统中。

权函数的设置取决于对控制系统性能的期望，本文基于鲁棒控制理论实现。针对新型空空导弹的需求，经典控制方法的缺陷是因导弹模型的线性化处理而忽略的非线性，以及高性能导弹系统越来越突出的不确定性与未建模动态特性。因此，本文控制律设计中的权函数设置需解决上述问题，同时也要体现控制律的控制效用。由此，权函数的设置方案可概括为：

a)设置用于限制控制信号幅值或外部扰动的权函数；

b)设置用于规范化未建模不确定性的权函数；

c)因本文的控制律设计是针对导弹的飞行控制系统的，而飞行控制系统的作用是控制跟踪过载或姿态信号，故还需设置调节跟踪性能的权函数。

权函数的选取直接决定控制系统性能的优劣。如用于规范化的权函数，多决定了控制系统的鲁棒性能，而调节控制效力的权函数则决定控制系统的快速性、稳定性、准确性等基本性能。一般，鲁棒控制系统中的权函数可为两大类：一类是用于规范化的权函数；一类是调节控制效力的权函数，通常称为性能权函数。根据已有的设计经验，两类权函数的选取依据和法则如下[16-18]。

a)规范化权函数

是指对相应的环节(可以是不确定性、扰动信号、控制信号等)起到规范作用的权函数。如图5中，Δ为被控对象G的输入端不确定性，因不确定性在加入鲁棒控制系统设计中时需满足‖Δ‖∞<1，而控制案例中的不确定性常不满足此要求，故需用权函数W规范化Δ，使之满足条件。具体方法为：选取权函数使‖W‖∞>‖Δ‖∞，并令Δ′=Δ/W，则此时Δ′即能满足‖Δ′‖∞<1。

b)性能权函数

性能权函数的作用是调节控制系统的控制效力，如本文的飞行控制系统是一个跟踪系统，因此相应的性能权函数的作用是调节系统跟踪性能，包括跟踪的快速性(上升时间)、跟踪的稳定性(超调量)、跟踪的准确性(稳态误差)等。根据设计经验，具体的选取方案与实际被控对象的特性有关，总围绕上述指标的期望值进行。一个共同的规则是：性能权函数的主要作用频段是中低频段，是一个中低通器，上升时间的快慢与性能权函数的截止频率有关，截止频率越高，上升时间就越快；超调量与高频段的幅值有关，幅值越大，超调量就越小；稳态误差与作用频段内的幅值有关，幅值越大，稳态误差就越小。

3.1.3 控制律设计指标

本文中控制律设计指标如下[7-8]。

a)时域指标：上升至80%稳态值时间tr≤0.5 s，超调量δ≤20%，稳态误差ess≤2%。

b)等效舵偏角绝对值不大于30°。

c)不确定性参数均能承受±1倍的拉偏。

d)要求基于某特征点设计的飞行控制系统能控制导弹在一定空域内沿弹道稳定、准确地飞行。

3.2 不确定性建模

3.2.1 未建模不确定

本文中，俯仰通道的未建模不确定性以输入端乘法不确定性的形式加入，如图6所示。则实际模型为

(13)

式中：Δ1为未建模不确定性的代数式；Win为规范化不确定性的权函数。为满足μ综合控制系统设计的先决条件，应合理选择Win，使‖Δ1‖∞<1。

3.2.2 参数不确定性

根据上述不确定性分析，以工作点2为标称模型，本文主要考虑Alon(1，2)，Alon(3，1)，Alon(3，2)，Blon(1)四个参数的不确定性。另考虑各主要不确定性参数能承受±1倍拉偏，考虑一定的裕量，参数不确定建模时按±1.6倍拉偏，折算到各参数为

(14)

(15)

其中不确定矩阵可利用奇异值分解得

BpCp

(16)

则加入参数不确定性的弹体模型可增广出两路关于参数不确定性Δ2(Δ2=diag[δδ])的输入输出

(17)

式中：z=[z1z2]T；w=[w1w2]T。

加入参数不确定性的俯仰通道增广模型结构如图7所示。

3.2.3 传感器测量噪声

本文中传感器测量噪声是以外输入扰动形式加入，如图8所示。俯仰通道飞行控制系统中，使用的传感器主要有加速度计与角速率陀螺。图8中：noise 1，noise 2分别为加速度计和角速率陀螺的测量噪声；Wn为权函数阵，用于调整传感器测量噪声的幅值。

3.3 控制结构设计

由控制律结构的设计，俯仰通道的稳定控制系统设计为加速度跟踪系统。另外，本文的控制结构及控制律设计中充分考虑未建模不确定性、参数不确定性、噪声干扰等。与这些干扰及不确定性相对应，控制结构及控制律设计中需设置相关的权函数，同时也要体现控制律的控制效用。权函数的设置如下。

a)设置用于限制控制信号幅值或外部扰动的权函数；

b)设置用于规范化未建模不确定性的权函数；

c)因本文的控制律设计是针对导弹的稳定控制系统，而稳定控制系统的作用是控制跟踪过载或姿态信号，故还需设置调节跟踪性能的权函数。

综合上述控制律结构、不确定性与权函数设置的方案设计，设计的控制结构如图9所示。由图9可知：这是一个加速度跟踪系统(相当于过载稳定控制系统)，未建模不确定性WinΔ1、参数不确定性Δ2及传感器噪声均已加入驾驶仪结构中。图9中：Control_lon为俯仰通道待设计的控制器；Actautor为舵机的传递函数环节；G_lon为已加参数不确定性的俯仰通道增广模型；Wideal为期望的理想响应环节，选取时可根据权函数设置中的设计指标，就能将对控制系统设计要求明确有针对性地体现在设计过程中；Wact为舵机限幅的权函数；Wn为调整传感器测量噪声幅值的权函数；Wp为调节控制系统跟踪性能的权函数，也称性能权函数。

根据前文对各不确定性分析及文献[9]中各权函数的设计法则，取

3.4 μ综合控制器设计

在Matlab环境中进行D-K迭代，最终设计出俯仰通道μ综合控制器[19]。迭代结果见表2。经过三轮D-K迭代，设计出一个19阶的控制器Control_lon，在参考频域范围内，俯仰通道闭环控制系统结

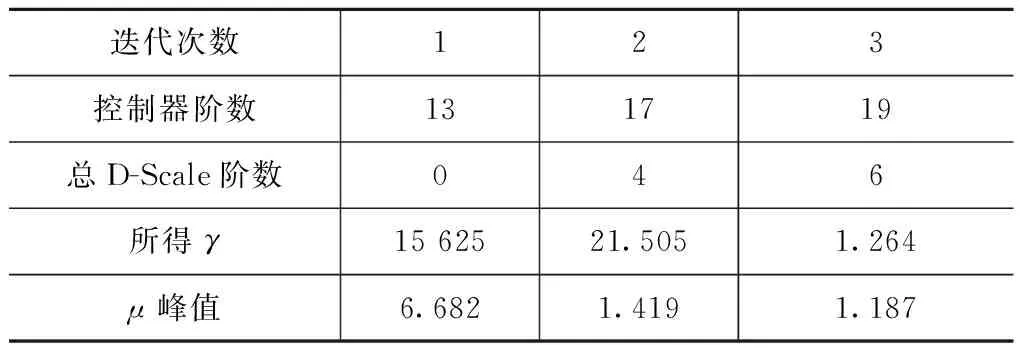
表2 俯仰通道μ综合控制器设计D-K迭代结果Tab.2 D-K iteration result of μ-synthesis controller for pitch channel

构奇异值μ值如图10所示。此时，最大结构奇异值μ值为1.187，表示该控制系统能承受的不确定性

(18)

4 仿真验证

4.1 μ分析

为评价摄动系统和控制器的性能，需检验标称性能、鲁棒性能和鲁棒稳定性能[20]。

4.1.1 标称性能

对标称对象工作点2，若在考查的频段范围内满足

(19)

则此俯仰通道控制系统满足标称性能。用MATLAB软件中的μ工具箱可计算并绘出标称性能μ值曲线如图10所示，参考频段为0.01～100 rad/s。由图10可知：在参考频段内

(20)

满足标称性能指标。

4.1.2 鲁棒稳定性能

对受扰系统，若在考查的频段范围内满足

(21)

则此俯仰通道控制系统满足鲁棒稳定性能。鲁棒稳定性能的μ值曲线如图11所示。由图11可知：在参考频段内

(22)

满足鲁棒稳定性能指标。另外根据鲁棒稳定性定理可知：在此频段内，在保证俯仰闭控制系统内部稳定情况下，该控制系统最大能承受的不确定性Δ满足

(23)

4.1.3 鲁棒性能

对受扰系统，若在考查的频段范围内满足

(24)

则此俯仰控制系统满足鲁棒性能。此处：T为俯仰闭控制系统全量传递函数阵。鲁棒性能的μ值曲线如图12、13所示。由图12、13可知：在参考频段内

(25)

说明控制系统并不满足鲁棒性能指标。根据鲁棒性能定理，这意味着，在保证俯仰闭控制系统内部稳定的条件下，该控制系统最大能承受的不确定性Δ满足

0.842 1

(26)

未能满足鲁棒性能的主要原因是对不确定性的评估过大，即在设计之初放大了控制系统对不确定性的容忍能力，这可通过缩小不确定性范围解决。另外，性能权函数的选取，D-K迭代的轮数等因素也会影响控制系统的鲁棒性，但若进行相应改进以优化鲁棒性能的代价是控制器的阶数会相应增大，甚至出现工程上不可实现的情况。虽然此鲁棒性能指标不能从定义上满足要求，但若能满足工程中的实际需求，此控制器及控制系统也是可取的。从工程实现角度考虑，本文认为只要鲁棒性指标μ值小于2，即认为满足要求。

4.2 时域仿真

单个标称工作点2的俯仰通道的阶跃响应分别如图14～16所示。其中：最坏不确定性扰动为Δ=diag[Δ1Δ2]满足式(18)。由图14～16可知：受扰响应和标称响应均能较好地跟踪理想响应曲线，表明在时域能满足控制律设计指标。另外假设稳定控制系统激励放大500倍(即给定50g过载激励)，俯仰角速率响应与出舵量响应均符合控制律设计指标。

工作点1、标称工作点2、工作点6、工作点7、工作点8、工作点12的俯仰通道阶跃响应分别如图17～19所示。由图17～19可知：本设计实现了一个控制器控制多个工作点的良好鲁棒性，且线加速度响应、俯仰角速率响应与出舵量响应均能满足提出的控制律设计指标。

值得注意的是，由俯仰通道鲁棒性指标maxμ(T)=1.187 5>1，可得该通道仿真能承受的最坏不确定性为‖Δ‖∞≈0.842 1。折算到参数不确定性，这意味着能承受的参数不确定性需在式(10)表示的摄动上(由1.6倍拉偏的折算得到)做0.842 1倍的折扣。折算后，每个摄动参数的拉偏能力为±1.189～±1.353倍，满足0.5倍拉偏的指标。

5 结束语

针对样例空空导弹，本文对其俯仰通道的稳定控制系统进行了μ综合控制律设计，考虑了未建模、参数、传感器噪声等不确定性的建模，设计了μ综合控制器。数字仿真结果表明：设计的稳定控制系统满足控制性能指标要求，有良好的鲁棒性与鲁棒稳定性；实现了一个控制器控制多个工作点，不但从根本上提高了飞行控制系统的鲁棒性，并且突破了经典控制系统中一个控制器控制少数几个工作点，需在飞行包络内进行复杂动态调参的传统控制模式。本文研究的导弹不确定性主要是未建模不确定性、气动参数不确定性和传感器噪声等。后续研究可完善导弹弹体的不确定性，如加入通道间耦合作用、风扰动、执行机构模型不确定性等不确定性因素，以强化设计的控制系统的鲁棒性。本文以工程应用为前提，参考国外文献，根据对象自身特性，所设计的控制结构较简单，权函数的设置也是基于现阶段的控制系统性能指标。随着后续对象和性能升级，需完善控制结构设计及权函数设置。

[1] 张肇蓉， 高贺， 张曦， 等. 国外制导空空导弹的研究现状及其关键技术[J]. 飞航导弹, 2016(3): 23-27+32.

[2] 月日新. 霹雳神箭——揭开中国“霹雳”导弹的面纱[J]. 海事大观, 2005(11): 31-38.

[3] 樊会涛, 刘代军. 红外近距格斗空-空导弹发展展望[J]. 红外与激光工程, 2005, 34(5): 564-568.

[4] BUSCHEK H. Design and flight test of a robust autopilot for the IRIS-T air-to-air missile[J]. Control Engineering Practice, 2003, 11: 551-558.

[5] LOMBAERTS T J J. Design of a robust flight control system for a mini-UAV[R]. AIAA, 2005-6408, 2005.

[6] 李作仁. 鲁棒自动驾驶仪设计述评[J]. 上海航天, 1995, 12(2): 48-53.

[7] 吴敏. 现代鲁棒控制[M]. 长沙: 中南大学出版社, 2006: 57-237.

[8] 史忠科. 鲁棒控制理论[M]. 北京: 国防工业出版社, 2003: 187-253.

[9] 刘慧. 一种新型空-空导弹的控制律研究[D]. 南京: 南京航空航天大学, 2010.

[10] BUSCHEK H. Full envelope missile autopilot design using gain scheduled robust control[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(1): 115-121.

[11] 钱杏芳. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2008: 155-258.

[12] 毕永建. 弹性体导弹鲁棒控制器设计[J]. 电光与控制, 2008, 15(4): 27-30.

[13] 刘林， 车军， 唐强， 等. 飞行控制律开发中的不确定性评估确认方法[J]. 系统仿真学报, 2007, 19(4): 840-878.

[14] 郑建华. 鲁棒控制理论在倾斜转弯导弹中的应用[M]. 北京: 国防工业出版社, 2001: 78-165.

[15] 李亮， 杨军. 巡航导弹姿态与过载自动驾驶仪对比研究[J]. 计算机仿真, 2009, 26(2): 77-83.

[16] DOYLE J C. Analysis of feedback systems with structured uncertainties[J]. IEEE Proceeding Part D, 1982, 129(6): 242-250.

[17] AMATO F. μ-synthesis for a small commercial aircraft: design and simulator validation[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(3): 479-489.

[18] BALAS G J, DOYLE J C, GLOVER K. μ-analysis and synthesis toolbox for use with MATLAB[M]. Natick: MUSYN Inc and the MathWorks, 2001: 2-230.

[19] BATES D G, KUREEMUN R. Improved clearance of a flight control law using μ-analysis techniques[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(6): 869-884.

[20] BELCASTRO C M, KHONG T H. Uncertainty modeling for robustness analysis of aircraft control upset prevention and recovery systems[R]. AIAA, 2005-6427, 2005.

Control System Study for New Air-to-Air Missile Based on μ-Synthesis Method

LIU Hui, ZHANG Jia-liang, SHAO Chang-xing, ZHANG Di

(Shanghai Electormechanical Engineering Institute, Shanghai 201109, China)

According to the problems of the non-linear model characteristic, coupling effect of each channel, uncertainty and unmodeled dynamics of the model of new generation air-to-air missile, the control technique of autopilot based on μ-synthesis method was studied, which could avoid too much conservativeness. The pitch channel was modeled for some air-to-air missile. The structure, determination of weight function, and design performance of control law were presented. The unmodeling uncertainty, parameter uncertainty and sensor noise were modeled. The control structure was designed. The μ controller was obtained by D-K iteration. The numerical simulation results showed that robust controller designed of pitch channel had met the requirement of control performance, which had good robust stability and robust performance and had good performance to suppress the effect of nonlinearity, coupling among channels, uncertainty and unmodeled dynamic characteristics. It realized that one controller could control multi-points, which break through the traditional control mode that one controller could only control some points and need to adjust parameters dynamically in the flying envelope curve.

air-to-air missile; μ-synthesis; robust; autopilot; uncertainty; pitch channel; control law; D-K iteration

1006-1630(2017)02-0134-10

2016-07-25；

2016-08-07

刘 慧(1986—)，女，硕士，主要从事战术导弹制导控制系统设计与研究。

TJ765.2

A

10.19328/j.cnki.1006-1630.2017.02.015