有大型挠性附件的卫星姿态线性鲁棒控制器设计研究

刘 刚,钟 超,何益康,胡恒建,钱方亮,钟金凤

(1.上海市空间智能控制技术重点实验室,上海201109; 2.上海航天控制技术研究所,上海201109)



有大型挠性附件的卫星姿态线性鲁棒控制器设计研究

刘 刚1， 2,钟 超1， 2,何益康1， 2,胡恒建1， 2,钱方亮1， 2,钟金凤1， 2

(1.上海市空间智能控制技术重点实验室,上海201109; 2.上海航天控制技术研究所,上海201109)

针对有大型挠性附件的卫星高精度高稳定度姿态控制问题，提出了一种基于H2/H∞混合控制理论的控制器设计方法。为尽量减少控制器变量的影响以提高其性能，选择刚体卫星模型建立了控制模型，卫星三轴姿态解耦，基于H∞方法分别设计了三轴控制器。引入三个输出量，考虑三者间关系，设计相应的加权系数，所得H∞控制器在数学仿真中有较佳的控制效果。考虑实际工程中源于控制周期和执行机构非线性的大幅值高频干扰等因素，用两种方法进行改进：一是设计H2/H∞混合控制，抑制噪声的影响，减小输出力矩的振荡；另一是在控制器的速率输入端添加滤波器，防止转速飞轮的高频干扰力矩激发控制器或整个系统的振动。设计的控制器以被动振动抑制方法为基础，考虑现有星上单机的技术条件及速率闭环飞轮的输出特性，通过选择合适的性能输出和反馈信息，在较低的闭环控制系统带宽下实现了大型挠性卫星的高精度高稳定度姿态控制。由数学仿真给出了设计的控制器及其性能，仿真和半物理试验结果均表明设计的H2/H∞混合控制器的控制精度、稳定度和挠性振动抑制效果均明显优于传统比例积分微分(PID)控制器。

大型挠性附件； 姿态控制；H2/H∞混合控制； 加权系数； 高频干扰； 鲁棒控制； 振动抑制； 半物理仿真试验

0 引言

有大型挠性附件的卫星具转动惯量大、受到的干扰力矩大、挠性振动频率低、对中心刚体的耦合作用强、模型不确定性对系统影响较大等特点，姿态控制难度远高于传统卫星。此外，针对此类卫星提出的空间观测任务，对指向精度和稳定度等的要求都较高。因此，需设计高精度高稳定度的姿态控制器以满足未来空间任务的需要。传统PID控制是当前卫星姿态控制采用的主要方法，目前已发射的卫星多采用PID控制或改进PID控制。PID控制器结构简单，可调参数较少，对系统控制模型要求较低，通用性强，可靠性高，可胜任卫星挠性附件较小或控制精度要求较低的任务。但由于PID控制器的控制精度与系统的带宽成正比，当挠性附件较大、振动模态频率较低时，为防止控制器激发挠性附件的振动，闭环系统的带宽只能在很低的频率范围内选取，导致整个系统的外干扰抑制能力变弱，从而无法得到较高的控制精度。因此，对大挠性卫星的高精度高稳定度控制，需基于任务要求和现有技术条件设计鲁棒性强的控制器。基于H∞理论的控制算法是一种应用广泛且效果理想的线性鲁棒控制方法。自20世纪90年代首次提出用H∞控制方法设计大型复杂卫星姿态控制器以来，国外对基于H∞等线性鲁棒控制在卫星上的应用进行了大量理论研究，并用于哈勃太空望远镜和日本ETS-8等大惯量大挠性卫星[1-9]。国内目前关于此类问题尚处于理论研究阶段，还未有真正的应用。文献[10-11]对基于输入成型的大型挠性卫星姿态控制进行了研究。本文在此基础上，在现有技术条件下，分析卫星建模和执行机构的不确定性对控制系统的影响，基于H∞理论研究了大挠性卫星的姿态控制，并用数学和半物理仿真对设计控制器的可实现性和有效性进行验证。

1 数学模型

设计控制器时，依据的数学模型对控制器的性能、可实现性，以及可靠性等有显著影响。现阶段对有大型挠性附件的卫星，工程中一般选择两种数学模型作为控制模型：考虑挠性附件的刚挠耦合动力学模型和传统刚体模型。选用刚体模型作为控制模型时，挠性振动等可建模的运动只能作为高频未建模动态进行处理；选用考虑挠性附件的模型时，模态的频率和阻尼等不确定性均可作为参数不确定性处理，降低最终所得控制器的保守性，利于控制器性能的提高。

由于H∞等线性鲁棒控制器可能自带状态变量，且控制器的状态变量数与被控系统的状态变量数成正比。因此，当控制模型中包含挠性附件时，最终得到的控制器阶数与需考虑的挠性模态数量有关。一般，单个挠性附件至少有2～3个挠性模态的影响较大，多个挠性附件需考虑的挠性模态则更多，导致最终设计的控制器阶数较高，能达十多阶甚至数十阶，不仅大幅增加了控制器的复杂程度和实现难度，而且过多的控制器变量也会降低整个系统的可靠性。此外，受目前技术条件限制，星上的大部分模态挠性无法测量，即模态信息无法作为控制器的输入量。控制器设计时采用不激发挠性振动的被动抑制策略，故控制模型中考虑挠性振动主要是减小控制器设计的保守性，难以显著提高控制器的性能。因此，与刚挠耦合动力学模型相比，采用刚体动力学虽会增加设计的保守程度，牺牲部分控制器性能，但可明显降低控制器的阶数。为尽量减少人为添加的控制器变量的影响，提高控制器的可靠性，本文选择刚体卫星模型作为控制模型进行设计。

用误差四元数描述的卫星姿态运动学和动力学模型分别可表示为

(1)

(2)

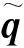
(3)

式中：qbo，qco分别为卫星本体系和参考姿态四元数的矢部。则ωe可表示为

(4)

式中：ω为卫星角速度。

因H∞控制器是针对线性系统设计的，故需对上述误差四元数数学模型在参考姿态附近进行线性化，得最终用于控制器设计的模型为

(5)

(6)

式中：uc为H∞控制器的输出量，包括抵消动力学模型中非线性项作用的补偿项。

在上述控制模型的建立中，卫星三轴姿态实现了解耦，因此可对三个轴分别进行控制器设计。为提高系统对外界干扰力矩的抑制能力，本文选择卫星的误差姿态角(四元数)和误差角速度作为控制器的输入量，控制器输出量为控制力矩，即单轴的控制器为一个双入单出的系统。虽然此时控制器与传统的全状态反馈静态控制器的输入变量相同，但由于需考虑整个系统包含加权函数的状态变量，其本质仍是输出反馈控制器。

2 控制器设计

针对大挠性卫星自身结构的特点，以及控制模型为刚体模型的限制，为在实现高精度高稳定度控制的同时不激发挠性附件自身的振动，需控制器能在较低的闭环带宽下取得较好的不确定性以及外干扰抑制能力。控制器需满足两个基本要求：闭环系统的带宽足够低，不会激发挠性附件等未建模结构的振动；系统对外界干扰及自身的模型不确定性具良好的抑制能力，在满足稳定性条件的同时，能保证控制精度等性能满足任务要求。

传统PID控制器时很难同时实现上述要求，但在设计H∞控制器时，可通过选择合适的性能输出量及加权函数，构成混合灵敏度问题求解实现。本文选择如图1所示的H∞控制系统的性能输出量进行控制器设计。

图1中：y为控制器的输入量，即单轴误差姿态角和误差角速度；u为控制器的输出量，即控制力矩；G0(s)为名义系统(即不考虑不确定性的理想卫星模型)的传递函数；Δ(s)为归一化后的乘性不确定性，满足Δ(s)<1。三个性能(被调)输出为z1，z2，z3，其中：z1可反映系统的控制精度以及抗干扰能力，即系统在低频段的性能；z3可反映系统对模型不确定性的鲁棒性，即对高频不确定性(如挠性模态、控制器采样、执行机构输出特性等未建模因素)的抑制能力；z2可起到控制输出增益限幅的作用，防止控制器输出的控制力矩过大。针对这三个性能输出，可得用H∞范数描述的混合灵敏度问题

(7)

式中：S为系统灵敏度，即不确定性影响w至z1的传递函数；R为w至z2的传递函数；T为系统闭环传递函数；W1(s)～W3(s)为性能输出的加权函数；γ为不大于1的正数，为保证系统的鲁棒性和减少控制器的保守性，可取γ=1。

通常，为抑制干扰对控制精度的影响，需尽可能降低S在低频段的增益；为保证控制器输出的力矩符合实际执行机构的要求，需对R进行幅值限制；为抑制高频模型不确定性的影响并限制系统带宽，也需在满足鲁棒性要求的情况下尽可能压低T的高频增益及转折频率。通过引入输出量z1，z2，z3，控制性能的要求可直接体现在H∞控制器设计中，随后只需设计加权函数W1(s)～W3(s)，即可得符合第三个要求的控制器。

3 加权函数设计

由上述分析可知：加权函数直接决定了控制器的性能，故控制器设计的重点是加权函数。在设计加权函数时，需综合考虑系统的三个性能输出量间的关系，以及最终得到的系统所需的控制器是否存在，即控制器是否可解。整个过程是一个反复“设计-试验-再设计”的过程。

输出量z1反映系统的控制精度及抗干扰能力，设计W1(s)时需使S的频域响应曲线在低频段幅值较低，转折频率尽可能高，同时保证最终控制器可解。

输出量z2反映控制器输出力矩的大小，本文只需选取一固定值，即保证R为有限增益且控制器可解即可。

输出量z3不仅反映系统对系统模型不确定性的抑制能力，而且直接反映系统的带宽，因此W3(s)需尽可能覆盖不确定性的频域响应曲线，同时不能过于保守而导致系统带宽无法降低。本文用乘法不确定性描述系统的不确定性，考虑的不确定性包括卫星质量、挠性振动和执行机构的动态(采用一阶惯性环节近似)。设名义模型传递函数为G0(s)，则实际模型的传递函数

(8)

式中：

(9)

设计得到的W3(s)需覆盖不确定性，即满足

(10)

此外，W3(s)也应保证控制器可解。

加权函数确定后，即得能用于控制器计算的增广系统的状态空间表达式为

(11)

式中：x为增广系统的状态量(包括姿态角、角速度以及加权函数引入的状态量)；z为性能输出量；y为反馈至控制器的系统输出量；w为干扰输入；u为控制量；A，B1，B2，C1，C2，D11，D12，D21，D22为根据增广系统传递函数计算得到的状态空间矩阵。得到增广系统后，用Matlab的鲁棒控制工具箱可求得所需的控制器。对求得的控制器进行离散化处理，即可得适于星载软件的滚动轴离散H∞控制器。

4 飞轮高频干扰力矩的影响及H2/H∞混合控制

上述求得的H∞控制器在连续系统数学仿真中可有非常好的控制效果。但受当前的技术条件所限，实际应用中由于执行机构的非线性特性、控制采样周期，以及测量噪声等因素的影响，H∞控制器往往不能取得令人满意的效果。这些影响因素中，控制周期和执行机构的非线性对系统影响较大，特别是工作在转速控制模式的反作用飞轮(以下简称为转速飞轮)，会引入大幅值的高频干扰力矩，对控制效果和稳定性的影响非常严重。

目前姿态控制使用的多数反作用飞轮在转速(动量)控制模式下工作。转速飞轮并不直接输出给定的指令定力矩信号，而是通过跟踪给定的角动量间接输出控制力矩。当指令力矩为方波信号时，转速飞轮响应如图2所示。其中采样周期为0.5 s。

由图2可知：当飞轮工作于转速模式时，其响应力矩类似于脉冲的形式，且峰值远大于输入的指令力矩，可近似视为在原来给定力矩的基础上叠加了一个大脉冲干扰力矩。通过截取控制过程中某时间段的控制器指令力矩和转速飞轮实际输出力矩，并对其进行小波变换，得到各信号的时频谱，从中可发现这些叠加的脉冲力矩包含的信号频率。系统在稳态下50 s内的指令力矩和转速飞轮输出力矩及其经小波变换后的时频图如图3～6所示。

小波变换中，尺度与频率成反比，尺度值越大，对应的频率越低。由图6可知：转速飞轮输出力矩在低频段(大尺度区)与指令力矩类似，但高频段(小尺度区)的幅值并未衰减，反明显超过低频段的峰值(图6中椭圆区域)。这些大幅值的高频干扰力矩会对整个系统的稳定性造成严重的不良影响。当使用PID控制器时，该特性会限制微分项的取值，降低系统的抗干扰能力。对所设计的H∞控制器，转速飞轮引入的高频干扰力矩很可能导致系统振荡或发散。

造成上述情况的原因，是因为在加权函数设计中转速飞轮的特性难以描述，当控制周期较大时，加权函数无法保证能覆盖飞轮引入的不确定性。即使能在频域分析时近似考虑转速飞轮的这种不确定性，但由于该不确定性的增益覆盖范围较广，得到的H∞控制器将非常保守，性能远不能满足当前任务的要求。因此，在使用转速飞轮时，H∞控制器难以完成任务。为解决该问题，本文用以下两种方法对控制器进行改进：

a)改进控制器，抑制测量噪声对控制器输出力矩的影响，减少输出力矩的振荡；

b)在控制器的速率输入端添加滤波器，防止转速飞轮的高频干扰力矩激发控制器或整个系统的振动。

对第一种方法，可通过加入H2性能指标，设计H2/H∞混合控制实现。因H2范数的平方等于系统脉冲响应总的输出能量，故可一定程度减弱测量噪声、较长的控制周期，以及飞轮非线性特性对整个系统的影响。

为防止飞轮引入的高频干扰力矩导致控制器输出量包含不需要的高频信号进而激发系统挠性振动，需选择干扰力矩作为输入，控制器的输出作为H2性能指标的输出量。此时从输入至输出的传递函数与选择测量噪声为输入，系统姿态角为输出时的传递函数相同，为不增加w的维数，本文选择后两者作为控制器设计时的输入输出量。此时被控系统的状态空间表达式变为

(12)

式中：z∞为H∞性能输出量；z2为H2性能输出量；C1∞，D11∞，D12∞，C12，D112，D122为增广系统的输出矩阵，可通过将输入至性能输出的传递函数转换至状态空间得到。

加入H2性能指标可一定程度降低飞轮输出力矩中的高频干扰力矩。但当控制采样周期较大时，飞轮输出力矩中的脉冲干扰力矩包含的信号频谱更广，加入H2性能指标并不能完全解决高频干扰力矩的影响。这时需采用上述第二种改进方法，在控制器的速率输入端添加滤波器。因空间中的干扰力矩频率较低，与飞轮高频干扰力矩的频率间隔较远，故为简化控制器的计算，可采用最简单的一种处理方法，添加低通滤波器滤除高频干扰力矩的影响。

在相同控制器设计参数条件下，设低通滤波器时间常数50 s，H∞控制器、H2/H∞混合控制器和H2/H∞混合控制器+低通滤波器的开环幅频曲线仿真结果如图7所示。由图7可知：在低频段，H2/H∞混合控制器的增益较H∞控制器并无衰减，甚至更大，利于对低频干扰力矩的抑制；在中频段，H2/H∞混合控制器的增益有所降低，对测量噪声起到了一定的抑制效果；在高频段，虽然H2/H∞混合控制器的增益较H∞控制器有一定的降低，但幅值仍较大，存在引起系统振动的风险。添加低通滤波器后，H2/H∞混合控制器在高频段的增益被限制在较低的范围内，可屏蔽飞轮高频干扰力矩对控制器的影响，防止激发系统振动。

5 数学仿真

5.1 输入条件

在Simulink环境中对H2/H∞混合控制器进行纯数学仿真以验证H2/H∞混合控制器的有效性，选取带有两个大型挠性附件的卫星作为被控对象。仿真输入条件如下。

仿真模型：刚挠耦合的卫星动力学模型；挠性附件展开后整星的真实转动惯量

控制器计算使用的转动惯量

挠性附件1(两个，星体左右对称安装)的频率0.125，0.418，0.430，0.722，1.400，2.112，2.729 Hz；挠性附件2(两个，星体前后对称安装)的频率0.300，0.438，1.000，1.631，1.999，3.099，3.655，3.919，4.246，4.787，4.808，5.632，5.984 Hz；挠性附件阻尼比0.005；挠性模态频率拉偏，缩小为1/3；反作用飞轮，最大角动量25 N·m·s，最大输出力矩0.2 N·m；星敏感器测量精度优于8″；光纤陀螺测量精度优于0.000 5 (°)/s；控制周期0.5 s；姿态采样延时40 ms；外干扰力矩包括重力梯度力矩、太阳光压力矩、剩磁干扰力矩和气动力矩；控制器补偿力矩仅包括动力学中的非线性项；初始姿态偏差，三轴均为0.15°。

5.2 控制器设计结果

根据上述输入条件，选取加权函数

(13)

W1(s)，W3(s)的幅频特性如图8所示。

由图8可知：W1(s)在低频段幅值较大，中频段幅值下降较缓慢，高频段则幅值较低，对应的系统灵敏度S将具有相反的特性，即低频段幅值较低，保证理想情况下系统的控制精度，较宽的中频段可使系统对分布在一定范围内的低频外干扰有较好的抑制效果，高频段受物理特性所限，将稳定在0 dB。W3(s)在0.01 rad/s后快速升高，限制了系统带宽，防止控制器激发挠性附件的振动。

考察W3(s)对不确定性的覆盖性。以滚动轴为例，G0(s)W3(s)、考虑挠性模型且转动惯量拉偏正负20%以及无拉偏的G(s)-G0(s)的奇异值曲线如图9所示。

此处需说明的是：W3(s)选取时考虑的仅是系统中可用线性模型表示的不确定性，实际系统中还有许多不确定性难以用线性模型描述，无法在Bode图中表现，因此虽然W3(s)的幅频曲线满足了性能要求，但实际上很可能存在没有覆盖的不确定性，故实际应用时还需对控制器参数进行调整。

用Matlab软件中的相关函数，并进行控制器降阶后，即可求得所需的H2/H∞混合控制器。三轴的控制器传递函数矩阵分别如下。

a)滚动轴

(14)

式中：

b)俯仰轴

(15)

式中：

c)偏航轴

(16)

式中：

求得控制器后，考察闭环系统的灵敏度传递函数和输入输出闭环传递函数与加权函数的幅频曲线，结果分别如图10、11所示。由图10、11可知：该控制器能使系统的闭环特性满足预期的性能。

分析本文设计的控制器的稳定性，加入控制器后开环系统的Bode图得到系统的稳定裕度信息。用H2/H∞混合控制器时卫星滚动轴的开环Bode图如图12所示。由图12可知：系统开环截止频率小于0.01 rad/s，相角裕度71.7°，幅值裕度21.6 dB，说明H2/H∞混合控制器带宽较低，且具较好的稳定裕度。

5.3H∞/H2混合控制数学仿真结果

仿真所得三轴姿态角及其角速度分别如图13～16所示，三轴控制力矩和模态位移分别如图17、18所示。由图13～18仿真结果可知：H2/H∞混合控制器控制输出的指令力矩更平滑，对挠性振动的抑制效果较好，控制精度和稳定度非常高，优于0.000 5°，远高于目前星上使用的PID控制器。

6 半物理仿真

半物理试验中所用姿控设备均为目前星上能使用的单机和传感器，系统连接如图19所示。其中：光纤陀螺安装在三轴转台上，可获得真实的转动速率。

a)大初始姿态偏差时H2/H∞混合控制

设卫星三轴都存在较大的初始姿态误差，分别为滚动轴(6°，0.03 (°)/s)、俯仰轴(1°，-0.001 (°)/s)、偏航轴(2°，0.000 5 (°)/s)，用H2/H∞混合控制所得姿态角、姿态角速度和控制力矩结果分别如图20～22所示。

从上述仿真结果可知：无需加入递阶饱和等改进策略，H2/H∞混合控制器就能实现大初始姿态偏差下大挠性卫星的姿态调节控制，且整个过程中挠性附件的振动保持在较小的范围内。收敛过程既表现出了一定的欠阻尼特性(动态过程的前半段)，收敛速度较快，也表现出了过阻尼的特性(动态过程的后半段)，超调量较小。在仿真中，由于飞轮角动量的限制，俯仰轴和偏航轴的初始角速度的取值较保守，如能增加飞轮的最大角动量，H2/H∞混合控制器可实现更大初始角速度下的姿态稳定控制。

b)H2/H∞混合控制与PID控制比较

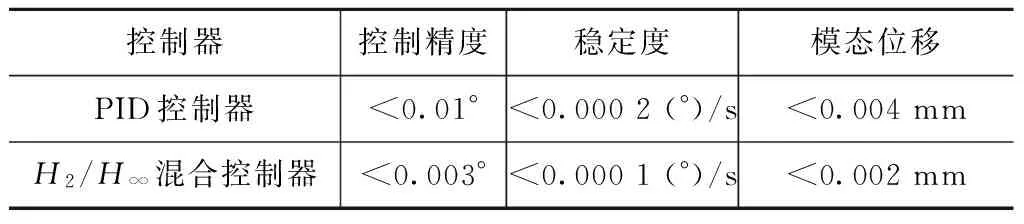
对稳定控制中传统PID控制器和H2/H∞混合控制器的控制效果进行比较，以进一步验证本文设计控制算法的优势。其中：所用PID算法为目前已在轨运行的卫星应用的双环(串级)PID控制算法。为突出试验效果，所有模态频率均缩小至1/3。试验结果如图23～25所示。半物理试验所得结果见表1。

控制器控制精度稳定度模态位移PID控制器<0.01°<0.0002(°)/s<0.004mmH2/H∞混合控制器<0.003°<0.0001(°)/s<0.002mm

由半物理仿真结果可知：H2/H∞混合控制器的控制精度、稳定度及挠性振动抑制效果均明显优于传统的PID控制器。虽然仿真中动力学模型所用的挠性模态振动频率与设计值相比缩小了2/3，但由于H2/H∞混合控制器的带宽较低，所激发的挠性振动位移仍很小，表明该控制算法对挠性振动有较好的抑制作用。

由上述试验结果可认为，根据简化动力学模型设计的H2/H∞混合控制器能实现高精度高稳定度的卫星姿态控制，并在控制过程中将挠性附件的振动模态抑制在较小的范围内。虽然H2/H∞混合控制器的可靠性略逊于PID控制器，但对挠性振动的被动抑制效果较好，控制精度和稳定度更高，如能改善控制周期、飞轮输出特性等技术条件，H2/H∞混合控制器还可获得更好的控制效果，在未来的大挠性卫星高精度高稳定姿态控制中有较大的应用潜力和价值。

7 结束语

本文基于H∞和H2控制理论设计了有大型挠性附件卫星的高精度高稳定度控制器。考虑现有的技术条件限制，以被动挠性振动抑制策略为基础，在不提高控制器带宽的前提下，提高卫星对模型不确定性和外部干扰力矩的抑制能力，实现高精度高稳定度控制。本文对设计的控制器进行了数学和半物理仿真，结果表明：在现有技术条件下，根据简化动力学模型设计的H2/H∞混合控制器可用于大挠性卫星的姿态高精度高稳定度控制。与传统PID控制器相比，H2/H∞混合控制器所需的带宽更低，控制精度更高，受转动惯量等不确定性的影响更小，对挠性振动的被动抑制效果更强，有非常大的应用潜力和价值。但本文仅针对速率闭环控制的飞轮特性进行了分析，而实际中姿控系统的执行机构还包括喷气系统、控制力矩陀螺和电推进器等。后续将进一步研究这些执行机构对控制器设计和挠性振动耦合的影响。

[1] SAFONOV M G, CHIANG R Y, FLASHNER H.H(infinity) robust control synthesis for a large space structure[J]. Journal of Guidance, Control, and Dynamics, 1991, 14(3): 513-520.

[2] MCFARLANE D, GLOVER K. A loop-shaping design procedure usingH∞synthesis[J]. IEEE Transactions on Automatic Control, 1992, 37(6): 759-769.

[3] LE BALLOIS S, DUC G.H-infinity control of an Earth observation satellite[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(3): 628-635.

[4] CHIANG R. Integrated robust control design methodology for an advanced S/C with large flexible structure[C]// Proc of AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu: AIAA, 2008: 2008-701.

[5] BONG W, LIU Q, BAUER F. Classical and robustH, control redesign for the Hubble Space Telescope[J]. Journal of Guidance, Control, and Dynamic, 1993: 16(3): 427-430.

[6] BUKLEY A P. Hubble Space Telescope pointing control system design improvement study results[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(2): 194-199.

[7] OHTANI T, HAMADA Y, NAGASHIO T, et al. Robust attitude control using mu-synthesis for the large flexible satellite ETS-Ⅷ[J]. The Journal of Space Technology and Science, 2009, 25(1): 27-40.

[8] HAMADA Y, OHTANI T, KIDA T, et al. Synthesis of a linearly interpolated gain scheduling controller for large flexible spacecraft ETS-Ⅷ[J]. Control Engineering Practice, 2011, 19(6): 611-625.

[9] NAGASHIO T, KIDA T, HAMADA Y, et al. Robust two-degrees-of-freedom attitude controller design and flight test result for Engineering Test Satellite-ⅧSpacecraft[J]. IEEE Transactions on Control Systems Technology, 2014, 22(1): 157-168.

[10] 胡恒建, 李英波, 施桂国. 空间站帆板驱动输入成型鲁棒控制[J]. 上海航天, 2016, 33(1): 13-18.

[11] 刘德庆, 彭仁军, 张子龙. 基于路径规划和输入成型的挠性航天器振动控制方法[J]. 上海航天, 2014, 31(4): 41-47.

Linear Robust Control Design Methodology for Satellite with Large Flexible Structure

LIU Gang1, 2, ZHONG Chao1, 2, HE Yi-kang1, 2, HU Heng-jian1, 2,QIAN Fang-liang1, 2, ZHONG Jin-feng1, 2

(1. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;2. Shanghai Institute of Spacecraft Control Technology, Shanghai 201109, China)

A linear robust control designH2/H∞control based onH2/H∞control was put forward for the high precision attitude control system of spacecraft with large flexible structures in this paper. To reduce the effect of controller’s variables and improve the performance of the controller, the ridge body was selected to establish the control model. The satellite attitudes of three axes were decoupled. The controllers of three axes were designed based onH∞method. The three outputs were introduced. The relative weight coefficients were designed with the consideration of the relationship among the three coefficients. The controllerH∞designed had good performance in the numerical simulation. But considering the high frequency disturbance with large amplitude caused by control period and nonlinear actuator in engineering, the controller designed was improved by two ways. One was to designH2/H∞controller to suppress the noise effect and reduce the oscillation of output moment. The other was to add filter to the velocity input end of the controller for avoiding exciting vibration of the controller or the whole system caused by high frequency disturbance moment of rotating flywheel. Based on the passive vibration suppression method, the high-precision controller with low closed-loop bandwidth was obtained through using the linear robust control theory under the consideration of the present onboard states and the output feature of rotation closed-loop flywheel. The controller design and its performance were given by numerical simulation. The results of the numerical simulation and hardware-in-the-loop simulation showed that the performances of theH2/H∞controller designed, such as control accuracy, stability and flexible vibration suppress, were better than traditional PID controller.

large flexible structure; attitude control;H2/H∞control; weight coefficient; high frequency disturbance; robust control; vibration suppression; hardware-in-the-loop simulation

1006-1630(2017)02-0150-11

2016-05-09；

2016-06-08

刘 刚(1985—)，男，博士，主要研究方向为大型复杂航天器的高精度高稳定度姿态控制。

V448.22

A

10.19328/j.cnki.1006-1630.2017.02.017