基于GPS测量数据的卫星在轨轨道预报算法研究
2017-04-28孙华苗李立涛张迎春
刘 燎,孙华苗,李立涛,张迎春,
(1.深圳航天东方红海特卫星有限公司,广东 深圳 518064; 2.哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001)
基于GPS测量数据的卫星在轨轨道预报算法研究
刘 燎1,孙华苗1,李立涛2,张迎春1, 2
(1.深圳航天东方红海特卫星有限公司,广东 深圳 518064; 2.哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001)
为提高微小卫星的在轨轨道预报能力,针对常用的低轨近圆卫星轨道,根据解析的轨道动力学模型,基于无奇点变量的拟平均要素法,用Kalman滤波技术给出了一种卫星解析星历参数在轨估计算法,用GPS测量信息对相关星历模型参数进行在轨估计。给出了算法流程。先由外部标志判断滤波器初始化状态,若需初始化,则可基于GPS测量数据,或地面上注星历参数,或上次滤波所得星历参数进行;若初始化已完成,则对星历模型参数进行Kalman滤波,得到更新的星历参数。给出了滤波算法中轨道预报、残差计算、量测计算和UD分解的计算模型。仿真结果表明:对轨道高度450 km以上的近地圆轨道,7 d内的预报精度优于20 km。算法具自启动(自初始化)、收敛性佳、对测量数据的采样要求不严格等优点,实用性好。
微小卫星; 自主能力; 低轨近圆卫星轨道; 星历模型; 轨道预报; GPS测量数据; 拟平均要素; Kalman滤波
0 引言
随着目前国内外卫星技术的不断发展尤其是卫星组网的发展,对卫星在轨自主能力的需求不断增加,在轨实时轨道确定成为判断卫星是否具有自主能力的首要条件。随着低成本全球导航系统接收机(包括美国的GPS及中国的北斗导航系统)的应用,在微小卫星上进行实时轨道确定进而提高小卫星的自主能力,已成为目前的一种发展趋势[1-2]。
卫星星历的计算有解析法、数值法和半解析法等三类,受星载计算机计算能力的制约,我国星上轨道预报目前都采用仅考虑地球非引力场主要带谐项和大气摄动主要长期项的拟平均要素法[3-4]。目前基于GPS测量信息的卫星实时在轨轨道确定主要采用Kalman滤波及基于轨道动力学模型的轨道确定技术,对卫星的瞬时轨道状态(位置和速度矢量)或密切轨道要素进行估计,以实时提供卫星的高精度轨道确定信息。其结果主要用于卫星各种实时应用,如图像的地理定位编码、敏感器与可驱动天线的指向,以及卫星三轴姿态控制[5]。但采用这种轨道确定技术的导航系统,很难用于长期的在轨星历预报(如数个轨道周期后甚至数天后的轨道预报),而这恰是卫星自主任务规划和自主管理所需的。其主要原因是:基于瞬时轨道参数或密切轨道要素进行轨道预报,需进行复杂的、计算量较大的轨道动力学数值积分运算,常需占用大量的星载计算机机时,因而不适于进行长期轨道预报[6]。文献[7]提出了一种采用简化的动力学模型和一种嵌套插值算法的积分器进行高精度的卫星星历计算,可实现轨道预报1 d精度优于1 km的星历计算,但也需要高性能的星载机,不适于微小卫星的轨道预报应用。
针对目前常用的低轨近圆卫星轨道,本文基于解析的轨道动力学模型,采用Kalman滤波技术,给出了一种卫星解析星历参数在轨估计算法,利用GPS测量信息对相关星历模型参数进行在轨估计[8]。可对任意时间间隔的卫星星历进行预报,而不用按步长对轨道进行积分,其计算量相对较小,对星载机的性能要求不高,可满足微小卫星的使用要求,能对卫星进行中期或长期的轨道预报(多个轨道周期或1周以上)。本文对基于GPS测量数据的卫星在轨轨道预报算法进行研究。算法具有自启动(自初始化)、收敛性好、对测量数据的采样要求不严格(允许测量数据以非均匀间隔时间给出,采样时间可在数秒至十多分钟内变化)的优点,甚至允许在轨道的某段时间内无测量数据情况下(如GPS天线被地球遮挡或接收机出现临时性故障),滤波器仍能正常运行。根据定义不同,平均要素又可分为平均要素和拟平均要素,其中平均要素只包含了长期变化项,拟平均要素包含长期变化项和长周期变化项,长周期变化项的周期能达到数月,因而在轨道问题研究中其影响不可忽略,同时拟平均要素能消除通约奇点问题,因而本算法采用基于无奇点变量的拟平均要素法[9]。为简化星上计算量,计算过程仅考虑了一阶精度。
1 星历参数选择
近地卫星主要受地球引力、大气阻力、太阳光压以及日月引力等作用,轨道变化包括长期变化项、长周期变化项和短周期变化项。长期变化即轨道参数随时间的线性或二阶及更高阶的变化;长周期变化主要由地球引力场带谐调和项引起;短周期项一类是由地球扁率引起的,另一类是由地球引力场的田谐调和项引起的。田谐项的摄动非常复杂,对小偏心率的轨道只需取其低频部分便可获得很高的精度,但在星上计算田谐项系数则需占据相当一部分内存和计算时间[10]。为简化计算,在模型中仅考虑长期和长周期变化项。
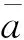
2 算法及计算流程
本文算法采用基于无奇点变量的拟平均要素法,使用Kalman滤波技术,利用GPS测量信息对相关星历模型参数进行在轨估计。为减少滤波过程中计算误差和舍入误差对滤波器状态误差协方差矩阵正定性的影响,避免长时间计算过程滤波器发散,采用Bierman-UD分解形式的Kalman滤波技术。算法的流程如图1所示。
本文算法的具体过程如下。
a)根据外部给出的是否进行滤波器初始化的标志判断当前计算状态。
b)若此时需进行初始化,则根据初始化方法标志分别进行滤波器初始化。此处:初始化方法有三种:一是根据GPS测量数据进行滤波器初始化,即由GPS提供的测量数据,计算所需测量时刻对应的轨道平要素集的初始猜测;二是根据地面上注的星历模型参数进行初始化;三是用上次滤波器计算收敛获得的星历参数进行初始化。后两种初始化方法基本相同。初始化完成后,将初始化标志置位。
c)若本次计算过程中初始化已完成,则进行Kalman滤波计算,对星历模型参数进行滤波,得到更新的星历参数。
3 基于GPS测量数据的初始化
利用GPS测量数据对历元时刻轨道平要素滤波器进行初始化。即根据GPS提出的测量数据,计算所需测量时刻对应的轨道平要素集的初始猜值,该初始化过程如下。
a)将GPS测得的位置与速度矢量转换至TOD系中;
b)将TOD坐标系中的位置与速度矢量转换为瞬时轨道要素;
c)通过迭代计算平均轨道要素,并给出对应星历模型参数;
d)根据提供的参数计算状态误差协方差矩阵,并进行UD分解;
e)输出时刻tGPS对应的星历模型参数以及初始U0,D0阵。
4 利用地面上注数据或上次滤波结果的初始化
本文算法是用地面上注的或前次Kalman滤波器给出的星历模型参数,对本次滤波过程进行初始化,该初始化过程如下。

b)根据提供的参数计算状态误差协方差矩阵,并进行UD分解;
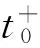
5 星历模型参数滤波过程算法
本文算法是利用基于Bierman UD分解Kalman滤波公式对星历模型参数进行滤波,得到更新的星历参数以及协方差矩阵对应的U,D阵,滤波算法的主要计算步骤如下。
a)根据上一步滤波得到的星历模型参数X以及其对应的历元时刻t0,进行轨道预报,得当前GPS测量数据时刻tGPS对应的卫星位置矢量(TOD系中)。
b)计算残差;若残差大于给定的容限,则判断为野值,退出当前滤波过程;否则执行步骤c)。
c)用有限差分法计算滤波所需的量测矩阵。
d)进行UD分解滤波,获得更新星历模型参数X+和协方差阵对应的U+,D+。
5.1 轨道预报算法
对时刻t0的星历模型参数进行轨道外推,以获得时刻t1的瞬时轨道位置和速度矢量(TOD系中),计算过程如下。
a)根据历元时刻t0及对应的星历参数,计算获得时刻t1的平均轨道参数
b)计算纬度幅角的平均值
c)计算时刻t1各轨道要素的短周期项
d)计算时刻t1的瞬时轨道要素
u=λ+2esinM+1.25e2sin(2M)
式中:X=a,i,Ω,ξ,η,λ。
e)计算时刻t1对应的位置与速度矢量
R=r(Pcosf+Qsinf)
5.2 残差计算
根据时刻tGPS的GPS测量数据RGPS和进行轨道预报得到的时刻tGPS卫星位置矢量R计算残差,计算步骤如下。
a)计算时刻tGPS的格林威治恒星时角S及坐标转换矩阵Rz(S)
S=mod(S,2π)
b)计算残差
5.3 量测矩阵计算
用有限差分方法计算卫星位置矢量预报值(TOD系)与星历参数的偏导数矩阵,进而求得量测矩阵,计算步骤如下。
a)令i=1。
b)生成第i个元素带扰动量的星历参数向量
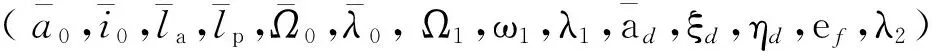
d)计算卫星位置矢量预报值与第i个星历参数的偏导数矩阵
e)若i=14,则转步骤f),否则i=i+1,转步骤b)。
f)计算量测噪声矩阵H
5.4 UD分解滤波算法
本算法主要是对上一步滤波过程得到的协方差U阵和D阵以及滤波状态进行更新,计算步骤如下。
a)令l=1,按以下步骤对第l个测量进行滤波更新。
b)计算变量αl和向量f,v,有
d)对滤波状态量和协方差阵进行更新
e)若l大于等3,则计算结束;否则令l=l+1,转步骤b)。
d)输出Xk/k,Uk/k,Dk/k。
6 仿真验证
为对本文提出的算法进行误差分析,需有参考的精确卫星运行轨道。用卫星工具箱STK中的生成基准轨道,设仿真参数为:轨道积分HPOP;引力模型JGM-3;太阳光压Cr=1.0,面质比0.02 m2/kg,阴影区模型Dual Cone;气动阻力Cd=2.2,面质比0.02 m2/kg,大气密度模型Jachia-Roberts;转动惯量Ixx=4 500 kg·m2,Iyy=4 500 kg·m2,Izz=4 500 kg·m2;三体引力为太阳、地球、卫星。输出的WGS84坐标系中卫星信息作为GPS测量数据,取采样间隔分别为1,5 min,滤波时间5 d,对卫星的轨道进行预报,预报时间1~7 d,与生成的TOD系中轨道数据对比。所得轨道高度450,600,700,800 km的预报精度分别如图2~9所示。
由图2~9可知:对轨道高度500 km以上的近地近圆轨道,本文算法的拟合精度优于约1.5 km,在不同采样间隔、不同轨道高度情况下,滤波2.5 d,预报1~7 d的轨道精度均优于20 km,可用于卫星光照/阴影区计算、地面站通信时机预报或地面成像目标规划等任务,其时间精度优于3 s。
基于传统14平轨道要素进行的轨道递推仿真结果如图10所示。由图10可知:累积误差较大,需定时由地面进行参数上注,不适于未来卫星自主任务管理发展的要求。
7 结束语
针对卫星长期自主运行需求,本文研究了基于GPS测量数据的卫星自主轨道预报方法。本文方法基于解析的轨道动力学模型,采用Kalman滤波技术,给出了一种卫星解析星历参数在轨估计算法,轨道预报精度较前人方法有显著提高;用基于Bierman UD分解的形式,可有效避免长时间计算引起的滤波器发散,自适应性好,对数据采样要求不高,具较好的鲁棒性,对微小卫星有较好的实用性,计算量少,降低了星载机的计算量,尤其适于低成本微小卫星的自主任务管理,可对卫星进行中期或长期的轨道预报(多个轨道周期或1周以上)。用数学仿真对本文方法的有效性进行了验证。研究发现:本文算法采用基于无奇点变量的拟平均要素法,具有自启动(自初始化)、收敛性好,且显著减少了星上计算量,以及对测量数据的采样要求不严(允许测量数据以非均匀间隔时间给出,采样时间可在数秒至十多分钟内变化)的优点;对轨道高度450 km以上的近地近圆轨道,在滤波2.5 d的条件下,预报精度优于20 km,轨道坐标系变换导致的误差约0.012°,可用于中等精度的姿态确定。本文方法的缺点是仅适于近地圆轨道的轨道预报。此外,在建模中未考虑地球扁率和田谐摄动项的摄动影响。后续研究可在建模中加入各种摄动项的影响,提高预报精度并减少计算量。此外,对由GPS数据滤波初始化获得的对应时刻的轨道平要素集的初始猜想值也可作进一步优化,以提高初始平要素的准确性。
[1] JOCHIM E F, GILL E, MONTENBRUCK O, KIRSCHNER M. GPS based onboard and on ground orbit operations for small satellites[J]. Acta Astronaut, 1996, 39(9-12): 917-922.
[2] MONTENBRUCK O, GILL E. Orbit determination of the MIR space station using MOMSNAV GPS measurements[C]// 20thInternational Symposium on Space Technology and Science, 11thInternational Symposium on Space Flight Dynamics. [S. l.]: [s. n.], 1996: 96-c-53.
[3] FONTE D. Comparison of orbit propagators in the research and development goddard trajectory determination system (R&D GTDS): partⅠ, simulated data[C]// AAS/AIAA Astrodynamics Specialist Conference. [S. l.]: AAS/AIAA, 1995: 432.
[4] 汤锡生. 载人飞船轨道确定和返回控制[M]. 北京: 国防工业出版社, 2002: 469-472.
[5] 邓自立. 最优估计理论及其应用——建模、滤波、信息融合估计[M]. 哈尔滨: 哈尔滨工业大学出版社, 2005: 98-99.
[6] 张晓坤, 刘迎春, 杨新, 等. 近地卫星星历的高精度星载算法研究[J]. 航天控制, 2005, 23(4): 41-44.
[7] GILL E. GPS-based autonomous navigation for the BIRD satellite: International Symposium on Spaceflight Dynamics[C]// [s. n.]: 2000.
[8] 刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000: 160-164.
[9] 杨维廉. 卫星轨道摄动频谱分析[J]. 宇航学报, 1995, 16(4): 1-8.
[10] 杨维廉. 一种高精度的卫星星历模型[J]. 航天器工程, 1996, 8(2): 21-32.
[11] 林波, 武云丽, 沈莎莎, 等. 轨道误差对星敏感器对地指向精度的影响分析[J]. 空间控制技术与应用, 2013, 39(5): 24-28.
Research of a On-Board Orbit Prediction Method Based on GPS Data
LIU Liao1, SUN Hua-miao1, LI Li-tao2, ZHANG Ying-chun1, 2
(1. Shenzhen Aerospace Dongfanghong HIT Satellite Ltd, Shenzhen 518064, Guangdong, China;2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, Heilongjiang, China)
To improve the capability of micro-satellite orbit prediction, an on-board model of ephemeris parameter was proposed by Kalman filter based on analytic orbit dynamic model and quasi-mean element method without singularity for near circular low earth orbit (LEO), which could estimate the relative ephemeris parameter using GPS data on-orbit. The algorithm flowchart was given. Firstly, the initial state of the filter was judged using external mark. If the initialization was needed, it could be implemented by GPS data, ephermeris parameters upload by the ground or ephermeris parameters obtained in the last filtering. If the initialization had been finished, the ephermeris parameters were treated to gain the new ephermeris parameters by Kalman filtering. The computation modes of orbit predication, residue error calculation, measurement calculation and Bierman-UD decomposing were presented. The simulation results showed that prediction accuracy was better than 20 km in the 7-days prediction for the near circular LEO which the altitude was higher than 450 km. The algorithm proposed had advantages such as self-start (self initialization), good convergence and not ridge requirement of measurement data sampling, which was practicable in engineering.
micro-satellite; self-management; near circular LEO; ephemeris parameter; orbit prediction; GPS data; quasi-mean element; Kalman filter
1006-1630(2017)02-0120-07
2016-08-17;
2016-11-28
国家自然科学基金资助(61473297)
刘 燎(1987—),男,硕士,主要从事微小卫星姿态控制系统设计。
V448.2
A
10.19328/j.cnki.1006-1630.2017.02.013
