基于横滚隔离平台的旋转弹惯导系统实现方法研究

史冉东,郭正勇,杨永强，柴娟芳,高 文

(上海机电工程研究所,上海 201109)



基于横滚隔离平台的旋转弹惯导系统实现方法研究

史冉东,郭正勇,杨永强，柴娟芳,高 文

(上海机电工程研究所,上海 201109)

为实现反舰导弹的可靠拦截并满足导弹小型化及低成本，对一种基于横滚隔离平台的旋转弹惯导系统实现方法进行了研究。采用横滚隔离平台与成像系统消旋平台复用，建立消旋稳定控制系统的模型，经仿真验证了横滚隔离平台能保证惯导系统在较稳定的载体环境中工作。给出了捷联惯导的初始对准算法，选择捷联惯导自对准算法，经分析发现算法的估计与理论分析结果一致。设计捷联惯导解算算法，用单回路等效旋转矢量三子样算法更新姿态矩阵；在杆臂补偿的前提下用四阶龙格-库塔法更新弹体速度与位置，用数字仿真验证了设计的惯导算法能满足导航精度的要求。选取典型弹道进行评估，仿真结果表明，设计的算法精度基本满足工程实现要求，验证了方法的可行性。

旋转弹； 惯导系统； 微电磁系统； 横滚隔离； 消旋稳定； 初始对准； 等效旋转矢量； 四阶龙格-库塔法

0 引言

随着技术的不断发展，反舰导弹作为旋转弹拦截的典型目标之一，其微波和红外辐射特性越来越低特征化，给当前主要以被动微波和红外作为制导模式的旋转弹尽早发现目标带来了很大困难[1]。惯性导航技术自主性强，能全天候工作，不依赖于或受限于外界条件，旋转弹可通过惯性导航与目标预推结合的方式，适应未来拦截目标的需求，实现远距离攻击目标的目的。旋转弹由于其自身体积小的特点，在惯性导航系统设计中除需满足技术可靠的条件外，还受内部空间有限及低成本的制约。目前，旋转弹惯性导航技术主要有基于多加速度计的无陀螺惯性导航、旋转调制式惯性导航和横滚隔离式惯性导航三种[2-6]。无陀螺惯性导航技术解析出的角速度精度低于陀螺输出，且国内外方案都有不同程度的局限性，如数学模型复杂、要求加速度计的动态范围宽、解算误差积累较快、随时间严重发散、工程难以实现等；旋转调制式惯性导航技术要求滚转轴向的陀螺具较大的动态测量范围，对陀螺的量程及精度的要求较高，实现难；横滚隔离式惯性导航技术的特点是惯性导航系统的硬件分布于隔离弹旋的平台上，这样极大降低了滚转通道的动态特性，因此，惯性器件可选择动态范围低且成本低的微机械电子系统(MEMS)器件[6]。根据以上背景，本文对基于横滚隔离平台旋转弹惯导系统的实现进行了研究，采用横滚隔离平台与成像系统消旋平台复用，选用体积小、质量轻、功耗低、适应性强的MEMS器件满足低成本的要求，并研究了与之匹配的初始对准算法和导航解算算法，以在工程中实现旋转弹低成本惯导系统。

1 横滚隔离平台实现方案

横滚隔离平台是一个有理想支撑的单轴稳定平台，当平台基座与载体固联且载体自旋时，平台台体不随载体而转动。但由于工程中平台环架支撑轴承存在摩擦，受摩擦力矩影响，平台不会一直保持稳定。为克服支撑轴摩擦引起的旋转，需设计消旋稳定控制系统，通过安装于平台上的角速度陀螺敏感弹体与电机的速度差(即平台相对惯性空间的滚转角速度)，经控制处理后传送至电机，完全消除弹体对平台的干扰，使横滚隔离平台在旋转轴上相对惯性空间稳定。

1.1 消旋稳定控制系统建模

消旋稳定控制系统主要由敏感元件、稳定对象、控制装置，以及执行元件等部分构成，其结构如图1所示。

对消旋稳定控制系统各组件进行数学建模，可得

a)消旋陀螺模型及参数为

(1)

式中：ωx为陀螺带宽；ξx为陀螺阻尼系数；s为拉氏算子。

b)消旋控制(功放及校正网络)模型及参数为

(2)

式中：KP，KI，KD分别为校正网络的比例、积分和微分系数。

c)力矩电机模型及参数为

(3)

式中：Rx为消旋电机电枢绕组的电阻；Tmx，Cmx分别为消旋电机的电气时间常数和力矩系数。

d)横滚隔离平台模型及参数为

(4)

式中：Jx为平台转动惯量；bx为平台阻尼系数。

1.2 消旋稳定控制系统仿真

为验证该消旋稳定控制系统的性能，在弹旋10 r/s(即62.5 rad/s)输入条件下仿真所得横滚隔离平台在消旋稳定控制系统作用下的输出如图2所示。图2中：弹体转速表示旋转导弹对弹旋指令62.5 rad/s的响应；平台转速和平台转角表征平台对指令的响应。仿真结果表明：平台转速阶跃响应调节时间小于0.2 s，超调量不超过0.2%，稳态误差为零，即横滚隔离平台能保证惯导系统在较稳定的载体环境中工作。

2 捷联惯导初始对准

按捷联惯导初始对准从是否利用外部测量信息的角度，可分为自对准和传递对准。由计算机处理陀螺和加速度计的测量输出值，解算出姿态阵和速度误差，并从速度误差中估计出失准角。待失准角估计达到稳态后，用失准角估计值对姿态阵作校正，完成初始对准，此为自对准。传递对准则由高精度的主惯导提供姿态阵和速度、位置信息，对子惯导进行装订，子惯导以此装订值作为姿态阵的初始值并开始姿态计算和导航解算。在解算过程中，用卡尔曼滤波算法估出失准角的实时值，待估值达到要求的精度后，对实时解算的姿态阵作一次修正。

由于旋转弹武器系统反应时间快，作战准备时间短，而传递对准所需时间一般较长，不能满足要求，因此本文选择自对准算法。自对准算法一般包括粗对准和精对准两个过程，其中粗对准只在外界无俯仰角装订条件下启用。具体误差模型如下[7-12]。

2.1 粗对准算法

粗对准一般根据加速度计和陀螺的静态输出由解析的方法完成。设加速度计的输出为fb，陀螺的输出为ωb，则为获得初始姿态矩阵，理论上可构造关系式

(5)

(6)

此处：

其中：ϑ，ψ，γ分别为平台的俯仰角、偏航角和滚转角。

因静态时陀螺测量值较小，故陀螺误差对估算精度影响较大。数字仿真估算当陀螺误差1 (°)/h时，方位角误差约6°。因此，方位角无法通过粗对准获得，还需外界装订。根据

(7)

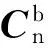
(8)

2.2 精对准算法

2.2.1 误差方程

速度及其误差方程可表示为

(9)

姿态及其误差方程可表示为

(10)

2.2.2 数学模型

精对准采用传统Kalman滤波，并以北向和东向两个速度作为观测量，模型如下。

a)对准方程定义

(11)

式中：X=[δvnδveΦnΦuΦe]T；F为状态转移阵；W为系统噪声阵；Z为系统观测量；H为观测阵；V为观测噪声阵。此处：δvn，δve分别为北向和东向速度误差；Φn，Φu，Φe分别为北向、天向、东向失准角。

b)状态转移矩阵更新

(12)

式中：fU，fN，fE分别为惯测输出的瞬时量在导航坐标系中的分量；ve，vn，vu分别为载体所在点处的东向、北向和天向速度；RM，RN分别为子午圈和卯酉圈的曲率半径；L为载体所在点的纬度；

此处：ΩN=ωiecosL；ΩU=ωiesinL。其中：ωie为地球自转速率。

c)F，W离散化

(13)

式中：T为计算周期；I为单位阵；Q为离散前的系统噪声阵。

d)观测量更新

(14)

式中：Zvn=vn+Δvn；Zve=ve+Δve。此处：vn，ve为每次对准滤波开始时导弹惯导输出的速度；Δvn，Δve为系统的观测噪声。

e)滤波更新

(15)

将惯测输出的噪声近似视作白噪声，则R为式(11)中V的方差阵。

2.3 算法验证

设数字仿真条件为：初始对准时间t0=0；初始纬度L=31°；导弹初始速度vE=0 m/s，vN=0 m/s；精对准初始失准角φE=1.2°，φN=0.8°，φU=1°；卡尔曼滤波器初始值

Q=

diag[(σaN)2(σaE)2(σgN)2(σgU)2(σgE)2]

R=diag[(σvN)2(σvE)2]

(σvN)2=(σvE)2=(0.1)2

理论分析误差角估计偏差为

(16)

式中：Φe_e，Φn_n分别为东向和北向误差角。仿真所得精对准估计误差角和初始对准前后导航精度分别如图3、4所示。仿真结果表明：估计偏差0.2°(1σ)，与理论分析基本一致。

3 捷联惯导解算算法

3.1 姿态矩阵更新

捷联惯导姿态矩阵更新算法一般有欧拉角法(三参数法)、四元数法(四参数法)和方向余弦法(九参数法)三种，本文采用四元数法进行求解[13]。一般，旋转弹的过载能力要求高，弹体动态特性变化大，还会出现弹道螺旋运动。高动态引入的关键问题是：在用毕卡算法求解四元数微分方程时使用了陀螺角增量输出，角增量虽微小，但不能视为无穷小，而在刚体作有限转动时，刚体的空间角位置与旋转次序有关，即存在刚体转动引起的不可交换误差(又称圆锥误差)，它是姿态解算的一个主要误差源。为补偿姿态解算中因旋转弹线振动和角振动产生的圆锥误差，本文用多子样旋转矢量算法求解四元数微分方程[14]。从算法本质看，旋转矢量算法的子样数越多，姿态更新计算越准确，但计算量也随之增大。等效旋转矢量的单回路算法如下。

旋转矢量微分方程可简单描述为

(17)

式中：Φ为载体坐标系角位置变化对应的等效旋转矢量。

等效旋转矢量的单回路算法是指在一个姿态更新周期内，旋转矢量的求解和姿态更新计算均发生在姿态更新时间点上，其流程如图5所示。根据在姿态更新周期内对陀螺输出角增量等间隔采样数的不同，等效旋转矢量的求解分为单子样法、双子样法和三子样法等。

设Φ(h)为时间段[tk，tk+1]内的等效旋转矢量，此处h=tk+1-tk。设τ为时间增量，当采用常数拟合角速度时，等效旋转矢量单子样法为

(18)

式中：Δθ为时间段[tk，tk+1]内的角增量；a为待定参数。

当采用直线拟合角速度时，等效旋转矢量双子样法为

(19)

式中：Δθ1，Δθ2分别为时间段[tk，tk+h/2]，[tk+h/2，tk+1]内的角增量；b为待定参数。

当采用抛物线拟合角速度时，等效旋转矢量三子样法为

(20)式中：Δθ1，Δθ2，Δθ3分别为时间段[tk，tk+h/3]，[tk+h/3，tk+2h/3]，[tk+2h/3，tk+1]内的角增量；c为待定参数。

因旋转弹的角运动具很大任意性，故用任何曲线进行拟合角速度都会有一定的误差。鉴于旋转弹末端防御过程中，针对大机动目标可能导致角运动变化激烈，而高子样算法的精度优于低子样算法的特点，本文选择单回路等效旋转矢量三子样法算法作为求解姿态四元数的方法。

3.2 弹体速度及位置更新

(21)

式中：rB为惯测装置与导弹质心的距离；下标i表示相应矢量在惯性坐标系中的分量。将式(21)右端的修正项展开，可得

(22)

将载体视作刚体，则惯测组件安装点在载体系中固定，式(22)可简化为

(23)

由叉乘原理可得

(24)

式中：

杆臂长度包括外杆臂长度和内杆臂长度，一般称惯导内三个加速度计质点至导航参考点的矢量长度为外杆臂或杆臂，惯导三个加速度计敏感点至惯导质点的距离为内杆臂，其对系统的影响称为尺度效应。内杆臂或外杆臂，当惯组有角速率时加速度计敏感到附加比力的机理相同。杆臂效应补偿的关键是确定杆臂长度，旋转弹因其结构复杂，杆臂长度难以直接测量，故用静态试验法分别测量两组同一时刻的加速度计实际输出，再用姿态矩阵解出杆臂长度。

3.3 惯导算法验证

选取无控弹道，设导弹俯仰发射角20°、偏航发射角10°，在不进行舵机控制的情况下飞行10 s，在不加入误差的条件下对本文设计的惯导算法进行仿真验证，所得解算误差如图6所示。仿真结果表明：设计的算法可满足导航精度的要求。

4 仿真及分析

取典型弹道为：遭遇距离7 km；发射距离15.1 km；速度700 m/s；高度10 m；航路1 km；遭遇时间10.2 s。将精对准仿真结果代入进行仿真，所得理论弹道与解算值如图7所示。仿真结果表明：本文设计算法可满足工程实现精度的要求。

5 结束语

针对旋转弹空中交班中的核心，本文研究了初制导段惯导系统的设计方法。基于横滚隔离系统原理，给出了数学模型及硬件实现过程，通过数字仿真验证了横滚隔离系统的性能，结果表明横滚隔离系统可保证平台相对惯性空间的稳定，能为MEMS惯性导航系统用于旋转弹提供稳定的载体环境。本文实现了惯性导航初始对准算法，在外界无俯仰角装订时用粗对准确定旋转弹的初始姿态，有初始姿态装订时直接进行精对准计算。建立了粗对准与精对准数学模型，并通过仿真验证了精对准算法精度与理论计算精度的一致性。本文给出了惯性导航解算算法。针对旋转弹飞行过程中的弹道螺旋运动，用单回路等效旋转矢量三子样法算法求解四元数，极大地减少了不可交换误差对弹体姿态更新的干扰；对惯性器件安装位置与导弹质心间的杆臂效应，进行了杆臂补偿，降低了初始位置对导航解算的影响。用末端防御中的一个典型弹道对基于横滚隔离平台的旋转弹惯性导航算法进行评估，结果表明本文算法精度基本满足要求。惯性导航在旋转弹上的实现，为远距离攻击新型反舰弹的实现提供了基础，为顶层设计和相关设计提供了依据和方向。后续将对缩短初始对准的时间进行研究，不断完善等效旋转矢量参数设计及杆臂效应补偿，进一步减小惯性导航系统的误差。

[1] 谢浩怡， 赵良玉， 石忠佼. 旋转弹解耦控制方法综述[J]. 战术导弹技术， 2015(1)： 73-78.

[2] 郝宏伟. 小直径高速旋转弹姿态参数测试技术研究[D]. 太原: 中北大学, 2009.

[3] 史震. 无陀螺捷联惯导系统中加速度计配置方式[J]. 中国惯性技术学报， 2002， 10(1)： 15-19.

[4] 陈可, 朱春云, 于华男. 旋转弹用MEMS惯导自主误差抑制方法[J]. 战术导弹技术, 2012(6): 79-85.

[5] KIM J, CHOI H D, LEE J H. An anti-wind-up controller design for rocket control systems with control input saturation[J]. ImechE, 1998, 212(G): 261-269.

[6] IMBAULT J J, TJULIN H, KOHLER S. Mini-RIMS: a miniature roll-stabilized inertial measurement system[C]// AIAA Conference on Sounding Rockets, Balloons and Related Space Systems. [S. l.]: [s. n.], 1986: 35-43.

[7] 牟淑志， 卜雄洙， 李永新， 等. 高转速载体惯性测量组合研究[J]. 弹道学报， 2006， 18(4)： 579-603.

[8] 任蕾. 捷联惯性导航系统初始对准方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.

[9] 聂莉娟. 捷联惯导系统初始对准滤波技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2004.

[10] 张德明. 舰载武器惯导系统初始对准技术研究[D]. 沈阳: 沈阳理工大学, 2011.

[11] 程向红, 郑梅. 捷联惯导系统初始对准中Kalman参数优化方法[J]. 中国惯性技术学报, 2006, 14(4): 12-17.

[12] 王业卿， 黄建新， 杨雨， 等. 红外旋转弹导引头捷联惯导系统的姿态算法研究[J]. 上海航天， 2016, 33(3):36-42.

[13] 邓亚隆. 惯性技术[M]. 哈尔滨：哈尔滨工业大学出版社, 2006.

[14] 秦永元. 惯性导航[M]. 北京： 科学出版社， 2006.

Study on Implementation Method of Roll-Isolated Inertial Navigation System Based on Spinning Projectile

SHI Ran-dong, GUO Zheng-yong, YANG Yong-qiang, CHAI Juan-fang, GAO Wen

(Shanghai Electormechanical Engineering Institute, Shanghai 201109, China)

To realize the interception of anti-ship missile reliably and meet the constrain of limited space inside the spinning projectile and cost, an implementation method of inertial navigation system based on roll-isolated platform was studied in this paper. The roll-isolated platform was reused with despun stability control system for imaging. The model of the despun stability control system was established. The simulation result showed that the roll-isolated platform could ensure that the inertial navigation system would work in the stable environment. The initial alignment algorithm of strapdown inertial navigation system was given. The simulation results showed that the estimation obtained by the algorithm proposed was agreed with the theory. The solution algorithm of the strapdown inertial navigation system was designed. The attitude matrix was renewed by three samples of single loop equivalent rotation vector, and the velocity and position of the spinning projectile were renewed by the forth order Runge-Kutta methods. The lever arm effect was compensated. The simulation result showed that the algorithm of the strapdown inertial navigation system proposed could meet the accuracy requirement of navigation. Finally a typical trajectory was used to assess the system designed. It found that the accuracy of the algorithm proposed could meet the accuracy in engineering. The feasibility of the algorithm was approved.

spinning projectile; inertial navigation; micro-electro mechanic system; roll-isolated; despun stability; initial alignment; equivalent rotation vector; forth order Runge-kutta methods

1006-1630(2017)02-0161-08

2016-08-11；

2016-10-17

国防预研项目

史冉东(1990—)，男，硕士，主要从事旋转弹惯性导航技术研究。

V249.322

A

10.19328/j.cnki.1006-1630.2017.02.018