基于PD控制的大挠性卫星输入成型姿态机动方法研究
2017-04-28吴敬玉陆智俊
钟 超,吴敬玉,陆智俊
(上海航天控制技术研究所,上海 201109)
基于PD控制的大挠性卫星输入成型姿态机动方法研究
钟 超,吴敬玉,陆智俊
(上海航天控制技术研究所,上海 201109)
对有快速姿态机动要求的大挠性卫星,为减小挠性振动对姿态机动时间的影响,对基于比例微分(PD)控制的输入成型姿态机动方法进行了研究,提出用输入成型方法在快速机动过程中直接对附件的挠性振动进行抑制。将动力学方程扩展到状态空间,通过求解状态矩阵的特征值解出系统的等效振动频率与阻尼比,以获得成型输入器。给出了一种简化的且能满足工程使用的输入成型频率参数确定方法。设计了输入成型的PD控制器,实现欧拉轴快速姿态机动,同时有效抑制附件的振动。对输入成型器的误差进行了分析。仿真分析了ZVD,EI,ZVDD,EI-Twohump四种输入成型器对某卫星太阳阵挠性振动的抑制效果,以及惯量和挠性参数分别在标称及拉偏状态下卫星姿态机动时的姿态误差与振动模态。结果表明:该方法可满足工程使用要求,简易地获取输入成型参数,设计绕欧拉轴近似最短路径的机动方式,能有效抑制附件的挠性振动,实现快速的姿态机动。
大挠性卫星; 输入成型; PD控制; 姿态机动; 挠性参数; 姿态控制; 带宽隔离; 挠性抑制
0 引言
随着卫星功能的增强,有效载荷增加,为保证星上能源的供应,太阳能帆板的面积需相应增大,卫星的动力学特性表现为星体大惯量和附件大挠性。对无姿态机动要求的大挠性卫星,姿态控制器都是通过减小系统带宽的方法减弱附件挠性振动对控制系统的影响[1-8]。对有快速姿态机动要求的卫星,执行机构输出的大力矩易激发挠性附件振动,从而对姿态机动过程的快速与稳定造成影响,进而影响姿态机动时间。
对大挠性附件卫星控制的研究主要有频率隔离、变结构控制和分力合成等方法。频率隔离法属被动控制方法,简单易行,但随着技术的发展,对卫星姿态机动提出了新的要求,而该方法难以满足这些新要求[8]。变结构控制方法对系统参数和干扰有较强的鲁棒性,但需利用全状态信息反馈,而卫星上挠性部件的模态振动一般难以通过测量得到[9-11]。分力合成方法可有效抑制挠性附件的振动,但需准确获知挠性附件的挠性参数,对参数的鲁棒性较差,但航天器准确的在轨挠性参数无法获得[12-13]。
输入成型方法是指由脉冲序列与给定的期望输入卷积,形成的成型输入信号作用于被控对象。输入成型是一种减小系统余振的前馈控制,通过合理设计这些脉冲的大小及时间可消除残余振动[14-16]。输入成型控制设计需求取整星的非约束模态挠性参数。卫星动力学按状态空间改写后,将面临从高阶矩阵中求取对应的整星等效挠性参数的问题,其计算非常复杂且量大,不利于工程实现[17-19]。
本文将输入成型方法与PD控制结合,设计了一种易于工程使用同时又能满足工程要求的输入成型器挠性参数获取方法。根据多挠性体动力学输入成型设计方法,先将动力学方程扩展至状态空间,由状态矩阵的特征值解出系统的等效振动频率与阻尼比;在分析状态矩阵的基础上,给出了一种误差范围在工程中可接受的系统特征值求取方法;设计了跟踪期望轨迹的PD控制方法。此外,还设计了添加输入成型的绕欧拉轴快速机动的控制器,能在实现快速机动的同时有效抑制附件的振动。最后用数学仿真对本文方法在姿态机动过程中抑制挠性附件振动的有效性进行验证。
1 输入成型方法
输入成型方法是一种通过对输入力矩信号进行某种改变,在力矩输入完成后能保证卫星机动指定角度,同时使卫星的柔性附件没有残余振动的方法。通常来讲,输入成型器相当于一个滤波器,可将输入力矩中与帆板振动频率相同的信号滤除,从而避免卫星在机动过程中激发帆板振动。
卫星的动力学模型可表示为
(1)
式中:φ为卫星的三轴姿态角;I为卫星惯量;T为控制力矩;a为刚柔耦合系数;η为挠性附件的模态坐标;ωc为挠性振动的频率;ξ为模态振动阻尼比。
首先,考察单位脉冲力矩激发的挠性附件的振动。将挠性附件的振动方程改写为
(2)
将控制力矩T视作零初始条件下的一系列的脉冲输入,则可得系统的响应
(3)
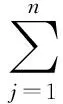
展开式(3),并令其中含有时间项的系数为零,则可得
(4)
(5)
求解式(4)、(5)可得作用于卫星的n个脉冲力矩的Aj,tj,并能保证在第n个脉冲力矩作用后系统的残余振动为零。
对实际卫星,帆板的振动频率和阻尼比常存在一定的拉偏,常用的方法是引入约束方程
(6)
使成型器对不确定性具有一定的鲁棒性。N的数值不同,成型器的名称也不相同,称为N阶鲁棒输入成型器。当卫星携带帆板1个,但帆板有振动频率m个时,可分别对各阶振动频率求解输入成型器,最后将所得成型器进行卷积以得到新的成型器,新的成型器能抑制上述m个频率的振动。
目前应用较广的成型器有ZD,ZVD,ZVDD,EI,EI-Twohump成型器。ZD成型器是双脉冲成型器,该成型器适于无频率拉偏状况,能精确抑制振动。当存在频率拉偏时,ZD成型器的残余振动过大,不具有很好的鲁棒性。ZVD,ZVDD成型器通过对残余振动的导数进行限制以增强控制器的鲁棒性,但这会增加成型器的长度,如ZVDD成型器的长度为ZD成型器的两倍。EI,EI-Twohump成型器都有更好的鲁棒性,在标称状态下允许有误差存在,但当频率偏离标称状态一小段距离时,残余振动幅值减小;当频率偏差达到一定值时,系统的残余振动为零。EI,EI-Twohump成型器正是利用这种方法增强鲁棒性的。
1.1 ZD,ZVD,ZVDD成型器
传统输入成型方法通过求解约束表达式(4)、(5),使n个脉冲作用过后,系统的残余振动为零。令n取极小值,求解上述的约束方程。
通过优化方法可得,此成型器的最小脉冲数为2个,其作用时间与幅值见表1。

表1 ZD成型器参数Tab.1 Parameters of ZD input shaper
表1中,K,t满足关系
(7)
为增加系统的鲁棒性,增加以下约束条件
(8)
由此则得到ZVD成型器。式(8)约束了脉冲结束时刻系统残余振动的变化率,系统残余振动的变化率最小,从而增加了系统的鲁棒性。ZVD成型器参数见表2。
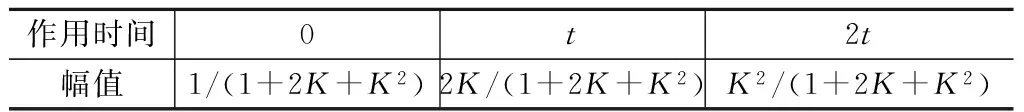
表2 ZVD成型器参数Tab.2 Parameters of ZVD input shaper parameters
为使系统的鲁棒性更强,常采用以下约束
(9)
由此得到ZVDD输入成型器。式(9)不仅约束了残余振动的一阶导数,而且对二阶导数也进行了限制。ZVDD成型器参数见表3。
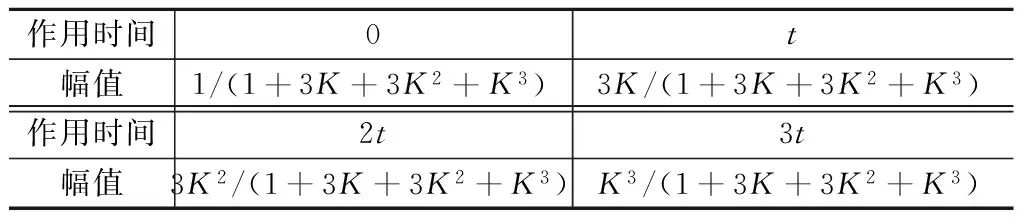
表3 ZVDD成型器参数Tab.3 Parameters of ZVDD input shaper
理论上可无限制地增加约束条件,从而使成型器获得更强的鲁棒性,但过长的成型器并不合适。此外,限制残余振动的更高阶导数对系统鲁棒性的影响并不明显。因此,实际应用最广的是ZVD,ZVDD成型器。
1.2 EI,EI-Twohump成型器
EI成型器是在研究ZVD成型器向量图的条件下提出的。对ZVD成型器的相位进行微小的调整能较好地提高系统的鲁棒性,但这种鲁棒性有方向性,即对某个方向拉偏的频率偏差有较强的鲁棒性。
EI成型器参数见表4。表4中:A1~A3满足关系
(10)
式中:V为标称状态时系统的残余振动幅值。
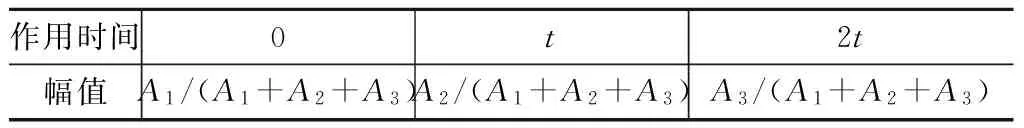
表4 EI成型器参数Tab.4 Parameters of EI input shaper
EI-Twohump成型器是对4个脉冲的ZVDD方法改进后得到的。其约束条件是:标称频率时系统无残余振动,在标称频率的两边存在对称的两点,在这两点上系统的残余振动为允许的最大值;在这两点的外部存在另外两个对称点,这两个点的残余振动为零。这种振动形式是在允许条件下4个脉冲能达到最大鲁棒性的脉冲形式。
EI-Twohump成型器参数见表5。

表5 EI-Twohump成型器参数Tab.5 Parameters of EI-Twohump input shaper
表5中:A1~A4满足关系
(11)
两种脉冲数最多的输入成型器的鲁棒性如图1所示。
2 多挠性附件动力学输入成型器设计
2.1 输入成型器求取
携带多个挠性附件的卫星动力学模型可表示为
(12)
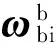
设挠性附件有振动频率m个,将式(12)写成状态空间形式
(13)
式中:A,B分别为(2nm+6), (2nm+6)×3维的常值矩阵,A,B的具体表达式对推导过程无影响;
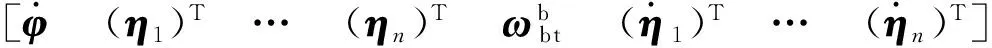
(14)
式中:x0为系统的初始状态。一般,对姿态机动控制问题,系统的初始状态为零,则得
(15)
式中:uj为第j个脉冲输入。为在机动结束后有效消除振动,需式(15)在t>tn时恒为零。式(15)改写为
(B1uxj+B2uyj+B3uzj)=0
(16)
式中:Bi为矩阵B的第i列;uxj,uyj,uzj分别为第j个脉冲力矩在x、y、z轴的分量。
需说明的是,因无法事先知道三轴控制力矩的比例,故不能通过对某一轴力矩的成型消除另一轴的振动,需分别对三轴力矩进行成型处理。
不失一般性,以滚动轴为例,根据成型器条件推导,若A含有不同的特征值n个,则式(16)中的e-A(t-tj)可写成
(17)
式(17)中P的第i列是A的第i个特征值对应的特征向量。则式(17)可化简为
(18)
对简单的无耦合的二阶系统,可在时域内得到简单的输入成型器的约束方程,约束方程可写成式(18)的形式,式(18)中的特征值恰好对应于各二阶系统的频率与阻尼比。
因此,对有多个挠性附件的系统,只需将其写成状态空间的形式,并求解A的特征值,就可通过A的特征值解出系统的等效振动频率与阻尼比,进而根据等效振动频率与阻尼比求解成型器。除与控制器对应的6个特征值外,其余的特征值是与附件的运动相对应的,振动系统的特征值成对出现,并互为共轭。一对共轭特征值可求解出一个等效的振动频率和阻尼比。共轭特征值与等效振动频率、阻尼比的满足关系
(19)
式中:λ为振动系统的特征值;i为虚数单位。由式(19)可求出振动系统的等效振动频率和阻尼。
2.2 挠性附件等效振动频率工程简化求取
A与挠性附件的耦合系数有关,而耦合系数在附件转动时会发生变化,因此其特征值的求取有一定难度。本文推导了一种误差范围在工程中可接受的特征值求取方法。
将卫星姿态控制系统写成状态空间的形式,其表达式为
(20)
式中:
x=
(21)
A=
(22)
(23)
此处:Ic=I-Brot·(Brot)T;H=(E-(Brot)TI-1Brot)-1;q#=0.5(q0E3+(qv)×);E为对应维数的单位矩阵;qv为四元数矢部;符号“”表示反对称阵。
将PD控制器代入式(20)可得
(24)
式中:qvd为期望四元数矢部;Kp,Kd分别为控制器的比例系数和微分系数;ad为期望角加速度;e为欧拉轴。另
(25)
此处:
仅需求取出A*的所有特征值,并分离出其中与挠性附件振动频率对应的特征值即可应用输入成型方法。但通常控制系统的运动学方程是非线性的,即A*的表达式中含有q#项,因此无法精确得到A*的特征根。
分析A*特征根的形式,并讨论非线性运动学方程对挠性振动对应的特征根的影响。考虑一般的控制形式,则
(26)
式中:q0为姿态四元数的标部。在卫星机动过程中,q0随时间而变,其变化范围为0~1。
以某卫星为例分析q0变化对A*中对应的挠性附件振动频率的影响。卫星太阳电池阵的1~6阶模态频率分别为 0.181,0.589,0.909,0.993,2.402,2.726 Hz;X侧太阳电池阵振动与转动的柔性耦合系数矩阵分别见表6、7。
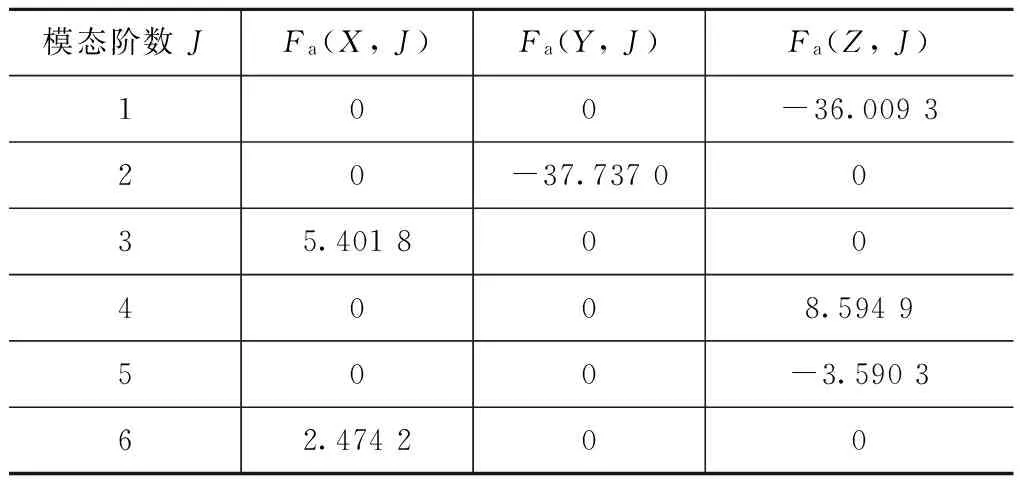
表6 +X侧太阳电池阵振动与转动的柔性耦合系数矩阵Tab.6 Vibration and flexible coupling coefficient array of +X side solar cell array
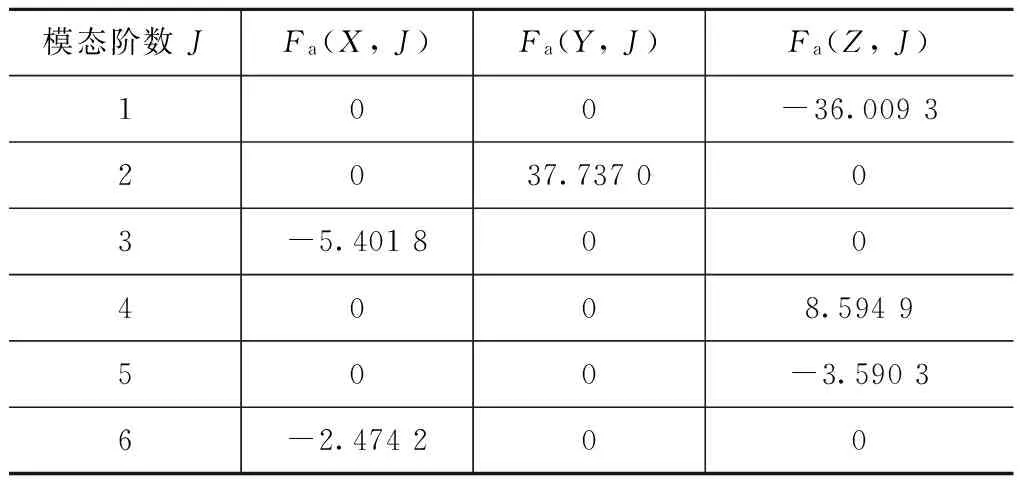
表7 -X侧太阳电池阵振动与转动的柔性耦合系数矩阵Tab.7 Vibration and flexible coupling coefficient array of -X side solar cell array
将上述参数代入式(26),计算挠性附件对应的频率,与用简化矩阵计算的附件振动频率进行对比,分析附件频率计算的误差,以及q0变化对计算结果的影响,误差分析结果见表8。计算中,Kp=0.04,Kd=0.4。
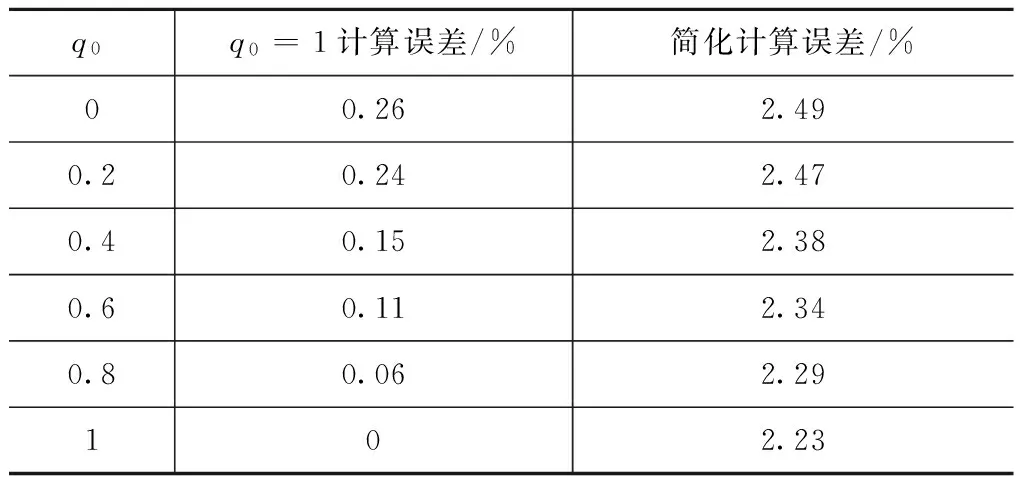
表8 特征值误差Tab.8 Error of eigenvalue
由表8可知:q0的变化对A*附件振动频率的影响很小,最大影响相当于附件频率拉偏了0.26%。简化计算的结果与实际的振动频率偏差约2.49%,对比卫星实际振动频率的拉偏,2.49%的计算误差可接受。
3 PD控制器设计
本章设计了一种输入成型的PD控制快速姿态机动方法,该法适于绕欧拉轴机动的卫星,并可抑制机动过程中激发的振动,同时能获得姿态快速稳定的效果。
为实现卫星的快速姿态机动,可先规划出一条期望的欧拉角速度ωd与期望的欧拉角轨迹Φd,用PD控制算法使卫星状态跟踪这个期望的状态。为使系统能同时跟踪上期望的欧拉角速度与欧拉角,ωd,Φd应满足关系
(27)
为使系统能精确跟踪期望的姿态与姿态角速度,在一般PD控制器的基础上引入沿欧拉轴的ad的前馈,ad,ωd需满足条件
(28)
利用第2章中得到的输入成型脉冲序列F,将规划的路径与其进行卷积处理得到成型后的期望路径,即
(29)
根据期望欧拉角计算出qvd,其表达式为
(30)
式中:e0为机动欧拉轴。
含有期望角加速度前馈的PD跟踪控制算法为
ade0)
(31)
直接用式(31)控制方式即可对卫星姿态进行控制,能保证在机动结束后没有因姿态机动而留下的残余振动。因振动在机动后被有效抑制,故可将系统的带宽设计得更大,使其能精确跟踪轨迹Φd,ωd。
4 输入成型器误差分析
对实际的卫星姿态控制系统,输入成型器并不能在机动结束后完全消除附件的振动,主要原因如下。
a)实际的控制系统为离散控制系统,因离散时间是固定的,故无法保证输入成型器延时的准确性,这样会造成时间上的误差。如振动的半周期小于离散系统的时间,将无法应用输入成型控制器。
b)实际的帆板振动频率存在偏差,与标称的振动频率并不严格相同,这将会导致实际的振动抑制效果偏离理论结果。
c)由于转动惯量与卫星的帆板振动频率有关,转动惯量的拉偏将会影响帆板的实际振动频率,其效果相当于振动频率的拉偏。
d)若机动过程中帆板发生转动,则需在理论上说明帆板转动对卫星振动抑制的影响。
首先分析原因b)、c)。帆板振动频率拉偏产生的偏差可直接转化为成型器时间节点的不准确。这样转化的根据是:在成型器的两个参数(脉冲幅值与作用时间)中,只有作用时间是振动频率的函数,由式(7)可知:脉冲幅值是关于K的函数,作用时间是关于t的函数,振动频率的拉偏将导致脉冲作用时间不准确。但这可通过应用鲁棒性更强的输入成型器尽量减小由振动频率拉偏带来的影响。
其次分析原因a)。这相当于将脉冲作用时间延后,脉冲作用时间变为实际脉冲作用时间后且距其最近的离散时间整数倍的时间点。如离散时间为0.5 s,脉冲作用时间为2.6 s,则实际的脉冲作用时间为3 s。这种由离散化造成的脉冲作用时间的不确定性可转化为振动频率的不确定,相当于振动频率正向拉偏。对一阶频率,相当于挠性频率5%之内的拉偏。
最后分析原因d)。对帆板的耦合矩阵参数进行分析可知:帆板转动对卫星振动频率的影响很小,而耦合系数的变化将导致脉冲作用时间点的输入矩阵B不同,这样导致的等效变化相当于脉冲幅值发生了变化;但若帆板的转动速度较慢,则B的变化速度也相对较慢,这样在两个脉冲作用时间间隔内B的变化就非常小,因此对振动抑制效果的影响也就非常小。
5 仿真
本文以某卫星为例进行仿真。该卫星太阳电池阵展开后的面积31 m2,第一阶模态0.181 Hz,第二阶模态0.589 Hz,姿轨控分系统采用角动量50 N·m·s的五棱锥构型控制力矩陀螺群作为执行机构,需绕滚动方向在180 s内机动66°,姿态机动结束指标为姿态角小于0.02°,姿态角速度小于0.000 5 (°)/s。
由于采用控制力矩陀螺群作为执行机构,输出力矩达到10 N·m,此大力矩作用于卫星上,姿态机动时电池阵挠性模态激发严重,无法满足姿态机动时间的指标要求。取整星的惯量参数为:Ixx=8 063 kg·m2;Iyy=14 784 kg·m2;Izz=12 225 kg·m2;Ixy=-368 kg·m2;Iyz=2 657 kg·m2;Ixz=345.6 kg·m2。PD控制器参数设计为:无阻尼角频率ωn=0.2 rad/s;阻尼比ξ=0.9;最大机动角速度ωn=0.8 (°)/s;欧拉轴方向最大力矩Tx=10 N·m。
因系统控制周期0.5 s,离散时间较长,仅能对一阶与二阶振动频率产生一定的抑制作用,故只设计了抑制一阶、二阶频率的ZVD、EI、ZVDD、EI-Twohump输入成型器,各成型器参数见表9~12。期望轨迹时间节点见表13。

表9 ZVD输入成型器参数Tab.9 Parameters of ZVD input shaper

表10 EI输入成型器参数Tab.10 Parameters of EI input shaper

表11 ZVDD输入成型器参数Tab.11 Parameters of ZVDD input shaper

表12 EI-Twohump输入成型器参数Tab.12 Parameters of EI-Twohump input shaper

表13 期望轨迹时间节点Tab.13 Anticipant track time node
5.1 输入成型方法比较
分别用ZVD,EI,ZVDD,EI-Twohump输入成型器进行姿态机动控制仿真,所得两翼太阳电池阵的挠性模态激发分别如图2~9所示,对太阳阵残余振动的抑制结果见表14。
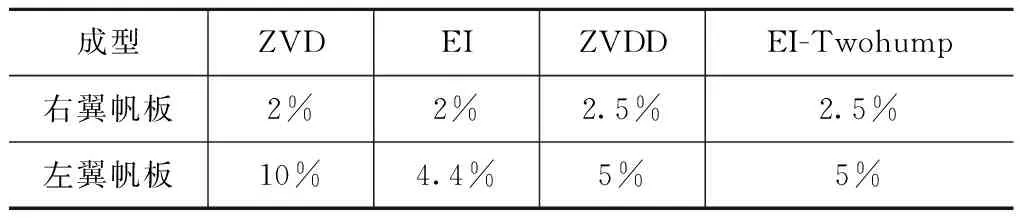
成型ZVDEIZVDDEI-Twohump右翼帆板2%2%2.5%2.5%左翼帆板10%4.4%5%5%
由表14可知:ZVDD,EI-Twohump输入成型方法对太阳阵挠性振动的抑制效果相当,且均优于EI,ZVD输入成型方法,ZVD输入成型方法的抑制效果最差。
5.2 姿态机动仿真
用Matlab/Simulink软件编制仿真程序,针对PD控制的跟踪输入成型轨迹方法进行仿真,采用ZVDD输入成型方法。采用ODE4算法,取积分步长0.02 s,仿真时长6 000 s,在时刻2 000 s机动。惯量和挠性参数为标称值时,仿真所得姿态角误差、姿态角速度误差、两翼帆板振动模态分别如图10~15所示。
帆板模态频率拉偏+20%时,仿真所得姿态角误差、姿态角速度误差、两翼帆板振动模态分别如图16~21所示。
帆板模态频率拉偏-20%时,仿真所得姿态角误差、姿态角速度误差、两翼帆板振动模态分别如图22~27所示。
惯量拉偏+15%、帆板模态频率拉偏+20%、耦合系数拉偏-20%时,仿真所得姿态角误差、姿态角速度误差、两翼帆板振动模态分别如图28~33所示。
惯量拉偏-15%,帆板模态频率拉偏-20%,耦合系数拉偏+20%时,仿真所得姿态角误差、姿态角速度误差、两翼帆板振动模态分别如图34~39所示。
在标称和上述不同拉偏条件下,仿真所得姿态控制和挠性模态振动幅值见表15。
5.3 仿真小结
由图10~15可知:采用本文简化的输入成型参数获取方法,结合跟踪期望轨迹的PD控制算法,在标称的惯量和挠性参数条件下,姿态机动结束用时131 s,远优于总体对姿态机动的指标要求(180 s)。与其它方法相比,本文提出的设计方法可有效抑制姿态机动过程中的挠性模态激发,缩短了姿态机动时间。
由表15可知:在各种参数拉偏情况下,系统的控制精度和稳定度一致,但姿态机动时间和模态抑制程度相当,姿态机动时间最大136 s,最小123 s,相差不大,对应的挠性模态振幅分别为0.25,0.009。由此可认为,本文提出的方法能适应卫星惯量参数和附件模态的拉偏,具一定的鲁棒性,可满足工程应用。
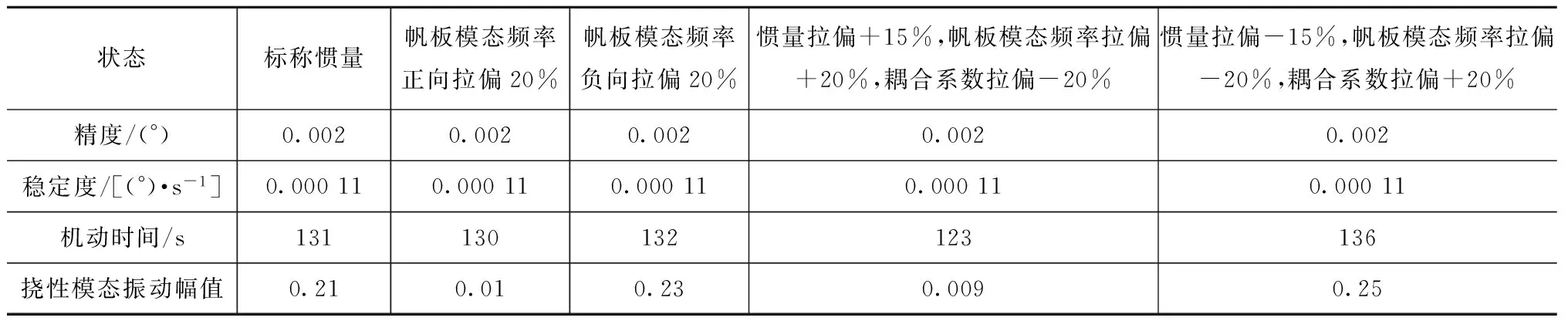
表15 姿态控制和挠性模态振动幅值Tab.15 Attitude control and flexible modal vibration range
6 结束语
本文针对卫星控制系统进行状态空间建模,从理论上推导出了系统设计输入成型器时等效频率与状态矩阵的关系,结合PD控制器的形式,设计了一种误差范围在工程中可接受的简单的特征值求取方法。将输入成型器的脉冲对姿态机动路径进行卷积处理得到期望的轨迹,设计了跟踪期望轨迹的PD控制方法。以某卫星为背景进行了数学仿真,结果表明:采用该方法后姿态机动过程中附件的挠性振动被有效抑制,姿态机动时间远优于技术指标的要求。分析仿真可知:该方法对参数的拉偏具鲁棒性,能适应惯量参数±15%、帆板挠性模态参数±20%的拉偏。
本文方法依赖于地面整星惯量和挠性参数的准确测量,如整星参数的地面测量误差较大,输入成型器所需的等效频率就会产生较大的误差,这会对控制效果产生一定影响。后续将对在轨整星惯量和挠性参数的辨识进行研究,以获得较准确的辨识参数,用辨识参数对输入成型器和PD控制器进行修正,期望获得更好的控制效果。
[1] 章仁为. 卫星姿轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 2006.
[2] SINGHOSE W E, BANERJEE A K. Flexible spacecraft with deflection-limiting input shaping[J]. Journal of Guidance, Control, and Dynamics, 2015, 20(2): 291-298.
[3] 原劲鹏, 杨旭, 杨涤. 输入成型在卫星喷气姿态机动控制中的应用[J]. 东南大学学报, 2005, 35(S2): 137-141.
[4] 刘刚, 李传江, 马广富, 等. 应用SGCMG的卫星姿态快速机动控制[J]. 航空学报, 2011, 32(10): 1905-1912.
[5] 宋晓娟, 岳宝增, 闫玉龙, 等. 液体多模态晃动充液航天器姿态机动复合控制[J]. 宇航学报, 2015, 36(7): 819-825.
[6] LEVE F A, NORMAN G. Hybrid sterring logic for
single-gimbal control moment gyroscopes[J]. Journal of Guidance, Control, and Dynamics, 2012, 33(4): 1202-1212.
[7] CUI Mei-yu, XU She-jie. Optimal attitude control of flexible spacecraft with minimum vibration[C]// AIAA Guidance, Navigation, and Control Conference. Toronto: AIAA, 2010: 1-16.
[8] 陈新龙, 杨涤, 翟坤. 某挠性卫星姿态控制系统设计[J]. 哈尔滨工业大学学报, 2008, 40(5): 678-682.
[9] UTKIN V I. Variable structure system with sliding modes[J]. IEEE Trans Autom Control, 1997, 22(2): 212-222.
[10] 李勇, 吴宏鑫. 挠性航天器旋转机动的变结构控制[J]. 航天控制, 1996, 53(1): 19-61.
[11] 管萍, 刘小河, 刘向杰. 挠性卫星的变结构姿态控制[J]. 控制理论与应用, 2007, 24(3): 480-484.
[12] 陕晋军. 挠性空间飞行器的分力合成主动振动抑制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2002: 20-31.
[13] 陕晋军, 刘暾. 挠性结构的分力合成主动振动抑制方法研究[J]. 上海航天, 2001, 18(6): 28-37.
[14] SINGER N C, SEERING W P. Pre-shaping command inputs to reduce system vibration[J]. Journal of Dynamic Systems, Measurement, and Control, 1990, 112(1): 76-82.
[15] CHANG Pyung-hun, PARK Juyi, PARK Joon-yong. Commandless input shaping technique[C]// Proceedings of the American Control Conference. Arlington: [s. n.], 2001: 25-27.
[16] SINIGH T, SINGHOSE W. Tutorial on input shaping/time delay control of maneuvering flexible structures[C]// Proceeding of American Control Conference. Anchorage: [s. n.], 2002: 1717-1731.
[17] TUZCU I. Dynamics and control of flexible aircraft[D]. Blacksburg: Virginia Polytechnic Institute, 2003.
[18] MEIROVITCH L, TUZCU I. Integrated approach to flight dynamics and aeroservoelasticity of whole flexible aircraft-part II: control design: AIAA Guidance, Navigation, and Control Conference and Exhibit[C]// Monterey: 2002.
[19] HU Qing-lei, MA Guang-fu. Vibration suppression of flexible spacecraft during attitude maneuvers[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(2): 377-380.
Research on Input Shaping Attitude Maneuver Method for Large Flexible Satellite Based on PD Control
ZHONG Chao, WU Jing-yu, LU Zhi-jun
(Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)
For some large flexible satellites required fast attitude maneuver, an input shaping attitude maneuver method based on PD control was studied to reduce the effect of flexible vibration on attitude maneuver time in this paper, in which input shaping method was applied to suppress adjunct’s flexible vibration during fast attitude maneuver. The dynamic equation was extended to the state space. The equivalent vibration frequency and damping ratio of the system were solved by computing eigenvalue of the state matrix, so the input shaper was obtained. An input shaping frequency parameters determination method was designed, which was simple and met the requirement in engineering. The PD controller of input shaping was designed, which could realize fast attitude maneuver by Euler axis and reduce adjunct flexible vibration as well. The errors of input shaper were analyzed. The suppress effects of flexible vibration for solar array of some satellite using ZVD, EI, ZVDD and EI-Twohump input shapers were analyzed by simulation. And the attitude error and vibration modal under nominal and deflection of inertia and flexible parameters in maneuvering were also discussed. It found that the method proposed could satisfy the engineering requirement. This method can satisfy engineering requirement, obtain input shaping parameters simply, design approximately the shortest maneuver route, restrain flexible vibration effectively, and complete fast attitude maneuver.
large flexible satellite; input shaping; PD control; attitude maneuver; flexible parameter; attitude control; bandwidth isolation; flexible supression
1006-1630(2017)02-0085-14
2017-02-14;
2017-03-22
钟 超(1984—),男,高级工程师,主要从事航天器控制研究。
V448.2
A
10.19328/j.cnki.1006-1630.2017.02.009
