考虑地球敏感器误差的自主导航方法研究
2017-04-28封天明李涧青高长生荆武兴
封天明,李涧青,高长生,荆武兴
(哈尔滨工业大学 航天学院,黑龙江 哈尔滨150001)
考虑地球敏感器误差的自主导航方法研究
封天明,李涧青,高长生,荆武兴
(哈尔滨工业大学 航天学院,黑龙江 哈尔滨150001)
为减小自主导航过程中地球红外辐射误差及地敏安装误差的影响,以星敏感器和地球敏感器的测量作为导航信息,提出了一种捷联惯导/天文信息组合的自主导航方案。针对地球大气辐射不均匀和地球敏感器安装误差对确定地心矢量的不利影响,建立了地球红外辐射亮度与等效地平高度的关系。利用这一关系,给出了对地球敏感器测量修正的函数关系以及地球敏感器安装误差估计方法。以恒星矢量和地心矢量的星间角距作为量测,采用批处理最小二乘方法对弹道导弹的导航信息进行了估计。仿真结果表明:通过对辐射误差的补偿可大幅提高自主导航的精度,验证了补偿方法的可行性和导航算法的有效性。研究为工程应用中修正地球红外辐射误差提供了一种新思路。
弹道导弹; 自主导航; 组合导航; 地球敏感器; 地球红外辐射; 地敏安装误差; 红外误差补偿; 星敏感器; 最小二乘法
0 引言
弹道导弹是一种远程精确打击武器,其打击精度取决于弹上的导航和制导控制系统。早期的导航方式采用惯性导航技术(INS),但由于惯导器件中的加速度计和陀螺仪存在漂移,导致导航精度随飞行时间而降低,同时单纯提高惯导精度也会增加整个系统的成本,因此纯惯性导航技术已无法满足弹道导弹的高精度打击需求。随着导航技术的发展,出现了以提高导航精度并且降低成本的组合导航技术[1]。GPS作为一种定位方式,首先被考虑用于提高弹道导弹的导航精度,虽然INS/GPS的组合模式效果较好,但受敌对环境的影响,GPS的抗干扰能力较差,因此INS/GPS组合导航技术在实战环境中并不能实现真正的自主导航[2-3]。基于天文信息的导航技术(CNS)具精度高、抗干扰能力强和完全自主等优点,可用于与惯导技术进行互补从而实现组合导航,通过利用不同天体信息可实现不同的INS/CNS组合导航模式[4]。近年来,随着对地磁信息建模的不断完善,基于惯性和地磁组合的导航技术获得了广泛应用。该方法利用了地球磁场信息估计载体位置和姿态[5-6]。文献[7]以磁强计测量值与地磁场模型之差作为量测量,通过混合校正卡尔曼滤波得到导航信息的最优估计。当导弹飞出大气层后,还可采用恒星星光作为测量信息,利用星光折射与大气密度关系可间接测量地平信息,从而实现定位导航[8-9]。此外若将恒星星光直接作为测量信息,可利用星敏感器的高精度特点对导航信息的误差进行修正以提高导航精度[10]。文献[11]考虑在地球敏感器测量精度较低时,将直接敏感地平与间接敏感地平结合,通过互相补偿以提高组合导航的精度。
本文采用星敏感器和地球敏感器组合的天文导航系统提高惯导的导航精度。由于星敏感器属高精度敏感器,组合导航精度取决于地球敏感器的测量与安装精度。地球敏感器通过敏感地球大气红外辐射层确定载体姿态或地心,地球扁率和大气红外辐射强度对地球敏感器的测量结果有较大影响,同时地敏安装误差的存在,也会使测得的地心矢量产生误差。目前,对地球扁率的补偿已有较深入的研究[12]。一般用数值方法得到地平仪扫描角,再通过一阶修正对扫描角进行补偿[13]。或通过对扁率函数的分析得到解析形式的误差数学模型,然后对姿态角进行补偿[14]。但对地球大气红外辐射的不均匀性补偿,目前的研究还较少。地球大气辐射层受纬度、季节和大气密度的影响,大气辐射模型不确定性较大,很难用一种解析方法对其进行补偿。文献[15]用辐射亮度和扫描电压的传递关系建立了扫描电压与姿态误差的关系,通过拟合方法将这种关系近似表示为二次曲线,从而实现了对姿态误差的补偿。文献[16]认为地球敏感器的测量与辐射轮廓密切相关,用相关的大气软件建立了大气辐射与等效地平高度的关系。文献[17]根据这一关系导出了等效地平高度的误差函数,并分别对摆式地平仪和扫描式地平仪的测量结果进行了补偿。地敏安装误差通常会在地面进行静态标定补偿,但由于导弹飞行过程中会存在振动及其它较恶劣的力学环境,使地敏的安装误差在飞行过程中会发生变化,因而有必要进行地敏安装误差的在轨标定,从而在导弹飞行过程中不断地进行安装误差的补偿。
上述文献虽然对载体的姿态进行了补偿,但并未对地心矢量修正进行理论分析且缺少地敏安装误差的在轨标定研究。本文针对地球大气红外辐射不均匀性引起的导航误差进行建模,根据球面几何关系导出了等效地平高度与测量值的修正关系,用这一修正关系对地球敏感器的测量输出进行补偿,同时在这基础上对地面的安装误差进行了在轨标定,以此进行安装误差的补偿,从而修正地心矢量。另综合星敏感器的测量信息,给出了一种基于惯导/星敏/地敏信息的组合导航方案,通过批处理最小二乘方法对惯导的导航信息进行了精确估计。仿真结果验证了组合导航方案的可行性及误差补偿的有效性。
1 地球红外辐射误差模型
1.1 地心矢量确定
扫描式地球敏感器的扫描机构是按一定周期作圆锥运动进行扫描,其扫描视场会形成一个半锥角为γ的圆锥,如图1所示。在测量坐标系OM-XMYMZM中:Hi,Ho分别为敏感器的扫入点和扫出点;E为地心;η为扫描轴OMYM与地垂线的夹角。
假设扫入点时刻为ti,扫出点时刻为to,扫描基准时刻为ts,则定义扫入点至基准的宽度和总弦宽分别为
(1)
式中:Ts为扫描周期。定义姿态偏差角
(2)
根据敏感器测得的扫入扫出时刻,由球面三角形的余弦定理,有
(3)
式中:
(4)
此处:hCO2为地球二氧化碳吸收层高度;R为地心至飞行器的距离;Re为地球半径。由式(2)、(3)可求得βH,η,从而可得地心矢量在测量坐标系中的分量
(5)
这样,由扫描式地球敏感器的测量信息即可确定采样时刻的地心矢量。
1.2 红外误差模型
红外地球敏感器敏感的是地球14~16 μm波段的辐射层亮度。若地球大气的红外辐射是均匀的,则敏感器探测到的地球轮廓是标准的球形,但实际上大气辐射亮度是随纬度和季节而变,因此当敏感器的视场扫入或扫出大气边缘时,辐射亮度会产生不均匀。
根据图2的地平高度定义,辐射亮度的不均匀与地平高度HT的变化有关,因此也正是HT的变化导致了地球敏感器的测量误差。
地球敏感器的测量误差产生过程如图3虚线部分所示。由图3可知:红外辐射误差模型不仅需建立大气辐射亮度L与纬度和环境的关系,而且要建立地平高度与辐射亮度的关系。L是表征辐射能量大小的物理量,即在单位波长宽度范围内,在单位立体角、单位时间内从地表单位面积上辐射出的能量。
为建立辐射亮度与纬度及季节的定量关系,本文采用法国SODERN公司给出的地球红外辐射模型,不同季节地球红外辐射亮度与纬度的关系如图4所示。
由图4可知:在北纬地区,2月和12月,辐射亮度随纬度升高而逐渐降低,5月和9月,则随纬度升高而增加;在南半球情况则完全相反;从南纬20°到北纬20°区域内,辐射亮度波动较小。
为建立辐射亮度与地平高度的定量关系,用美国NASA的CORPS软件计算并给出不同纬度的地平高度与辐射亮度关系,该软件通过大气温度和压强确定地球辐射轮廓[16]。然后根据计算值设计线性函数
HT(L)=
(6)
用式(6)近似辐射亮度与地平高度的关系。由上述近似关系,可得标准大气高度与等效地平高度的误差函数ΔHT=hCO2-HT(L)。
1.3 地球敏感器安装误差模型
地球敏感器安装在导弹弹体上,理想状态下地球敏感器与弹体间有一个标准的安装姿态从而可得标准的测量坐标系OM-XMYMZM。但实际工程中,安装并不能实现完全的准确,同时在导弹飞行过程中,外界复杂的力学环境也使实际的测量坐标系OM-XMeYMeZMe与标准测量坐标系间存在姿态误差角θx,θy,θz,如图5所示。
因安装误差角为小角度,故在实际模型建立过程中,可进行小角度线性化,得安装误差矩阵
(7)
由建立的安装误差矩阵对地面模拟测得的地心矢量进行处理,可得考虑地敏安装误差的地敏测量输出。本文先估计三个安装误差角,再对安装误差进行补偿。
2 地球敏感器红外误差补偿
红外辐射误差的补偿过程如图6所示。由图6可知:只要确定了地平高度与扫入扫出时刻的修正关系,就可对地球敏感器输出的测量值进行修正。
为建立修正关系,先假设扫入点时刻的红外辐射并不均匀,则扫入时刻的视线角
(8)
(9)
由球面三角形余弦定理可得从扫入点至地心中线的弦宽
(10)
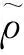
(11)
地球敏感器扫过地球部分的总弦宽
(12)
从扫入点到基准的宽度
(13)
由根据式(10)~(13)可确定弦宽与地平高度的关系为
(14)
用修正后的HD,HS可重新计算地心矢量, 以提高导航精度。由式(9)可知:当误差地平高度不变时,如轨道高度升高,视线角的误差就会减少,而降低敏感器的输出误差。
3 考虑地球敏感器误差的自主导航
3.1 导航原理
弹道导弹在飞出大气层后利用星敏感器观测两颗导航恒星,可得两颗恒星矢量方向S1,S2,利用地球敏感器敏感地球轮廓后得到地心矢量方向E,其导航原理如图7所示。
(15)
上述通过观测计算得到的两个星光角距可作为自主导航的量测方程。结合星历表和导弹的动力学方程及滤波算法即可实现自主导航。
3.2 恒星矢量确定
设星光在星敏感器的CCD面阵投影坐标分别为px,py,光学系统的焦距为fS,则恒星矢量在测量坐标系中的分量可表示为
(16)
星敏感器属于高精度仪器,其精度可达角秒级,但其安装误差对导航精度影响较大。在发射前可对安装位置进行标定。
3.3 基于星间角距的天文导航
自主导航算法采用批处理式的最小二乘方法,选取主动段结束时的初始位置r0、速度v0和地球敏感器安装误差为状态量,有
(17)
观测量的理论计算值可用查询星历表和积分动力学方程得
(18)
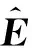
(19)
状态量ξ的猜测误差决定了残差的大小。设通过测量获得N个采样时刻的残差为gi(ξ),建立最小二乘指标
(20)
由最小二乘原理的极值条件,可得迭代估计算法
(21)
式中:
(22)
在当前估值与上一步的差的范数满足一定精度时,停止迭代。一般经迭代4~5次即可停止,则当前的估值ξ*即为得到的精确导航结果。其中:r0,v0可作为惯导系统的积分初值,提高惯导的定位精度;θx,θy,θz可用于补偿地敏安装误差,提高地心矢量的测量精度。
4 仿真校验
为验证地球红外辐射误差补效果和导航算法的有效性,设计标准弹道,导弹飞行时间900s。地球敏感器的γ=40°,Ts=2 s,三轴安装误差均为20″;星敏感器测量误差5″(3σ),用本文方法对加入误差后的速度、位置及地敏安装误差角进行估计。
先在仅考虑地敏安装误差的条件下估计状态量ξ,在估计出地敏安装误差后,对其进行补偿,再次进行导航计算,所得地敏安装误差补偿后的位置和速度误差见表1。由估计误差可知:本文提出的算法能准确估计出地敏的安装误差,表明本文估计算法可行。

表1 仅考虑地敏安装误差的估计误差Tab.1 Estimation error with earth sensor installation error only
在上述仿真的基础上,考虑地球红外辐射误差,用最小二乘导航算法估计主动段关机后的初始状态。用本文红外辐射误差补偿方法对地球红外辐射误差进行补偿,用最小二乘导航算法估计主动段关机后的初始状态,所得误差补偿前后的位置、速度和地敏安装误差的估计误差见表2。由仿真结果可知:不进行地球红外辐射误差补偿,对初始状态的位置估计偏差约1 km,速度估计偏差约2.5 m/s,地敏安装误差角估计偏差约15″;进行地球红外辐射误差修正后,对初值的位置估计偏差减小至约300 m,速度估计偏差减小至约0.3 m/s,地敏安装误差角估计偏差在x、z轴方向很小,在y轴方向则较大,这是由于地敏的y轴为扫描轴,对安装误差的敏感程度较小。上述仿真结果表明:本文提出的地球红外辐射误差补偿及地敏安装误差估计方法,可有效修正辐射误差对地心矢量确定的影响,并估计出地敏的安装误差角,从而提高导航精度。
考虑导航过程中星敏还存在随机测量误差,因此在上述仿真的基础上再加入5″(3σ)的星敏测量误差,进行蒙特卡罗仿真500次,所得结果见表3,初始位置、速度及安装误差等状态估计误差分布如图
8~10所示。由仿真结果可知:均值较小说明地球辐射误差得到了较好的修正,且地敏安装误差也得到较好估计;位置和速度的标准差分别优于100 m,0.2 m/s,导航精度较高。

表2 红外辐射误差补偿前后的估计误差Tab.1 Estimation error before and after infrared radiation compensation

表3 考虑星敏测量误差时红外辐射误差补偿后的估计误差Tab.3 Estimation error after infared radiation compensation with star sensor error
5 结束语
在涉及利用红外辐射测量地心矢量的天文导航领域,对地球扁率的补偿已有较深入的研究,但对地球大气红外辐射的不均匀性补偿,目前的研究还较少。本文针对地球大气红外辐射不均匀性的补偿及相应的地敏安装误差进行了研究。根据地球红外辐射误差模型建立了地球辐射亮度与等效高度的函数关系。由地球敏感器的测量几何原理和安装误差角模型,给出了对地心矢量的修正关系及地敏安装误差角在线标定方法。结合星敏感器的测量信息,用最小二乘算法估计导弹的初始位置、速度和地敏安装误差角。仿真结果表明:本文提出的补偿关系可有效减小红外辐射误差的影响,准确估计出地敏的安装误差角,对初值的位置估计精度优于100 m,速度估计优于0.2 m/s,两个轴的安装误差角估计优于0.3″。因此,本文提出的考虑地球红外辐射的组合导航方案可有效提高弹道导弹的导航精度,并实现地敏安装误差的在轨标定。因星敏感器和地球敏感器的技术已日臻成熟,在工程实践中,利用这两类器件进行组合导航的技术也得到了应用,本文提出的红外误差补偿和地敏安装误差标定方法在实际工程中有较好的应用前景。由于本文对红外辐射误差的修正是通过建立地球红外辐射模型进行的,所建立红外辐射模型精度越高,修正效果就越佳。后续可通过对建模精度的研究,继续提高方法的有效性。
[1] FALL R, DIPIPI M, SLIVINSKY S, et al. Autonomous ballistic missile inertial guidance: a new paradigm for the 21st century[C]// AIAA Guidance, Navigation and Control Conference and Exhibit. [S. l.]: AIAA, 2008: 1-12.
[2] ALI J, FANG J. Realization of an autonomous integrated suite of strapdown astro-inertial navigation systems using unscented particle filtering[J]. Computers & Mathematics with Applications, 2009, 57(2): 169-183.
[3] 王涛, 王雪梅. 一种新的SINS/GPS组合导航建模与滤波[J]. 弹箭与制导学报, 2012, 32(2): 25-28.
[4] HONG D, LIU G B, CHEN H M, et al. Application of missile attitude estimation based on UKF algorithm[J]. Systems Engineering & Electronics, 2010, 32(9): 1987-1990.
[5] NORDLUND P J, GUSTAFSSON F. Marginalized particle filter for accurate and reliable terrain-aided navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(4): 1385-1399.
[6] GUO Cai-fa, CAI Hong, HU Zheng-dong. Nonlinear filtering techniques for geomagnetic navigation[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014, 223(2): 305-320.
[7] 李镇, 王海涌, 靳宇航, 等. 一种弹道导弹捷联惯导/地磁组合导航方法[J]. 中国惯性技术学报, 2015, 23(5): 636-641.
[8] QIAN H, SUN L, CAI J, et al. A novel navigation method used in a ballistic missile[J]. Measurement Science & Technology, 2013, 24(24): 1366-1374.
[9] 宁晓琳, 王龙华, 白鑫贝, 等. 一种星光折射卫星自主导航系统方案设计[J]. 宇航学报, 2012, 33(11): 1601-1610.
[10] 魏新国, 李延鹏, 李健, 等. 多视场星敏感器近地轨道自主定位导航方法[J]. 红外与激光工程, 2014, 43(6): 1812-1817.
[11] 王鹏, 张迎春. 基于星敏感器/红外地平仪的自主导航算法研究[J]. 系统工程与电子技术, 2008, 30(8): 1514-1518.
[12] TEKAWY J A, WANG P, GRAY C W. Scanning horizon sensor attitude correction for Earth oblateness[J]. Journal of Guidance Control & Dynamics, 1996, 19(3): 706-708.
[13] LI J. Simple correction algorithm of scanning horizon sensor measurement for earth oblateness[J]. Journal of Guidance, Control & Dynamics, 1999, 22(1): 187-190.
[14] 周军, 钱勇. 基于地球扁率红外地平仪测量值修正算法研究[J]. 宇航学报, 2003, 24(2): 144-149.
[15] ALEX T K, SHRIVASTAVA S K. On-board correction of systematic error of Earth sensors[J]. IEEE Transactions on Aerospace & Electronic Systems, 1989, 25(3): 373-379.
[16] WARD K A. Modeling of the atmosphere for analysis of horizon sensor performance[J]. Proceedings of SPIE, 1982, 327(12): 67-78.
[17] GONTIN R, WARD K. Horizon sensor accuracy improvement using earth horizon profile phenomenology[J]. Journal of Guidance, Control, and Dynamics, 2013, 10(10): 1495-1502.
Study on Autonomous Navigation with Error of Earth Sensor
FENG Tian-ming, LI Jian-qing, GAO Chang-sheng, JING Wu-xing
(School of Astronautics, Harbin Institute of Technology,Harbin 150001, Heilongjiang, China)
To reduce the impacts made by the earth infrared radiation error and the installation error angles of earth sensor on the precision of autonomous navigation, a strapdown inertial navigation system and celestial navigation system integrated autonomous navigation scheme was proposed using the navigation information obtained from earth sensors and star sensors in this paper. To eliminate the adverse effect caused by the asymmetry of earth infrared radiation and the installation error angles of earth sensor, the relationship between earth infrared radiation brightness and effective horizon height was founded. According to the relationship, a function to correct the measurement of earth sensor was given and the installation error angles of earth sensor were estimated. The angle distance of stars could be calculated, and using this information, the navigation information of ballistic missile was estimated by least square estimation. The simulation results showed that the adverse effect could be greatly mitigated by using the correction scheme. This correction scheme was available and effective. This paper provides a new solution for correcting the earth infrared radiation error in practical applications.
ballistic missile; autonomous navigation; integrated navigation; earth sensor; earth infrared radiation; installation error of earth sensor; earth infrared radiation error correction; star sensor; least square method
1006-1630(2017)02-0112-08
2016-07-20;
2016-11-16
封天明(1994—),男,硕士生,主要从事飞行器动力学,制导与控制研究。
V448.133
A
10.19328/j.cnki.1006-1630.2017.02.012
