基于触力感知的空间非合作目标惯量参数辨识方法研究

楚中毅,马 也,卢 山,侯月阳,王奉文

(1.北京航空航天大学 仪器科学与光电工程学院,北京100191; 2.上海市航天智能控制技术重点实验室,上海 201109; 3.上海航天控制技术研究所,上海 201109)



基于触力感知的空间非合作目标惯量参数辨识方法研究

楚中毅1,马 也1,卢 山2，3,侯月阳2，3,王奉文2，3

(1.北京航空航天大学 仪器科学与光电工程学院,北京100191; 2.上海市航天智能控制技术重点实验室,上海 201109; 3.上海航天控制技术研究所,上海 201109)

因空间机械臂系统内部存在较强的动力学与运动学耦合关系，为防止捕获操作对系统的姿态和轨迹产生影响，需对捕获的空间非合作目标的惯量参数进行精确辨识，针对传统的辨识研究仅考虑辨识的基本原理，忽略了实际辨识过程中存在的辨识误差等重要问题，提出了一种新颖的基于触力信息的空间非合作目标惯量参数完整辨识方法。先对辨识过程中存在的各种误差及其对辨识结果影响进行了理论推导，在此基础上提出了一种包含末端触力信息及末端执行器力、力矩信息的改进辨识方程，削弱辨识过程中误差的累积效应及其对辨识结果的影响。此外，考虑量测误差中包含复杂的噪声信息，提出了递推最小二乘法-仿射投影符号算法(RLS-APSA)混合算法，并基于此算法解算辨识方程，以确保辨识结果的稳定性。为验证所提辨识方法的有效性，构造了多自由度空间机械臂系统模型，用Adams-Matlab联合仿真平台进行相应的仿真实验，实验结果证实了所提辨识方法的有效性。

空间非合作目标； 惯量参数； 触力信息； 递推最小二乘法-仿射投影符号算法； 参数辨识； 辨识误差； 空间机械臂； 触力感知

0 引言

在轨服务是航天技术中一个极为重要和极具竞争力的领域，未来将实施频繁的航天活动计划。基于无人参与的空间在轨服务，不仅降低了航天员在轨操作的风险，而且降低了运营成本，因此在太空捕获、对接、修复和维护活动中将发挥不可或缺的作用[1]。航天器通过固连于其本体的机械臂捕获空间非合作目标。当航天器系统处于自由漂浮状态时，因其内部存在较强的动力学、运动学耦合关系，且非合作目标的惯量特性未知，因此捕获过程会对航天器原有的姿态和轨迹产生影响[2]。另外，由于捕获目标的属性未知，这对航天器自身控制系统的控制效果及精度提出了严峻考验。为实现精确控制，确保航天器正常工作，需先获取非合作目标的惯量参数，如质量、质心和惯性张量等，进而实施明确的太空操作任务[3]。

为辨识空间非合作目标的惯量参数，应先获得非合作目标相对惯性坐标系的运动特性。考虑太空中系统强耦合特性和空间参数辨识的非线性特性，基于传统的地面固定基座的目标辨识方案会失效[4-5]。因此，文献[6]提出了一个基于后捕获阶段系统动量守恒方程构造的空间未知对象参数辨识方案(动量守恒方程(MC)和运动方程(EM))[1]。因航天器系统处于自由漂浮状态，且不受外力作用，因此满足线动量和角动量守恒。文献[7]考虑了太空微重力梯度效应，用MC方法对空间非合作目标惯量参数进行辨识。文献[8]通过在航天器本体上安置加速度计以检测和预估系统的运动学信息，实现了对捕获目标惯量参数的辨识。文献[9]通过改变航天器系统的惯性分布，用蒙特卡罗方法确定了航天器的性质。文献[10]在MC方法的基础上提出了自适应无反作用的机械臂路径规划及捕获目标的惯量参数辨识。文献[11]提出了一种基于后捕获阶段的非合作目标的重构控制策略，并利用空间机械臂和捕获对象的未知属性进行重构。基于视觉的空间目标辨识方法通过安装在末端的摄像头采集捕获物体的运动信息，实现对目标惯量参数的估计[12-13]。文献[14]提出了利用绳系系统对非合作目标进行捕获并辨识的过程，而基于绳系捕获后续的协调控制策略则在文献[15]中有所体现。综上，空间目标的惯量参数辨识方法可分为两类：基于运动学特性(线、角速度)的动量方程列写求解(MC)，以及基于系统动力学特性的牛顿欧拉、拉格朗日方程列写求解(EM)。这两类方法有一个相同的性质，即均是构建一个线性辨识方程估计目标完整的惯量参数。MC方法只需速度系统，而不包含加速度信息，减小了信息量测噪声的介入对辨识精度的影响，因此成为目前主要的惯量参数辨识方法。

通常，线性辨识方程的解即为非合作目标的惯量参数，因而线性方程的系数决定了解的精度，即惯量参数的辨识精度[16]。通过研究方程的系数矩阵，发现主导其解精度的因素主要为非合作目标的运动学信息，以及系统中航天器本体、机械臂的惯量参数。从已有的研究可发现，这两个重要因素均被认定为理想获得，并未考虑系数中存在的误差[6]。事实上，由于不可避免的外部干扰和内部因素，量测信息包含的量测误差不可消除，而这些误差会直接影响惯量参数的辨识精度。此外，因太空操作导致燃料消耗，故航天器本体的惯量参数也不是常值，需实时估计，而估计过程中同样伴随有估计误差[7-9]。因此，认定运动学信息的量测误差以及系统惯量参数的估计误差是影响捕获目标惯量参数辨识的主要因素。文献[8]通过误差界估计方法阐述了航天器本体惯量参数的误差估计过程。然而，一直缺乏有关估计、量测误差对捕获的空间非合作目标定量影响的研究。

本文在原有理论的基础上，研究了量测、估计误差及其在运算过程中的累积效应对惯量参数辨识的影响，通过分析得出量测误差的累积效应是影响非合作目标惯量参数辨识精度的主要原因。为减弱量测误差的累积效应，采用基于末端触力与力、力矩传感信息的改进的辨识方程，以提高参数的辨识精度。由于末端触力信息以及末端力、力矩直接反映了捕获目标的受力状态，无需通过间接的理论推导就可实现量测信息的估计，因而减小了量测误差的累积过程。本文通过动量定理，根据末端目标的冲量变化量恒等于动量变化量改进传统MC方法的辨识方程。考虑接触力的测量，以及末端力、力矩的量测手段已日趋完善，本文提出了一种基于末端触力信息以及末端力、力矩信息的空间非合作目标惯量参数辨识方法，通过改进的辨识方程减弱误差累积，提高惯量参数的辨识精度[17-19]。本文研究的创新点主要有以下3个：一是量测、估计误差对辨识精度的定量分析；二是提出了结合末端触力和力、力矩信息的改进的辨识方程；三是提出RLS-APSA混合算法解算改进的辨识方程，以确保辨识过程的稳定。本文根据辨识的基本理论，包括一个N自由度空间机械臂系统的运动学(多自由度)和传统辨识方程，分析了运动量测误差对传统辨识方程辨识精度的影响；通过引入末端力信息修改传统辨识方程，减小误差累积效应，进而提高参数精度；基于复杂的噪声条件提出了RLS-APSA混合算法，以确保辨识过程的稳定性。用构造的Adams-Matlab联合仿真平台进行仿真实验，以验证本文所提理论的有效性。

1 动态量测误差分析

1.1 辨识基本理论

刚性空间机械臂系统由航天器本体、机械臂和捕获的空间非合作目标组成，如图1所示。系统处于自由漂浮状态，且不受外力，故系统满足动量守恒条件[6,10]。图1中：I，B，i，U分别为惯性系、航天器本体系、关节坐标系和末端系；pB(p0)，pi，pU(pn+1)分别为对应参考点的位置向量在惯性系中的表示；rB(p0)，ri，rU分别为系统各部分质心位置在惯性系中的表示；ωB(ω0)，ωi，ωU分别为航天器本体角速度、关节角速度，以及末端角速度在惯性系中的表示；θi为对应关节角度在惯性系中的辨识。因此，由文献[6，16]存在以下几何关系

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

本文考虑的是后捕获阶段空间机械臂系统的运动学，假定该系统为刚性机构，且不考虑使用反作用轮和其它动量交换装置，末端的捕获目标与末端操作器固连于一体。由文献[6，16]可知整个空间机器臂系统的线、角动量均为零，即

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

式(12)可分解为

(18)

(19)

由式(18)、(19)可得两个重要结论。

a)为确保线性辨识方程的系数矩阵式(12)为非奇异矩阵，保证完整的参数辨识条件，须满足空间三维正交方向上均存在运动学信息这一条件，即惯量参数(质量、质心和惯量)完整辨识的充分必要条件与目标现有的平移、旋转运动信息在3个正交方向上的分量有关，故在后捕获阶可通过驱动不同方向的关节运动以保证完整的辨识条件[6，10]。

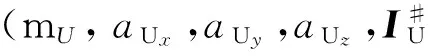
(20)

(21)

上述分解过程为分步辨识过程，如图2所示，目的是提高惯量参数辨别的精度。

1.2 运动学量测误差对辨识精度的影响

由式(20)、(21)可知：系数(ωU)，U，LK-(PK)·aU决定了参数的辨识精度。由式(4)～(9)可知U可通过运动学信息i推导得到。由式(13)、(14)可知：PK，LK依赖于机械臂和航天器本体的惯量参数与运动学参数，而这些运动学参数均可通过i及以上运动学等式推导出。故运动学量测信息i及航天器、机械臂惯量参数的误差决定了非合作目标参数(mU，aU，IU)的辨识精度。

为独立分析运动学量测误差对辨识结果的影响，首先假定已精确知道系统的惯量参数，即惯量估计误差为零。

在包含量测噪声的条件下，式(20)、(21)转化为

(22)

(23)

式中：

(24)

(25)

(26)

(27)

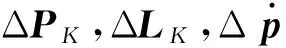
(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

由式(13)、(14)可得

(37)

(38)

将式(28)～(36)代入式(37)、(38)，可得

(39)

(40)

对比式(35)、(36)，(39)、(40)，(24)～(27)，可得

(41)

(42)

(43)

(44)

(45)

(46)

(47)

(48)

(49)

2 包含末端触力及末端末端力、力矩信息的惯量参数辨识

2.1 改进的惯量参数辨识方程

实际上，fU，fn，nn可通过触觉传感器和力、力矩传感器测得[20-21]。其余力学信息的推导过程为

(50)

(51)

(52)

(53)

通过上述推导过程可获得改进后的参数辨识方程。

系统的动量可分解为

(54)

(55)

对系统动量守恒方程及方程求导，可得

(56)

(57)

由动量定理可得

(58)

(59)

合并式(56)、(57)和(58)、(59)可得

(60)

(61)

基于增量式的MC方程(避免求解系统初始动量)(文献[9-10])，式(22)、(23)可替换为

(62)

(63)

合并式(61)～(63)，可得改进后的辨识方程

(64)

(65)

根据式(50)～(53)，式(64)、(65)被替换为

[(δ(ωU+ΔωU))×]·aU=

[(δ(ωU+ΔωU))×]·aU

(66)

(bn+aU)×(fU+ΔfU))dt-IE(ωU+ΔωU)=

IE·ωU-IE·ΔωU=

(67)

故获得的改进辨识方程系数的误差项

(68)

(69)

现考虑以下两个实际情况。

a)以上部分考虑的误差分析均是在惯性坐标系中表示的向量和矩阵，目的是简化分析过程。但实际上，所测得的接触力和末端执行器的力、力矩的数据总是表示在末端坐标系U，n中。故在实际计算中需转换矩阵的摄入，这就要考虑航天器的姿态角信息)及所有关节的驱动角度i信息，而这一过程又会不可避免地引入误差的累积，有时这种累积过程不显著。因此，旋转矩阵的误差累积对辨识过程影响的减小仍是一个亟待解决的问题。

b)式(64)、(65)的积分精度与实际信号的采集周期有关。实际上，连续的量测信号f，n是不存在的。故实际中的积分运算可通过一段时间内力、力矩信息的历史曲线获得，而积分区段和实际信号的采样频率决定了积分项的精度。积分区段选取过长或过短都会降低积分项的精度，选取一个合适的时间比例γ(采样率)是必要的。有

(70)

式中：τf, n为末端力、力矩的实际采样周期。

2.2 混合辨识算法RLS-APSA

由式(64)、(65)可构造线性方程

(71)

(72)

式中：

fU-aU×fU)dt-IEωU

上述线性方程的简化形式为

(73)

式中：θ为非合作目标惯量参数向量；A，b分别为对应的系数矩阵和向量。

在式(71)、(72)中，奇异线性方程需通过构造正定或超定方程组，并通过采集多组系数矩阵(A，b)求解，故可用线性回归算法和自适应滤波算法求解改进后的辨识方程式(73)。传统的辨识方法使用最小二乘法(LS)和递推最小二乘(RLS)算法得到对应的辨识结果，但LS，RLS不能有效解决实际中存在的有色噪声或强烈的尖峰脉冲噪声等问题。为此，本文提出一种混合算法，它包含RLS和仿射投影符号算法(APSA)两部分[22-24]。其中：RLS主要保证收敛速率和减小测量数据的相关度，且可迅速获得辨识参数的近似结果；APSA具免疫有色噪声和脉冲噪声的功能，且计算复杂度较低，只能维持缓慢的收敛速率[25-26]。RLS，APSA的标准回归形式为

(74)

(75)

式(74)中，λ可调整收敛速率，并削弱历史数据对当前数据的影响[25]。式(75)中，μ，ε(取小正数)调整APSA的收敛速率。

为合并两种算法，需一个切换这两种算法的切换机制。根据文献[24]，切换机制设计为

(76)

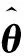
(77)

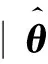
3 数值仿真

为验证本文提出的辨识方法的有效性，通过动力学标准建模软件ADAMS建立3，7自由度的简化空间机械臂系统动力学模型如图4所示。两种自由度空间机械臂模型的几何惯性参数分别见表1、2，参数均为各自本体系中的表示。系统保持零初始状态，即机械臂系统各部分的初始线、角速度均为零。为保证参数完整可辨识以及不同正交方向的关节同时被驱动以产生三维空间的运动形式，驱动信号均采用余弦函数，驱动时间为100 s，且系统处于后捕获阶段，见表3。辨识过程由Adams-Matlab联合仿真平台实现，设仿真采样周期τ=0.005 s，积分

时间δt=0.1 s，γ=0.05。

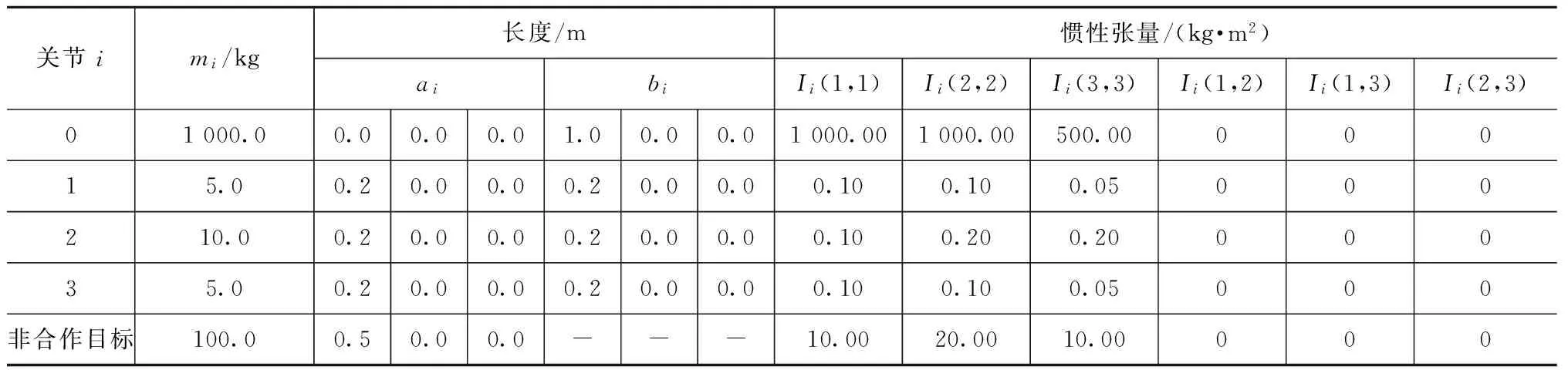
表1 3自由度空间机械臂模型的几何惯量参数Tab.1 Geometric and inertial parameters of space robot system model with 3-DOF manipulator

表2 7自由度空间机械臂模型的几何惯量参数Tab.2 Geometric and inertial parameters of space robot system model with 7-DOF manipulator

表3 关节驱动信号Tab.3 Actuating signals of joints

(78)

v2=x2(t)+0.01x2(t-0.1)

(79)

式中：x1(t)，x2(t)为零均值、标准差1%信号幅值的随机信号。

考虑太空操作中的燃料消耗，设置航天器惯量参数的估计误差为理论值的5%[8]。

由式(62)～(65)可知：常规RLS算法和RLS-APSA混合算法的理想参数设置在辨识过程中起决定作用，因此在仿真中使用理想参数，见表5。

为对比改进辨识方程与常规辨识方程的辨识效果，通过简化的3自由度空间机械臂系统模型进行相应的仿真实验。为验证改进辨识方程辨识精度的优势，分别采用改进辨识方程和常规辨识方程通过同一辨识算法进行仿真实验，参数设置见表5。另外，为验证所提出的RLS-APSA混合算法的有效性，在改进辨识方程的辨识条件下用常规RLS算法和RLS-APSA混合算法求解。辨识过程中量测信息的量测噪声添加见式(78)、(79)和表4。

3自由度空间机械臂改进辨识方程与常规辨识

方程的参数mU，aUx，aUy，aUz，IUxx，IUyy，IUzz，IUxy，IUXz，IUyz的辨识结果分别如图5～8所示(各图的图例相同)。由图5～8可知：在两种辨识算法(常规RLS算法和RLS-APSA混合算法)的解算下，与常规辨识方程相比，改进辨识方程求得的辨识参数有极大的精度优势，只有aUy，aUz两个参数的优势不明显。另外，在相同的仿真条件下，RLS-APSA混合算法较常规RLS算法在包含混合量测噪声(高斯白噪声、高斯有色噪声、脉冲噪声)的条件下呈现出辨识结果的稳定性，在辨识过程的初始阶段，辨识结果出现一定的波动(RLS)，波动到一定程度辨识结果趋于稳定，从波动到稳定的转折主要是ρ1发挥了算法切换的作用。

表4 脉冲噪声v3Tab.4 Impulsive noises v3 of signal magnitude

表5 RLS，RLS-APSA算法理想参数设置Tab.5 Ideal parameter settings for RLS and RLS-APSA algorithms

3自由度空间机械臂改进辨识方程与常规辨识方程在90～100 s的参数辨识均值及误差见表6。由表6可知：使用RLS-APSA混合算法时，改进辨识方法的精度较常规辨识方法有较大提升。以上结果证明了基于包含末端力信息的参数辨识方法对辨识结果精度的提升作用。

事实上，末端触力和末端力、力矩的量测精度在辨识过程中对辨识结果起基础性作用。为体现不同量测精度对辨识结果的影响，定义末端触力信息和末端力、力矩信息在仿真中所施加的不同量测噪声，见表7。仿真所得不同噪声等级下3自由度空间机械臂改进辨识方程参数mU，aUx，aUy，aUz，IUxx，IUyy，IUzz，IUxy，IUxz，IUyz的辨识结果分别如图9～12所示(各图图例相同)，辨识结果见表8。由图9～12和表8可知：改进辨识方程相比常规辨识方程仍显示出精度优势，尽管末端触力和力、力矩信息选取了不同的量测噪声，且随末端力信息量测精度的提升，参数的辨识精度略有提高。

类似地， 7自由度空间机械臂系统改进辨识方程与常规辨识方程，以及在不同噪声等级下改进辨识方程的参数mU，aUx，aUy，aUz，IUxx，IUyy，IUzz，

表6 3自由度空间机械臂在90～100 s时改进辨识方程与常规辨识方程的参数辨识均值及误差Tab.6 Mean values and errors identification parameters of modified and conventional identification equation in 90～100 s for 3-DOF manipulator

表7 高斯白噪声等级Tab.7 Rank of Gauss white noise

IUxy，IUxz，IUyz的辨识结果分别如图13～20所示(图13～16、图17～20图例分别相同)，辨识结果对比分别见表9、10。

表8 3自由度空间机械臂不同等级噪声下改进辨识方程在70～80 s的参数辨识均值及误差

Tab.8 Mean values and errors identification parameters of modified identification equation via various ranks of measured noises in 70～80 s for 3-DOF manipulator

惯性参数标称值改进辨识方程噪声A噪声B噪声C均值误差/%均值误差/%均值误差/%传统辨识方程均值误差/%mU/kg100.00100.940.94101.231.23102.342.34107.987.98aUx/m0.500.498-0.40.497-0.60.494-1.20.482-3.6aUy/m0.000.0017-0.0018-0.002-0.006-aUz/m0.000.00005--0.00007--0.00009-0.0035-IUxx/(kg·m2)10.0010.020.210.030.310.060.611.818IUyy/(kg·m2)0.000.12-0.13-0.15-0.2-IUzz/(kg·m2)0.000.04-0.6-0.9--0.18-IUxz/(kg·m2)20.0020.2120.31.520.73.523.816IUxz/(kg·m2)0.00-0.21--0.27--0.72-1.3-IUyz/(kg·m2)10.0010.1110.151.510.353.512.121

因此可得出结论：机械臂末端触力和末端执行器力、力矩信息的引入显著降低了传统辨识方程中量测误差和惯量参数估计误差的累积效应，进而提高了末端捕获的非合作目标惯量参数的辨识精度，且提出的RLS-APSA混合算法在不同量测噪声下依然能保证辨识过程的稳定。

惯量参数标称值改进辨识方程常规辨识方程RLSRLS-APSARLSRLS-APSA均值误差/%均值误差/%均值误差/%均值误差/%mU/kg500.00--510.122.02--519.723.94aUx/m0.00---0.002---0.026-aUy/m-0.25---0.2520.8---0.2916aUz/m0.00--0.005---0.023-IUxx/(kg·m2)100.00--101.121.12--162.8162.81IUyy/(kg·m2)0.00---0.52----24.58-IUzz/(kg·m2)0.00---5.71----26.9-IUxz/(kg·m2)200.00--201.330.67--222.1211.06IUxz/(kg·m2)0.00--3.28---6.45-IUyz/(kg·m2)200.00--200.940.47--145.37-27.32

4 结论

本文提出了一种通过引入末端触力信息，以及末端力、力矩信息的非合作目标惯量参数辨识方法。先对非合作目标惯量参数的完整辨识条件进行了理论分析，在此基础上提出分步辨识方法，降低常规辨识方程的耦合程度；通过分析常规辨识方程中的量测误差和估计误差的累计效应，提出了引入末端触力及末端力、力矩信息的改进辨识方程，以降低误差累积效应，提高惯量参数的辨识精度。同时，采用RLS-APSA混合算法解算改进辨识方程，克服了不同的噪声干扰，保证了辨识过程的稳定。数值仿真结果验证了本文所提理论的有效性，说明该方法能有效保证执行太空任务，并防止任务失败。

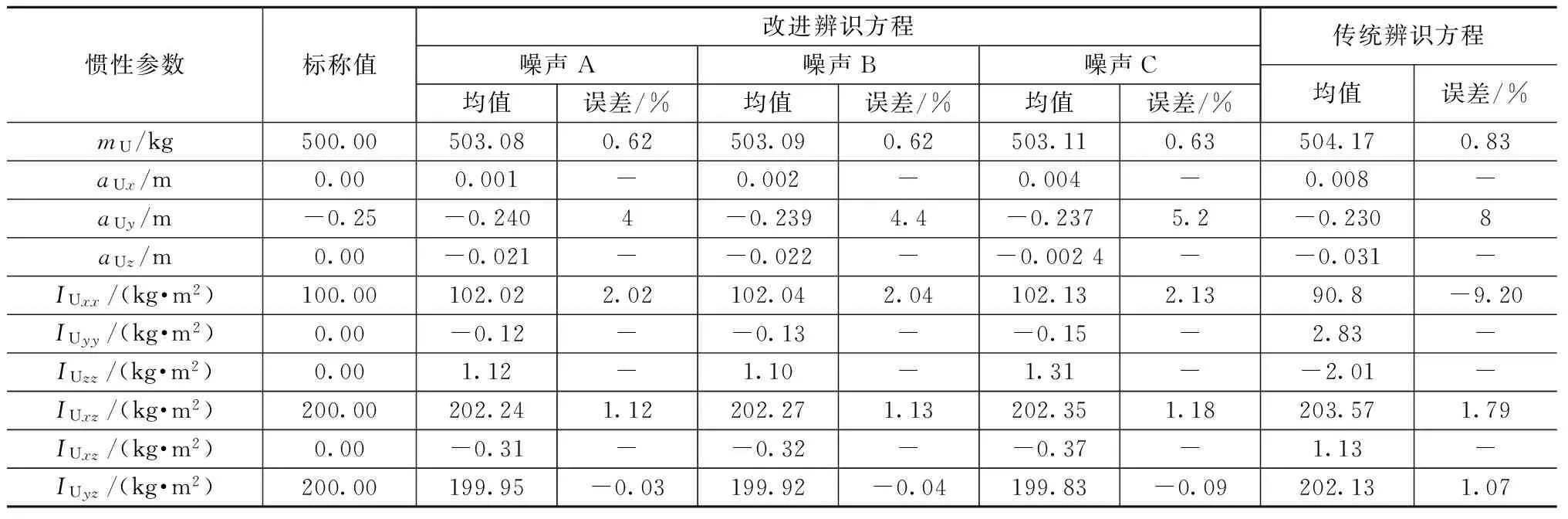
惯性参数标称值改进辨识方程噪声A噪声B噪声C均值误差/%均值误差/%均值误差/%传统辨识方程均值误差/%mU/kg500.00503.080.62503.090.62503.110.63504.170.83aUx/m0.000.001-0.002-0.004-0.008-aUy/m-0.25-0.2404-0.2394.4-0.2375.2-0.2308aUz/m0.00-0.021--0.022--0.0024--0.031-IUxx/(kg·m2)100.00102.022.02102.042.04102.132.1390.8-9.20IUyy/(kg·m2)0.00-0.12--0.13--0.15-2.83-IUzz/(kg·m2)0.001.12-1.10-1.31--2.01-IUxz/(kg·m2)200.00202.241.12202.271.13202.351.18203.571.79IUxz/(kg·m2)0.00-0.31--0.32--0.37-1.13-IUyz/(kg·m2)200.00199.95-0.03199.92-0.04199.83-0.09202.131.07

[1] FLORES-ABAD A, MA O, PHAM K, et al. A review of space robotics technologies for on-orbit servicing[J]. Progress in Aerospace Sciences, 2014, 68(8): 1-26.

[2] DUBOWSKY S, PAPADOPOULOS E. The kinematics, dynamics, and control of free-flying and free-floating space robotic systems[J]. IEEE Transactions on Robotics and Automation, 1993, 9(5): 531-543.

[3] FELICETTI L, GASBARRI P, PISCULLI A, et al. Design of robotic manipulators for orbit removal of spent launchers’ stages[J]. Acta Astronautica, 2016, 119: 18-130.

[4] SCHEDLINSKI C, LINK M. A survey of current inertia parameter identification methods[J]. Mechanical Systems and Signal Processing, 2001, 15(1): 189-211.

[5] YU Y, ARIMA T, TSUJIO S. Inertia parameters estimation of planar object on robot pushing operation[J]. International Journal of Information Acquisition, 2009, 6(4): 239-247.

[6] MUROTSU Y, SENDA K, OZAKI M. Parameter identification of unknown object handled by free-flying space robot[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(3): 488-494.

[7] YOSHIDA K, ABIKO S. Inertia parameter identification for a free-flying space robot[C]// AIAA Guidance, Navigation, and Control Conference and Exhibit. Monterey: AIAA, 2002: 2388-2394.

[8] LAMPARIELLO R, HIRZINGER G. Modeling and experimental design for the on-orbit inertial parameter identification of free-flying space robots[C]// Proceedings of IDETC/CIE, ASME 2005 International Design Engineering Technical Conferences.[S.l.]: [s. n.], 2005: 881-890.

[9] MA O, DANG H. On-orbit identification of inertia properties of spacecraft using a robotic arm[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1761-1771.

[10] NGUYEN-HUYNH T C, SHARF I. Adaptive reactionless motion and parameter identification[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 404-414.

[11] HUANG P F, WANG M, MENG Z J, et al. Attitude takeover control for post-capture of target spacecraft using space robot[J]. Aerospace Science and Technology, 2016, 51: 171-180.

[12] AGHILI F, PARSA K. Motion and parameter estimation of space objects using laser-vision data[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 537-549.

[13] TWEDDLE B E, SAENZ-OTEREO A, LEONARD J J, et al. Factor graph modelling of rigid-body dynamics for localization, mapping, and parameter estimation of a spinning object in space[J]. Journal of Field Robotics, 2015, 32(6): 897-933.

[14] ZHANG F, SHARF I, MISRA A, et al. On-line estimation of inertia parameters of space debris for its tether-assisted removal[J]. Acta Astronautica, 2015, 107: 150-162.

[15] WANG D K, HUANG P F, CAI J, et al. Coordinated control of tethered space robot using mobile tether attachment point in approaching phase[J]. Advances in Space Research, 2014, 54(6): 1077-1091.

[16] SUN J, MA Y, ZHANG S J, et al. Ada line network based identification method of inertial parameters for space uncooperative targets[J]. Acta Aeronautica Et Astronautica Sinica, 2016, 37(9): 2799-2808. DOI: 10.7527/S1000-6893.2015.0349.

[17] GIRAO P S, RAMOS P M P, POSTOLACHE O, et al. Tactile sensors for robotic applications[J]. Measurement, 2013, 46: 1257-1271.

[18] HIRZINGER G, BRUNNER B, DIETRICH J. Sensor-based space robotics-ROTEX and its telerobotics features[J]. IEEE Transactions on Robotics and Automation, 1993, 9(5): 649-662.

[19] NAKAMOTO H, KOBAYASHI F, IMAMURA N, et al. Universal robot hand equipped with tactile and joint torque sensors: development and experiment on stiffness control and object recognition[J]. Journal of Systemic, Cybernetics and Informatics, 2007, 5(2): 79-84.

[20] JUNG Y, LEE D G, PARK J, et al. Piezoresistive tactile sensor discriminating multidirectional forces[J]. Sensors, 2015, 15: 25463-25473.

[21] GOEGER D, ECKER N, WOERN H. Tactile sensor and algorithm to detect slip in robot grasping processes[C]// Proceedings of the 2008 IEEE, International Conference on Robotics and Biomimetics. Bangkok, [S. l.]: [s. n.], 2009: 1480-1485.

[22] HUANG H, FRNTI P, HUANG D, et al. Cascaded RLS-LMS prediction in MPEG-4 lossless audio coding[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2008, 16 (3): 554-562.

[23] YSEBAERT G, VANBLEU K, CUYPERS G, et al. Combined RLS-LMS initialization for per tone equalizers in DMT-Receivers[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 916-1926.

[24] VEMURI S H K, PANAHI I. Hybrid RLS-NLMS algorithm for real-time remote active noise control using directional ultrasonic loudspeaker[C]// IECON 2014-40th Annual Conference of the IEEE, Industrial Electronics Society. Dallas: [s. n.], 2014: 2418-2424.

[25] EWEDA E, MACCHI O. Convergence of the RLS and LMS adaptive filters[J]. IEEE Transactions on Circuits and Systems, 1987, 34(7): 799-803.

[26] SHAO T, ZHENG Y R, BENESTY J. An affine projection sign algorithm robust against impulsive interferences[J]. IEEE Signal Processing Letters, 2010, 17(4): 327-330.

Contact-Force Measurement Based Inertial Parameter Identification Method for a Space Non-Cooperative Target

CHU Zhong-yi1, MA Ye1, LU Shan2， 3, HOU Yue-yang2， 3, WANG Feng-wen2， 3

(1. School of Instrument Science and Opto-Electronics, Beihang University, Beijing 100191, China；2. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;3. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

A novel contact-force information based inertial parameter identification method for a space non-cooperative target was presented because of strong dynamic and kinematic coupling existing in space robot system, while the inertial parameter identification of the space non-cooperative target was essential for the ideal control strategy based on changes in the attitude and trajectory of the space robot via capturing operations and conventional studies would merely refer to the principle and theory of identification, and ignore identification error in practical identification process. To solve this issue, all kinds of errors in identification and the effect of these errors on identification results were firstly illustrated, and a modified identification equation incorporating end contact-force information, as well as force and torque information of end-effector, were proposed to weaken the accumulation of errors and the effect of errors on identification results. Furthermore, considering complex noise information in measurement error, a hybrid immune algorithm, recursive least squares and affine projection sign algorithm (RLS-APSA), was employed to decode the modified identification equation to ensure a stable identification property. To verify the validity of the proposed identification method, the co-simulation of Adams-Matlab was implemented by space robot system models with multi-degree of freedom. The numerical results show the proposed method is effective.

space non-cooperative object; inertial parameter; contact-force information; RLS-APSA; parameter identification; identification error; space robot system; contact-force measurement

1006-1630(2017)02-0030-17

2017-01-24；

2017-03-29

上海航天科技创新基金资助(SAST2015075)

楚中毅(1977—)，男，教授,主要从事空间智能操控技术、航天器动力学与控制技术的研究。

V448.22

A

10.19328/j.cnki.1006-1630.2017.02.002