开关寿命连续型且部件修复非新的温贮备可修系统
2017-04-27张民悦连爱玲
张民悦, 连爱玲
(兰州理工大学理学院, 兰州730050)
开关寿命连续型且部件修复非新的温贮备可修系统
张民悦, 连爱玲
(兰州理工大学理学院, 兰州730050)
主要讨论在开关不完全可靠、部件修复非新且修理工可多重休假的情况下,通过假定部件的工作寿命、贮备寿命、转换开关的寿命以及部件1的修理时间均服从指数分布,修理工的休假时间、开关和部件2的修理时间均服从一般连续型分布,分析讨论系统可能出现的状态,利用补充变量法将其扩充为广义Markov过程,再建立状态微分方程,并应用Laplace变换及其反演,得到系统的可用度、故障频度、系统等待修理的概率与修理工休假的概率、可靠度及首次故障前平均时间等重要可靠性指标。最后给出了在开关完全可靠的情形下,即修理工多重休假且部件修复非新,系统的稳态指标。
开关寿命连续型;修复非新;修理工多重休假;补充变量法;广义Markov过程;Laplace变换
引言
温贮备系统是可靠性模型中比较重要的模型之一[1-2],此类模型从实际出发,考虑了部件在贮备过程中也会发生失效的情况。文献[3]研究了2个不同部件温贮备系统的几何模型。文献[4-5]研究了具有优先权的温贮备系统。以上文献均未考虑修理工休假的情况,在实际中,修理工休假对系统有重要的作用,文献[6-8]把修理工休假的情况引入到温贮备系统中,研究了修理工休假情况下系统的可靠性。在贮备系统中,贮备部件通常需要转换开关来转换,文献[9]分析了开关不完全可靠的情况下系统的可靠性。文献[10]考虑了开关不完全可靠和修理工多重休假两种因素下的温贮备系统可靠性。
上述文献都是假定在部件能够修复如新的情况下研究的,但在实际生活中,失效部件随着修理次数的增多,其使用寿命会越来越短,故障修理时间会越来越长。文献[11-12]是修理工在不同休假情况下部件不能修复如新的温贮备系统。文献[13-14]研究的是修复非新的并联系统。
本文在以上文献的基础上对部件不能修复如新的温贮备可修系统进行延伸,综合考虑了修理工休假、开关不完全可靠以及部件修复非新等因素下,应用补充变量法和广义Markov过程法得到系统的主要可靠性指标。
1模型假定
根据已有文献对系统模型做如下假定:
(1) 系统由两个不同型部件、一个不完全可靠的转换开关和一个多重休假的修理工组成。初始时刻,系统良好,部件1工作,部件2温贮备,修理工休假。
(2) 部件1比部件2有优先使用权和修理权,修理工采用多重休假的策略。
(3) 定义系统的第n次循环是从部件第n-1次修理完成到第n次修理完成之间的时间间隔,n=1,2,3,…。


W(t)=1-exp{-βt},β>0

开关的寿命和修理时间分别记为L,GK,其分布分别为:
L(t)=1-exp{-pt},p>0
修理工每次休假时间H(t)分布函数为:
(5)随机变量之间均相互独立。
2系统的状态方程及其求解
令Nn(t)表示系统在时刻t时所处的状态,则系统可能的状态如下:
0=(a,b,c,e),1=(a,b,d,e),2=(a,g,c,e)
3=(a,g,d,e),4=(f,h,c,e),5=(f,h,d,e)
6=(a,b,k),7=(a,g,k),8=(f,h,k),9=(i,h,c)
10=(i,h,d),11=(a,j,c),12=(a,j,d)
13=(f,g,c,e),14=(f,g,d,e),15=(f,b,d,e)
16=(f,b,k),17=(f,g,k),18=(i,g,c)
19=(i,g,d),20=(f,j,c),21=(f,j,d)
其中:a表示部件1工作,b表示部件2贮备,c表示开关正常,d表示开关失效,e表示修理工休假,f表示部件1失效,g表示部件2失效,h表示部件2工作,i表示部件1修理,j表示部件2修理,k表示开关修理。显然,系统的状态空间为:
E={0,1,2,3,4,5,6,7,8,9,10,11,12,13, 14,15,16,17,18,19,20,21}
系统的工作状态F={0,1,2,3,4,5,6,7,8,9,10,11,12},系统的故障状态W={13,14,15,16,17,18,19,20,21},此模型过程不是Markov过程,引入补充变量:X(n)(t)表示在时刻t时系统在第n次循环中修理工已用去的休假时间,Y(n)(t)表示在时刻t时系统在第n次循环中正在被修理的部件已用去的修理时间,Z(n)(t)表示在时刻t时系统在第n次循环中开关已用去的修理时间,则{N(n)(t),X(n)(t),Y(n)(t),Z(n)(t)}构成一个广义Markov过程,系统在时刻t的状态概率定义为:
Pi(t,x)dx=P{N(n)(t)=i,x≤X(n)(t) i=0,1,2,3,4,5,13,14,15 Pj(t,y)dy=P{N(n)(t)=j,y≤Y(n)(t) j=9,10,11,12,18,19,20,21 Pk(t,z)dz=P{N(n)(t)=k,z≤Z(n)(t) k=6,7,8,16,17 为了计算的方便,引入以下变换: 拉普拉斯变换: 拉普拉斯司梯阶变换: 由偏微分方程理论可得系统各状态概率微分方程组: pP2(t,x)+βP1(t,x) ∂P4(t,x) an-1λP3(t,x)+∂P5(t,x) βP16(t,z)+∂P8(t,z) an-1λP12(t,y) 初始条件:P0(0,0)=1,其余为0,边界条件: Pi(t,0)=0,i=1,2,3,4,5,10,12,13,14,15,19,20,21 -D3)+(D6+k2h(s+an-1λ+β+p))(g(s)- g(s+∂))+(h(s+p)-k1(D5+h(s+∂+p))] 其中记 D1=h(s)-h(s+p) D2=h(s+an-1λ)-h(s+an-1λ+p) D3=g(s+an-1λ)-g(s+an-1λ+β) D4=h(s+an-1λ+β)-h(s+an-1λ+β+p) D5=h(s+an-1λ+p)-h(s+an-1λ+β+p) D6=h(s+∂)-h(s+∂+p) D7=g2(s+an-1λ)-g2(s+an-1λ+p) D8=h(s+∂+p)-h(s+an-1λ+β+p) N=D8+(D6+k2h(s+an-1λ+β+p))g(s+∂)] 3.1系统的可用度 定理1系统的瞬时可用度为A(t),其Laplace变换A*(s)和稳态可用度A分别为 (1) (2) 其中 Λ0=Γ1+Γ2 证明由系统瞬时可用度定义得 3.2系统的故障频度 定理2系统的瞬时故障频度为W(t),其Laplace变换为 (3) 稳态故障频度为 (4) 其中 证明由文献[15],有 3.3系统等待修理的概率与修理工休假的概率 定理3记t时刻,系统等待修理的概率与修理工休假的概率分别为P1(t),P2(t),其Laplace变换分别为 (5) (6) 系统等待修理概率和修理工休假概率的稳态结果分别为 (7) (8) 其中 (1-h(s+∂))+∂k1k4N+(D4+D7M+k1D6+ (1-h(s+an-1λ+β+p) (1-h(an-1λ+β+p) k1k2h(an-1λ+β+p))(1-g(0))+ 证明 作Laplace变换,并将相应各状态方程的解带入即可得式(5)和(6),再根据Tanber定理,并应用洛必达法则,得式(7)和(8)。 由偏微分方程理论可得微分方程组: βQ1(t,x) 初始条件:Q0(0,0)=1,其余为0,边界条件: Qi(t,0)=0,i=1,2,3,4,5,10,12 对上述各式作Laplace变换并求解可得相应的 定理4系统可靠度R(t)的Laplace变换为 (9) 系统首次故障前的平均时间为 (10) 其中 (1-h(an-1λ+β+p)) 证明由可靠度定义得 若系统的部件能够修复如新,且两个部件同型,即系统转化为开关连续型且修理工多重休假的两同型部件温贮备系统,其相关可靠性指标见文献[10]。 若系统的转换开关完全可靠,且转换瞬间完成,即系统转化为转换开关完全可靠的修复非新的温贮备系统。假定两部件的工作时间、修理时间、贮备时间以及修理工休假时间的分布都与上述模型中的假定一样,用补充变量法和广义Markov过程,再用Laplace变换,得到系统的稳态指标。 稳态可用度 (11) 稳态故障频度 (12) 其中 Δ0=1-g2(an-1λ)[h(an-1λ)-h(an-1λ+β)]+e-bn-1μy[h(∂)-h(∂+an-1λ)] g2(an-1λ)[h(an-1λ)-h(an-1λ+β)] h(∂+an-1λ)] 本文研究了由两个不同部件、一个修理工组成的开关不完全可靠的温贮备可修系统,考虑了在开关寿命连续型、修理工多重休假和部件1不能修复如新的条件下,利用补充变量法和Laplace变换等工具得到了系统的主要可靠性指标。本文研究结果是在已有文献研究结果上的进一步延伸,具有一定的理论价值,为工程实践和实际生活提供了有力的依据。 [1] 曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社,2006. [2] 程侃.寿命分布类与可靠性数学理论[M].北京:科学出版社,1999. [3] 刘海涛,孟宪云,李芳,等.两个不同型部件温贮备系统的几何过程模型[J].系统工程,2010,28(9):103-107. [4] 张建龙,孟宪云.有优先权的三状态温贮备可修系统的可靠性分析[J].辽宁工程技术大学学报:自然科学版,2012,31(1):98-101. [5] YUAN L,MENG X Y.Reliability analysis of a warm standby repairable system with priority in use[J].Applied Mathematical Modelling,2011,35(9):4295-4303.[6] WANG K H,SIVAZLIAN B D.Reliability of a system with warm standbys and repairmen[J].MicroelectronReliab,1989,29(5):849-860. [7] 孟娅丽,郑海鹰.修理工可多重休假的温贮备系统[J].浙江大学学报:理学版,2012,39(5):517-523. [8] 张静,岳德权,王丽花.修理工休假的温贮备可修系统的瞬时可用度分析[J].中山大学学报:自然科学版,2011,50(5):28-33. [9] 吴清太.2个不同部件组成的开关寿命连续型温贮备系统的可靠性分析[J].南京理工大学学报,2004,28(6):673-678. [10] 张民悦,邬一凡.具有多重休假开关连续型温贮备可修系统的可靠性分析[J].兰州理工大学报,2015,41(5):152-156. [11] 刘海涛,孟宪云.具有单重休假和修复不如新的两部件温贮备系统[J].自动化学报,2012,38(4):639-646. [12] 吕文静,郑海鹰.修理工可延误休假且部件不能修复如新的温贮备可修系统[J].浙江大学学报:理学版,2014,41(5):512-517. [13] 金宇,孟宪云.具有多重休假和修复非新的Gaver并联系统[J].郑州大学学报:理学报,2015,47(3):7-16. [14] 马淑莲,汪云芬.具有单重休假和修复不如新的两部件并联系统[J].数学的实践与认识,2011,41(16):111-116. [15] 史定华.计算可修系统在(0,t]中平均故障次数的新方法[J].应用数学报,1985,8(1):101-110. Switch-continuous and Non-new Workpiece-composed Repairable Warm Standby System ZHANGMinyue,LIANAiling (School of Science, Lanzhou University of Technology, Lanzhou 730050, China) Taking consideration of the incomplete reliability of switches and the non-new workpiece-composed repairable warm standby system, as well as the multiple vacation of repairman, the lifetime and storage time of workpieces, the durability of switches and the repair time of workpiece one are assumed to follow the exponential distribution; and that the multiple vacation of repairman and the repair time of switches and workpiece two are assumed to follow the ordinary continuous distribution. Supplementary variable method is applied to extend as Markov Modal in broad sense and to establish differential calculus equation. Laplace Transform and Inversion are applied to gain systemic reliability indexs such as system availability, system failure repeatability, probability of waiting to be repaired for system, probability of repairman is on vacation, system reliablity and mean time to first time. Finally, a concrete example is given under the warm standby repairable system under completely reliable switch which has approach of multiple vacation for repairman and repair non-new. the service time of continuous switch; non-new and repairable; multiple vacation of repairmen; supplementary variable approach; Markov Modal in broad sense; Laplace Transform 2016-11-21 甘肃省自然科学基金(3ZS042-B25-016);甘肃省科技计划项目(1508RJZA101) 张民悦(1958-),男,河南南乐人,教授,主要从事可靠性数学理论及其应用方面的研究,(E-mail)zhangminyue@lut.cn; 连爱玲(1990-),女,甘肃白银人,硕士生,主要从事可靠性数学理论及其应用方面的研究,(E-mail)1558201667@qq.com 1673-1549(2017)02-0090-08 10.11863/j.suse.2017.02.18 O213.2 A

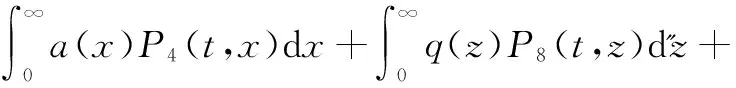



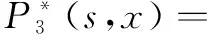
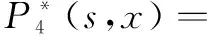



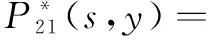



3系统的可靠性分析
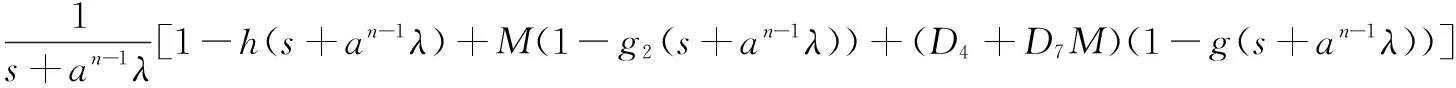












4系统的可靠度和首次故障前的平均时间

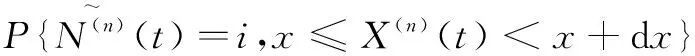
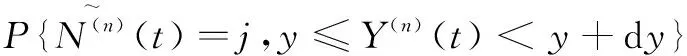



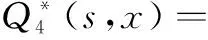

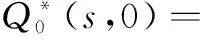

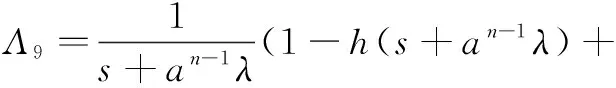

5实例分析
6结束语
