虚拟最劣解与灰色关联度改进的理想解法及其应用

2017-04-27李美娟魏寅坤徐林明

福州大学学报（哲学社会科学版） 2017年2期

关键词：关联度排序灰色

李美娟魏寅坤徐林明

( 1. 福州大学经济与管理学院，福建福州 350116； 2. 中国科学院科技政策与管理科学研究所，北京 100190)

虚拟最劣解与灰色关联度改进的理想解法及其应用

李美娟1, 2魏寅坤1徐林明1

( 1. 福州大学经济与管理学院，福建福州 350116； 2. 中国科学院科技政策与管理科学研究所，北京 100190)

理想解法是有效的多属性决策方法，但是存在逆序性的问题，而且只能反映决策方法的位置，不能反映决策方案数据曲线相似程度。而灰色关联度能很好地反映出数据曲线相似程度。结合虚拟最劣解的思路与灰色关联度的思路，提出一种新的理想解法，既能够克服逆序性，又能反映决策方案之间的相似性。

灰色关联度；虚拟最劣解；理想解法

引言

理想解法，又名双基点法，是由C.L.Hwang和K.Yoon两位学者提出的。[1]理想解法是通过构造多属性决策方案的理想解与负理想解，并以靠近理想解和远离负理想解两个基准，作为评价各方案的判据。先计算每一个决策方案与理想解、负理想解的欧氏距离，再计算各方案与理想解、负理想解的相对贴近度，根据相对贴近度进行排序，相对贴近度越大，方案越优。理想解法，是一种非常有效的多属性决策方案,被广泛地运用到各个领域。李沙浪、雷明运用理想解法评价省级区域低碳经济发展的情况。[2]朱卫东、吴鹏把理想解法引入到风险预警领域。[3]张春海、孙健、刘长花用理想解法对区域科技人才的开发水平进行评价研究。[4]龚豪、杨晨运用理想解法对企业的技术创新联盟组织形式进行研究。[5]

经过学者的深入研究，发现欧氏距离的理想解法存在着排序结果不合理的问题。当一个决策方案同时与最优解、最劣解距离都很近，此时决策方案的排序将会出现不合理的情况。[6]针对上述这种缺陷，学者们提出了相应的改进措施。华小义、谭景信使用正交投影法，让垂面距离替换欧氏距离。[7]陆伟锋、唐厚兴利用绝对正负理想点替换正负理想点，使用投影方法计算贴近度。[8]陈伟通过决策者自行设定或者通过咨询有关专家的意见设定绝对理想解和绝对负理想解，用绝对理想解、绝对负理想解替代理想解、负理想解。[9]刘树林、邱菀华通过用夹角余弦来度量决策方案与理想解、负理想解的距离。[10]胡永宏通过设定一个全新的虚拟最劣解，用虚拟最劣解替代最劣解，很好地解决了排序不合理的问题。[11]

灰色关联度用于计算两数据序列的趋势变化趋同程度。如果两数据序列趋势变化程度越相近，则灰色关联度越大。[12]多属性决策不仅要考虑决策方案的位置之间的差异，也要考虑决策方案变化趋势之间的关系。在多属性决策中，人们对于指标的选择具有一定的主观性，并且人们对于事物的认识都是不断发展、不断完善的。因此，在多属性决策中，随着研究的深入，指标体系的建立也在不断完善。这样的决策所呈现出是信息不充分的灰色系统。灰理论处理这些信息不充分的灰色系统具有得天独厚的优势。李海东、王帅、刘阳结合灰色关联度与理想解法评价了区域协同发展。[13]梅丽结合灰色关联分析和熵值理想解法评估了中国31个地区的贫困程度。[14]本文拟结合虚拟最劣解与灰色关联度提出一种新的理想解法。

一、欧氏距离的理想解法(传统的理想解法)

在一多属性决策问题中，有m个待决策方案，n个属性，指标值zij(1≤i≤m,1≤j≤n)。

(一)决策矩阵正向规范化处理

原始的决策矩阵，经过数据正向化处理xij(m×n)，通过规范化处理后，得到决策矩阵yij(m×n)

(二)选取各属性最大值作为最优解

(三)选取各属性最小值作为最劣解

(四)计算决策方案与最优解的欧氏距离

(五)计算决策方案与最劣解的欧氏距离

(六)计算相对贴近度

根据相对贴近度对决策方案进行排序。相对贴近度数值越大，决策方案越好；相对贴近度数值越小，决策方案越差。

二、灰色关联度的理想解法

灰色关联度用于衡量两数据序列的趋势变化趋同状态，以数据曲线相似程度作为灰色关联度的标准。两数据曲线越相似，则关联度越大。若决策方案的数据曲线与最优方案的数据曲线的关联度大，则表示决策方案与最优解越相似；若决策方案的数据曲线与最劣方案的数据曲线的关联度大，则表示决策方案与最劣解越相似。决策方案的评价标准为：决策方案与最优解相似程度高，与最劣解相似程度低，即为最佳的决策方案。通过计算灰色关联度的相对贴近度，根据灰色关联度的相对贴近度对决策方案进行排序，相对贴近度越大，则表明决策方案越优。

(一)原始决策矩阵属性值正向化处理，规范化后，得到决策矩阵yij(m×n)

(二)选取每个属性下的最大值构建最优解

(三)选取每个属性下的最小值构建最劣解

(四)计算每一个决策方案与最优解的灰色关联度

计算第i个决策方案第j个属性与最优解的灰色关联系数

(5)

分辨系数取ρ=0.5。

(五)计算第i个决策与最优解的灰色关联度

(六)计算每一个决策方案与最劣解的灰色关联度

计算第i个决策方案第j个属性与最劣解的灰色关联系数

分辨系数取ρ=0.5。

(七)计算第i个决策与最劣解的灰色关联度

(八)计算相对贴近度

根据相对贴近度对决策方案进行排序。决策方案的评价标准为：决策方案与最优解越相似，与最劣解越不相似，即为最佳的决策方案。根据灰色关联度的相对贴近度对决策方案进行排序，相对贴近度越大，则表明决策方案越优。相对贴近度数值越大，决策方案越好；相对贴近度数值越小，决策方案越差。

三、基于虚拟最劣解与灰色关联度改进的理想解法

因为欧氏距离存在排序不合理情况，本文采用胡永宏的虚拟最劣解的想法。虚拟最劣解也只解决了欧氏距离排序不合理情况，在数据相似程度上依然存在不能表达的缺陷，利用灰色关联度替代欧氏距离，就能表示数据曲线之间的相似性。结合以上两种思路，提出新的理想解法，定义一种新的贴近度的计算方法。

(一)虚拟最劣解的理想解法

(1) 原始决策矩阵所有属性值正向化后，经过规范化处理，得到决策矩阵

(2) 选取每个属性下的最大值构建最优解

(3) 选取每个属性下的最小值构建最劣解

(4) 构建虚拟最劣解

(5) 计算每一个决策方案与最优解的距离

(6)计算每一个决策方案与虚拟最劣解的距离

(7) 计算相对贴近度

(二)灰色关联度的理想解法

(1) 原始决策矩阵所有属性值正向化后，经过规范化处理，得到决策矩阵

(2) 选取每个属性下的最大值构建最优解

(3) 选取每个属性下的最小值构建最劣解

(4) 计算每一个决策方案与最优解的灰色关联度

计算第i个决策方案第j个属性与最优解的灰色关联系数

分辨系数取ρ=0.5。

(5) 计算第i个决策与最优解的灰色关联度

(6) 计算每一个决策方案与最劣解的灰色关联度

计算第i个决策方案第j个属性与最劣解的灰色关联系数

分辨系数取ρ=0.5。

(7) 计算第i个决策与最劣解的灰色关联度

(8) 计算相对贴近度

(三)定义一个新的贴近度

决策方案优劣的评价标准：根据新的贴近度对决策方案进行排序。若某决策方案的贴近度越大，表示该决策方案越优；若某决策方案的贴近度越小，表示该决策方案越劣。

α与β只要满足α+β=1(0<α<1,0<β<1)，α与β数值根据决策者不同的偏好来设定。若α=0，β=1，就是灰色关联度的理想解法的算法，考虑决策方案数据曲线之间的相似程度。若α=1，β=0，就是通过引进虚拟最劣解的理想解法，不会发生排序不合理的情况，但是只考虑决策方案位置之间的差异，没有考虑数据曲线之间的相似程度。

新理想解法既考虑了决策方案之间位置的差异，也考虑了决策方案的数据曲线的相似程度，是一种有效的多属性决策方案。

四、算例分析

为了证明新的理想解法的有效性，本文使用新的理想解法来评价区域协同创新能力。

(一)区域协同创新能力指标的建立

指标的建立应该满足科学性、现实性、整体性、可操作性、动态连续性这五个原则。中国科技发展战略研究小组《中国区域创新能力报告》建立了知识创造能力、知识流动能力、企业技术创新能力、技术创新环境、技术创新的区域创新能力等5个方面的指标。TomasHellstrm提出从6个维度去评价产学研的创新绩效：产学研网络的发达程度、产学研的研究、经济产出、教育、出版物、专利。[15]曹静、范德成、唐小旭认为产学研结合绩效应基于要素和过程两个维度，对合作创新环境、合作创新投入、合作创新产出、合作创新运行和合作创新效果等5个具体指标进行评价。[16]楼高翔、曾赛星认为协同创新能力要从成员、过程、形式三个不同方面进行评价。[17]廖娟、付丙海、崔有祥基于三重螺旋理论，运用两阶段DEA评价协同创新效率。[18]目前大多数学者是从投入、过程、产出三个角度建立评价指标体系。本文吸取前人在评价指标建立的原则，建立一套基于协同创新投入、协同创新环境支持、协同创新产出的区域协同创新能力评价指标体系。

从三重螺旋理论[19]角度，产学研协同创新参与主体有政府、高校、科研院所、企业，建立的评价指标体系必须涵盖这四大主体。产学研协同创新的主体高校和科研机构作为基础研究的主要阵地，肩负着知识生产的任务。企业作为技术的需求方，更加强调应用研究。协同创新能够使基础研究的科研成果更迅速地得到应用。

协同创新投入从高校、科研机构、企业三个主体角度进行度量，主要包括人力、财力的投入，人力的投入用R&D人员全时当量来衡量，财力投入用R&D经费内部支出来衡量。

外部环境和企业对于高校和科研机构的资金的支持会对产学研协同创新产生积极的影响。政府的支持，选用R&D经费内部支出来自政府来衡量。企业、科研机构、高校则使用各自的R&D外部支出来衡量。(科研机构外部支出在某些地区数据缺失，只能删除科研机构的指标)。

协同创新产出包括科研产出、经济效益。科研产出主要是学术和科技活动的直接产出，包括发表的科技论文、科技著作、有效专利。经济效益包括专利许可数收入、新产品开发项目数、新产品销售收入(在科技统计年鉴中，专利转让收入数据有缺失，只能把这个指标删除)。

综上所述，建立区域协同创新能力评价指标体系如表1所示。

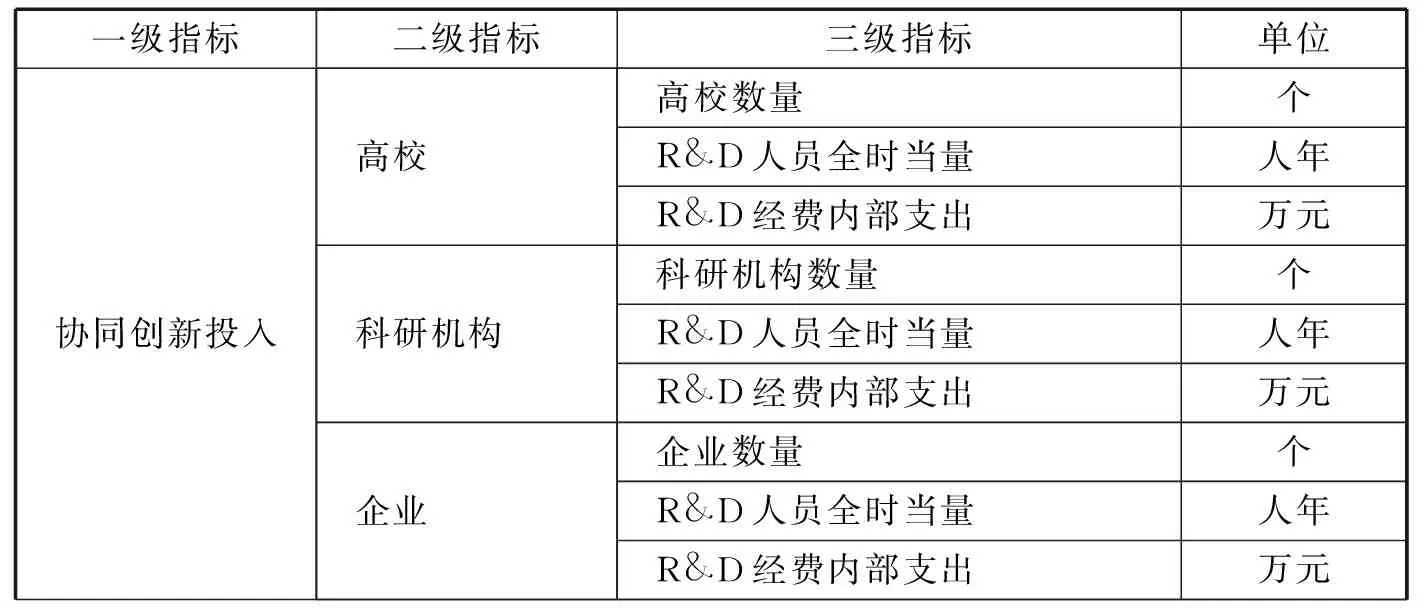
表1 区域协同创新能力评价指标

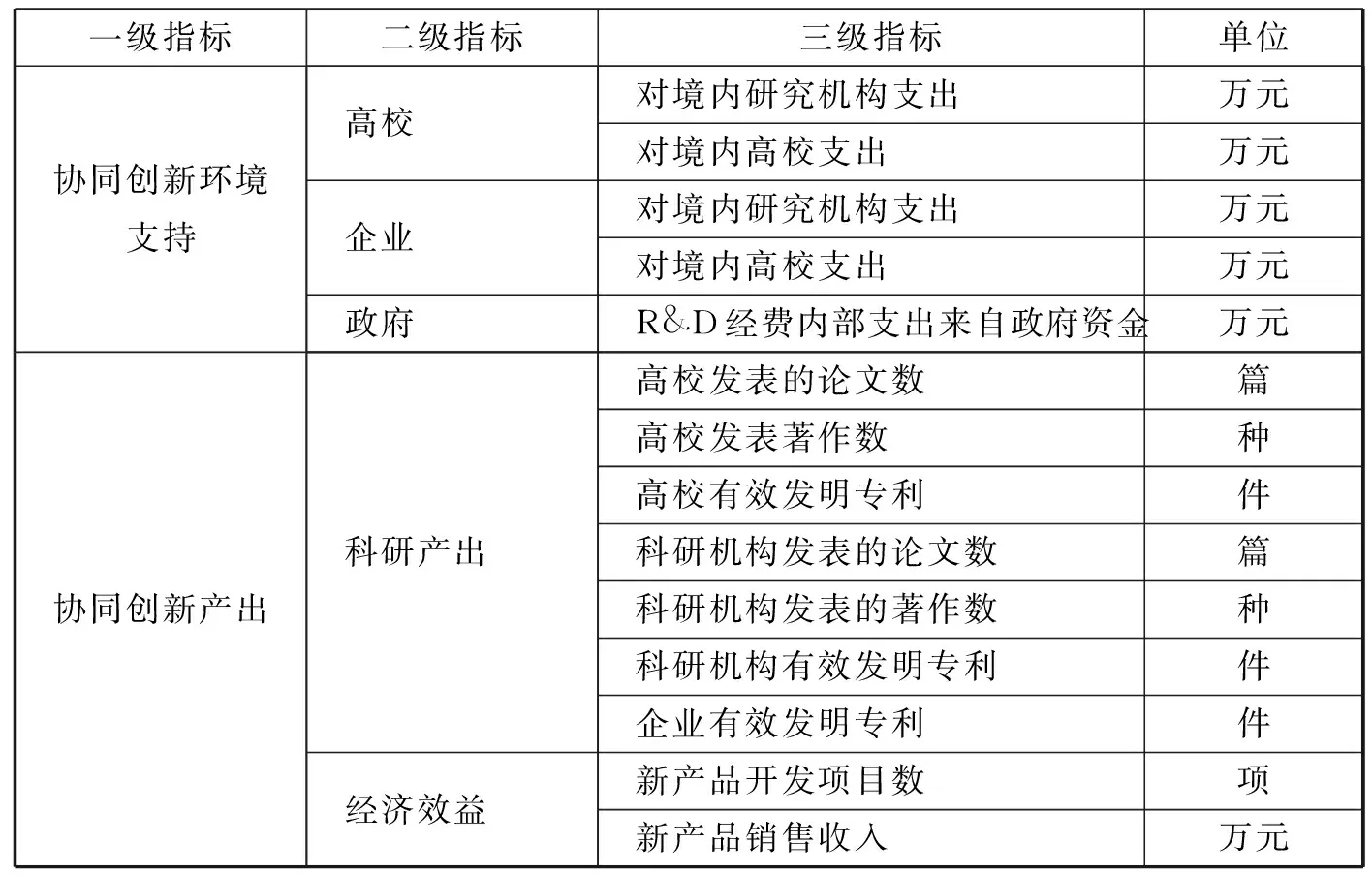
续表1

注：科研机构为统计年鉴中的研究与开发机构，企业为统计年鉴中的规上工业企业，论文数为科技论文，著作为科技著作。

(二)算例分析

本文以α=0.5，β=0.5的权重分别赋予虚拟最劣解的贴近度、灰色关联度的贴近度。以31个省级行政区作为区域划分的标准，所有数据均来自《2014年中国科技统计年鉴》。计算的结果如表2所示。

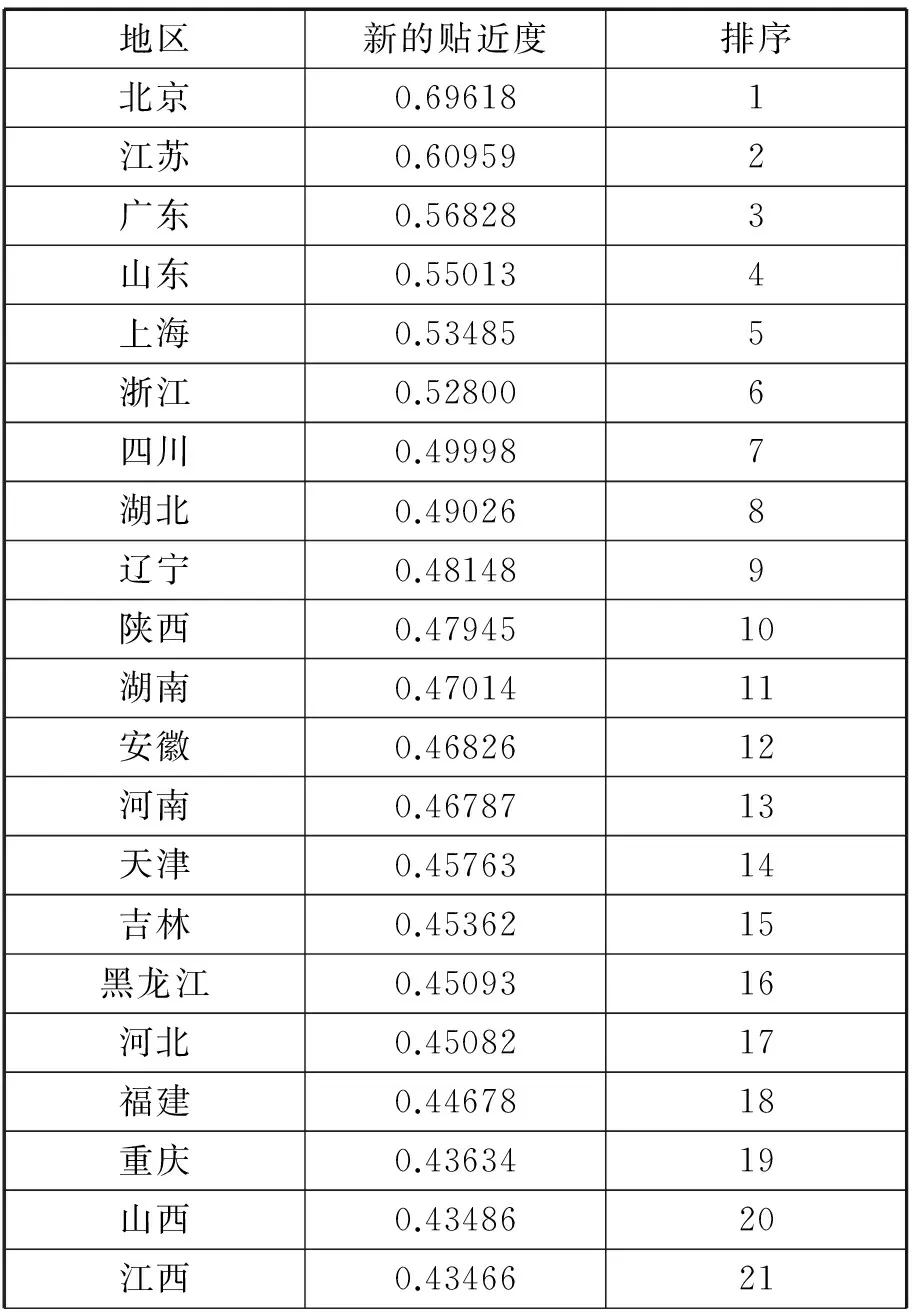
表2 31个省级行政区协同创新能力排序

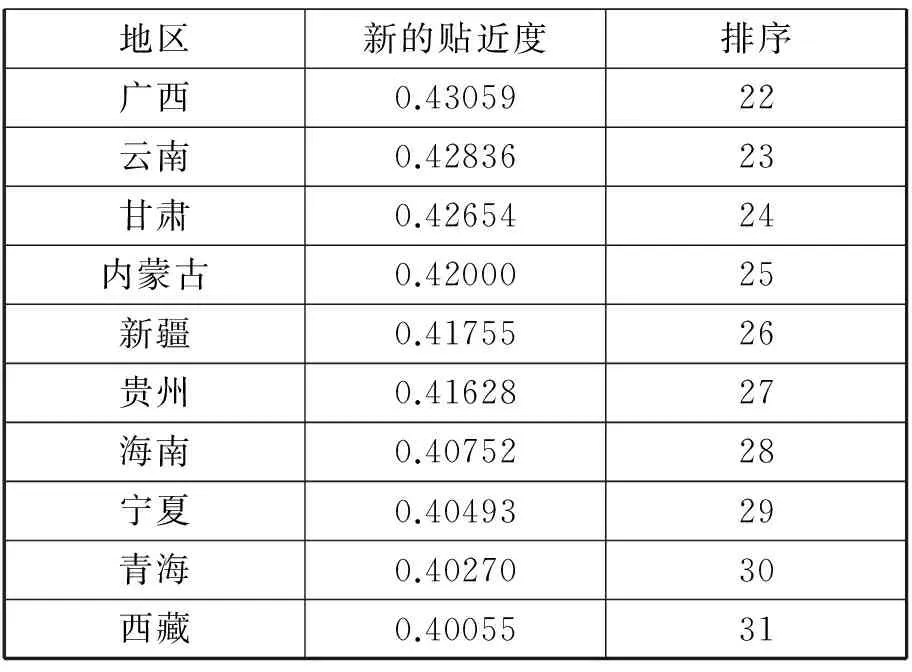
续表2

根据新的贴近度，本文把31个省级行政区划分为四类。

第一类，贴近度大于0.6，一共有2个地区，分别是北京、江苏。

第二类，贴近度大于0.5，且小于或等于0.6，一共4个地区，分别是广东、山东、上海、浙江。

第三类，贴近度大于0.45，且小于或等于0.5，一共11个地区，分别是四川、湖北、辽宁、陕西、湖南、安徽、河南、天津、吉林、黑龙江、河北。

第四类，贴近度大于0.4，且小于或等于0.45，一共14个地区，分别是福建、重庆、山西、江西、广西、云南、甘肃、内蒙古、新疆、贵州、海南、宁夏、青海、西藏。

如果只考虑虚拟最劣解的贴近度，即权重取值α=1，β=0，所得结果是以决策方案的位置差异作为评价标准，却忽略了数据曲线之间的相似性的影响。如果只考虑灰色关联度的贴近度，即权重取值α=0，β=1，所得结果是以决策方案数据曲线的相似性作为评价标准，却忽略了决策方案的位置的影响。

(三)排序结果比较

为了验证本方法的有效性，本文将虚拟最劣解的理想解法、灰色关联度的理想解法、基于虚拟最劣解与灰色关联度改进的理想解法三种方法的排序结果进行对比。排序结果如表3所示。

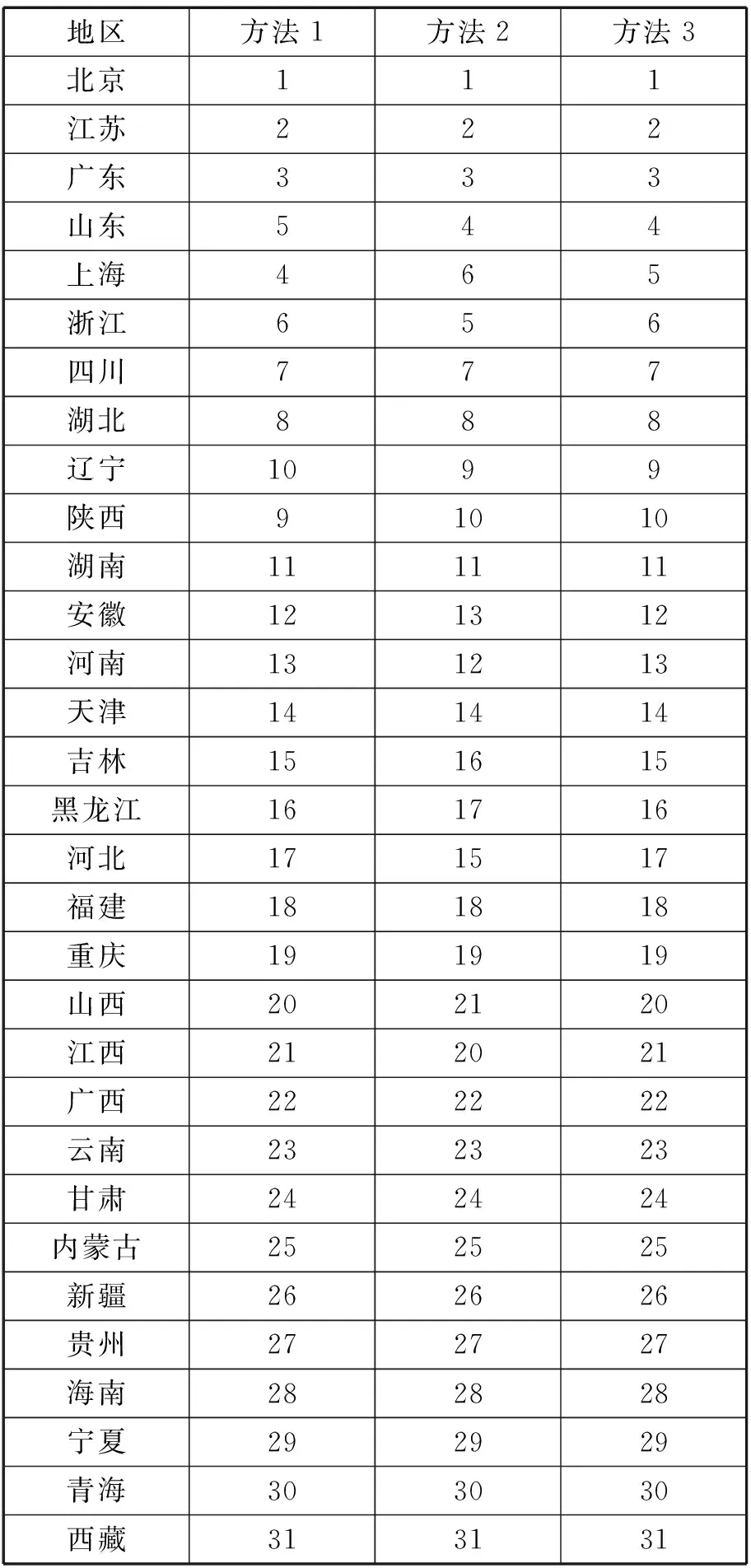
表3 三种方法排序结果

注：方法1为虚拟最劣解的理想解法，方法2为灰色关联度的理想解法，方法3为基于虚拟最劣解与灰色关联度改进的理想解法。

从表3可以看出虚拟最劣解的理想解法、基于虚拟最劣解与灰色关联度改进的理想解法两种方法的比较结果大致相同，两种方法出现的排序结果出现差异的地区是上海、山东、辽宁、陕西4个地区。在虚拟最劣解的理想解法这4个地区排序结果的是：上海第4、山东第5、陕西第9、辽宁第10；基于虚拟最劣解与灰色关联度改进的理想解法这4个地区排序结果是上海第5、山东第4、陕西第10、辽宁第9，这4个地区在两种方法下排序的结果只相差一个位次。出现的差异的原因是基于虚拟最劣解与灰色关联度改进的理想解法还包含了数据序列之间趋同程度的表达。

表3表明灰色关联度的理想解法、基于虚拟最劣解与灰色关联度改进的理想解法两种方法的比较结果大致相同，两种方法出现的排序结果出现差异的地区是：上海、浙江、安徽、河南、吉林、黑龙江、河北、山西、江西。灰色关联度的理想解法的是：浙江第5、上海第6、河南第12、安徽第13、河北第15、吉林第16、黑龙江第17、江西第20、山西第21。基于虚拟最劣解与灰色关联度改进的理想解法：上海第5、浙江第6、安徽第12、河南第13、吉林第15、黑龙江第16、河北第17、江西第21、山西第20。在两种方法下，出现排序结果差异的地区除了河北排序结果相差两个位次，其余地区只相差一个位次。出现差异的原因是基于虚拟最劣解与灰色关联度改进的理想解法还包含了位置之间的差异性。

比较不同权重组合下，排序结果的影响，本文选取了三个权重组合。组合1为α=0.2、β=0.8，组合2为α=0.5、β=0.5，组合3为α=0.8、β=0.2。排序结果如表4所示。

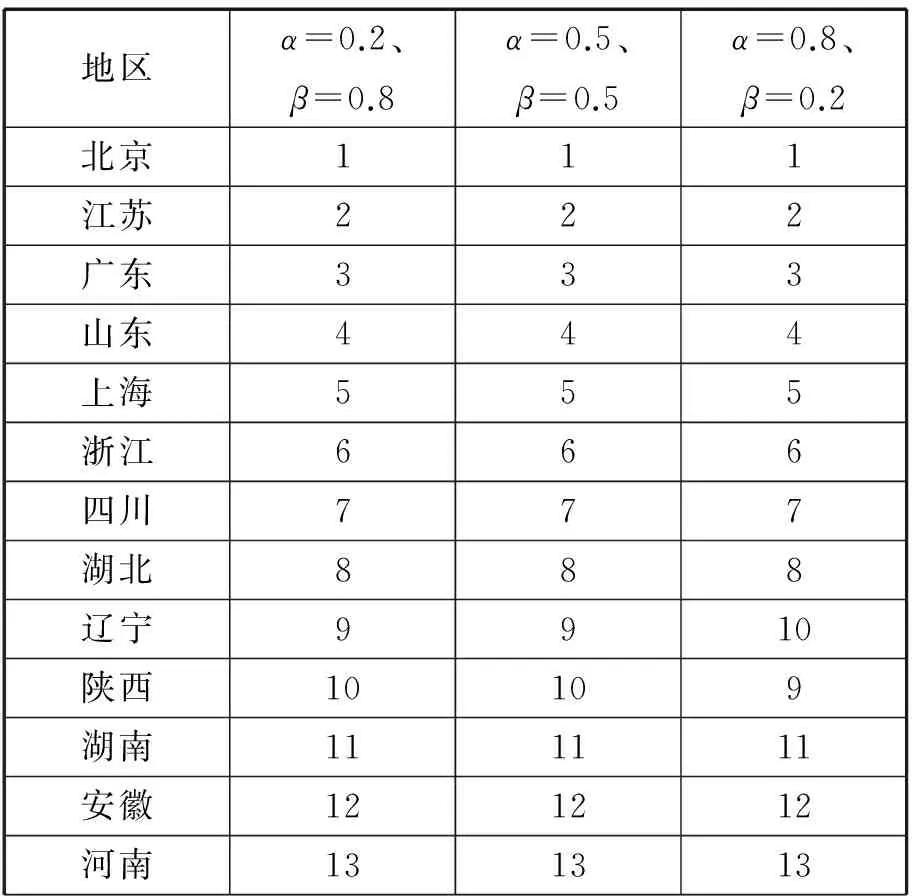
表4 不同组合权重下排序结果

续表4

地区α=0.2、β=0.8α=0.5、β=0.5α=0.8、β=0.2天津141414吉林151515黑龙江171616河北161717福建181818重庆191919山西212020江西202121广西222222云南232323甘肃242424内蒙古252525新疆262626贵州272727海南282828宁夏292929青海303030西藏313131

表4表明，只有辽宁、陕西、黑龙江、河北、山西和江西6个地区在三种不同组合权重下出现差异，差异的原因是不同的组合权重对于虚拟最劣解的理想解法的贴近度、灰色关联度的理想解法的贴近度有不同的偏好，不同的偏好就会对排序结果产生影响。

五、结论

本文结合虚拟最劣解和灰色关联度，提出一种新的理想解法。新的理想解法结合虚拟最劣解与灰色关联度，既能解决经典理想解法的逆序性的弊端，又能反映数据曲线之间的相似性，使得评价结果更加科学合理。α与β的取值取决于决策者的偏好。本文还通过一个具体的算例，证明了新的理想解法的有效性。

注释：

[1]HwangC.,YoonK.,Multiple attribute decision making,BerlinSpringer，1981.

[2] 李沙浪、雷明：《基于TOPSIS的省级区域低碳经济发展评价及其空间面板计量分析》，《中国管理科学》2014年第1期。

[3] 朱卫东、吴鹏：《引入TOPSIS方法的风险预警模型能提高模型的预警准确度吗？——来自我国制造业上市公司的经验证据》，《中国管理科学》2015年第11期。

[4] 张春海、孙健、刘长花：《我国科技人才开发水平的测度研究——基于内地31个省(市、自治区)的TOPSIS模型测算》，《科技进步与对策》2012年第12期。

[5] 龚豪、杨晨：《基于Topsis法的企业技术创新联盟组织形式的选择》，《科技进步与对策》2011年第22期。

[6]ChangC.C.,LinJ.J.,LinJ.H.,“Domesticopen-endequitymutualfundperformanceevalutionusingextendedtopsismothodwithdifferentdistanceapproaches”，Expert Systems with Applications ,vol.37,no.6(2010),pp.4622-4649.

[7] 华小义、谭景信:《基于“垂面”距离的TOPSIS法——正交投影法》，《系统工程理论与实践》2004年第1期。

[8] 陆伟锋、唐厚兴：《关于决策TOPSIS方法的一种综合改进》，《统计与决策》2012年第19期。

[9] 陈伟：《关于TOPSIS法应用中的逆序问题及消除的方法》，《运筹与管理》2005年第3期。

[10] 刘树林、邱菀华：《多属性决策的TOPSIS夹角度量评价法》，《系统工程理论与实践》1996年第7期。

[11] 胡永宏：《对TOPSIS法用于综合评价的改进》，《数学的认识与实践》2002年第4期。

[12] 邓聚龙：《社会经济灰色系统的理论与方法》，《中国社会科学》1984年第4期。

[13] 李海东、王帅、刘阳：《基于灰色关联理论和距离协同模型的区域协同发展研究方法及实证》，《系统工程理论与实践》2014年第7期。

[14] 梅丽：《中国各地区经济福利与贫困测度》，《统计与决策》2015年第16期。

[15]TomasHellstrm，“EvaluatingandManagingthePerformanceofUniversity-IndustryPartnerships”，Evaluation，vol.5,no.3(1999),pp.330-335.

[16] 曹静、范德成、唐小旭：《产学研结合技术创新绩效评价研究》，《科技进步与对策》2010年第7期。

[17] 楼高翔、曾赛星：《区域技术创新协同能力的测度及其评价体系构建》，《企业经济》2006年第11期。

[18] 廖娟、付丙海、崔有祥：《基于三螺旋理论的区域协同创新效率评价研究》，《科技与经济》2015年第3期。