基于PZFlex的超声滚压振子仿真分析

李 龙，高延峰，张 震

（南昌航空大学 航空制造工程学院，南昌 330063）

基于PZFlex的超声滚压振子仿真分析

李 龙，高延峰，张 震

（南昌航空大学 航空制造工程学院，南昌 330063）

研究一种用于超声滚压的夹心式压电超声振子，应用一维纵振波动方程，对其进行结构参数计算。基于理论计算结果，使用有限元软件PZFlex基于时域/瞬态分析方法对其进行谐响应分析及谐振频率下的端面位移振动情况分析，且根据仿真结果，设计并制造了相应的压电超声振子，并采用频率特性分析仪测量得到其实际谐振频率，采用多普勒测振仪测量得到其端面位移振动情况，结果仿真结果与实际测量值符合较好。

夹心式压电超声振子；谐响应分析；时域/瞬态；PZFlex

0 引言

超声滚压利用超声冲击能量和静载荷滚压相结合，对金属零部件表面进行高速撞击处理，使零件表层材料产生较大的塑形变形，卸载后形成有益的残余应力，从而强化被加工表面。与传统的滚压工艺相比，材料塑形变形明显，被加工件表面粗糙度降低，显微硬度、残余压应力得到提高，金相组织也得到细化，从而进一步提高工件耐磨性、耐腐蚀、耐疲劳强度等性能。且超声滚压设备可以直接被安装在车床、铣床、加工中心等加工设备上。

超声滚压振子一般由夹心式换能器和变幅杆构成。其中换能器作为超声滚压最重要的部件之一，其主要组成为前后金属端盖和极化方向与厚度方向一致的压电陶瓷片，由预应力螺栓将三者紧。此结构特点不仅利用了压电陶瓷的纵向振动特性而且能有效避免在大功率工作状态下因陶瓷片抗张强度低造成的压电陶瓷片断裂破损[1]。变幅杆是具有特定函数母线的回转体结构。

PZFlex是针对压电、超声和生物体中的波传播问题而开发的有限元仿真软件包。它采用有限元和直接时域/瞬态方法来解决大型且复杂的1D，2D和3D波动问题。运用显式积分方法求解波的传播、隐式积分方法求解压电材料的混合积分算法，这就极大的降低了求解模型规模，并大大提高了计算速度。对于压电换能器研究中所需的频域计算结果，PZFlex通过离散傅里叶变换获得的，因此，这种方法特别适合于中-高频领域的应用且内置的快而效率高的运算法则生成有一定尺寸和范围的精确的模型，是其他有限元产品所不能企及的。

1 振子的结构设计

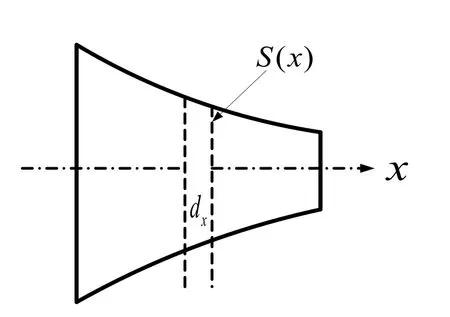
图1 变截面杆的纵振

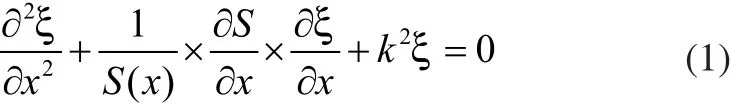
式中：ξ为质点位移函数，ξ=ξ(x)；S为杆横截面积函数；k为圆波数，kk==ω/C；ω为圆频率；C为纵波在细棒中声速，

1.1 换能器结构设计

夹心式压电换能器主要由金属前盖板、压电陶瓷晶堆以及金属后盖板三个基本构件组成如图2所示。从超声换能器功率重量比考虑，总是希望能以较小的重量产生较大的输出振动能量；超声振子设计中换能器通常为半波长或四分之一波长[3]，由纵振波动原理可知：若换能器为半波长，变幅杆长度为半波长的整数倍，振子总长至少为一个波长；换能器前端盖与变幅杆一般由螺栓连接，其结合面总有能量损耗容易形成阻挡层，此结合面为节面有利于声波传输，若为半波长变幅杆次结合面为节面输出端位移为零。基于以上原因将夹心式换能器设计为四分之一波长即l3等于零，且将换能器与变幅杆结合面定位“节面”即此处的边界条件为位移为零。其中堆叠压电片可等效声速C2为：

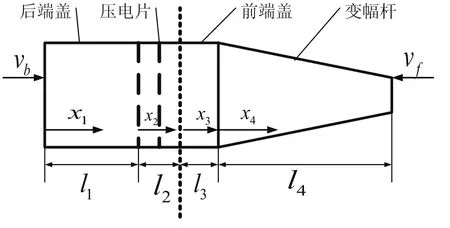
图2 振子结构

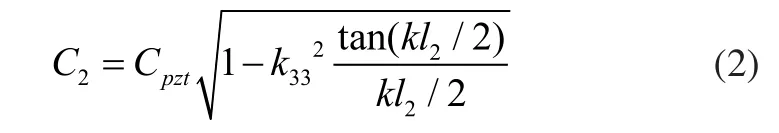
式中：Cpzt为压电陶瓷声速；k33为机电耦合系数。

各边界条件为式(3)，得换能器频率方程为式(4)：

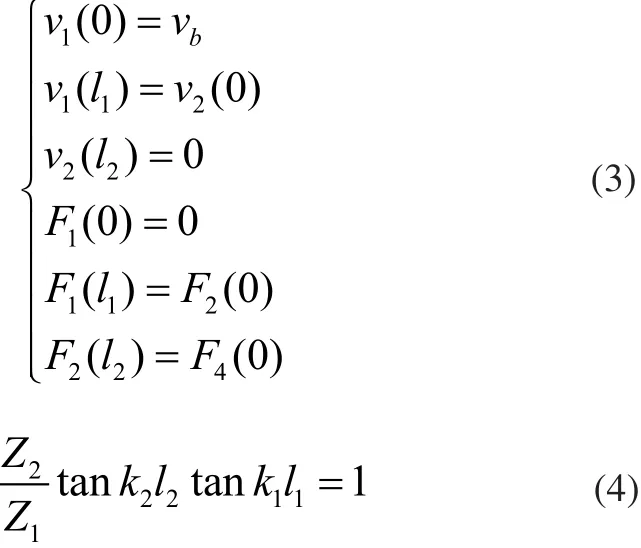
式中：vb为振子后表面振速；vi(x)、Fi(x)分别为第i段点x的速度、应力；Z为特性阻抗，ZZ==ρcS。

1.2 变幅杆设计

变幅杆的边界条件为式(5)，其频率方程为式(6)：

式中：vf为振子前表面振速；R4、R5分别为变幅杆大端、小端半径。

1.3 参数的计算

设计中工作频率为20kHz。常用压电陶瓷材料有PZT-4、PZT-5、PZT-8等，在超声振动滚压中使用大功率换能器，所以选用抗张强度和稳定性的PZT-8；后盖板材料要求疲劳强度高，选用45#钢；变幅杆选择一般依据工作频率范围内材料损耗小、抗疲劳强度高、声阻抗率小且易于加工等原则，在此选用LY12铝合金。各材料参数如表1所示，后盖板、压电陶瓷片、变幅杆外形尺寸如表2所示。

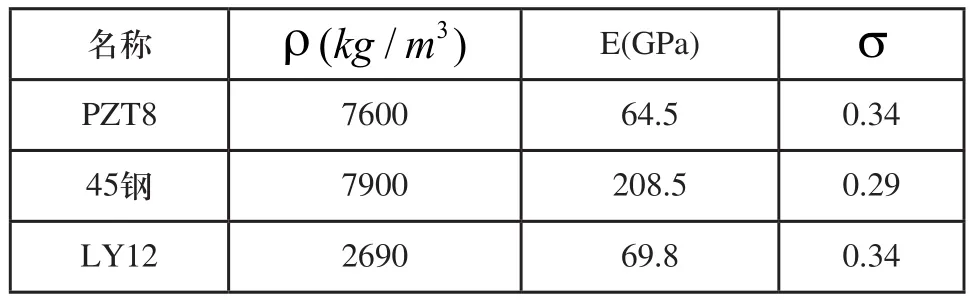
表1 材料参数

表2 振子各组成部件结构尺寸

由式(4)、式(6)及表1、表2各参数可推出l2=10mm，l3=28.99mm，l4=109.15mm。

2 仿真分析

2.1 PZFlex介绍及建模

PZFlex采用混合求解方案，显式积分方法求解波的传播；隐式积分方法求解压电材料。采用有限元（FEM）对振子结构离散化，从而将振子无限自由度求解问题转换为有限个节点自由度求解问题[4,5]，对于后盖板、变幅杆及螺栓等材料基于瞬态动力分析方程式(7)求解其瞬态响应；而对于PZT单元，考虑其压电效应，除动力方程外还要为其节点定义电势自由度，并引入压电方程式(8)描述其力电耦合特性[6]。

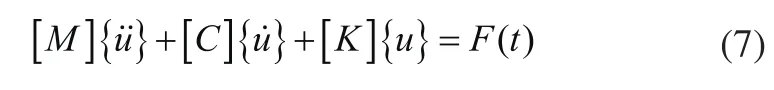
式中：[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；为位移响应，其中为位移幅值向量；F(t)为激励函数。

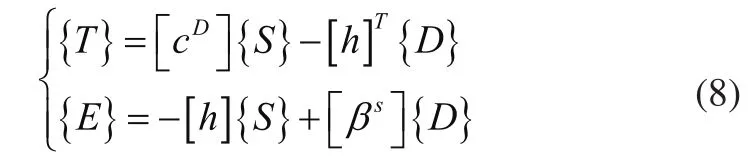
式中：{T}、{S}、{E}、{D}分别为应力、应变、电场强度、电位移矩阵；[CD]、[βS]、[h]分别为弹性系数矩阵、介电系数矩阵和压电系数矩阵。

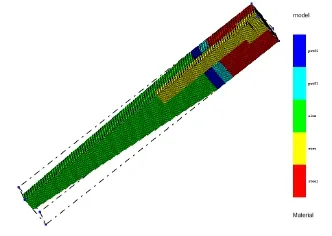
图3 振子网格结构

网格划分：PZFlex使用简单的线性单元网格划分兼顾效率与精确性在此设置为每波长15个网格单元。网格划分后模型如图3所示。

定义材料属性：仿真采用材料属性如上所示，其中为保证两个PZT压电片接触面极性一致，将压电片按极化方向相反设置且接触面为正极。

边界条件：虽然实际工作状态下换能器振子受到工件的负载，但影响较小，且为了简化模拟过程，将其作为整体的边界条件设为自由。

载荷施加：PZFlex作为时域求解器选择加载函数须确保其频率能完全覆盖需要获得频率范围，因此选择频率足够高的正弦驱动函数。模型两片压电片中间正极加载幅值为1、初相位为0、频率为106Hz的正弦电压，两压电片负极置零。

2.2 仿真结果

图4 节点时域位移

选取接近变幅杆输出端面的一个观察节点作为位移输出节点，利用有限元软件PZFlex可得出如图4的观察节点振动位移图，由图可以看出t=0时刻节点位移为零。随着激振的进行，Z方向的位移呈现周期性变大的趋势，当t=0.025s时位移达到最大值，振子振动达到平衡状态。

由瞬态的时域位移图经快速傅里叶变（FFT）可以得到如图5所示幅频特性曲线。可得其第一阶如图5所示为19721Hz。其与设计频率20000Hz误差为1.395%，在误差允许范围内。造成误差原因主要在于：为了简化模型理论设计计算而基于一维纵振波动方程，而实际情况中振子径向尺寸依然对振动纵振情况有影响；连接件螺栓预应力小对振子应力分布的影响，但影响较小。

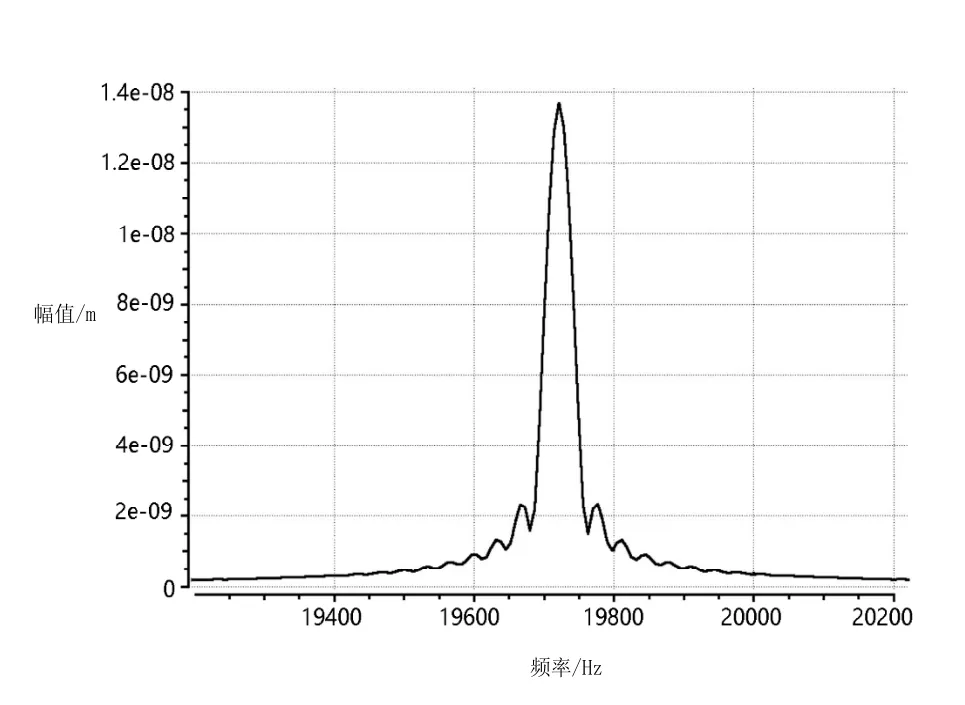
图5 幅频曲线

由PZFlex后处理模块可生成相应的在第一阶共振频率下的压电超声振子的位移云图，如图6所示。由图示可看出振子的使用中节面的确定至关重要，它起着装夹固定整个振动系统的作用，必须在相应频率下节面位移为零，节面的不恰当选择直接影响振子的振动效果，而基于理论计算的节面由于径向尺寸的存在往往与实际情况不符，由图示可知相比于原理论计算的节面，仿真中位移为零的节面发生了轻微的后移。

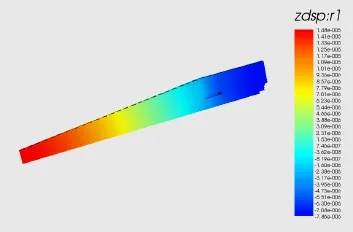
图6 位移云图

3 实物验证

为了对比仿真结果的分析，按文中所提材料PZT-8、45#钢、LY12铝合金及理论计算尺寸设计并制作一个换能器振子，如图7所示。由频率特性分析仪（日本NF公司FRA5022）对其进行频率特性分析，利用多普勒测振仪对其在第一阶共振频率下的振动位移情况进行测试。

图7 振子实物

FR5022A频率特性分析仪覆盖超低频0.1mHz到高频15MHz。可进行一次扫描最多达2万点的高密度测量。频率分辨率0.1mHz。振幅精度±0.05dB、相位精度±0.3°；动态范围140dB。由频率特性分析仪（日本NF公司FRA5022）对其进行频率特性分析，结果如图8所示。其共振频率为19.898Hz，与理论计算及仿真结果符合较好。

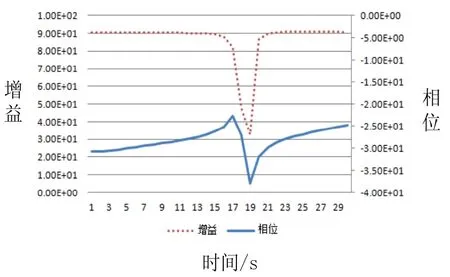
图8 振子频率特性

利用多普勒测振仪对其在第一阶共振频率下的振动情况进行测试，通过信号发生器输出幅值为140V的正弦电压施加于振子，其中多普勒测振仪设置为1μ m/V，由示波器监测得测振仪输出波形图如图9所示，结果显示其峰峰值为7.2V即50nm/V，较理想地符合了预期结果。

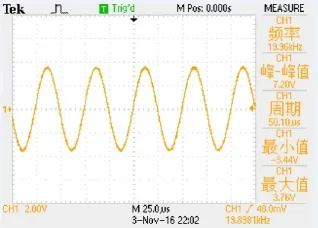
图9 测振仪输出位移

4 结论

从基于一维纵振波动理论计算、PZFlex瞬态仿真对比发现，基于理论计算的结果在一定误差范围内满足基本要求，但从仿真位移云图可看出，在理论节面处，随超声振子径向尺寸的增大，其外表面节面相对理论计算位置偏移也增大，目前主要基于经验调整，还没有较好的理论模型能解决此问题，而PZFlex仿真分析可作为很好的设计依据。实物测试进一步验证了振子具有良好的振动情况，符合预期设计效果。

[1] 林书玉.超声技术的基石——超声换能器的原理及设计[J].物理,2009,03:141-148.

[2] 颜忠余,林仲茂.夹心压电换能器的优化设计——分析各参数对换能器性能的影响[J].声学学报,1995,01:18-25.

[3] 张云电.夹心式压电换能器及其应用[M].北京:科学出版社,2006:70-72.

[4] Shuyu Lin,Shuaijun Wang. Radially composite piezoelectric ceramic tubular transducer in radial vibration[J].IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control,2011,5811.

[5] Iula Antonio,Vazquez Fernando,Pappalardo Massimo,Gallego Juan A.Finite element three-dimensional analysis of the vibrational behaviour of the Langevin-type transducer[J]. Ultrasonics,2002,40:1-8.

[6] 李东明,崔爽,丛琳皓,王道顺,崔玉国.超声轴承用压电换能器结构设计与有限元分析[J].压电与声光,2014,01:53-57.

Simulation research on ultrasonic rolling vibrator based on PZFlex

LI Long, GAO Yan-feng, ZHANG Zhen

TH164

A

1009-0134(2017)04-0096-04

2017-01-11

江西省教育厅科技项目（DA201603059）

李龙（1990 -），男，湖南人，硕士研究生，本科，主要研究方向为精密加工。