仿鲹科机器鱼双体耦合波动推进动力学特性研究

薛文奎，谢 鸥

（1.常州机电职业技术学院 电气工程学院，常州 213164；2.苏州科技大学 机械工程学院，苏州 215009）

仿鲹科机器鱼双体耦合波动推进动力学特性研究

薛文奎1，谢 鸥2

（1.常州机电职业技术学院 电气工程学院，常州 213164；2.苏州科技大学 机械工程学院，苏州 215009）

采用数值模拟方法仿真分析了仿鲹科机器鱼在不同波动频率、波动幅度和初始相位差下的双体耦合波动推进动力学特性，重点研究了同相和反向波动时的阻力和升力系数。实验测试表明：双体机器鱼反相波动耦合推进速度比同相波动高，且游动更稳定。研究结果对仿生水下机器人的研制具有指导意义。

仿鲹科机器鱼；波动推进；耦合；动力学特性

0 引言

鱼类历经数亿年的自然进化，形成了独具特色的游动能力，以适应复杂的海洋环境。受鱼类优越的水下推进机制启发，工程技术人员研发了各种仿生水下航行器[1,2]。此外，生物学家观测发现，80%的鱼类具有群游特性，尤其是小型鱼类，几乎是100%具有群游特性。众所周知，在自然界，单条鱼的力量很弱小，游动动作也很简单，但作为一个群体，鱼类在猎取食饵、逃避敌害和集群洄游等方面表现出惊人的力量。研究表明，鱼类的集群游动蕴含着丰富的流体动力学原理。基于计算流体动力学方法（CFD），研究人员对串行排列的两条仿生机器鱼的游动情况进行了一系列数值模拟分析，结果发现，下游的鱼能从上游鱼产生的尾涡中吸收能量来提高推进效率[3～5]。然而，对于鱼类并行游动的研究却很少见报道，本文将以仿鲹科机器鱼为研究对象，采用数值模拟和实验研究的方法揭示并行排列的仿鲹科机器鱼双体耦合波动推进的动力学特性。

1 问题描述

按照产生周期性游动的生物推进器类型、部位和原理不同，鱼类游动推进模式可分为两大类：身体-尾鳍模式（Body and Caudal Fin, BCF）和中央鳍/对鳍模式（Median and/or Paired Fin, MPF）[6]。鲹科鱼类是典型的BCF游动模式，其通过身体的后半部分在横向方向往复地作扭曲摆动，以横波的方式由前向后传播以获得推进力。如图1所示，并行游动的两条鲹科鱼类，其尾鳍在波动过程中将通过流体互相耦合从而影响其推进性能。根据波动姿态的不同，本文重点研究同相和反相波动时的流体动力学特性。

图1 鲹科鱼类并行游动耦合推进示意图

2 动力学数值模拟分析

2.1 仿真建模

如图2所示，在Fluent软件中建立仿鲹科机器鱼双体耦合波动推进的仿真模型，每个机器鱼由头部和尾鳍两部分组成，采用三角形非结构自适应网格对计算区域进行划分，计算域的左边界为速度入口，初始速度设为v=0.5m/s。采用动网格技术对机器鱼的运动过程进行网格更新，仿鲹科机器鱼的尾鳍运动可采用Lighthill提出的鱼体波动方程进行描述[7]：

式中：yt(xi,t)表示第i条机器鱼的横向位移；c1，c2为波幅包络线系数；xi为第i条机器鱼的x轴坐标值；k为机器鱼的体波波数；ω为机器鱼的体波频率；ϕi为第i条机器鱼的初始相位差；L为机器鱼的尾鳍长度。

本文设两条机器鱼的波动方程参数c1，c2，k和ω为相同的值，按下式控制尾鳍的初始相位差，实现同相和反向波动。

定义仿生推进器沿x轴负方向游动，游动过程的阻力系数Cd和升力系数Cl计算如下：

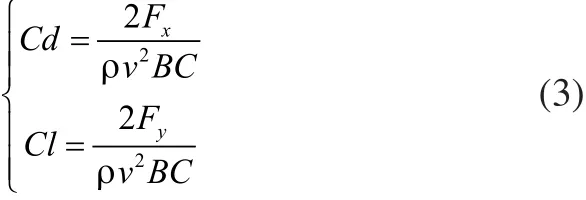
式中：Fx为x轴方向的流体阻力（也即推进力）；Fy为y轴方向的侧向力；ρ为流体密度；B为尾鳍末端的摆幅；B为尾鳍特征弦长；v为来流速度。

Cd表明了机器鱼产生的推进力大小，Cl决定了机器鱼产生的无用功大小。本文采用Cd和Cl两个参数分析仿鲹科机器鱼双体耦合波动推进的动力学特性。

2.2 仿真结果分析

图2 鯵科机器鱼双体耦合推进仿真模型

如图3所示为仿鲹科机器鱼双体耦合波动推进在一个运动周期内的压力云图。由图3(a)可知，反相波动时，在两个机器鱼尾鳍张开阶段T/4，会在尾鳍中部产生一个低压区，同时在各尾鳍的根部会形成一个高压中心，随着尾鳍张开角度变大，高压中心向尾鳍末端移动最后从尾鳍脱落。在尾鳍收合阶段会在尾鳍中部形成高压中心，随着尾鳍的波动，高压中心最后也从尾鳍末端脱落。由图3(b)可知，同相波动时，在两个机器鱼尾鳍上摆过程T/4，上方机器鱼尾鳍的上方会形成一个高压中心，而在下方会形成一个低压中心，随着波动运动的进行，高压和低压中心同时向尾鳍末端移动，最后从尾鳍脱落。尾鳍下摆过程与上摆过程一致，只是高压和低压中心会在下方机器鱼尾鳍上形成。

图3 压力云图

如图4所示为阻力系数和升力系数的时变曲线，由图4(a)可知，同相波动的阻力系数曲线呈类正弦变化，且曲线的频率是波动频率的两倍。反相波动的阻力曲线在一个波动周期内会出现一个尖峰脉冲，对应于两个机器鱼尾鳍收合到一起的时刻。由图4(b)可知，同相波动的升力曲线也呈类正弦变化，曲线的频率与波动频率一致。反相波动的升力曲线则以0为中心呈无规则的波动，且在两个机器鱼尾鳍收合到一起的时刻出现大幅度的抖动。综合对比可知，同相波动能产生平稳的持续推进力，而反相波动能提供瞬时的大推进力。在波动周期的大部分时间里，反相波动产生的升力要小于同相波动，其主要原因是反相波动时两个机器鱼各自尾鳍产生的升力大小基本一致而方向相反，故互相抵消。

图4 两种波动模式下的时变阻力和升力系数曲线（主要参数：摆角30°，频率1Hz，尾鳍间距200mm）

如图5所示为尾鳍摆幅对阻力和升力系数的影响关系曲线。由图5(a)可知，同相波动时，平均阻力系数的绝对值随摆角增大呈线性缓慢增大趋势。反相波动时，平均阻力系数曲线存在一个转折摆角为20°。当摆角小于20°时，平均阻力系数的绝对值随摆角增大而缓慢增大；当摆角大于20°时，平均阻力系数的绝对值随摆角快速增大，其主要原因是：当摆角增大到一定值时，两个机器鱼尾鳍的耦合效应快速增大，从而产生了大的推进力。由图5(b)可知，同相和反相波动的平均升力系数曲线都以0为中心呈无规则的波动，且同相波动的平均升力系数曲线的波动幅值明显比反相波动大，表明同相波动将消耗更多的无用功，效率低。

如图6所示为尾鳍波动频率对平均阻力和升力系数的影响关系曲线。由图6(a)可知，同相和反相波动的平均阻力系数的绝对值都随频率增大而增大，且反相波动的增长速度大于同相波动。由图6(b)可知，同相波动和反相波动的平均升力系数的绝对值随频率的变化也呈无规则的波动。

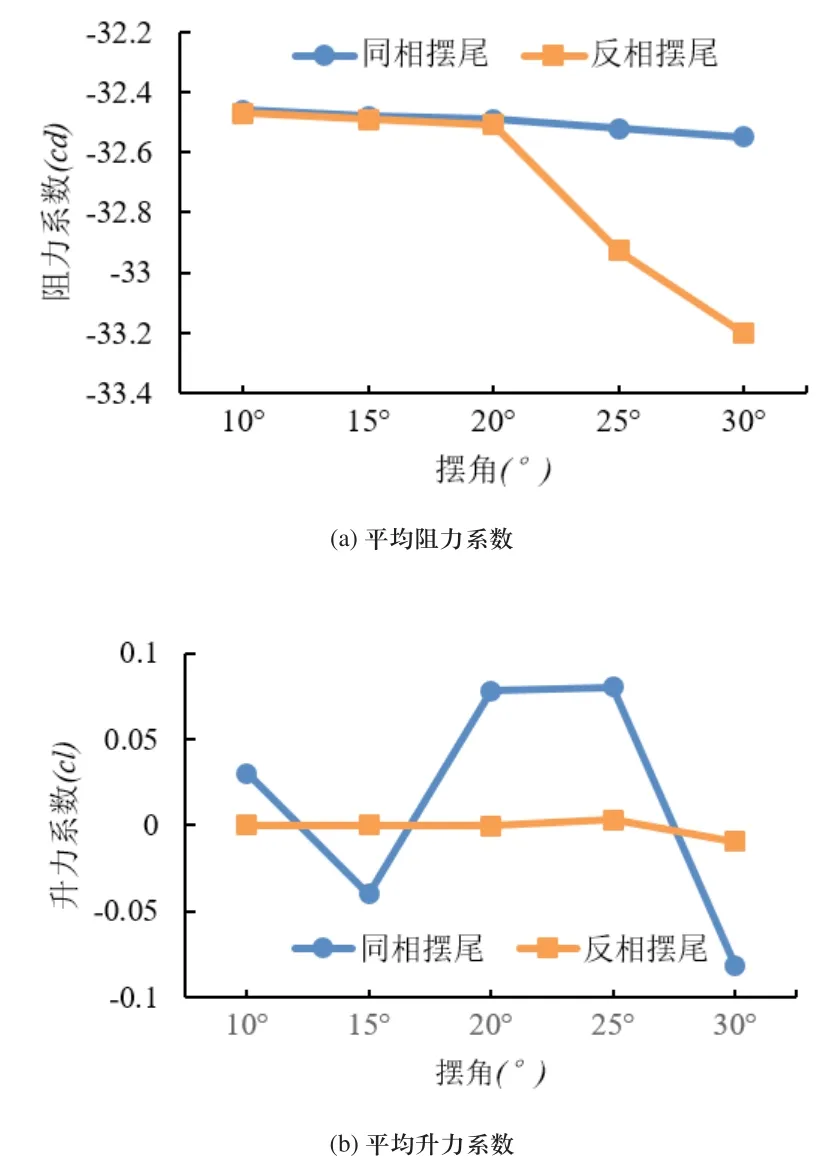
图5 平均阻力和升力系数随摆角幅度的变化关系曲线（主要参数：摆频1Hz，尾鳍间距200mm）

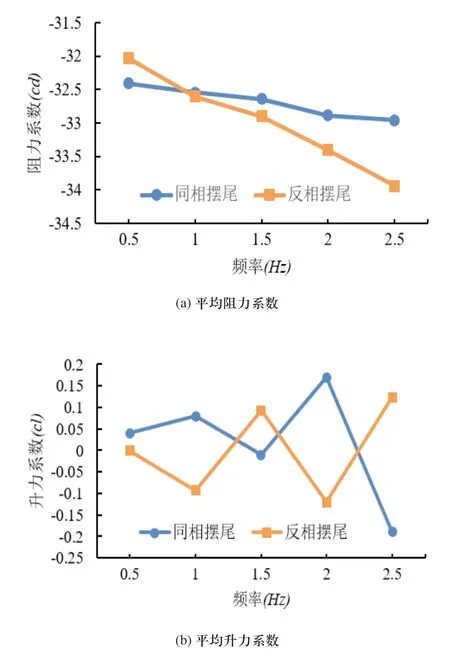
图6 平均阻力和升力系数随波动频率的变化关系曲线（主要参数：摆幅30°，尾鳍间距200mm）

如图7所示为两个机器鱼尾鳍的摆动相位差对平均阻力和升力系数的影响关系曲线。由图7(a)可知，相位差以30°的增量从0°向180°变化时，平均阻力系数的绝对值呈递增趋势，且增长速率开始时较小，当相位差大于120°时增长速度变大。由图7(b)可知，平均升力系数的绝对值在相位差为60°到90°之间时较小，而在其他情况下较大。

图7 平均阻力和升力系数随摆动相位差的变化关系曲线（主要参数：摆幅30°，摆频1Hz，尾鳍间距200mm）

如图8所示为两个机器鱼在不同间距下的同相和反相波动阻力系数曲线。由图8(a)可知，反相波动时，减小尾鳍间距，阻力系数曲线将产生一个大的尖峰脉冲，尤其是间距为150mm时效果很明显，表明两个尾鳍之间产生了强烈的流场耦合效应。相比于反相波动，由图8(b)可知，同相波动时，尾鳍间距对阻力系数的影响甚小。

图8 尾鳍间距对反相和同相波动阻力系数的影响（主要参数：摆角20°，摆频1Hz）

图9 仿鲹科机器鱼双体耦合推进视频截图

3 实验研究

3.1 实验过程

为了验证仿鲹科机器鱼双体耦合波动推进的效果，本文采用自主设计的两条独立的三关节仿鲹科机器鱼通过连杆支架组装为双体耦合推进装置。如图9所示，控制机器鱼尾鳍的初始相位差可实现同相和反相波动推进。采用高速摄影机对机器鱼游动过程进行录像，记录机器鱼游动的距离和时间。将机器鱼游动距离除以游动时间便可获得游动速度，每组实验重复三次取平均值。

3.2 实验结果分析

如图10所示为波动参数对仿鲹科机器鱼双体耦合波动推进速度的影响关系曲线。由图10(a)可知，两种波动方式下，推进速度都随波动频率增大而增大。相同波动频率下，反相波动的速度明显大于同相波动的速度。由图10(b)可知，同相波动时，推进速度随摆幅增大而缓慢增大。反相波动时，推进速度先随摆幅增大而增大，当摆幅大于11cm时，推进速度呈下降趋势。由图9(c)可知，相位差从0°变化到180°时，推进速度呈上升趋势。

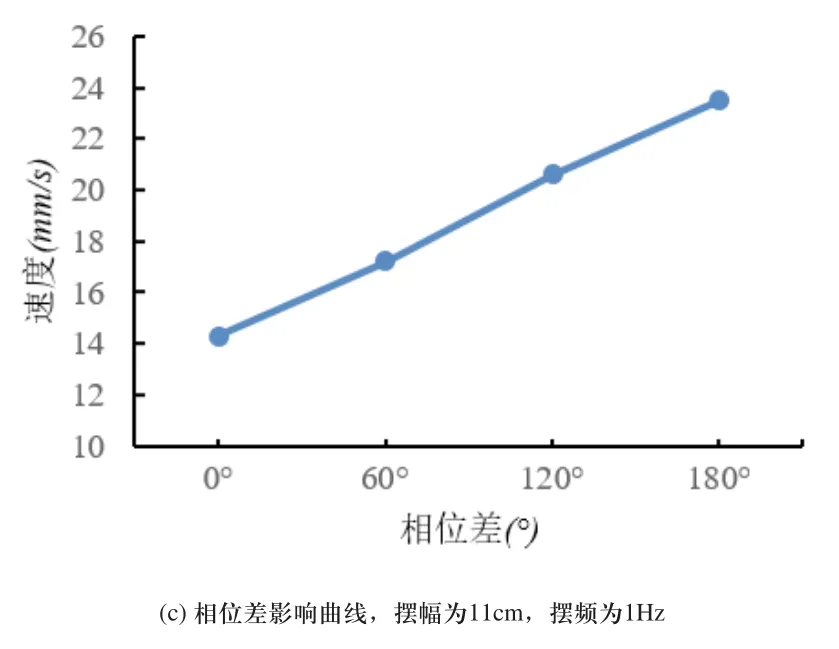
图10 波动参数对仿鲹科机器鱼双体耦合推进速度的影响关系曲线

4 结论

针对鲹科鱼类群游现象，采用CFD方法数值模拟了不同运动参数下仿鲹科机器鱼双体耦合波动推进的动力学特性，并利用自主研发的实验装置对仿鲹科机器鱼双体耦合波动推进的速度进行了测试。结果表明，并行游动的仿鲹科机器鱼，尾鳍之间存在显著流体耦合效应，改变尾鳍的运动参数可对耦合推进力和推进速度进行调节。

[1] 王安忆,刘贵杰,王新宝,等.身体/尾鳍推进模式仿生机器鱼研究的进展与分析[J].机械工程学报,2016,52(17):137-146.

[2] 王扬威,于凯,闫勇程.BCF推进模式仿生机器鱼的研究现状与发展趋势[J].微特电机,2016,44(1):75-80.

[3] Gopalkrishnan R, Triantafyllou M, TriaI1tafyllou G, et a1. Active vorticity control in a shear flow using a flapping foil[J].J Fluid Mech,1994,274(1):1-21.

[4] Deng J, Shao X M, Yu Z S. Hydrodynamic studies on two traveling wavy foils in tandem arrangement[J].Phys Fluids,2007, 19:104-113.

[5] 王亮,毛科峰,陈希,等.鱼游尾迹中射流分布特征的数值模拟研究[J].中国科学,2013,43(9):1097-1104.

[6] C. M. Breder.The Locomotion of Fishes[J]. Zoologica,1926, 4: 159-297.

[7] M. J. Lighthill, Note on the swimming of slender fi sh[J].Journal of Fluids Mechanics,1960,9: 305-317.

Study on dynamic characteristics of two carangiform robotic fish coupling undulation propulsion

XUE Wen-kui1, XIE Ou2

TP242

A

1009-0134(2017)04-0143-05

2017-02-15

国家自然科学基金（51305287）；江苏省自然科学基金（BK20130264）；江苏高校品牌专业建设工程资助项目（TAPP）（PPZY2015C238）

薛文奎（1979 -），男，河南驻马店人，讲师，硕士，研究方向为计算流体动力学分析和机器人技术。