双容水箱快速无超调切换控制
2017-04-27唐予军
王 霞,侯 阔,唐予军
(1.河北大学 电子信息工程学院,保定 071002;2.河北省数字医疗重点实验室,保定 071002)
双容水箱快速无超调切换控制
王 霞1,2,侯 阔1,唐予军1
(1.河北大学 电子信息工程学院,保定 071002;2.河北省数字医疗重点实验室,保定 071002)
基于物质量观点为双容水箱设计无超调的快速响应切换控制器。首先,由水箱的静态工作点得到其平衡流形。然后,设计工作点迁移控制器、工作点保持控制器以及两个控制器的切换律从而得到液位的切换控制器。所设计的切换控制器从理论上严格保证系统无超调特性。仿真和实验同时验证了所得结果的正确性和有效性。
基于物质量的切换控制;快速无超调;双容水箱
0 引言
双容系统在人们的生活、生产中应用非常广泛,工业上许多的多输入多输出被控对象的整体或局部都可以抽象成双容系统,如水箱[1]、锅炉[2]、发动机[3]等。因此,双容系统的控制实验研究具有很高的研究价值。由于两个容量的存在和相互作用,使得双容系统的控制比较困难,主要表现在响应快速性和动态精度不能兼顾。这主要是因为两个容量的存在造成了被控输出对控制输入作用响应的滞后,控制输入的高频成分难以通过被控输出观察。若控制量变化迅速,很容易造成系统过度或欠量储物,将来反应到输出端就形成了超调和欠调[4]。超调往往会造成能源的浪费或引发安全问题,因此在一些需要避免超调出现的场合,一般采用缓慢调节的方法,避免双容系统过度储物,这势必要牺牲系统的响应快速性。串级控制是改善控制过程品质极为有效的方法,并得到了广泛的应用,但是仍然无法从理论上严格保证无超调[5]。最优控制高级控制策略可以获得更为优良的动态性能,但是需要被控过程的数学模型。对很多复杂过程而言,获得较为精确的数学模型是个费时费力的庞大工程[6]。许多双容系统过程非线性特性显著,整体的动态模型难以获得。在没有数学模型的情况下,设计兼顾快速性和动态精度的系统控制器具有实际意义和理论挑战性,这方面的研究鲜见报道。
相对于单一控制器而言,多个控制器切换控制为设计者提供了更多的自由度,从而可能获得单一控制所不可能达到的控制效果。如广为应用的变结构控制[7],多模型自适应控制[8]等方法都是通过多个控制器的切换提高了系统的抗扰动能力和动态性能。多控制器切换使得整个闭环系统成为一个切换系统,可以应用切换系统理论[9]加以分析和论证。近10年来,切换系统理论迅速发展,形成了较系统的理论体系主要利用类Lyapunov函数方法[10]进行分析和设计。大量结果表明,通过切换信号和控制器的双重设计,可以获得非切换系统所不具有的优良性能。
物质量在控制中一直扮演一个重要的角色。双容系统调节的过程相当于改变系统状态从一个平衡工作点到另一个工作点,这与物质量密切相关。这个过程大约需要两个阶段,储能阶段和建立新的平衡阶段。前一个是从原始水平到目标水平改变系统物质量,后一个是在新的平衡工作点满足物质量耗散率然后建立一个新的动态平衡的物质量。瞬态性能也可以从物质量的角度解释。很明显,物质量增加越快,被控量提升的越快。然而,快速增加被控量往往储存过多的物质量,可能会导致超调,这是稳定性考虑中的不良因素。关键问题是什么时候切换控制器,切换时间和主控制器的输出对超调有很大的影响。因为超调只有在系统物质量超过目标操作点的物质量时才出现,我们希望通过避免物质量过度存储来保证超调响应,这是我们工作的基本动机。
本文为双容水箱设计了一种切换控制器,所设计的极限控制器和积分控制器在基于物质量的控制策略下交替作用于系统,确保液位的快速无超调调节。本文的结果特点在于:1)从理论上严格保证了液位的无超调特性;2)不需要对象精确的动态数学模型,只需要水槽的平衡工作点的信息。实验和仿真验证了切换控制策略的有效性。
1 问题描述
双水箱结构如图1所示[11]。

图1 双容水箱结构图
u为进水量,A1、A2分别为上下水箱底面积,Ku为进水阀门液阻,K1为上水箱出水阀门液阻,K2为下水箱出水阀门液阻,h1为上水箱液位,h2位下水箱液位,hr为下水箱液位设定值。
根据物质量平衡关系——单位时间内被控过程流入量与流出量之差等于被控过程内部存储量的变化率,可以得出:

本文的控制目标是为双容水箱(1)、(2)设计切换控制器和切换律,使得对任意设定液位高度h2r,下水箱液位h2满足:
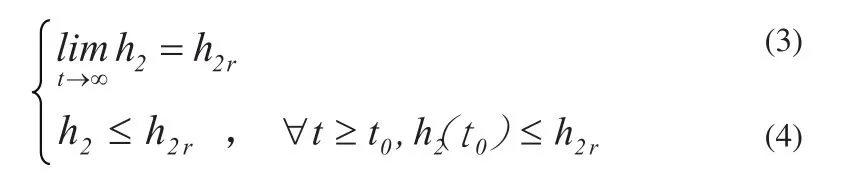
2 控制器设计
双容水箱超调监管任务之所以变得复杂,是因为下水箱液位影响因素不仅来源于阀门开度,而且来源于上水箱液位。传统上,避免超调是以牺牲速度为代价的。怎样同时确保速度和超调从理论到实践都是一个长期需要讨论的难题。这一节首先讨论了平衡流形的意义以及它和液位调节的关系,在物质量的观点上分析了影响快速性能的因素。然后讨论怎么无超调调节下水箱液位,在一个基于物质量的切换规则下同时给出极限控制器和积分控制器。最后,从理论上分析快速性和无超调性能。
2.1 平衡流形
平衡流形就是水箱稳定工作点的集合。一个特定的下水箱液位或者特定的系统物质量,可以确定一个唯一的水箱稳定工作点。因此,对于一个双容水箱,如果下水箱液位保持常量或者渐渐的接近一个常量,系统状态会渐渐的接近一个有同样下水箱液位相应的平衡点。同样的,系统物质量保持不变或者接近一个常量保证了系统状态接近一个有同样物质量水平的平衡点。在平衡操作点,液位高度保持不变。换言之,在平衡操作点储存的物质量是不变的,所以水箱进入的物质量和流出的物质量是相等的。因为平衡流形是所有平衡操作点的集合,在平衡流形上的每个点代表了物质量平衡状态。
调节液位h2从一个稳定值h20到设定值h2r本质上相当于改变平衡操作点。在两个稳定工作点中间有一个动态过程,系统状态会首先从点(h10,h20)离开平衡流形,然后在目标点(h1r,h2r)回到平衡流形。从物质量的观点看,水箱需要储存物质量来改变液位,因此物质量平衡必须被破坏,也就是说,系统状态必须离开平衡流形。为了在目标值保持液位,必须要建立一个新的物质量平衡,所以系统状态必须返回到平衡流形。像引言中说的那样,液位调节过程包括两个阶段,储存物质量过程和建立新的平衡过程。控制性能取决于这两个阶段。物质量存储的越快,液位增加的越快。如果系统物质量不超过在建立平衡阶段目标操作点的物质量,液位就不会超过它的目标值,也就是说,不会有超调出现。
如图2所示,虚线是平衡流形。在平衡流形上A和B两个点是不同的平衡工作点(h1A,h2A,uA)和(h1B,h2B,uB),u为阀门开度。B点比A点的液位高,这就意味着B点的物质量水平比A高。

图2 调液位状态轨迹
图2中曲线A→B是一个液位h2从h2A到h2B的升高过程(曲线B→A是一个液位h2从h2B到h2A的下降过程)。在这个过程,系统物质量从EA增加到EB(从EB减少到EA)。使用平衡流形可以建立液位和系统物质量之间的映射,所以液位调节问题可以转变成物质量控制问题,这就是基于物质量转换控制的基础。
2.2 基于物质量的切换规则
控制系统的性能集中体现在其阶跃响应上。实际应用中,大部分控制指令也是要求对象工作状态在不同的工作点间转换。双容水箱从一个稳态工作点到另一个稳态工作点的迁移可以分为两个过程,储存物质量过程和建立动态平衡两个过程。第一个过程决定了系统响应的快速性,物质量的存储速度,控制的主要任务是使系统流入、流出量不平衡最大化。当物质量的存储达到预定水平,需要及时进入第二个过程:在新的工作点建立新的流入、流出平衡关系。第一阶段物质量的过量和欠量存储将导致的系统动态中出现超调和欠调。由于两个过程的主要任务不同,设计两个控制器更为合适:存储(极限)控制器和平衡(积分)控制器。两个控制器切换时机的选择尤为关键,会直接影响系统物质量的存储得是否过量(欠量),进而影响动态特性。根据双容水箱特点,依据系统物质量存储状态设计切换逻辑可以得到兼顾快速性和动态性能的控制器,在不依赖数学模型的情况下解决响应快速性和超调的矛盾。通过之前对平衡流形的分析,在平衡流形有一个唯一的点符合目标液位,可以计算目标平衡点液位的体积。因此,通过平衡流形可以建立目标液位和目标体积之间的关系。如果实际体积和目标体积保持相等,即。系统状态将接近目标的平衡,因此液位会接近目标液位。
控制器程序流程图如图3所示,V0为液体实际体积,h0为实际液位,umax为最大进水量,ur为切换时刻进水量,Vr为目标体积。为了使液位以最快的速度升高,当实际液位值小于设定液位值时,阀门开度为最大。即流入流出量不平衡最大化,系统会以最快的速度存储物质量。

图3 控制器流程图
设计切换控制器如下:

如果切换时间选取h2=h2r,超调就可能会出现。这是因为当h2=h2r的时候,h1的响应速度比h2快,h1比h1r大。因为超调只有在系统物质量超过目标操作点物质量时才出现,当V(ts)=Vr时的时间ts作为切换时间,对于所有t≥ts,能够保证V(ts)=Vr。即当实际的上水箱液位和下水箱液位体积之和等于目标的上水箱液位和下水箱液位体积之和时,阀门开度切换到目标液位对应的阀门开度。同时在切换时刻,根据系统的当前消耗重置积分器状态,将PID的积分器的初始值重置为0。
图4定性地显示了切换控制器造成的状态轨迹,其中曲线ACB表示一个液位升高过程,曲线BDA表示一个液位下降过程。阀门开度u视为平衡流形的参数变化量。通过图3的切换逻辑,阀门开度在A→B (B→A)增加(减少)去储存(耗散)物质量。因为上水箱液位响应速度比下水箱液位快,状态轨迹从上面(下面)离开平衡流形。直到状态轨迹遇到目标物质量水平线点C(D),然后切换到积分控制器,重置积分状态。这里分析了液位升高过程,和液位降低过程类似。

图4 基于物质量的切换法则和重置机制时调节液位的状态轨迹
定理:针对双容水箱系统式(1)、式(2),如果采用控制律式(5)、式(6),则实现控制目标式(3)、式(4)。
证明:
1)储能阶段
当u=umax时,物质量以最快速度储存。
2)建立新平衡阶段
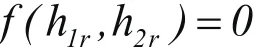
即h1r,h2r是其平衡点。
构造一个正定函数:


3 实验与仿真
为了验证我们方法的有效性,使用Simulink仿真和罗克韦尔设备进行实验,通过和传统的串级控制方法对比展示了基于物质量切换控制方法的优势。
3.1 仿真
表1和表2分别给出了水箱模型参数和控制器参数,对模型分别进行串级控制和切换控制实验,通过经验试凑法获得表2中最优PID参数,通过表1数据计算出表2中目标体积Vr。

表1 仿真控制对象参数

表2 仿真控制器参数
图5为仿真结果,红色线代表切换控制,黑色线代表串级控制。通过对比可以看出,串级控制存在明显的超调现象,而切换控制不仅能快速达到下水箱液位设定高度,而且实现了严格无超调。
3.2 实验
本实验设计的总体结构框架如图6所示。通过以太网将上位机电脑和控制器相连接,由电脑上的界面监控系统运行并发出指令。再将控制器的输出节点与执行器中的电动调节阀相连,通过控制网连接系统的被控对象——实验水箱,将控制器的输入节点与水箱中的液位变送器相连,从而起到控制和监控作用。
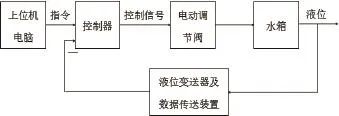
图6 水箱液位控制系统总体结构框架图
实验水箱整体装置图如图7所示。右边背板上依次为电源、控制器、通信模块和I/O模块。中间是上位机和操作台,面板上可以实时观测水箱液位高度。左边为实验水箱、电动阀门和传感器检测变送设备。整个过程控制系统的构建分为网络连接搭建和硬件电气连接搭建,本设计采用了NetLinx网络构架进行网络连接,将控制器、上位机和实验水箱三者连接为一个系统。
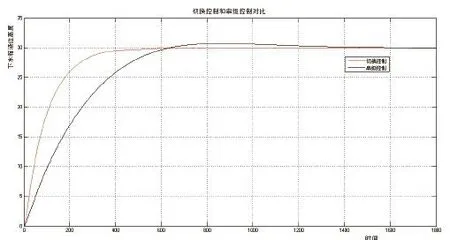
图5 切换控制和串级控制仿真对比

图7 实验水箱整体装置图
图8记录了实验过程中上下水箱的物质量变化,由图可以看出,物质量储存阶段,上水箱物质量迅速增加,下水箱物质量几乎不变。建立平衡阶段,上水箱物质量减少,下水箱物质量增加,物质量没有过度存储,所以下水箱液位没有超调,实验中下水箱液位变化如图9所示。

图8 上下水箱物质量变化
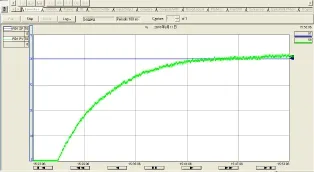
图9 下水箱液位
4 结论
本文研究了双容水箱的切换控制问题,通过多个控制器的切换提高了多容过程闭环响应的快速性和精确性,从理论上保证实现无超调的快速响应。
本文研究成果对所有的双容系统均可适用,从物质量存储角度提出新的控制思路和方法。所设计的控制器将极大程度地缓解快速性和动态精度的矛盾,大幅度提高双容系统的控制精度和响应速度,为生产工艺进一步提高奠定基础。
[1] 杨旭,周悦,于广平.水箱液位控制系统的研究与设计[J].制造业自动化,2011,33(8):128-130.
[2] 唐国泽,李鹏,任文萍,等.自然循环锅炉控制系统半实物仿真平台设计[J].控制工程,2016,23(6):93:3-936.
[3] 王耀南,申永鹏,孟步敏,等.车用汽油发动机电子控制系统研究现状与展望[J].控制理论与应用,2015:32(4):432-447.
[4] 陈小平,徐红兵.一类非线性系统的无超调控制[J].控制与决策,2013,28(4):627-631.
[5] 周荣强,罗真.双容水箱液位DMC-PID串级控制仿真研究[J].自动化仪表,2011,32(10):63-65.
[6] 张吉烈,张化光,罗艳红,等.基于广义模糊双曲模型的自适应动态规划最优控制设计[J].自动化学报,2013,39(2):142-149.
[7] 张彩虹,刘云龙,高存臣,等.基于隐Lyapunov函数的软变结构控制: 一种控制策略[J].控制与决策,2012,27(1):71-76.
[8] 张维存,刘冀伟,胡广大.鲁棒多模型自适应控制系统的稳定性[J].自动化学报,2015,41(1):113-121.
[9] 肖慧敏,赵林,王春花.不确定时滞切换系统的鲁棒滑模控制[J].控制理论与应用,2011,28(11):1621-1626.
[10] 陈征,高岩.切换系统的二类共同Lyapunov函数[J].控制与决策,2013,28(4):623-631.
[11] 李国勇,何小刚,阎高伟.过程控制系统[M].北京:电子工业出版社,2015.
Fast noovershoot switching control for double tanks
WANG Xia1,2, HOU Kuo1, TANG Yu-jun1
TP273
A
1009-0134(2017)04-0030-05
2017-01-01
国家自然科学基金(61403118,11271106);河北省自然科学基金(F2015201088),河北大学科研基金资助项目(2010Q04);河北大学中西部提升综合实力-高层次人才培养和引进计划项目
王霞(1978 -),女,河北唐山人,副教授,博士,主要从事切换系统研究。
