Schwarz-Pick引理的推广
2017-04-25杜美容
杜美容, 卢 金
(湖州师范学院 理学院, 浙江 湖州 313000)
Schwarz-Pick引理的推广
杜美容, 卢 金
(湖州师范学院 理学院, 浙江 湖州 313000)
利用Schwarz引理和单位圆盘自同构,并结合系数估计,通过二阶、三阶求导,给出单位圆盘上全纯函数的Schwarz-Pick引理的高阶推广.
Schwarz-Pick引理; Schwarz引理; 全纯函数
MSC 2010:30C10
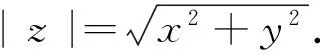
定义1[1-3]设f是单位圆盘D上的函数.若z∈D,f在z处可微,则称f为D上的全纯函数.若z,w∈D,当z≠w时,有f(z)≠f(w),则称f在D上是单叶的.若f是D上的单叶全纯函数,且f(D)=D,则称f是D上的一个全纯自同构,D上全纯自同构的全体记为Aut(D).单位圆盘的自同构具有如下形式:
式中:a为单位圆盘内的点;θ为实数.
Schwarz在1885年提出了Schwarz引理,得到了单复变中重要的Riemann映射定理.Pick在1915年将Schwarz引理推广到更一般的形式,得到了Schwarz-Pick引理.
Schwarz-Pick引理[1]设f为D到D内的全纯映射,则
∀z∈D.
文献[4-7] 给出了f(z)高阶导数估计,也可认为是Schwarz-Pick引理的推广.本文运用Schwarz引理和单位圆盘自同构,得到了与之前不同的二阶和三阶估计.
1 主要结果
首先,本文运用两个基本引理刻画二阶和三阶导数,其中引理2是系数关系.
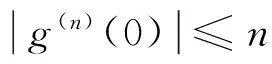
引理2 设g为D到D内的全纯函数,且g(z)=a1z+a2z2+a3z3+…则
定理1 设f为D到D内的全纯函数,则
∀z∈D,
且该估计是精确的.
证明 取定z0∈D,设f(z0)=w0,则令f=ψw0∘g∘φz0,其中:
g为D到D内的全纯函数,且g(0)=0.
由于g(0)=0,即令g(z)=a1z+a2z2+a3z3+…则g′(0)=a1,g″(0)=2a2,记f1=g∘φz0,得:
再考虑f=ψ∘f1,其中:
则可得:
由引理2,带入系数关系,


故对任意的z∈D,有:
该估计是精确的,取g(z)=z,则
f1(z)=g(φz0(z))=φz0(z),f(z)=ψw0(f1(z))=ψw0(φz0(z)),
于是
证毕.
定理2 设f为D到D内的全纯函数,则
证明 设a∈D,令g(z)=φf(a)[f(φa(z))],其中:
于是有:
则
当z=0时,有:
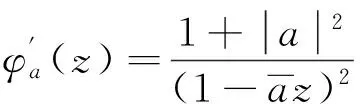
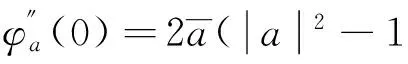
类似地,可以得到:
于是
故
那么
等式两边取绝对值,得:
又由a,z的任意性,则
∀z∈D.
证毕.
定理3 设f为D到D内全纯函数,则
证明 令g(z)=φf(a)[f(φa(z))],其中:
则有:
且
求三次导数得:

当z=0时,
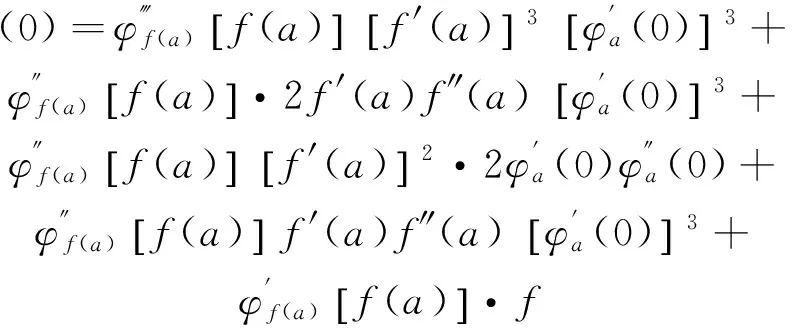
(1)

则
(2)
类似地,可以得到:
那么
(3)

因此有:
(4)
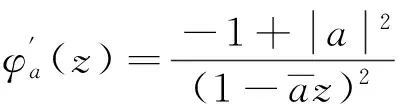
则
(5)
类似地,可以得到:
于是
(6)
故
则
也即
(7)

即
(8)
类似地,可得到:
故
(9)
将(2)式~(9)式代入(1)式,得:
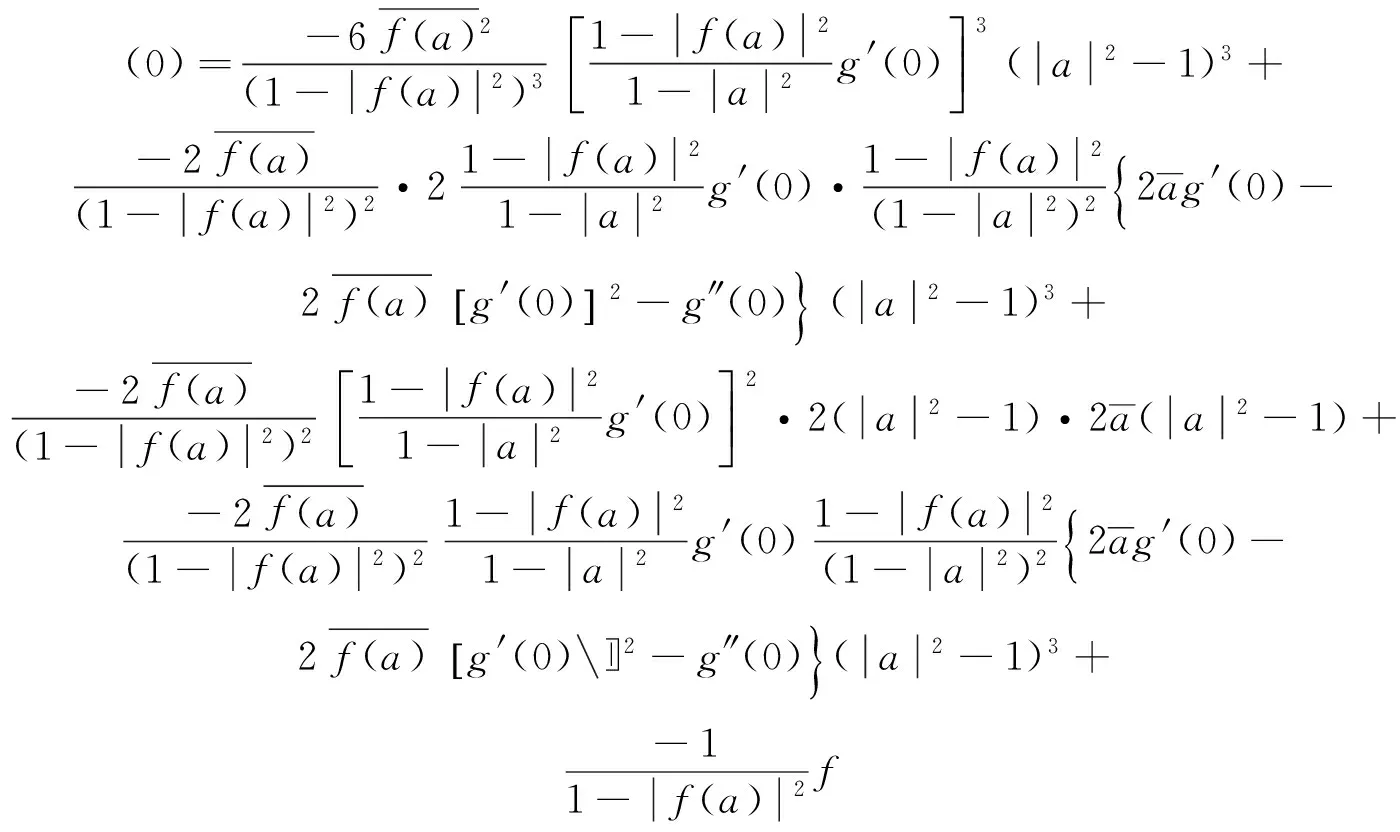
于是
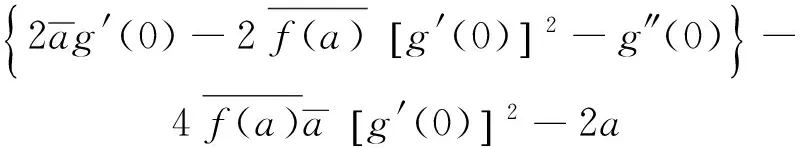
即
则
‴
等式两边取绝对值,得:
(10)
由引理1知:
代入(10)式,可得:
又由a,z的任意性,则
∀z∈D.
证毕.
[1]史济怀,刘太顺.复变函数[M].合肥:中国科学技术大学出版社,1998.
[2]龚升.简明复分析[M].北京:北京大学出版社,1999.
[3]龚升.关于Mobius变换的一点注记[J].纯粹数学与应用数学,1985,1(1):1-15.
[4]潘一飞,廖孝中.关于有界函数的导数[J].江西师范大学学报,1984(1):21-24.
[5]苑文法.有界正则函数的导数估计[J].数学杂志,2001,21(3):301-303.
[6]戴绍虞,潘一飞.有界解析函数n阶导数的估计[J].数学杂志,2010,30(2):296-302.
[7]DAISY,PANYF.NoteonSchwarz-Pickestimatesforboundedandpositiverealpartanalyticfunctions[J].ProcAmerMathSoc,2008,136(2):635-640.
MSC 2010:30C10
[责任编辑 高俊娥]
The Generalization of Schwarz-Pick Lemm
DU Meirong, LU Jin
(School of Science, Huzhou University, Huzhou 313000, China)
In this paper, using Schwarz lemma and automorphism of unit disk, combining the estimation of coefficient, we obtain the generalization of holomorphic function's Schwarz-Pick lemma to higher-order derivatives with the second and third differentiations in the unit disk.
Schwarz Lemma; Schwarz-Pick Lemma; holomorphic function
2016-10-23
国家自然科学基金项目(11501198);浙江省自然科学基金项目(LY16A010012);湖州师范学院“大学生创新创业训练计划”项目(2016-112).
卢金,讲师,研究方向:多复分析.E-mail:luking@zjhu.edu.cn.
O174.5
A
1009-1734(2017)02-0001-07
