短视型和策略型消费者的商场服装动态定价研究

肖胜昔

(湖州职业技术学院 商贸与经管学院，浙江 湖州 313000)

短视型和策略型消费者的商场服装动态定价研究

肖胜昔

(湖州职业技术学院 商贸与经管学院，浙江 湖州 313000)

从心理学的角度分析策略型和短视型消费者的购买决策过程，根据服装消费者临界估价和估价分布特征估算服装的期望购买人数，建立商场服装动态定价目标函数，并求解二阶段最优价格路径.通过实例研究策略型消费者的比例对商场最优定价及收益的影响.结果得出：策略型消费者比例与第一阶段期望利润和总期望利润呈负相关，与第二阶段期望利润呈正相关；策略型消费者比例与两阶段最优定价呈正相关，与两阶段的降价幅度呈负相关.

动态定价； 短视型消费者； 策略型消费者

0 引 言

在服装零售商场，销售商常常会遇到两种消费者：一种是只要他们的支付意愿高于服装产品定价，就会购买；另一种是他们的支付意愿高于产品定价，但拒绝现在购买，因为他们会考虑产品将来会降价.前者为短视型消费者，后者为策略型消费者.在消费者行为研究方面，Muth(1962)首次提出了消费者的策略行为概念，认为凭借对零售商运营策略的深刻理解和准确把握，消费者可以采取使自己收益尽量大的购买行为[1]；Coase(1972)研究了零售商针对消费者策略行为时的定价问题，认为在面临消费者冷静等待产品降价时，他们也被迫按边际成本定价[2]；Elmaghraby(2003)认为不同消费者对厂商定价的响应特征是不同的，短视型消费者是只要厂商定价不高于他们的支付意愿就会购买，而策略型消费者是即使他们的支付意愿高于厂商定价也会考虑产品未来降价情形而拒绝购买[3]；Tang(2010)认为策略型消费者的决策准则是只有在以当期价格购买获得的收益大于将来以另一种价格购买所获得的收益时他们才会购买[4].在厂商定价研究方面，Elmaghraby 等(2008)创建了一个针对策略型消费者的定价模型，该模型以顾客估价为条件，分别研究了在完全信息和不完全信息下厂商的最优定价[5]；Su(2010)从估价和耐心两个维度将消费者分为四类，并认为消费者的估价和耐心共同决定了商品的价格路径[6]；Moorthy研究了厂商与策略型顾客之间的两阶段价格博弈，博弈结果是厂商价格会随时间降低[7].在国内，杨慧等在研究消费者购买决策过程时提出了“临界估价”的概念，并提出了可根据“临界估价”和顾客估价分布特征估算已购物顾客人数的研究方法[8]；曾贺奇还进一步研究了短视型和策略型消费者并存下替代性产品的动态定价模型[9].

可见，学者们的研究大多集中在策略型消费者的行为特征、决策准则以及相应的厂商定价上.然而商场服装消费者是短视型顾客和策略型顾客的混合体，服装产品的个性化特点决定了其销售周期短以及消费者的估价呈均匀分布，这些都对商场服装定价产生特殊的影响.目前尚没有模型针对服装消费者及行业的特点来研究商场服装动态定价问题.

1 模型描述与决策过程分析

1.1 符号设置和前提假设

商场在服装销售周期内向消费者销售某种服装，销售前期按全价销售，销售后期实行降价促销.整个销售期间服装足量供应，销售期结束时服装全部从商场撤出.模型涉及到的主要符号和前提假设为：

(1) 分为两个销售阶段：第一阶段的销售价格用ρ1表示；第二阶段的销售价格用ρ2表示，且ρ1>ρ2.

(2) 因为在某个区域销售服装，其目标顾客数量是相对固定，记为N.服装的流行性决定了必然存在紧追时尚的短视型顾客，而服装市场上激烈的竞争导致经常性的降价促销，由此也产生了相对数量的策略型顾客.设策略型消费者所占比例为λ(0<λ<1)，则短视型消费者所占比例为1-λ.消费者一般不会重复购买同一服装，故假设每个消费者只能购买一个单位的服装产品.

(3) 服装产品总量为Z，且Z>N.

(4) 不同的消费者由于主客观原因对同一服装的估价都不相同，具有随机性，故可假设消费者对服装的估价在(0，M)上呈均匀分布.

(5) 服装产品的单位成本为c.

(6) 由于收益具有时间价值，模型对第二阶段的消费者和商场的收益都作了贴现处理，且贴现因子为θ(0<θ<1).

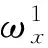
1.2 消费者决策过程分析和最优定价目标函数构建

由于服装消费者估价具有差异性和随机性，故购买服装的消费者对服装的估价有高有低，呈均匀分布.其中一定存在对产品估价最低的消费者，这个最低估价即已购买服装消费者集合的临界估价[8].依据这个定义，在对产品有需求且对产品满意的消费者集合中，如果某个消费者的估价高于临界估价，他就会购买产品.因此，可以根据服装消费者估价均匀分布的特征和服装消费者集合的临界估价来估算服装的购买人数.由于商场服装的定价大小直接影响消费者集合的中临界估价大小，故本文从商场服装定价及其对服装消费者集合中临界估价的影响出发，分析两种类型消费者两阶段的购买人数，并据此构建最优化定价目标函数.

1.2.1 第一阶段

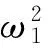
M1-ρ1=θ(M1-ρ2).

(1)

(2)

1.2.2 第二阶段

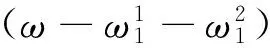
(3)

商场服装的最优定价目标是φ1和φ2之和的最大化，如下式所示：

(4)

2 商场服装最优化价格路径

2.1 第二阶段

(5)

2.2 第一阶段

在第一阶段开始时，商场决定ρ1.针对商场定价ρ1，不同的消费者由于其保留估价和决策规则不同，故购买决策也不相同.短视型消费者的购买决策只与ρ1有关，而策略型消费者购买前要比较第一阶段的消费者剩余与第二阶段的消费者剩余.所以，策略型消费者的购买决策不但与ρ1有关，而且与ρ2有关.商场在第一阶段确定ρ1后就可根据(5)式推断第二阶段的最优化定价ρ2，同时也能知道策略型消费者的决策准则，即当他们的保留估价高于(1)式中的临界估价Μ1时，他们就会购买服装.由(1)式和(5)式可得：

(6)

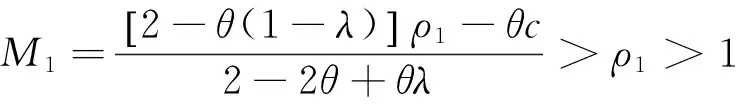
2.3 最优价格路径求解

将(5)式代入(3)式得：

(7)

(8)

商场在短视型顾客和策略型顾客并存的情况下实行二阶段动态定价，如果得知策略型顾客的比例为λ(0<λ<1)，则商场最优化定价为：

其中：

β=8-4λ-(18-20λ+4λ2)θ+(13-23λ+10λ2-λ3)θ2-(3-7λ+5λ2-λ3)θ3；

μ=12-4λ-(26-24λ+4λ2)θ+(17-27λ+11λ2-λ3)θ2-(3-7λ+5λ2-λ3)θ3.

下面根据上述结论检验最优定价模型的假设：

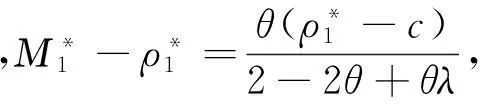
3 动态定价模型的实例分析

下面通过实例探讨他们之间的关系.

假设某商场销售一款服装，服装单位成本为600元，总量1 200件，消费者最高估价为2 000元，对该服装满意且有购买意向的消费者人数为1 000人，策略型消费者比例为0.5，贴现因子为0.6，即M=2 000，C=600，λ=0.5，θ=0.6，则两阶段的最优价格为：

两阶段的总收入为：

φ*

可见，商场在服装销售两阶段的最优定价是：第一阶段女装定价为1 151.80元，第二阶段服装定价为951.15元，商场在第一阶段销售服装期望利润为192 498.19元，在第二阶段销售服装期望利润为36 990.84元，商场销售服装的总期望利润为299 489.03元.为了探讨策略型消费者比例λ对企业定价策略及收益的影响，本文给出了不同λ值下的各阶段最优定价、降价幅度、各阶段期望利润及总期望利润等数据.由于收益具有时间价值，故第二阶段的利润需进行贴现处理，即总期望利润φ*={φ1+θφ2}，各类数据如表1所示.

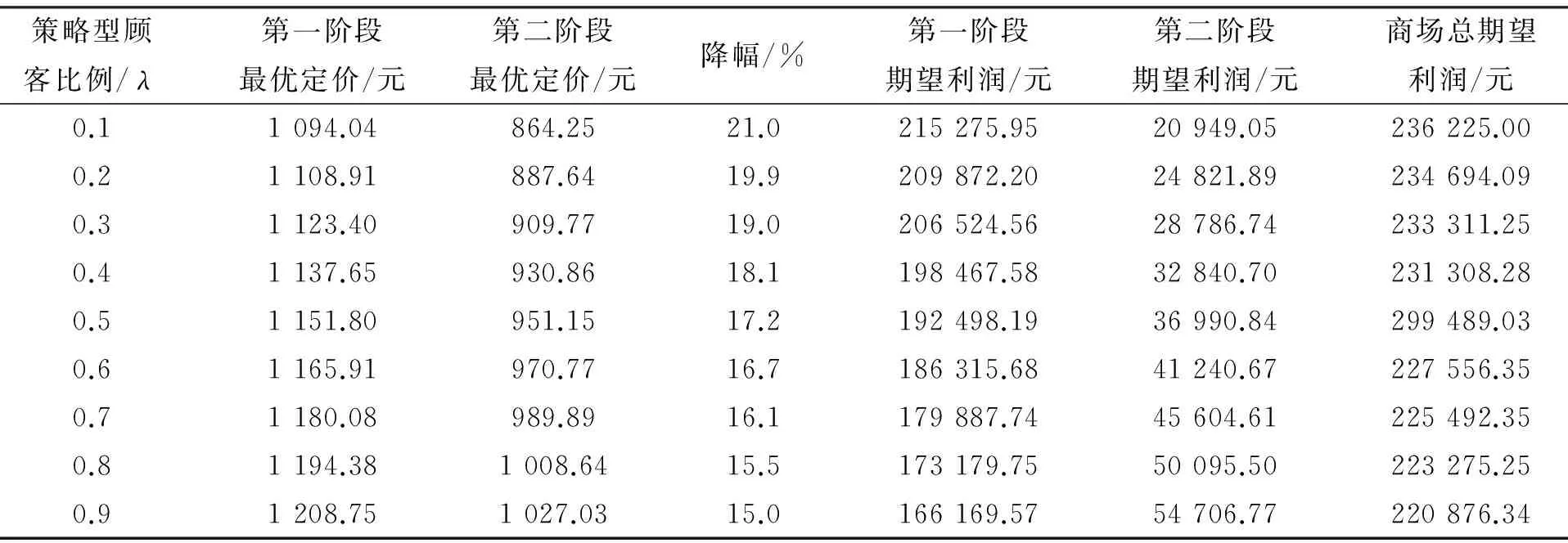
表1 不同λ值下的动态定价、期望利润

Table 1 Dynamic pricing and expected profit under different values ofλ

策略型顾客比例/λ第一阶段最优定价/元第二阶段最优定价/元降幅/%第一阶段期望利润/元第二阶段期望利润/元商场总期望利润/元0.11094.04864.2521.0215275.9520949.05236225.000.21108.91887.6419.9209872.2024821.89234694.090.31123.40909.7719.0206524.5628786.74233311.250.41137.65930.8618.1198467.5832840.70231308.280.51151.80951.1517.2192498.1936990.84299489.030.61165.91970.7716.7186315.6841240.67227556.350.71180.08989.8916.1179887.7445604.61225492.350.81194.381008.6415.5173179.7550095.50223275.250.91208.751027.0315.0166169.5754706.77220876.34

通过分析表1得出：

(1) 策略型消费者比例与第一阶段期望利润和总期望利润呈负相关，而与第二阶段期望利润呈正相关.

从表1中看出，随着λ从0.1增加到0.9，商场第一阶段的利润从215 275.95元下降到166 169.57元，商场第二阶段的利润从20 949.05增加到54 706.77元，商场总的期望利润从236 225.00元下降到220 876.34元.其原因在于：随着λ值的增加，策略型消费者越来越多，他们在第一阶段服装价格较高时选择等待，而在第二阶段服装降价后才出手购买.所以商场第一阶段的期望利润由于购买人数减少而降低，而第二阶段的期望利润则由于购买人数增加而上升.此外，随着λ值的增加，更多比例的消费者是在商场实行降价的第二阶段购买服装，拉低了两个阶段的服装平均售价，所以商场总的期望利润也随之降低.由此可见，弄清各类消费者比例是实现二阶段最优化定价的必要条件.

(2) 策略型消费者比例与两阶段最优定价呈正相关，与两阶段的降价幅度呈负相关.

从表1中看出，随着λ从0.1增加到0.9时，商场在第一阶段的最优定价由1 094.04元提高到1 208.75元，商场在第二阶段的最优定价由864.25元提高到1 027.03元，而商场服装在两阶段的降价幅度从21%元下降到15%.其原因在于：当λ较小时，短视型顾客多而策略型顾客少，总的购买人数较多.商场在第一阶段最优定价较低，意味着顾客的临界估价较低，导致较多的购买者在第一阶段购买服装.而在第二阶段降价幅度大，意味着第二阶段顾客的临界估价较低，也促使较多的剩余消费者在第二阶段购买服装，从而获得尽可能多的总期望利润.当λ逐渐增大时，短视型顾客少而策略型顾客多，而总的购买人数在减少.商场在两阶段的最优定价都较高，可使人数有限的购买者在两个阶段都以较高的价格购买服装，获取较高的人均利润.而商场在第二阶段降价幅度小，可使策略型顾客对等待大幅降价以获取更多的消费者剩余的预期下降，从而使其尽早购买服装.

4 结 论

本文研究了在策略型消费者和短视型消费者并存的情况下，如何对商场服装进行动态定价的问题.通过对模型的部分假设进行论证，使之符合服装零售行业实际，保证了模型的实际应用价值，并根据服装消费者临界估价和估价分布特征估算两类消费者二阶段的期望购买人数，建立二阶段动态定价目标函数，求解出商场的二阶段最优价格路径.还通过实例分析得出：当商场的策略型顾客较少时，商场服装在两阶段的定价都应较低，且两阶段降幅也较大，这样商场可获得较高的总期望利润；反之，当商场的策略型顾客较多时，商场服装在两阶段定价要适当高些，且两阶段降幅要小些，以获得较高的人均利润.本文没有考虑策略型消费者对未来服装可获得性的估计具有不确定性的情况，这会影响消费者的购买行为，从而影响最优价格的设计，这是今后需要继续研究的方向.

[1]MUTHJF.Rationalexpectationsandthetheoryofpricemovements[J].Econometrica,1961,29(3):315-335.

[2]COASERH.Durabilityandmonopoly[J].JournalofLawandEconomics，1972，15(1)：143-149 .

[3]ELMAGHRABYW,KESKINOCAKP.Dynamicpricinginthepresentofinventoryconsiderations:researchoverview,currentpracticesandfuturedirections[J].ManagementScience,2003,49(10):1 287-1 309.

[4]TANGCS.Areviewofmarketing-operationsinterfacemodels:fromco-existencetocoordinationandcollaboration[J].InternationalJournalofProductionEconomics,2010,125(1):22-40.

[5]ELMAGHRABYW,GÜLCÜA,KESKINOCAKP.Designingoptimalpreannouncedmarkdownsinthepresenceofrationalcustomerswithmultiunitdemands[J].Manufacturing&ServiceOperationsManagement,2008,10(1):126-148.

[6]SUX.Intertemporalpricingwithstrategiccustomerbehavior[J].ManagementScience,2007,53(5)：726-741.

[7]MOORHYKS.ConsumerExpectationsandthePricingofDurables[M].Lexington:LexingtonBooks，1988.

[8]杨慧,周晶.考虑消费者短视和策略行为的动态定价研究[J].管理工程学报,2010，24(4)：133-137.

[9]曾贺奇，张玉林.短视型和策略型消费者并存下的替代性产品跨期定价[J].系统工程,2015,5(33)：33-39.

[责任编辑 高俊娥]

A Research on Dynamic Pricing of Shopping Mall Clothing of Myopic and Strategic Consumers

XIAO Shengxi

(School of Business and Economics， Huzhou Vocational and Technical College， Huzhou 313000， China)

From the perspective of consumer psychology, this paper analyzes the process of strategic and myopic consumer purchase decision, estimating the number of women's expected purchases according to the distribution characteristics of the critical valuation and valuation. On this basis, this paper establishes the dynamic pricing objective function of ladies, and solves the two stage optimal price path. In addition, we also study the effect of the proportion of strategic consumers on the optimal pricing and revenue of the shopping malls. The results show that the proportion of strategic consumers is negatively correlated with the expected profit and the total expected profit, and is positively correlated with the second stage expected profit, and the proportion of strategic consumers is positively correlated with the two stage.

dynamic pricing; myopic consumers; strategic consumers

2016-12-10

肖胜昔，讲师，研究方向：市场营销学.E-mail:1376872402@qq.com

F270.5

A

1009-1734(2017)02-088-06