双参数指数分布的兴趣参数的广义置信区间

袁守成

(普洱学院 数学与统计学院，云南 普洱665000)

双参数指数分布的兴趣参数的广义置信区间

袁守成

(普洱学院 数学与统计学院，云南 普洱665000)

研究了双参数指数分布的分位数和可靠度函数的广义置信区间问题.首先利用广义枢轴量给出2个兴趣参数的广义置信区间，并证明了在频率意义下2个兴趣参数的广义置信区间具有实际的置信水平，最后通过实例对上述方法进行了数值模拟，结果验证了该方法的有效性.

双参数指数分布； 广义置信区间； 广义枢轴量； Fiducial模型

双参数指数分布是一类应用非常广泛的分布，常常用于产品寿命的可靠性分析中，也用于各种经济模型和工程技术问题中.Epstein[1]指出对于有瑕疵的材料，其强度服从双参数指数分布；Easterling[2]建立的关于蒸汽发生器的模型是基于双指数分布测量误差的假定上的；Bain等[3]在研究水文站的洪水资料时也是利用2个独立的双参数指数分布的变量之差生成双参数指数分布.因此，双参数指数分布在许多领域都有着广泛的应用.对双参数指数分布的兴趣参数的置信区间的研究从未停止，研究者们提出过很多方法，比如基于参数的最优线性同变估计、最优线性无偏估计和最大似然估计等方法确定未知参数的精确置信区间；采用条件分布的方法给出了兴趣参数的置信区间[4].Engelhardt等[5]在产品的可靠寿命问题中，给出了兴趣参数的近似置信下限，但由于计算方法过于复杂而不便于使用.笔者运用Weemhandi[6]提出的广义枢轴量方法，给出了双参数指数分布分位数和可靠度函数的精确置信区间，该方法解决了在求参数置信区间时，由于讨厌参数和兴趣参数同时存在，难以获得兴趣参数的精确置信区间的问题.

设R=r(X;x,ξ)是X,x,ξ的函数，其中ξ=(θ,η)，若R满足性质:

1)R的分布与ξ=(θ,η)无关；

2)R的观测值robs=r(x;x,ξ)不依赖于讨厌参数η；

1 双参数指数分布兴趣参数的广义置信区间

设随机变量X服从双参数指数分布，其密度函数为

f(x;μ,σ)=σ-1exp(-(x-μ)/σ)x≥μ,

其中，σ>0为尺度参数，-∞<μ<∞为位置参数.

设X1,…,Xn是来自此总体的独立同分布样本，令

(1)

考虑双参数指数分布分位数的100(1-α)%广义置信区间,双参数指数分布的分位数μ-σln(1-α)，故构造广义枢轴量

(2)

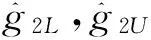
(3)

2 频率性质

主要研究了兴趣参数落在广义置信区间的覆盖概率，也就是广义置信区间的频率性质.

注：关于正规参数函数的定义参考文献[7].

证明

其中，FR1表示R1的分布函数.由于

(4)

证明过程与定理1类似，故略.

由定理1和2可知，由广义枢轴量确定的双参数指数分布的分位数及可靠度函数的广义置信区间的覆盖概率为1-α.

3 数值计算及实例

在数值模拟时，MonteCarlo方法提供了可行性保证.从而，计算双参数指数分布的兴趣参数的广义置信区间，可按步骤进行：

R(1)≤R(2)≤…≤R(m)；

步骤4 区间(R([mα/2]),R([m(1-α/2)]))可作为双参数指数分布兴趣参数的广义置信区间，其中[x]表示不超过x的最大整数.

例1[4]己知军队运兵车在服务中失效的行驶里程服从双参数指数分布f(x;μ,σ)，现随机抽取19辆军车的失效行驶里程记录为：

162，200，271，320，293，508，539，629，706，777，884，1 008，1 101，1 182，1 463，1 603，1 984，2 355，2 880，

分别计算在置信水平为0.9时，分位数和x0=706时可靠度函数的广义置信区间.

从模拟计算结果可知，当模拟次数m大于10 000时，兴趣参数的广义置信区间趋于稳定，对估计参数有较为满意的覆盖，精度也令人满意，更可取的是计算简单，计算速度快，是在应用中值得借鉴的方法.

[1]EpsteinB.Statisticalaspectsoffractureproblems[J].AppliedPhysics,1948,19(2):140-147.

[2]EasterlingRG.Exponentialresponseswithdoubleexponentialmeasurementerror:amodelforsteamgeneratorinspection:proceedingsoftheDOEstatisticalsymposium,Albuquerque,Nov1 1978[C].[S.l]:U.S.DepartmentofEnergy,1978.

[3]BainLJ,EngelhardtM.Intervalestimationforthetwo-parameterdoubleexponentialdistribution[J].Technometrics,1973,15(4):875-887.

[4]LawlessJF.StatisticalModelsandMethodsforLifetimeData[M].NewYork:JohnWiley,1982.

[5]EngelhardtM,BainLJ.Tolerancelimitsandconfidenceonreliabilityforthetwo-parameterexponentialdistribution[J].Technometrics,1978,20(1):37-39.

[6]WeerahandiS.Generalizedconfidenceintervals[J].JournaloftheAmericanStatisticalAssociation,1993,88(423):899-905.

[7] 徐兴忠，李国英.枢轴分布族中的Fiducial推断[J].中国科学A辑，2006，36(3):340-360.

[8]XuXZ,LiGY.Fiducialinferenceinthepivotalfamilyofdistribution[J].ScienceinChinaSeriesA:Mathematics,2006,49(3):410-432.

Generalized Confidence Intervals for Interest Parameters of the Two-Parameter Exponential Distribution

Yuan Shoucheng

(College of Mathematics and Statistical Science, Puer University, Puer 665000, China)

In the report, the generalized confidence intervals for the percentile and the reliability function of the two-parameter exponential distribution were investigated. Firstly, the concept of generalized pivotal quantity was used to propose the generalized confidence intervals of two interest parameters. Secondly, under the sense of frequency, their exact confidence levels were proved. At last, the numerical simulation experiment was performed, and the results confirmed the validity of the method.

two-parameter exponential distribution; generalized confidence interval; generalized pivotal quantity; Fiducial model

2016-10-20

普洱学院科学研究项目(201334)；微分方程研究与应用创新团队(K2015042)

袁守成(1981-)，男，甘肃景泰人，讲师，研究方向：应用统计学，E-mail：ysc-peace@163.com

1004-1729(2017)01-0022-04

O 211.3

A DOl：10.15886/j.cnki.hdxbzkb.2017.0005