基于正交试验方法的导弹保温舱盖运动控制参数优化

岳玉娜，王增全，吴 艳

（北京航天发射技术研究所，北京，100076）

基于正交试验方法的导弹保温舱盖运动控制参数优化

岳玉娜，王增全，吴 艳

（北京航天发射技术研究所，北京，100076）

根据总体指标对快速性和安全性的要求，制定评价导弹保温舱盖运动过程的指标，以优化该指标为目标，利用正交试验方法对某导弹保温舱盖的运动控制参数进行寻优匹配研究；通过分析正交试验结果，确定影响保温舱盖运动指标的主次因素，并得到标定控制参数的最优组合。结果表明，采用正交试验法能够以较少的代价实现参数的匹配优化。

正交试验；控制参数；优化

0 引 言

某型导弹的保温舱盖分为前后两部分，前后盖由4个开盖油缸在内的液压系统驱动，液压系统由控制系统控制，前后盖运动控制策略集成在控制流程中。在进行开盖运动过程控制系统设计过程中，首先通过机电液各系统主要性能参数进行初步匹配，确定一组控制参数。但由于控制系统参数众多，采用传统的试凑法难以把所有组合都考虑到，对控制参数进行整体优化的难度较大。

为了采用尽量少的试验次数得到比较全面的结果，利用保温舱开盖机电液联合仿真模型，根据总体指标对开盖过程的要求，制定评价舱盖运动过程的指标，利用正交试验设计方法对舱盖运动控制参数进行匹配寻优。通过分析试验结果，确定影响舱盖运动指标的主次因素，得到了优化后的运动控制参数。

1 机电液联合仿真模型

开盖过程机电液联合仿真模型如图1所示。开盖机械系统模型包括保温舱体、保温舱前后盖、驱动舱盖运动的4根油缸（执行机构），前盖2根油缸结构相同，后盖亦然。液压系统模型主要包括负载敏感泵、比例换向阀、螺纹插装式平衡阀及前后顶盖液压缸等模块[1]；控制系统模型主要包括控制流程及前后顶盖的开盖角度控制算法。

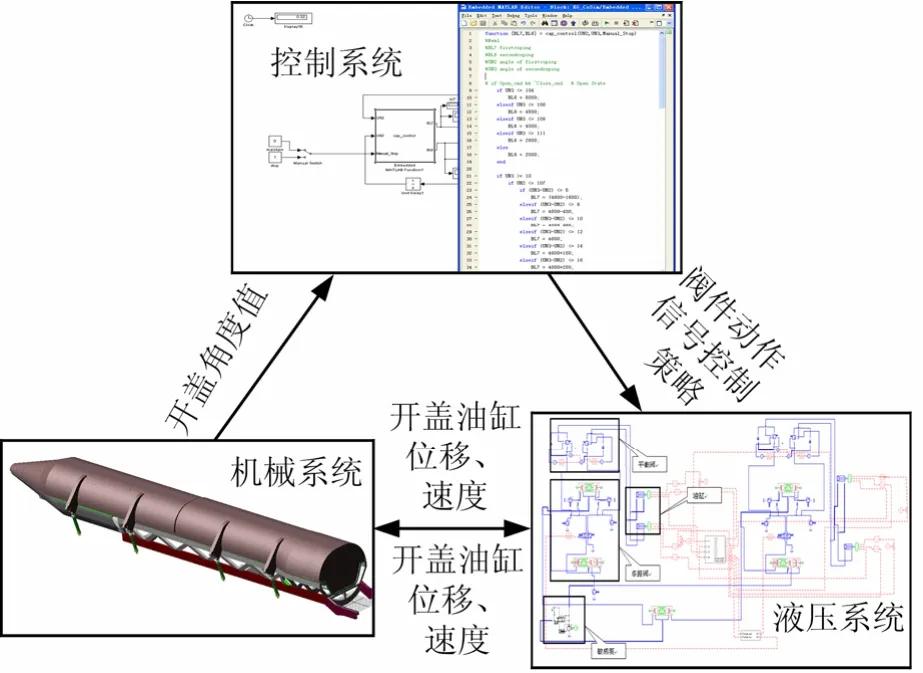
图1 开盖过程机电液联合仿真示意

2 正交试验法

正交试验设计法是利用数理统计学与正交性原理进行合理安排试验的一种科学方法[2]。在一项试验中，用来衡量试验效果的指标，称为试验指标[3]。要考虑的对试验指标可能有影响的变量称为因素，每个因素在试验中所处的状态称为该因素的水平。

正交表是正交试验法安排试验和分析试验结果的基本工具[4]，其必须具备的性质如下：

a）各水平在任何一列中都出现，且出现次数相等；

b）任意两列之间的各种不同水平的所有可能组合都出现，且出现次数相等。

在正交表中，任一列的各水平都出现，使得部分试验中包含所有因素的所有水平；任意两列的所有组合都出现，使得任意二因素间都是全面试验，这2个特点称为正交性。正交试验法对其中任意2个因素来说是具有等量重复的全面试验，这种特性称为整齐可比性[5]。这种均衡分散、整齐可比的特征，使得它具有代表性强、试验效率高等特点。

正交试验结果分析方法主要有极差分析法和方差分析法[6]。极差反映了所排因素的水平变动对试验指标影响的大小，极差值较大的因素是主要因素，极差值较小的因素是次要因素。极差分析法简便易懂，但不能估计试验过程中以及试验结果测定中必然存在的误差大小，为了弥补这个缺点，可采用方差分析法[7]。

选取因素的水平要与要求的指标相关，虽然把各因素的最好水平简单组合起来可以得到最优参数，然而实际选取时，还应考虑因素主次，对一些次要因素按节能、优质、低耗等原则进行选取，得到更为适合实际情况的较优参数组合[8]。

3 试验因素和水平确定

3.1 主要控制参数

保温舱开盖过程的控制流程如图2所示。其中UN2为前盖角度，UN3为后盖角度。开盖过程采取按开盖角度划分的分段控制策略，控制算法中包含6个主要控制参数，分别为BL8、△BL7、BL8a、BL7a、BL7b、BL7c，物理含义参见表1。

图2 开盖过程控制流程

表1 主要控制参数物理含义

续表1

3.2 评价指标

对于保温舱盖开启的运动过程，由于总体指标对发射流程时间的限制，必须关注其快速性。在角度行程一定的条件下，快速性取决于盖体运动角速度，角速度越大，开盖时间越短。同时，保温舱盖的结构和质量分布决定了在运动过程中，作为执行机构的开盖液压缸的受载不同以及盖体受力不均，可能造成舱盖结构破坏，因此还必须要关注开盖运动的安全性。安全性主要取决于每组液压缸之间的载荷差，载荷差越小，受力越平均，盖体运动过程越安全。因此，要制定开盖运动的性能评价指标就应该对整个过程进行全面考虑，为此，选取如式（1）所示的开盖运动评价指标。由该指标的定义可知，指标值越小，证明开盖过程既快速又稳定安全。

式中 T1为前盖开盖完成时间；T2为后盖开盖完成时间；T3为前盖两油缸载荷差绝对值大于某设定阈值的总时间，该阈值取所有试验前盖油缸载荷差绝对值最大值序列的均值； T4为后盖两油缸载荷差绝对值大于某设定阈值的总时间，该阈值取所有试验后盖油缸载荷差绝对值最大值序列的均值；ω1为前盖开盖角速度；ω2为后盖开盖角速度；F1Δ为前盖油缸载荷差；ΔF2为后盖油缸载荷差；为前盖油缸载荷差绝对值最大值；为后盖油缸载荷差绝对值最大值；为超过的部分；为超过的部分；α1，α2，α3，α4为权重系数，α1+α2+α3+α4=1，本文取α1=α2=α3=α4=0.25。

3.3 试验因素和水平

本文将开盖过程的6个主要控制参数作为试验因素，分别取各个因素的2个水平，确定正交试验的因素和水平，如表2所示。

表2 试验因素和水平

4 试验分析

由开盖运动流程及各参数含义可知，后盖的运动状态对开盖过程具有至关重要的作用，因此，初步认定后盖运动控制量的主要控制参数 8BL（试验因素 A）的作用十分关键。为了重点探索因素A对试验结果的影响，本文考虑6个试验因素的单独作用，以及因素A与其他5个试验因素的交互作用，不考虑其他交互作用，选取正交表L16（215）。

4.1 极差分析

极差分析正交试验结果计算如表3所示，仿真计算结果从略。

由表3中极差的大小顺序可以得出各因素水平不同对评价指标值的影响大小[9]，可以确定因素A和A与B的交互作用是影响指标的重要因素，其他因素为次要因素。

表3 极差分析正交试验结果计算

4.2 方差分析

为了更进一步地确定重要影响因素对试验误差进行估计，以及探索参数的优化方向，还需要对开盖控制过程的正交试验进行方差分析。为了估计试验误差的大小，需要在正交表中留出空白列。获取方差分析的试验计算结果如表4所示。

表4 方差分析正交试验结果计算

表4中的列号第6、7、14和15没有赋予内容，它们的平方和反映了试验误差，因此试验误差的平方和可以通过没有安排因素的列直接计算，给出了直接计算的内容。其中，自由度的计算规则如下：

利用因素均方与误差均方的比值可以检验因素影响的显著性，对本试验中的因素进行F检验的结果如表5所示。由于在正交试验中误差的自由度f误通常比较小，由数理统计理论可知，F检验只有当f误较大时检验的灵敏度才较高。因此，如果 f误≤5，计算出 F值介于表上F0.1与F0.2之间的，则此因素对指标有一定影响，标记为“△”。

因D、E、F、A×C、A×D、A×F列的平方和较小，可将它们合并到试验误差中去，即平方和的合并、自由度的合并，计算误差均方如下：

将合并后的试验误差均方用于F检验，结果表明，A、A×B对试验影响最大，B次之，C有一定影响。A与B之间有显著的交互作用存在，可通过二元表（表6）或二元图（图 3）以确定最优搭配水平，取 A2B1为最优。

表5 方差分析

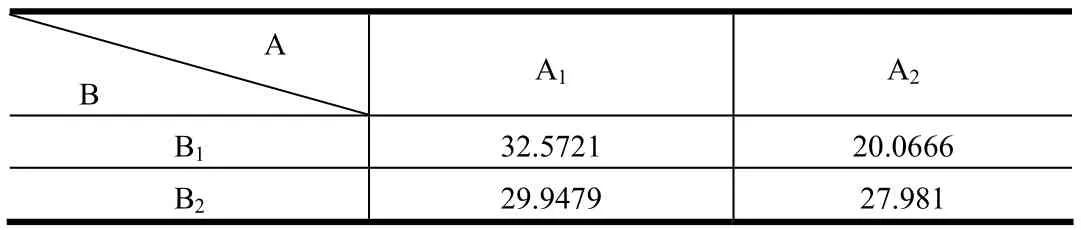
表6 二元水平体系A、B二元交互作用

图3 二元水平体系A、B二元交互作用

5 参数优化

通过上述试验分析可以看出，极差分析和方差分析得出了一致的结论，而且方差分析还能对误差的影响给出定量估计结果。

若令指标达到最好水平，则选择因素组合A2B1，对应于9、10、11、12号试验。对于次要因素，虽然10号试验组合 C1D2E1F1使指标值达到最小，前盖开启用时21.87 s，后盖开启用时15.03 s。但实际仿真结果显示，前盖油缸载荷差峰值为1 575 N，后盖油缸载荷差峰值为9 780 N，安全性较差。综合考虑，选取使指标值次小的因素组合A2B1C1D1E2F2（9号试验），在此条件下前盖开启用时22.2 s，后盖开启用时15.03 s，前盖油缸载荷差峰值为1 469 N，后盖油缸载荷差峰值为2 645 N。

进行正交试验参数优化探索前后的控制参数对比如表7所示。分别取两组参数进行开盖过程仿真，仿真结果及评价指标对比如表8所示。仿真曲线对比如图4所示。从上述对比可以看出，经过参数优化后，开盖过程运动指标得到了较好的改进。

表7 优化前后参数对比

表8 优化前后仿真结果及评价指标对比

图4 优化前后仿真曲线对比

6 结束语

本文针对某导弹保温舱盖运动过程，利用机电液联合仿真模型，通过正交试验法进行了控制参数灵敏度分析及优化，得出了对舱盖运动控制具有显著影响的控制参数，实现多种参数组合情况下通过较少的仿真试验进行控制参数的优化匹配，为控制系统参数优化与仿真试验提供了高效的分析方法，该方法还可以推广应用与机械、液压等单学科和多学科设计优化中。

[1]王增全, 等. 基于机电液一体化仿真技术的发射车开盖过程设计与优化[J]. 导弹与航天运载技术, 2016(6):1-5.

[2]何为, 等. 优化试验设计方法及数据分析[M]. 北京: 化学工业出版社, 2014.

[3]李玉璇, 等. 利用正交试验法进行 ABS控制参数的优化[J]. 机械科学与技术, 2002(21): 58-60.

[4]盛永莉. 正交试验设计及其应用[J]. 济南大学学报(综合版), 1997(3): 69-73.

[5]曾小华, 王庆年, 王伟华, 初亮. 正交优化设计理论在混合动力汽车设计中的应用[J]. 农业机械学报, 2006(5): 26-28.

[6]刘瑞江, 张业旺, 闻崇炜, 汤建. 正交试验设计和分析方法研究[J]. 实验技术与管理, 2010(9): 52-55.

[7]王岩, 隋思涟. 试验设计与MATLAB数据分析[M]. 北京: 清华大学出版社, 2012.

[8]刘振明, 等. 高压共轨柴油机怠速工况喷射控制参数匹配研究[J]. 小型内燃机与摩托车, 2011, 40(3): 1-4.

[9]胡坤, 刘滨涛. 基于参数灵敏度分析的航天器毁伤效能研究[J]. 计算机仿真, 2011(10): 52-56.

Control Parameters Optimization of Missile Heat Container Motion Based on Orthogonal Experiment Method

Yue Yu-na, Wang Zeng-quan, Wu Yan
(Beijing Institute of Space Launch Technology, Beijing, 100076)

An evaluation index for missile heat container motion is established according to the requirements for rapidity and safety. Orthogonal experiment design method is adopted for parameters match and index optimization. Primary influential factors, as well as optimum combination of control parameters are achieved through results analysis of orthogonal experiments. The results indicate that parameters optimization can be realized with less cost using the method proposed in this paper.

Orthogonal experiment; Control parameters; Optimization

V553.2

A

1004-7182(2017)01-0070-06

10.7654/j.issn.1004-7182.20170117

2016-05-06；

2016-09-04

岳玉娜（1984-），女，工程师，研究方向为复杂系统仿真与虚拟试验