新型振荡发生装置的研究

顾 尧，孔 委，陈剑雄，郑辉东

(1.福州大学石油化工学院，福建 福州 350116；2.福州大学机械工程与自动化学院，福建 福州 350116)

新型振荡发生装置的研究

顾 尧1，孔 委1，陈剑雄2，郑辉东1

(1.福州大学石油化工学院，福建 福州 350116；2.福州大学机械工程与自动化学院，福建 福州 350116)

设计并制作一种提供正弦位移振荡且频率可调、振幅无级可调的新型振荡发生装置，阐述其结构设计及原理.运用数学分析方法计算振荡发生装置振幅位移随时间的变化，发现振幅随时间的变化并非严格的正弦，其上半周期与标准正弦图形重合度较好，下半周期位移与标准正弦有偏差.同时，采用实验方法验证振荡发生装置在运行过程中实际振幅随时间的变化，发现与理论计算值有一定偏差，但仍呈正弦位移运动趋势，且振幅值精度较高.

管式振荡流混合器；振荡发生装置; 运动分析; 正弦位移

0 引言

近年来，管式振荡流混合器作为一种新型高效的化学反应设备与过程强化装置受到了广泛关注，关于其传质传热性能[1-3]、新型内构件[4-5]等都有学者进行了深入的研究.管式振荡流混合器中的振荡发生装置是实现振荡流的关键核心设备之一，对振荡条件控制起关键性作用，但其相关研究却较少.目前，实现振荡流的装置大多采用现有的往复泵来替代，对振荡幅度和振荡频率的控制精度较低.

目前，已有的实现振荡流装置大致分以下几种：

1)隔膜泵改装[6].将隔膜泵的入口切断，出口单向阀拆除，或将隔膜泵出口与入口相连通，反应器均能接收稳定的周期振荡.隔膜泵电机为变频电机即可实现频率调节，隔膜泵活塞杆与偏心轮之间形成的间距控制机构可实现振幅调节.但由于改装进出口，而且振幅调节常以调节行程来标识，往往能判断调节幅度而不清楚具体振幅数值，使用时需用体积的转换关系以及振荡流反应器管尺寸来标定振幅.

2)曲轴泵.邓勇等[7]的漂浮实验装置中其振荡发生装置与隔膜泵类似，差别主要在密封方式，相当于上文提到的切断入口，出口去除单向阀.但该实验装置没有膜片，振幅控制不精确.

3)偏心泵[8-9].偏心泵利用凸轮与传动杆偏心而产生周期变化，当电机带动传动杆转动时，凸轮转动而产生周期位移.凸轮离轴偏心度不同则振幅也不同，则通过改变凸轮与活塞杆接触位置可以改变振幅.振幅可以通过测量凸轮与杆心的偏离距离得到.而频率则通过改变电机转速调节.但该装置振幅调节比较麻烦，且振幅控制精确度不高.

可以发现，现有振荡发生装置多为频率(转速)可调而振幅(冲程)固定或难调的传动机构，且控制精度差，这一定程度上限制了研究及应用的发展.因此，本研究设计了频率和振幅在一定量程内连续可调且精确度高的振荡发生装置.

1 振荡发生装置的设计及原理

采用行程无级可调的往复式柱塞泵作为振荡发生装置，三维结构设计如图1所示.振荡发生装置平面图如图2所示.其中，壳体前端内嵌有柱塞缸套，柱塞缸套内设置有沿其轴向往复运动的柱塞，柱塞后端通过球头连杆与转盘偏心铰接，转盘旋转时通过球头连杆带动柱塞旋转，转盘嵌设于摆动座内.摆动座、转盘、球头连杆及柱塞组成空间曲柄滑块机构，摆动座摆动时带动转盘同步摆动以改变转盘的旋转平面与柱塞轴线的夹角，进而无级调节柱塞行程，使振幅发生改变[10].频率改变则通过调节电机转速来实现.

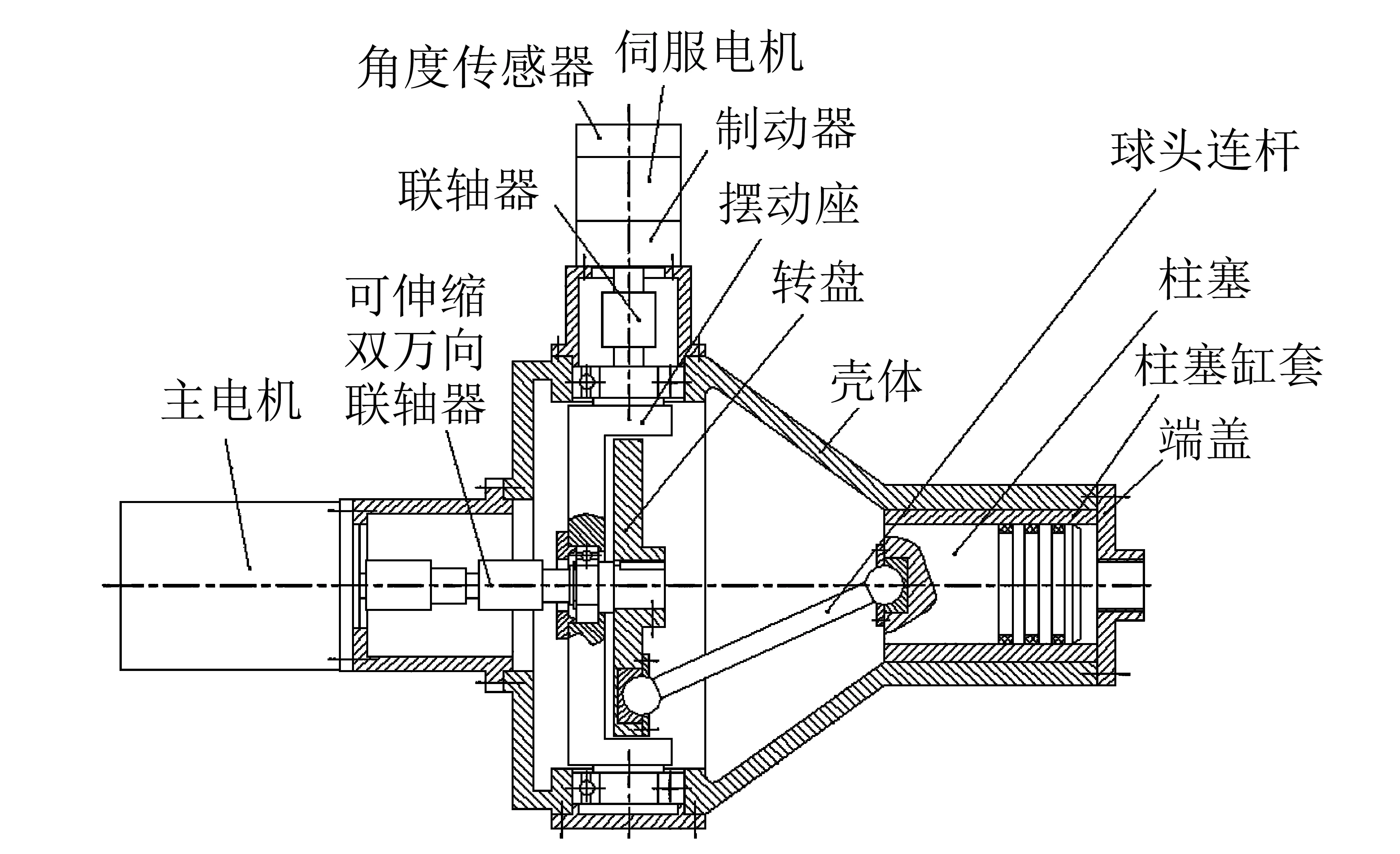
图2 振荡发生装置平面图Fig.2 2D stereogram of the oscillation generator

由于转动过程中转盘活塞位移变化非线性，转动时所需扭矩不同，电机输出负荷变化而影响转速值，本实验装置通过减速器增大转矩来减小旋转扭矩对转速的影响.振幅在柱塞、转盘大小尺寸和杆长固定时，振幅范围确定.因此，机械设计需根据操作振幅范围来确定转盘尺寸和杆长.振幅只通过调节转盘偏离角度来实现，由于角度偏离越大，扭矩在转动的整个周期中越不均匀，稳定性越差，因此实际应用中只取偏离角度<15°.由于活塞筒与杆之间是通过螺栓连接，因此,可通过更换不同直径柱塞筒来改变其容积，即可改变振幅.

综上所述，本设计实现了往复式柱塞泵柱塞运动行程的无级可调，采用伺服电机(北京时代超群电器科技有限公司，57BL90-230)提高了振幅和频率的调节精度，达到了振荡装置所需提供的条件及要求.

2 振荡发生装置的运动分析

振荡发生装置振幅的计算以及柱塞速度对实际应用十分重要，借助数学分析得到理论公式，并采用高速摄像机进行实验验证.频率的调节通过控制电机转速实现，已采用转速测量仪对装置运行频率进行验证，具备较高的精确度.

2.1 数学分析

振荡发生装置转盘简化为如图3所示的平面1，转盘初始位置位于XZ平面内，转盘上位于X轴正方向A点，在转盘转动时间t之后，到达平面2，坐标如图4所示.假设转盘角速度为ω，则时间t后，转盘上A点转过角度为α=ωt.所以，A点在XZ平面内坐标为(Rcosα，Rsinα)，三维坐标为(Rcosα，0，Rsinα).

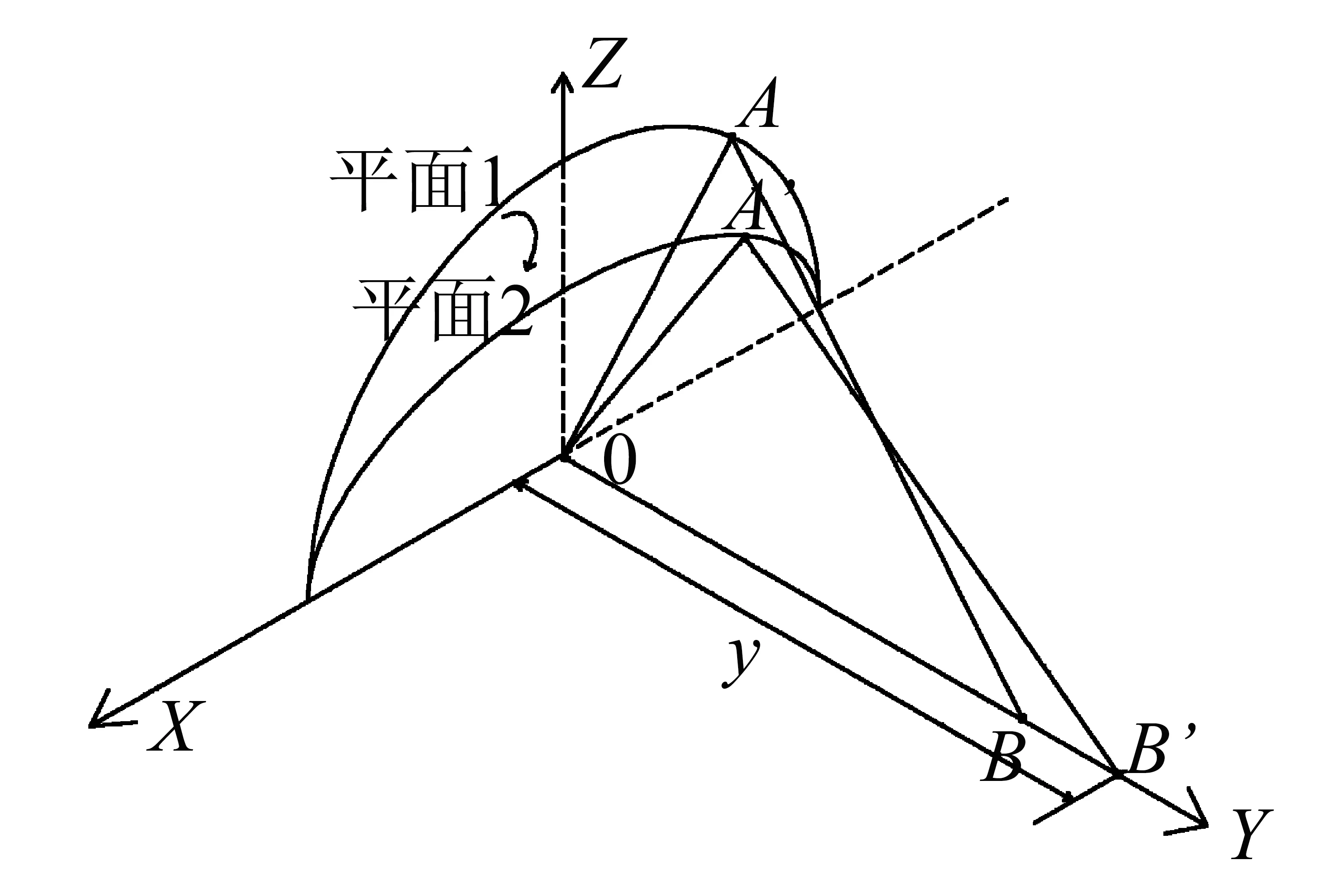
图3 振荡泵几何简化原理图Fig.3 Simplified graphic of the oscillation generator

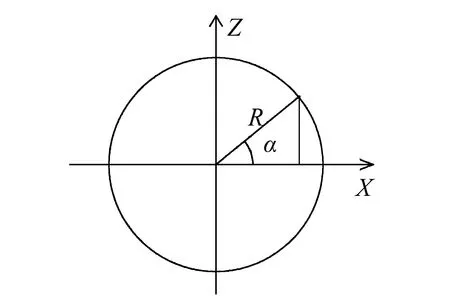
图4 转盘转角示意图Fig.4 Diagram of the rotary angle

当平面1绕着X轴顺时针旋转θ之后，根据旋转变换原则依照θ角正方向旋转(即满足右手螺旋法则)，有：

平面1经过旋转之后，位于平面2，转盘上A点位置转换为A′，则有：

即A′(Rcosα，Rsinα·sinθ，Rsinα·cosθ).

在柱塞泵的工作过程中，球头连杆AB长度L为定值，当A点发生改变，对应连杆AB端点B的坐标也会发生改变.通过简化，活塞的运动轨迹可以近似看成为B点在时间t内位移(y坐标).至平面2后，B点位于B′点，则B′的坐标为(0,y,0).球头连杆为A′B′长度不变.根据空间两点距离公式，得：

其中:α=ωt，将公式(3)化简解得B点的运动方程，为：

B点运动速度的计算，即上式对时间t求导：

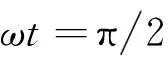
可得偏离角度与振幅的关系：

由振幅变化的单调特性，可知在ωt=0有极值，由区间有界性和极值个数可判知该极值点为最值点，设在ωt=0时,最大速度为vmax，将公式(7)代入公式(5)中，有：

由公式(6)可以看出，振幅随时间的变化并非严格的正弦，可将测得的振幅和已知频率代入振幅公式，用Matlab作图，并与标准正弦曲线进行对比，如图5所示.

由图5可以看出，在上半周期时振幅与标准正弦图形重合度较好，而下半周期位移与标准正弦有偏差，表现为不对称周期振荡，对于不对称性的强弱用不对称因子k0表示.邓勇等[7]定义k0为向上的平均速度与向下的平均速度之比.柱塞泵速度随时间变化如图6所示，表现出的对称性较好，可表明不对称因子k0较小.

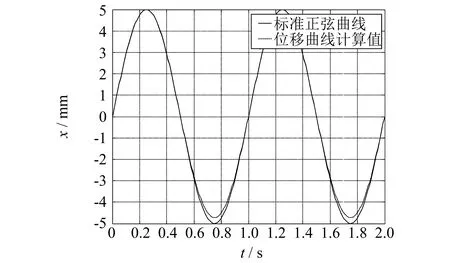
图5 振幅x随时间t关系(振幅5 mm，频率1 Hz)Fig.5 Amplitude versus time(amplitude=5 mm,frequency=1 Hz)

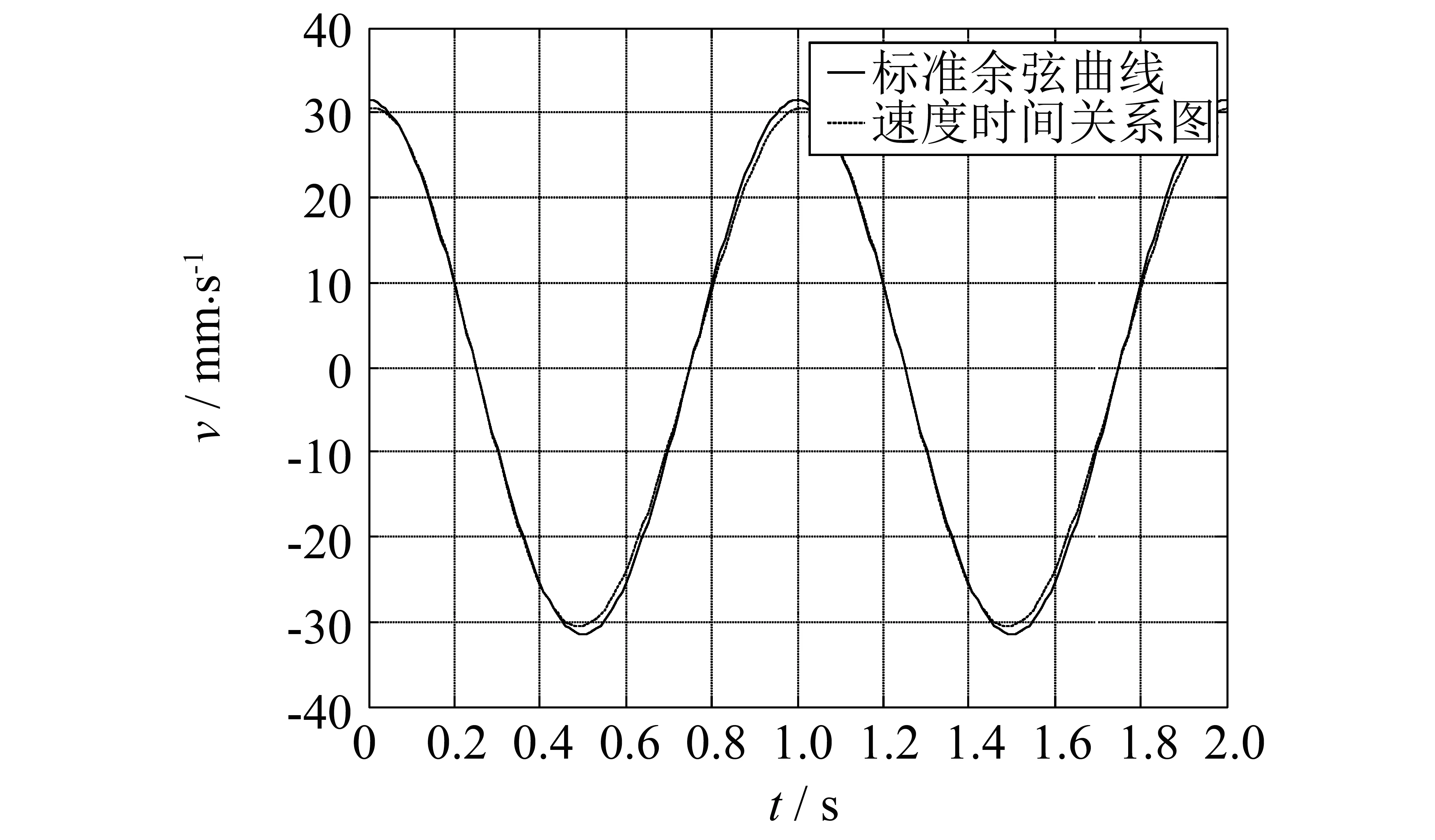
图6 活塞速度v随时间t关系(振幅5 mm，频率1 Hz)Fig.6 Piston speed versus time (amplitude=5 mm,frequency=1 Hz)

从图6中可以看出，与位移对称性相比，速度随时间的变化与标准余弦函数也有偏差，但相对偏差明显小于位移图像，并表现出良好的对称性，这是因为速度小于零的区间在空间上是转盘最高点到转盘最低点，而速度大于零是转盘最低点到转盘最高点空间位置的对称性决定的.

图7与图8为绝对速度偏差Δ与相对速度偏差δ.可以看出，在最大速度为30 mm·s-1时，绝对速度偏差小于1.5 mm·s-1，相对速度偏差控制在8%以内.这在毫米级别上看误差较小，呈现出较高的精确度.

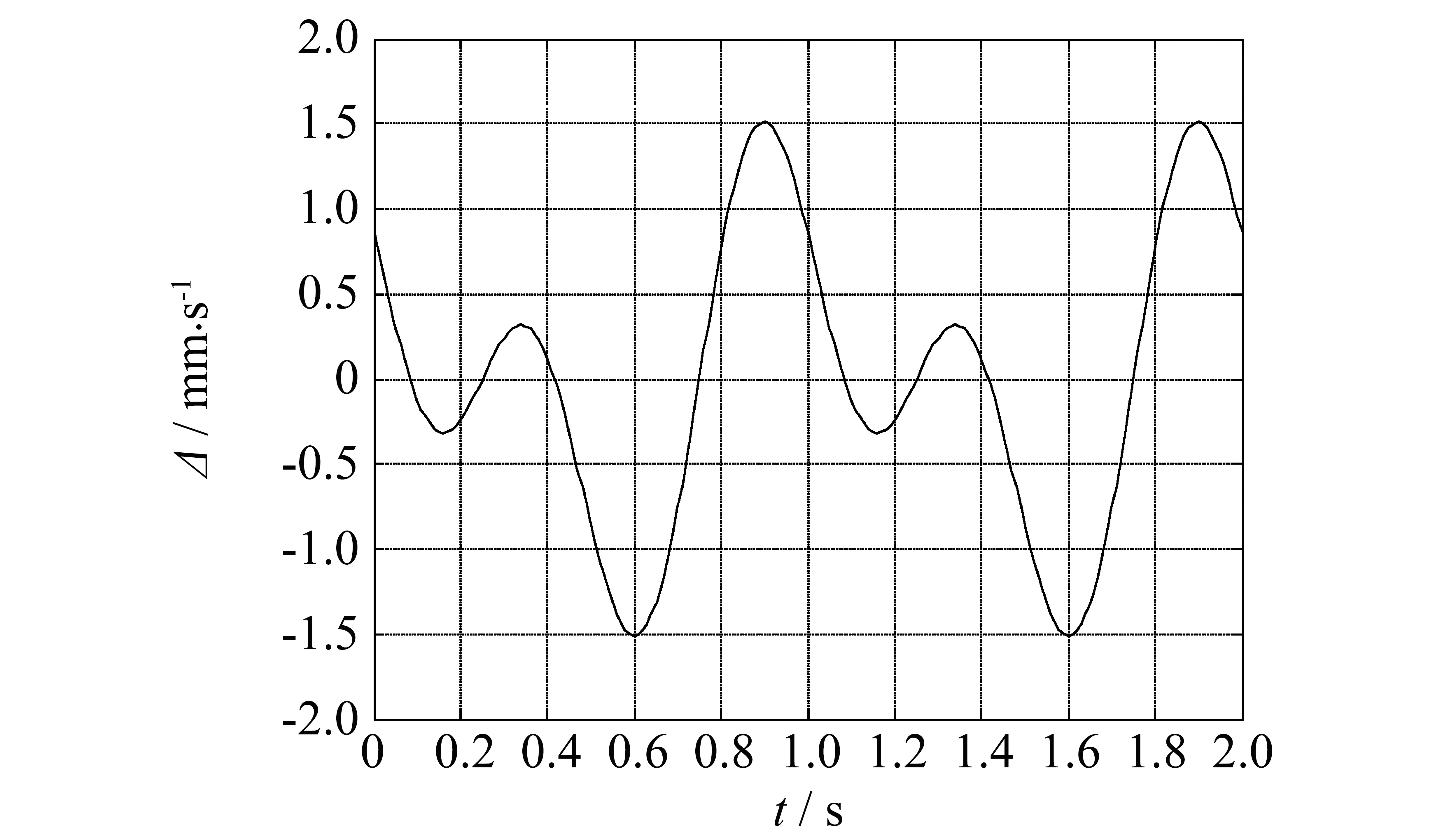
图7 绝对速度偏差Δ随时间t关系(振幅5 mm，频率1 Hz)Fig.7 Absolute speed deviation versus time (amplitude=5 mm,frequency=1 Hz)

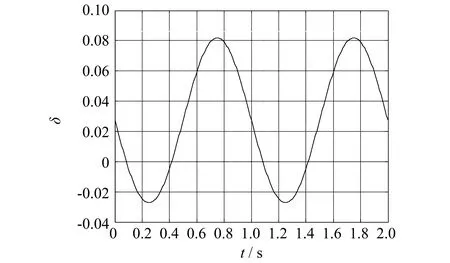
图8 相对速度偏差δ随时间t关系(振幅5 mm，频率1 Hz)Fig.8 Relative speed deviation versus time (amplitude=5 mm,frequency=1 Hz)

2.2 实验验证

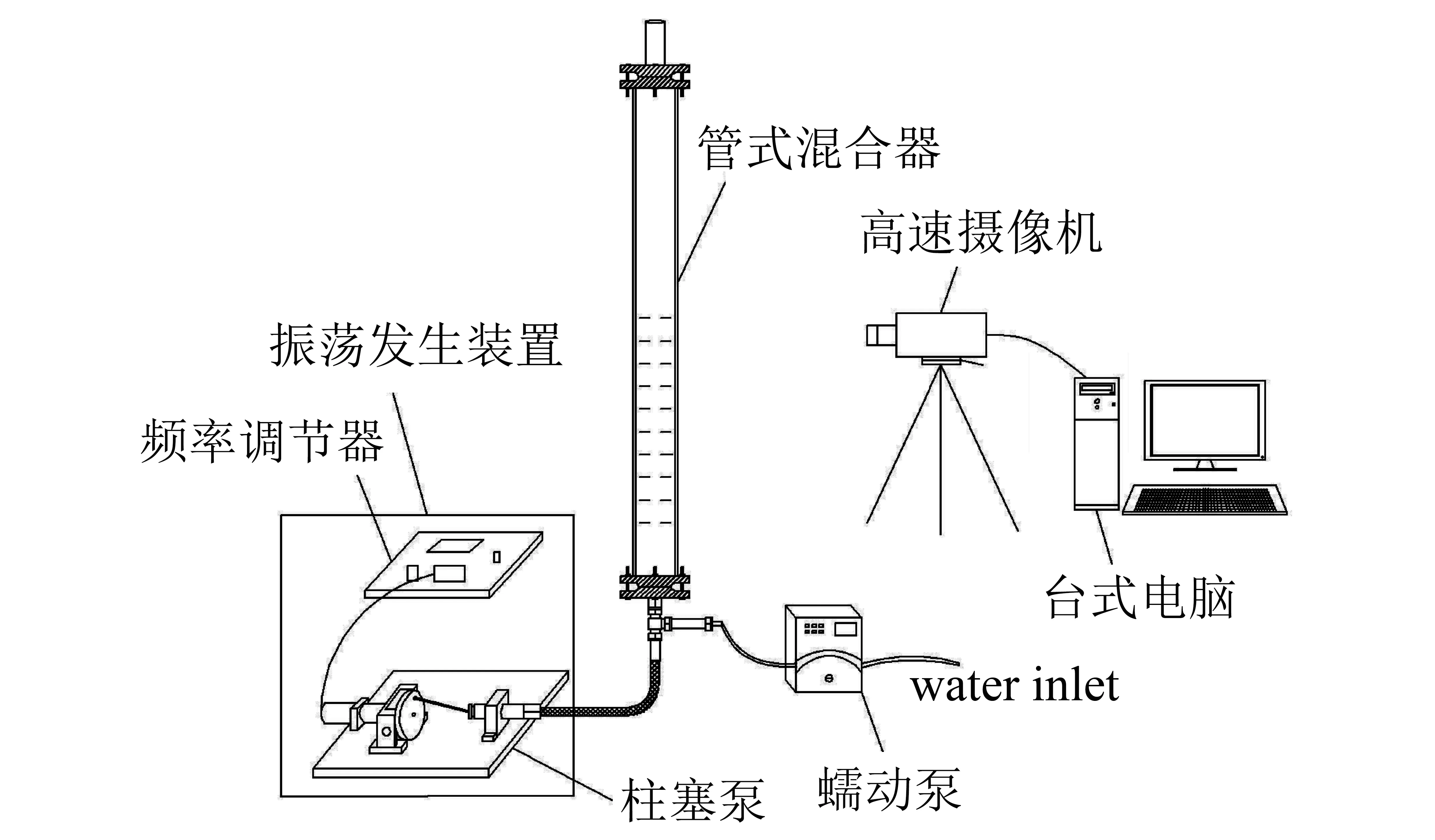
图9 振幅验证实验装置图Fig.9 Experimental setup for amplitude verification

前述数学模型是建立在理想状态下的理论分析结果.然而,在振荡发生装置实际运行过程中，由于机械阻力的影响，真实的振幅变化可能会与计算值有所误差.为了验证柱塞泵使用时的实际效果，采用高速摄像机[11]来测量流体振幅随时间的变化，实验装置如图9所示.验证实验所采用的管式振荡流混合器由振荡发生装置和管式混合器组成，管式混合器外附有标尺(见图10).实验时，水通过蠕动泵加入混合器直到一定的液位，调节振荡发生装置的振幅和频率，开启实验装置，使其发生振荡.用高速摄像机采集图像，每秒采集500张，采集的图像如图10所示.采集2 s共1 000张图片，再从中均匀抽取50张图片读取实际位移，得到振幅随时间的变化规律，如图11所示.

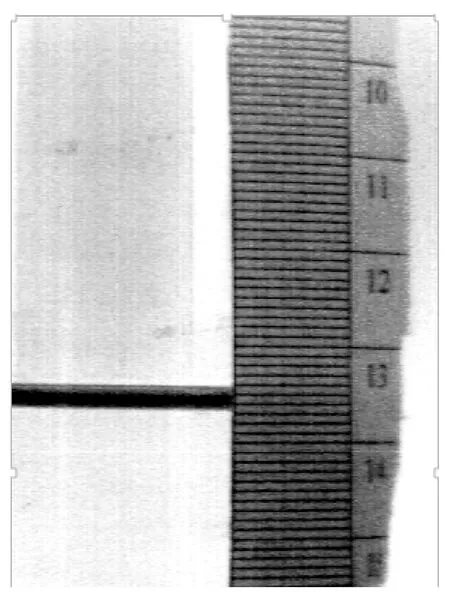
图10 高速摄像机拍摄的振荡流反应器标尺图Fig.10 Rulers on oscillatory flow reactor captured by a high-speed camera

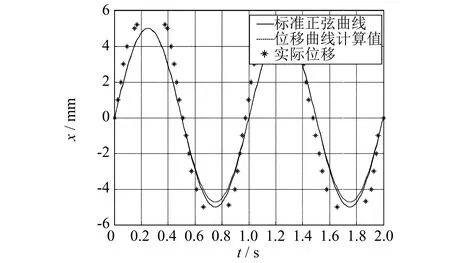
图11 振幅x随时间t关系(振幅5 mm，频率1 Hz)Fig.11 Amplitude versus time (amplitude=5 mm,frequency=1 Hz)

由实验结果可知，实际振幅与标准正弦曲线及柱塞泵位移曲线(见式(6))计算值存在一定误差.这是由于在振荡装置实际运行中存在一定的机械阻力，导致活塞在振幅最高点和最低点处的运行有所滞缓.总体来说，实际的振荡泵位移变化仍然呈正弦趋势，装置对振幅与频率控制较精准，可以满足实际应用的要求.

3 结语

本研究设计了以柱塞泵为原型的新型振荡发生装置，由摆动座、转盘、球头连杆及柱塞组成空间曲柄滑块机构.摆动座带动转盘改变其旋转平面与柱塞轴线的夹角，无级调节柱塞行程而改变振幅，并通过电机转速来控制频率.本研究对振荡发生装置的振幅进行了计算分析及实验验证.分析结果表明，该振荡发生装置提供的振荡曲线近似正弦曲线，速度随时间变化近似标准余弦曲线.实验结果表明，因机械阻力的影响，该装置在实际运行过程中呈现的位移变化与标准正弦曲线及理论分析都有所偏差，但对振幅与频率的控制精度很高.

[1] MCDONOUGH J R,PHAN A N,HARVEYA P.Rapid process development using oscillatory baffled mesoreactors：a state-of-the-art review[J].Chemical Engineering Journal,2015,265:110-121.

[2] AL-ABDULY A,CHRISTENSEN P,HARVEY A,etal.Characterization and optimization of an oscillatory baffled reactor (OBR)for ozone-water mass transfer[J].Chemical Engineering and Processing:Process Intensification,2014,84：82-84.

[3] SOLANO J P,HERRERO R,ESPíN S,etal.Numerical study of the flow pattern and heat transfer enhancement in oscillatory baffled reactors with helical coil inserts[J].Chemical Engineering Research and Design,2012,90(6):732-742.

[4] MACKLEY M R,NI X.Experimental fluid dispersion measurements in periodic baffled tube arrays[J].Chemical Engineering Science,1993,48(18):3 293-3 305.

[5] PHAN A N,HARVEY A.Development and evaluation of novel designs of continuous mesoscale oscillatory baffled reactors[J].Chemical Engineering Journal,2010,159(1/2/3):212-219.

[6] KONING D，JOHANNES C.Diaphragm pump:PCT/NL03/00497[P].2004-01-22.

[7] DENG Y,KWAUK M.Levitation of discrete particles in oscillating liquids[J].Chemical Engineering Science,1990,45(2):483-490.

[8] STONESTREET P,VAN DER VEEKEN P M J.The effects of oscillatory flow and bulk flow components on residence time distribution in baffled tube reactors[J].Chemical Engineering Research and Design,1999,77(8):671-684.

[9] HERRINGE R A.On the motion of small spheres in oscillating liquids[J].The Chemical Engineering Journal,1976,11(2):89-99.

[10] 陈剑雄,彭育辉,蓝兆辉,等.一种行程无级可调的往复式柱塞泵:204493161[P].2015-07-22.

[11] COURTNEY-PRATT J S.Simple high speed framing cameras[J].Journal of Scientific Instruments,1961,38(6):264-265.

(责任编辑：沈芸)

Study on a novel oscillation generator

GU Yao1,KONG Wei1,CHEN Jianxiong2,ZHENG Huidong1

(1.College of Chemical Engineering，Fuzhou University，Fuzhou，Fujian 350116，China;2.College of Mechanical Engineering and Automation，Fuzhou University，Fuzhou，Fujian 350116，China)

A novel type of oscillation generator was designed to create the sine displacement with continuously controllable frequency and amplitude.The structure and the principles of the device were described in detail.A theoretical mathematical model based on the geometric analysis was built to describe the variation of the amplitude over time.The analysis result shows that the variation of amplitude with time was not in strict accordance with a standard sinusoidal curve.Good agreement with the sine curve was observed at the first half period while a slightly deviation was found at the second half.Experimental measurements were carried out to validate the model and we found that there was a small deviation between the mathematical model and the actual movement.Overall,the new oscillation generator could provide the desired sinusoidal motion with precise amplitude.

tubular oscillatory flow mixer; oscillation generator；motion analysis; sine displacement

10.7631/issn.1000-2243.2017.02.0275

1000-2243(2017)02-0275-05

2015-10-12

郑辉东(1979-)，副教授，博导，主要从事化工过程强化研究，youngman@fzu.edu.cn

国家自然科学基金资助项目(21476049)；福建省科技厅工业高校产学合作基金资助项目(2014H6002)；福建省科技厅工业高校产学区域发展基金资助项目(2016H4023)

TQ016.5

A