高速公路可变限速优化控制模型

吴德华，林 毅

(福州大学土木工程学院，福建 福州 350116)

高速公路可变限速优化控制模型

吴德华，林 毅

(福州大学土木工程学院，福建 福州 350116)

针对METANET基本模型在预测交通拥堵路段时误差较大的缺陷，对车速和流量模型进行修正.提出高速公路可变限速修正模型并确定了可变限速阈值和变化频率；应用仿真对模型进行校准、验证和应用效果分析.仿真结果显示，修正模型的应用可降低交通总运行时间28.6%～33.2%，提高通过总车公里数1.8%～3.0%，提高通过总交通量2.00%～3.27%，证明了修正模型的适应性和有效性.可变限速变化阈值取10 km·h-1及变化频率取5 min时的组合效果最佳，可降低交通事故率50%.

高速公路；可变限速模型；仿真；限速阈值；限速变化频率

0 引言

随着交通需求的不断增加，交通拥堵和安全问题已受到广泛关注.为了缓解高速公路的交通拥堵、提高交通安全水平，动态交通管理和控制逐步得到应用和推广.常用的动态交通控制方法有动态可变限速、匝道控制、路线诱导等，文献[1-4]在仿真试验中得到动态可变限速策略可以不同程度降低交通事故率，提高拥堵路段通行能力.动态可变限速策略的有效性在美国、欧洲、澳大利亚等国家的工程实际应用中陆续得到验证，如美国密苏里州圣路易斯I-270和I-255公路应用后总的事故率降低了11%；英国M25公路交通事故率降低了30%，M42公路通行能力平均增加了7%～9%；德国的Autobahns公路交通事故率降低了20%～30%，A3公路通行能力平均增加了3%；澳大利亚M4和F3公路交通事故率降低了11%～24%[5].国内对高速公路可变限速控制策略也有一些研究成果，文献[6-8]分别对高速公路主线瓶颈路段及收费站建立相关模型进行仿真，得到相应研究成果.然而，动态可变限速预测中的核心问题，即可变限速预测模型的适应性与可变限速阈值及变化频率采用尚无统一意见，本研究在METANET基本模型[9]的基础上，针对METANET模型在预测拥堵路段时误差较大的缺陷，提出修正模型，并在仿真中对模型进行验证，确定可变限速的变化量阈值和变化频率，为动态可变限速的推广和应用提供参考.

1 可变限速控制策略核心模块

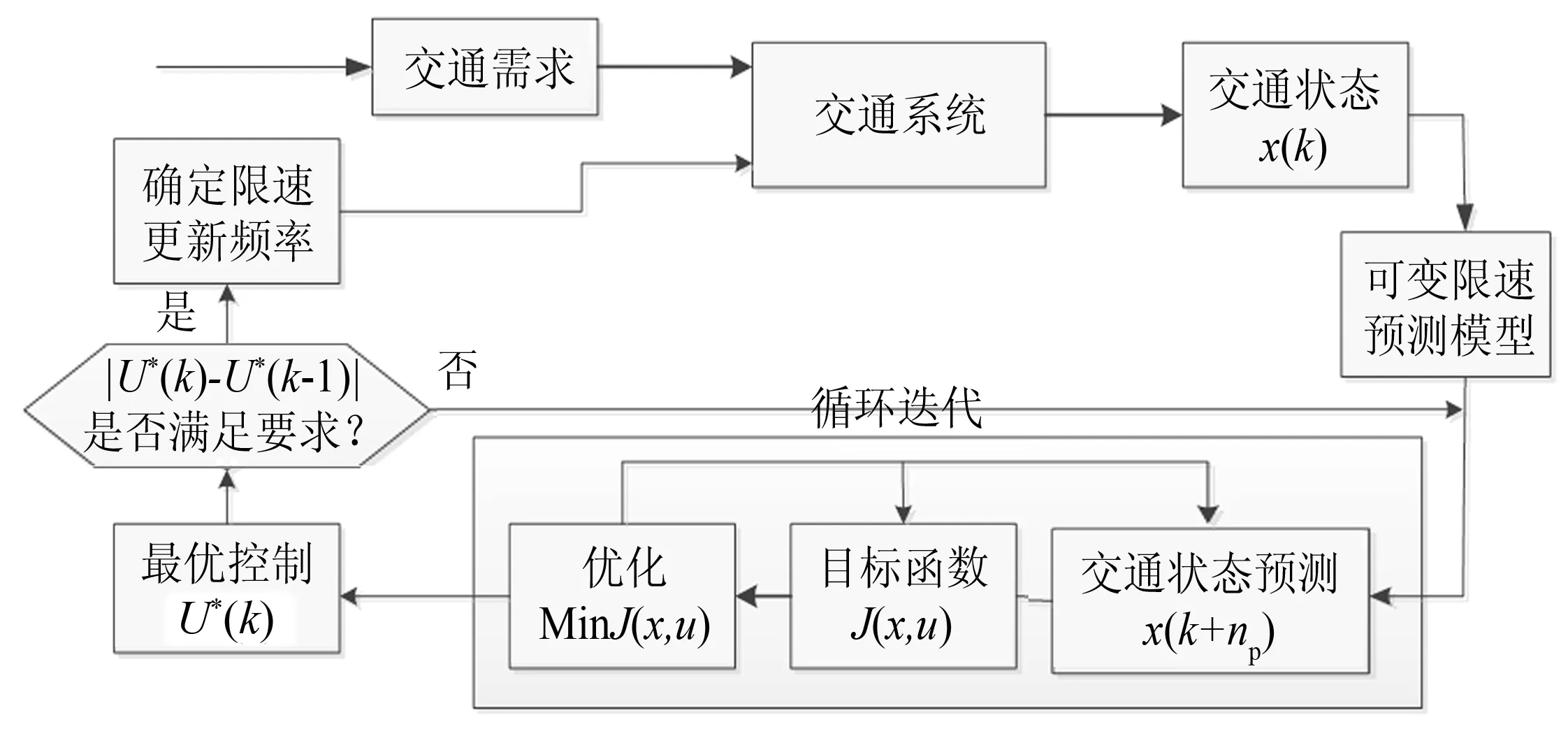
图1 可变限速控制策略流程图Fig.1 Structure diagram of varied speed limits control

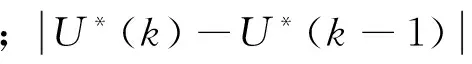
2 可变限速预测模型

2.1 基于METANET的可变限速修正模型

将高速公路划分成M段(见图2)，k代表时间刻度，T代表预测的时间步长；ρi(k)、vi(k)、qi(k)分别代表第k时刻、第i个路段上交通密度、平均车速和交通量；ri(k)、si(k)分别为第k时刻、第i个路段进口匝道和出口匝道的流量；λi为第i个路段的车道数；Li为第i个路段的长度(满足Li≥vfree·T)；vfree,i为第i个路段的自由流车速；ρc,j为第i个路段的临界密度；ρjam,i+1为第i+1个路段的拥堵密度；wi+1为第i+1 个路段交通波波速；τ、υ、kkappa为模型参数，则METANET基本模型如下列式子所示[8].

图2 高速公路路段图Fig.2 Section of freeway diagram

在METANET模型中，通行能力的预测由流量与密度的基本关系图进行换算，没有考虑在不同限速条件下拥堵路段通行能力的突降现象(capacitydrop)[10].在可变限速情况下，METANET模型在应用中的主要缺陷如下：1)一般流量密度基本图关系在平衡交通条件下才成立，而高速公路拥堵路段受道路几何条件和驾驶行为影响，交通流通常是不平衡的；2)高速公路受突增交通量或不可预测意外事故影响而发生拥堵时，会发生通行能力突变，突变量的大小在已有的模型中无法体现，导致预测结果误差较大.

为了克服METANET模型预测交通拥堵路段时存在的缺陷，分别对车速和密度模型进行修正：

1)车速模型的修正.用可变限速控制车速替代由非线性的流量密度基本关系推算得到的车速，即用ui(k)替代Ve,i(ρi(k))，修正后式(1)变成式(5)，修正后的可变限速车速模型更加简洁和准确.

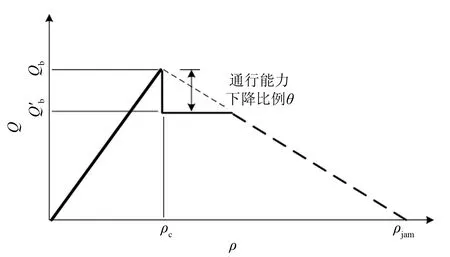
图3 拥堵路段交通流量下降基本图Fig.3 Fundamental diagram of capacity drop on bottleneck segment

2)流量模型修正.考虑不同限速条件下拥堵路段通行能力突变问题(见图3)，增加对拥堵路段通行能力突变值预测，修正后拥堵路段流量模型由式(3)演化为式(6)：

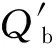
2.2 修正模型的约束条件

考虑到高速公路交通流特性，高速公路路段的运行最高速度一般情况下不得超过现行规范设计最高车速120km·h-1，拥堵路段运行(主线)的最低速度一般不得低于60km·h-1.考虑到交通安全和可变限速控制效果，相邻路段运行速度的差异值控制在20km·h-1之间，综合以上分析，可变限速控制模型的约束条件如下：

1)路段的运行速度范围控制值 ：60km·h-1≤ui(k)≤120 km·h-1;

2.3 模型校准

为了提高模型适应性，根据VISSIM仿真交通数据对模型进行校准.首先,确定交通特征参数Qmax=1 700 辆·车道-1h-1、w=11.5 km·h-1、ρc高峰=40辆·车道-1h-1、ρjam高峰=110辆·车道-1h-1、θ=15%；其次，确定模型参数向量β=[τ,υ,kkappa]，根据Matlab序列二次规划函数算法(sequential quadratic programming)对目标函数f(β)(式(8))求最小值，当预测值和仿真值之差最小时的参数，即为最优模型参数.

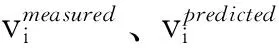
3 目标函数及模型验证指标

3.1 构造目标函数

为了达到最佳效果，同时考虑通过高速公路试验段总运行时间(车h)和总车公里数(车km)最优化，构造目标函数J(x,u).当仿真中函数J值达到最小值时，即总运行时间达到最小值且总交通量达到最大值时，预测值为最佳值，仿真进入迭代下一步.

式中:TTTT、TTTD分别为通过高速公路试验段总运行时间和总车公里数；αTTT、αTTD分别为TTTT和TTTD的系数；NP为仿真中总的时间步骤，其余符号意义同上文.

3.2 确定模型验证指标

为了进一步验证可变限速控制模型是否能起到预期效果，确定通过高速公路试验段总运行时间TTTT、通过试验段总车公里数TTTD、通过试验段总交通量TTF以及试验段Logistic事故率预测模型CP值四个指标对可变限速控制模型应用效果进行验证.TTTT和TTTD见式(9)，TTF公式如下：

式中:qi(k+j)为试验段第i个路段，第j个时间步骤通过的交通量.

构造Logistic事故率预测模型CP，模型的参数根据加拿大埃德蒙顿高速公路Whitemud Driver试验段(11 km)2010年8月份至2011年12月交通事故路段监测断面车速，进行Logistic回归分析(见表1).根据事故发生前10 min的数据样本分析结果，在交通流、占有率和车速差三个参数中，与事故率相关度最高的参数是车速差，为了更加精确表征车速差与事故率之间的关系，选择事故发生前5～10 min路段相邻车道的车速差均值和每个车道的车速标准差均值作为自变量，事故率作为因变量建立事故概率模型CP,如下所示.

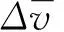
表1 Logistic事故预测模型回归参数值Tab.1 Regression parameter value of logistic accdicent modle

4 仿真及结果分析

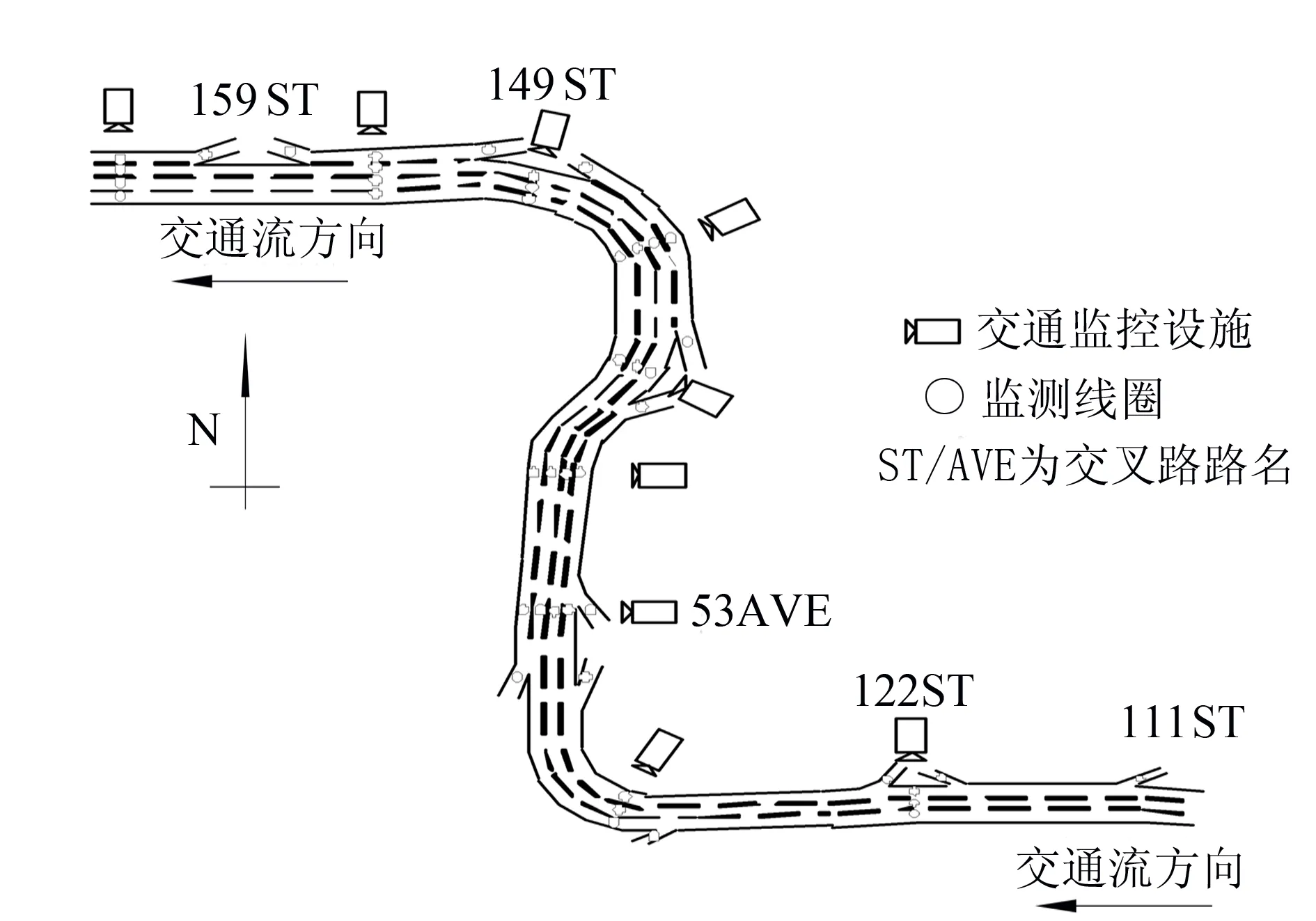
图4 仿真路段Fig.4 Simulation section

将加拿大阿尔伯塔省埃德蒙顿Whitemud Driver高速公路111ST-159ST路段选择为仿真对象，该路段设计车速110 km·h-1，长度约11 km,主线车道3～4个不等，有7个上匝道和6个下匝道，主线断面设有9个监测线圈，上下匝道出入口处各设有监控设施(具体见图4)，路段交通高峰期出现在下午4:00～6:00，年均日交通流大约40 000 pcu·h-1.

根据高速公路交通运行特性，确定可变限速车速变化时间间隔分别取5、3、2、1 min,每次车速变化量分别取5、10 、15 、20 km·h-1，按照不同时间间隔和变化量进行排列可组合成16种不同的场景，对每一种场景与无可变限速场景分析进行仿真结果对比，见表2和表3.

分析表2中数据可以看出，可变限速模型在不同场景中降低总运行时间28.6%～33.2%.在5、3、2、1 min四个变化频率中，10 km·h-1的变化幅度降低通过试验段高速公路总运行时间TTTT的效果最好，从无可变限速场景的1 002车h分别降低到668、669、676和685车h，降低了33.16%、33.15%、32.53%、31.59%.

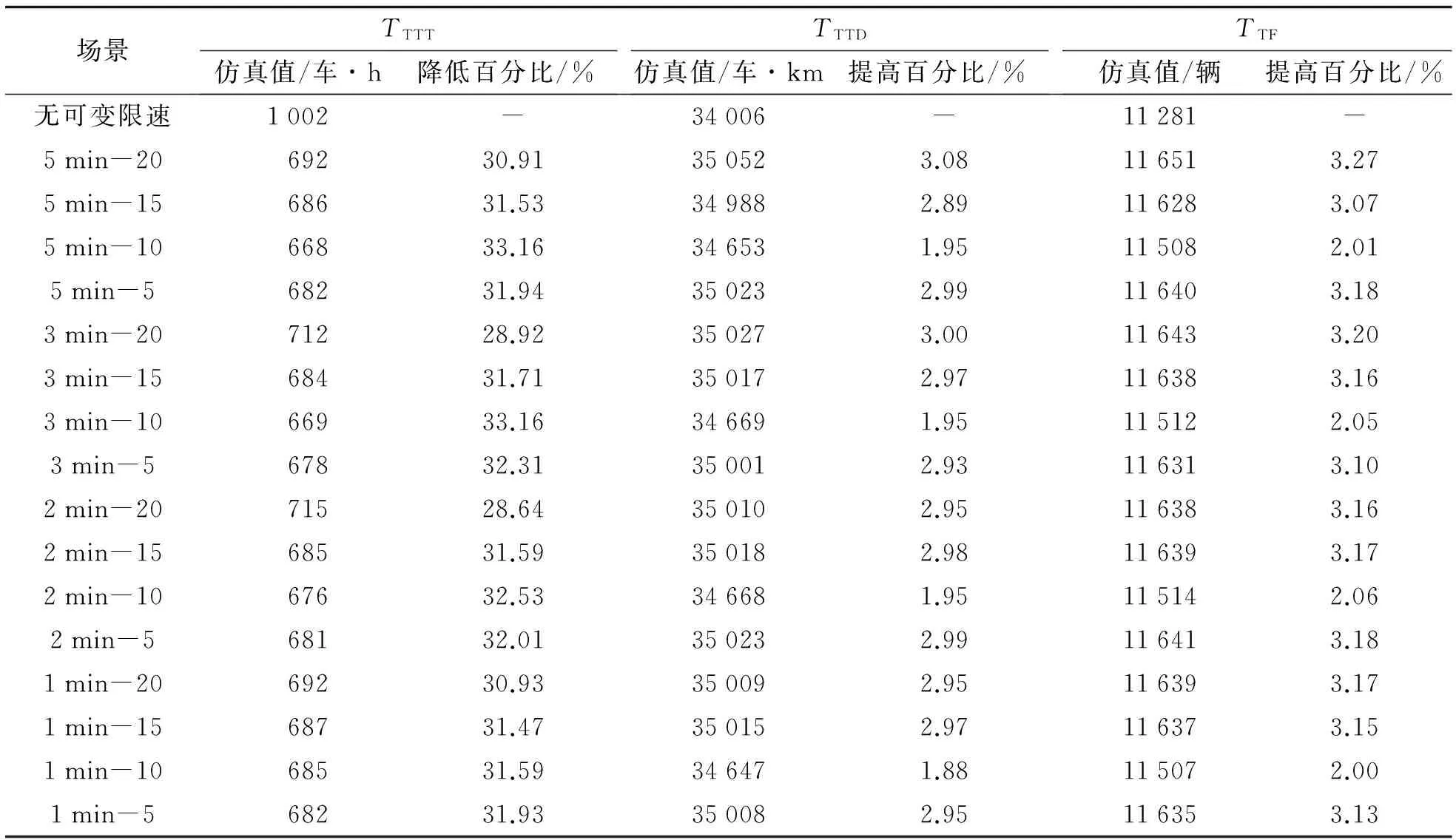
表2 可变限速控制模型应用效果Tab.2 Application effect of VSL control model

注：表中第一列中”5 min-20”，表示每间隔5 min速度限制值变化20 km·h-1，其他以此类推.

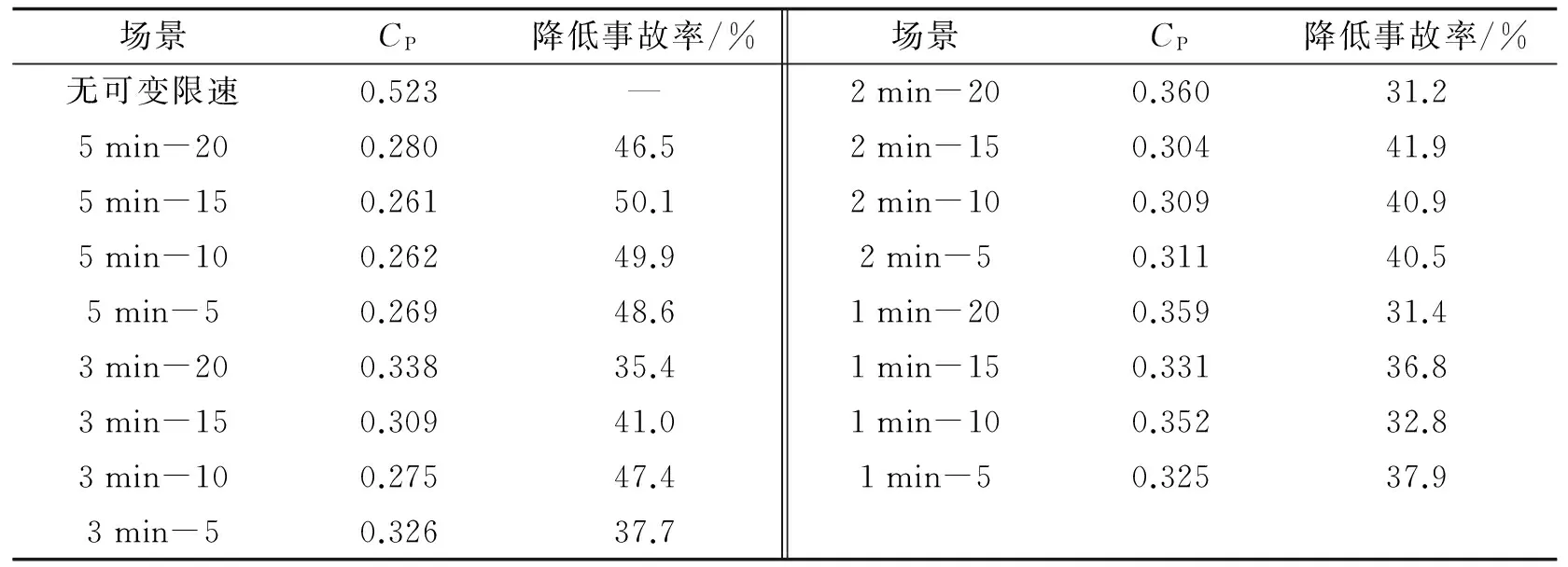
表3 可变限速阈值及变化频率仿真事故结果Tab. 3 Accident results of varied threshold value of VSL and interval frequency

注：表中第一列中“5 min-20”，表示每间隔5 min速度限制值变化20 km·h-1，其他以此类推。

可变限速模型在不同场景中提高通过试验段高速公路总车公里数1.8%～3.0%，总体上改善的效果不明显.在5 min和3 min变化频率中，20 km·h-1的变化幅度对提高TTTD的效果最好，从无可变限速场景的34 006车km分别提高到35 052车km和35 027车km，提高了3.08%和3.0%.在2 min和1 min变化频率中，提高TTTD效果最好的车速变化幅度分别为5 km·h-1和15 km·h-1，但是与其他档次的车速变化幅度相比提高的效果基本可以忽略不计，而提高TTTD效果最差的车速变化幅度为10 km·h-1.

可变限速模型不同场景中提高通过试验段高速公路的总交通量2.0%～3.27%，总体上改善的效果不明显.在5、3、1 min变化频率中，20 km·h-1的变化幅度对提高TTF的效果最好，分别从无可变限速场景的11 281辆提高到11 651、11 643和11 639辆，提高了3.27%、3.20%和3.17%.在2 min变化频率中，除了10 km·h-1的变化幅度效果较差外，其他三个变化幅度对TTF的影响基本相当.分析表3中数据可以看出，可变限速变化频率取5 min时比3、2、1 min的变化频率对降低交通事故率的效果更好，这一结果说明如果车速变化太频繁反而导致交通安全水平降低，与前人的研究结论一致.

在可变限速变化频率5 min的四个场景中，15 km·h-1和10 km·h-1变化阈值得到基本相当的结果，降低事故率分别为50.1%和49.9%，而当变化阈值增大到20 km·h-1时，降低事故率46.5%，表明效果反而不好.

综合以上分析，仿真结果中模型验证指标TTTT、TTTD、TTF以及CP的变化情况，表明可变限速控制模型是有效的，为了充分保障交通安全水平，可变限速变化阈值取10 km·h-1及变化频率取5 min是合适的,在该组合下可变限速策略可以达到较佳的效果.

5 结论

针对可变限速控制策略核心模块中的可变限速预测模型适应性和可变限速阈值及变化频率确定问题，提出可变限速修正模型，并应用仿真对模型进行验证和应用效果分析.加拿大Whitemud Driver高速公路试验段仿真结果表明修正模型在应用中可降低总运行时间28.6%～33.2%，提高总车公里数1.8%～3.0%，提高总交通量2.0%～3.27%；可变限速变化阈值取10 km·h-1及变化频率取5 min时的组合效果可降低交通事故率约50%，效果最佳，说明可变限速修正模型适应性较好，在仿真应用中能达到预期的效果.

[1] LEE C,HELLINGA B,SACCOMANNO F F.Evaluation of variable speed limits to improve traffic safety[J].Transportation Research Part C,2006,14(3)：213-228.

[2] ALLABY P,HELLINGA B,BULLOCK M.Variable speed limits:safety and operational impacts of a candidate control strategy for freeway applications[J].IEEE Transactions on Intelligent Transportation Systems,2007,8(4):671-680.

[3] ABDEL-ATY M,DILMORE J,HSIA L.Applying variable speed limits and the potential for crash migration[J].Transportation Research Record:Journal of the Transportation Research Board,2006,1953(1):21-30.

[4] HADIUZZAMAN M,QIU T Z,LU X Y.Variable speed limit control design for relieving congestion caused by active bottlenecks [J].Journal of Transportation Engineering,2013,139(4):358-370.

[5] GUEBERT A A,CHOW R,MULYK C,etal.Variable speed limits framework on a pilot study on alberta highways[C]// Conference and Exhibition of the Transportation Association of Canada:Transportation-An Economic Enabler.Fredericton:Innovations and Opportunities，2012:624-647.

[6] 张乐飞.高速公路瓶颈路段可变限速控制方法研究[J].北京交通大学学报,2012,36(5):78-83.

[7] 李志斌，刘攀，单肖年，等.高速公路可变限速控制策略安全性效果仿真[J].西南交通大学学报，2013,48(5):942-948.

[8] 蒲云，胡路，蒋阳升,等.高速公路主线收费站可变限速控制[J].交通运输工程学报，2012,12(5):119-126.

[9] PAPAGEORGIOU M,BLOSSEVILE J M,HADJ S H.Macroscopic modeling of traffic flow on the boulevard peripherique in Paris[J].Transportation Research (Part B)，1989,23(1):29 -47.

[10] HADIUZZAMAN M.Variable speed limit control to mitigate freeway congestion[D].Edmonton:The University of Alberta,2014.

(责任编辑：林晓)

The optimization of variable speed limits control model on freeway

WU Dehua,LIN Yi

(College of Civil Engineering,Fuzhou University,Fuzhou,Fujian 350116,China)

To settle the drawback of basic METANET model while be applied on freeway congestion section,the paper revised the speed model and flow model and proposed the modification VSL model of freeway,also figured out the varied threshold value of VSL and varied interval frequency.The proposed model was calibrated and validated by simulation.The simulation results shown that the proposed control can decrease total travel time by 28.6% to 33.2% and promote the total travel distance about 1.8%～3.0%,increase the total flow about 2.0% to 3.27%,which proved that the modification model was adapt and effective in implement.Also,the results shown that the most benefit can be got while the variable threshold value of VSL was 10 km·h-1and variable interval frequency was 5 minute,which can reduce 50% traffic accidents.

freeway; variable speed limits model; simulation; speed limit threshold; speed limit change frequency

10.7631/issn.1000-2243.2017.02.0216

1000-2243(2017)02-0216-06

2015-11-24

吴德华(1978-)，副教授，主要从事交通规则与交通安全方面研究，wudehua2000@163.com

福建省自然科学基金资助项目(2016J01230)；

U491.2

A