GM-LSSVM模型在建筑能耗预测中的应用

吴炜洪，许巧玲，严哲钦，林跃东

(福州大学石油化工学院，福建 福州 350116)

GM-LSSVM模型在建筑能耗预测中的应用

吴炜洪，许巧玲，严哲钦，林跃东

(福州大学石油化工学院，福建 福州 350116)

为提高大型公共建筑能耗的预测精度，提出一种基于灰色模型和最小二乘向量机方法(GM-LSSVM)的办公能耗预测模型.该方法结合灰色建模计算简单的特点，以及最小二乘支持向量机非线性拟合能力和泛化能力强的优势，充分发掘样本数据的规律,并以粒子群优化算法进行模型参数选择.根据福州某大型公共建筑能耗数据，通过本研究提出的方法建立预测模型，并与神经网络模型以及最小二乘支持向量机模型的预测结果进行比较，验证了该方法具备较高的预测精度和较强的泛化能力.

公共建筑；能耗预测模型；灰色模型；最小二乘支持向量机；粒子群优

0 引言

伴随着我国经济快速发展，大型公共建筑面积持续增长，大型公建作为用能大户，其能耗问题受到广泛关注.对于已有的大型公共建筑，由于其用能方式、人员节能意识与习惯、管理制度等方面的原因，造成大型公共建筑实际运行过程中能源消耗严重浪费.因此，针对大型公建的能耗预测和用能定额研究具有重要意义.

近年来，针对建筑用电量、用水量等能耗预测的理论和方法不断涌现，如灰色预测法[1-2]、线性回归分析[3-4]、人工神经网络[5-6]、支持向量机的预测方法.灰色预测模型(grey model，GM)具有建模简单、所需样本数据少、计算简便的优点，但是灰色建模方法对于具有非线性特性的能耗预样本预测效果欠佳.多元线性回归预测方法由于模型结构简洁，因此在建筑能耗领域得到了广泛应用.然而，多元线性回归预测方法的不足之处在于，其对历史数据要求高，对于非线性系统需要人为确定模型参数，且预测精度不高.虽然人工神经网络具有很强的学习能力和非线性函数拟合能力，对建筑几何参数或热参数要求低，适用于各类建筑能耗及设备节能改造分析，但其存在着收敛速度慢，容易陷入局部极值和过拟合等缺陷，导致能耗预测结果不理想.

支持向量机(support vector machine，SVM)是统计学理论的一种新型机器学习方法，建立在结构风险最小化原理的基础上.与传统建模方法相比，成功克服了“维数灾难”和“过学习”问题，具有泛化能力强、全局最优和对样本维数不敏感等优点，所需训练数据少，可以高效建立模型解决非线性问题，因此,近年来被广泛应用于建筑能耗预测和分析[7-8].本研究选用支持向量机的改进方法—最小支持二乘向量机(least squares support vector machine，LSSVM)应用于建筑能耗预测中.与SVM相比，LSSVM在求解速度和收敛精度方面变现更加优秀，增加能耗预测精度.

尽管国内外对于建筑能耗预测有许多的研究，但是能耗系统作为一个典型的具有多变量、强耦合和不确定特性的复杂动态系统，对其进行精确建模仍然具有较大的困难.究其原因，一方面，是室外气候、太阳辐射等变化.另一方面，是室内结构规划、人们用能习惯、调控温湿度等.这些因素之间存在着非线性和较强的相关性，导致模型预测结果不理想，降低预测精度.

为提高建筑能耗预测模型的精度和可靠性，本研究结合灰色建模所需样本数据较少和最小二乘支持向量机求解非线性强的优点，提出GM-LSSVM的建筑能耗组合预测方法.首先，将建筑能耗的原始数据进行灰化预处理，弱化样本的波动性和随机性，增加训练样本的规律性，提高预测精度.为避免最小二乘支持向量机的正规化参数γ和核宽参数σ2选择的主观盲目性，利用粒子群算法的全局寻优能力对LSSVM的参数进行优化选取，进一步提高了模型的预测精度和泛化能力.最后，通过仿真试验证明该模型在建筑能耗预测中具有较强的泛化能力和较高的预测精度，为大型建筑用能定额提供重要的依据，提高能源利用率，并为建筑能耗在线预测奠定了基础.

1 GM-LSSVM模型方法

1.1 灰色模型(GM)

灰色系统[9-10]通过对原始数据挖掘和整理来提高模型预测精度，主要特点是使用的不是原始数据序列，而是生成新的数据系列，再用微分方程建模.建筑能耗具有一定的周期性，各影响因子之间相互作用且关系不明确，具有灰色特征，可将灰色系统应用于能耗建立预测模型[1-2].常用的G(1,1)模型是由单一变量一阶微分线性方程构成的，其主要步骤如下：1)对原始数据进行一次累加生成(1-AGO)，弱化随机序列的波动性和随机性; 2)建立一阶时间响应微分方程，采用最小二乘法求其参数，确定时间响应方程; 3)对输出数据进行一次累减生成处理(IAGO)，得到预测结果.

1.2 最小二乘支持向量机(LS-SVM)

最小二乘支持向量机用等式约束取代了SVM中的不等式约束，将SVM的损失函数转化为LS-SVM的误差平方和，求解线性方程组从而有效避免求解SVM二次规划问题，加快了求解速度[11-12].

对于给定的训练样本(xi,yi)(xi为第i个输入量，xi=[xi(1),xi(2),…,xi(h)]；yi为与之相对应的输出量)，经过非线性映射函数φ，将非线性问题转变为高维特征空间的线性问题，其特征空间优化问题和约束条件：

式中：γ为正规化参数；ek为误差；b为偏置.

构造拉格朗日函数进行优化求解：

式中：βk为Lagrange算子.根据Karush-Kuhn-Tucker进行优化：

上式化解得出矩阵方程：

式中：

对上式进行求解得出b和β，则LSSVM回归模型：

1.3 粒子群优化算法(PSO)

正规化参数γ和高斯核函数σ2取值不当容易发生“欠学习”或者“过学习”，对LSSVM的泛化能力和预测效果有非常大的影响.粒子群优化(PSO)算法通过当前搜索到的最优值寻找全局最优值，具有参数少，收敛速度快，运算简单、易于实现等优点.因此，本研究运用粒子群算法优化选取LS-SVM参数，提高模型预测精度.

在整个群体中，每一代粒子根据公式(7)和(8)更新速度和位置，最终找到最优值.

其中：k表示当前迭代次数；Qid表示粒子速度；Pid表示粒子位置；c1,c2表示学习因子；r1,r2表示分布于[0，1]的随机数；ωk表示粒子惯性权重.

本研究中优化LSSVM模型的参数可以看作是应用粒子群算法处理连续优化问题，从而找出最优的正规化参数和高斯核函数(γ,σ2)组合，使目标函数达到最小值.优化问题的目标函数为：

优化过程的主要步骤为：

1)随机初始化粒子群，包含群体规模，每个粒子的位置和速度；

2)计算每个粒子的适应度值；

3)根据每个粒子的适应度，选择最优个体极值和群体极值；

4)根据公式(7)、(8)更新粒子速度和位置；

5)判断是否达到最大迭代步数或满足最小误差标准，是者退出得到最优解，否者回到步骤2).

2 建立GM-LSSVM能耗预测模型

大型办公建筑能耗预测是指利用历史能耗数据和相关影响因素，对未来时刻能耗估计值的预测.建筑能耗影响因素复杂，具有非线性等特点，较难寻找到其规律性[13-14].采用灰色-最小二乘支持向量机组合预测方法，并采用粒子群算法对预测模型关键参数进行优化处理.预测模型借助灰色理论方法对原始数据(包括能耗影响因素及能耗值)进行累加处理，将无规律的离散数列变成有规律的序列，有效地弱化数据的波动性.然后，利用改善过后对非线性数据具有高效处理能力的最小二乘支持向量机建立预测模型，并根据评价指标进行评价.GM-LSSVM建筑能耗预测流程图如图1所示.

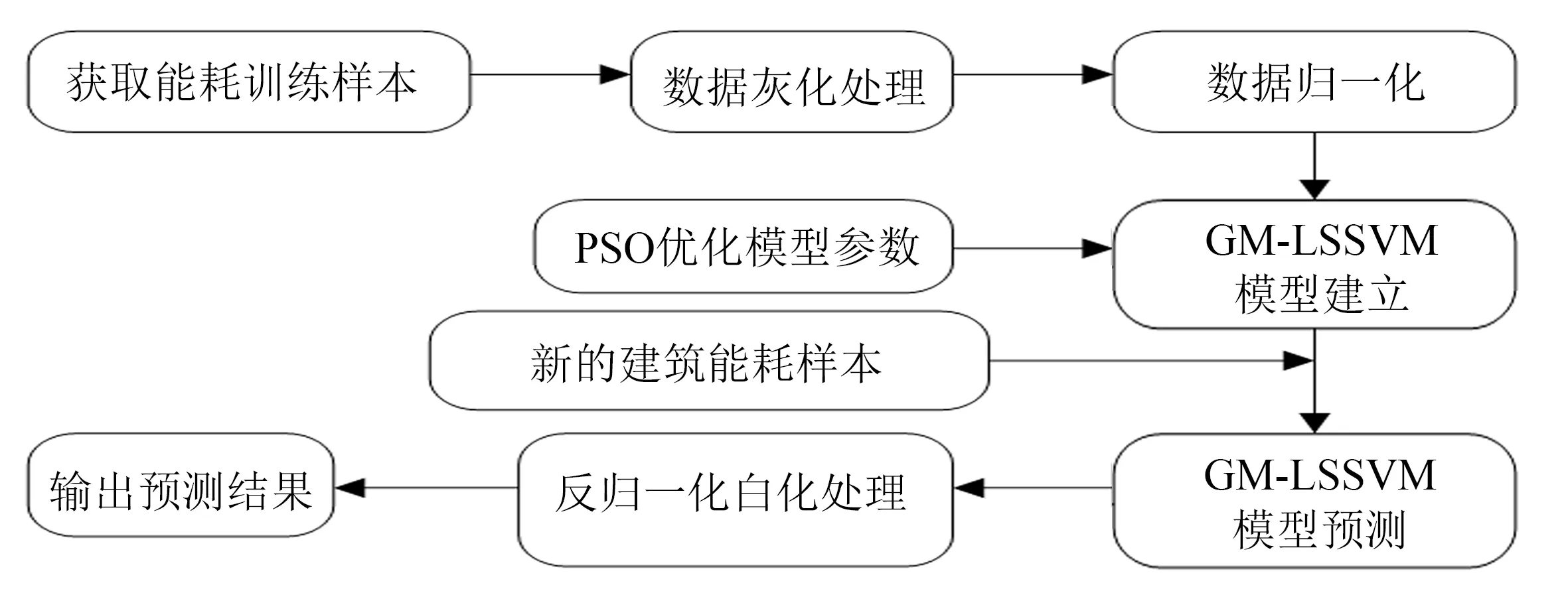
图1 GM-LSSVM能耗预测方法流程图Fig.1 Sketch of the energy consumption for GM-LSSVM

基于PSO优化的GM-LSSVM建模步骤如下：

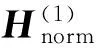
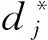
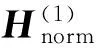
4)建立GM-LSSVM模型.根据步骤3)得出的最优参数γ和σ2，按式(4)求解b和β，建立GM-LSSVM模型.

训练LS-SVM模型的关键问题在于参数的选取，即正规化参数γ、核函数类型及核参数，选择合适的参数有利于模型的泛化能力、训练速度和预测精度.基于径向基核函数(RBF)的LS-SVM模型适用于多种条件下，收敛域较宽，是较为理想的核函数.因此，本研究选用径向基核函数：

3 实例分析

3.1 实例分析1

本研究对我国南方某大型政府办公建筑的逐日能耗量进行预测，验证所提出的GM-LSSVM建筑能耗预测模型的可行性.此办公建筑采用钢筋凝土框架-筒体结构，16楼层高度及一层地下室，并配有一栋3层的附属楼，建筑总面积约为19 700m2，大楼总高度为57.4m，地上建筑面积17 315.62m2，地下建筑面积2 384.88m2，标准层层高3.5m.外墙传热系数1.71W·m-2·K-1，屋面传热系数1.31W·m-2·K-1，楼板传热系数2.49W·m-2·K-1，外窗传热系数5.70W·m-2·K-1.本建筑因某些特殊科室使用情况差异采用分体式空调外，其余科室均使用中央空调进行采暖制冷.该办公建筑人员实行双休制度，节假日安排同国家法定节假日一致，放假期间，除保证建筑功能正常运行的用电器运行之外，其他用电设备停止使用.

所研究的建筑地处亚热带地区，夏季和冬季有明显差别.夏季炎热冬季湿冷，导致人们用能习惯因为季节的改变而变化，对空调的需求最为显著.而大型建筑中暖通空调用能对建筑总用能影响严重，因此，针对该地区建筑能耗的季节性分布特点[15-17]，对所选建筑的能耗进行预测.

3.1.1 参数选择

大型建筑能耗的影响因素主要有：外部气候、城市微气候、建筑规划、维护结构热工特性和建筑使用功能及人为因素.对于已建成的大型办公建筑，其建筑规划和维护结构、材料已经固定，建筑内各部门使用功能明确，因此，对建筑能耗的变化影响较小，本文忽略不计[17].外部气候、城市微气候等对建筑环境产生影响，进而引起建筑内部温度、湿度变化，导致建筑能耗发生变化；法定节假日将导致空调、照明等系统停止或降低，影响建筑能耗[18-19].

为避免模型预测中出现过拟合现象，选用对预测输出量有较大关联性的参数，以最高温度X(1)、最低温度X(2)、天气特征X(3)、日平均风速X(4)、日平均湿度X(5)、是否工作日X(6)(其中工作日为0，非工作日为1)6个建筑能耗影响因子作为输入变量，与之相对应的建筑能耗Y作为输出量，建立组合预测模型*http://www.wunderground.com.其中，天气特征X5用特征值表示，如表1所示.

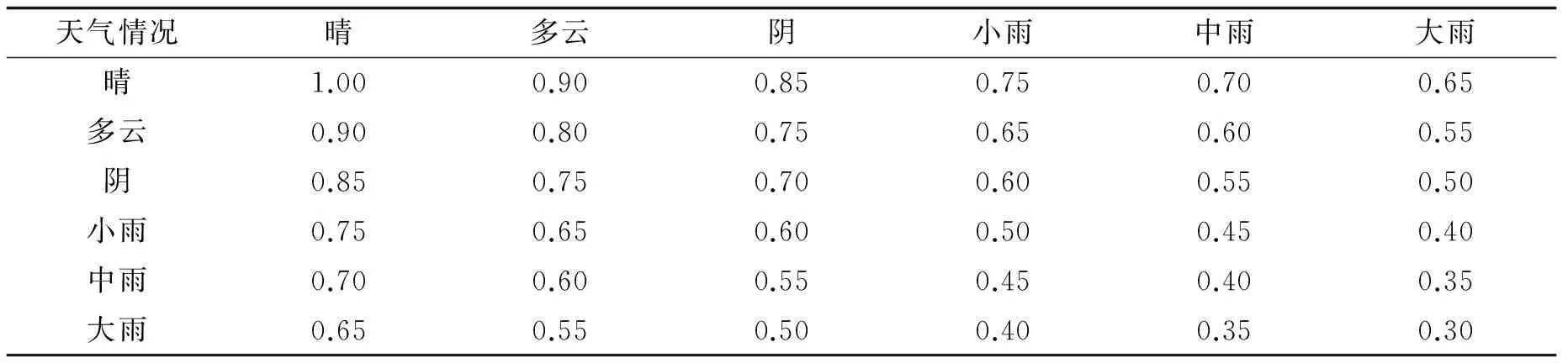
表1 天气特征值数值表Tab.1 The weather characteristics numerical value

3.1.2 样本数据

所研究的建筑都已建成大型建筑监测平台并投入使用，运行正常，可以实时在线采集数据,并提供历史能耗数据.选取历史能耗数值，保证原始数据来源的可靠性和真实性，尽可能减少能耗预测过程中的影响因素，提高模型预测精度.选取此办公建筑6、7月份(共61组样本数据)的历史能耗值作为试验数据，其中，前45组逐日样本数据作为模型训练数据，后16组逐日样本数据作为模型的预测验证数据，检验模型的预测能力.

3.1.3 评价指标

采用平均相对误差MRE、平均绝对误差MAE和均方根误差RMSE三个性能指标对上述4种预测模型进行考核评估，得到相应的性能指标.

3.1.4 结果与分析

根据所提出的GM-LSSVM建模步骤，61组原始数据作为训练样本和预测样本，建立能耗动态组合预测模型.为比较组合模型预测效果，同时建立了能耗RBF模型和LSSVM模型.这3种模型的逐时拟合输出与实际值比较如图2所示，逐日预测输出与实际值的比较如图3所示.粒子群算法快速确定了LS-SVM的2个参数，最终结果为：γ=8.32、σ2=2.31，满足了预测模型对精度的要求.

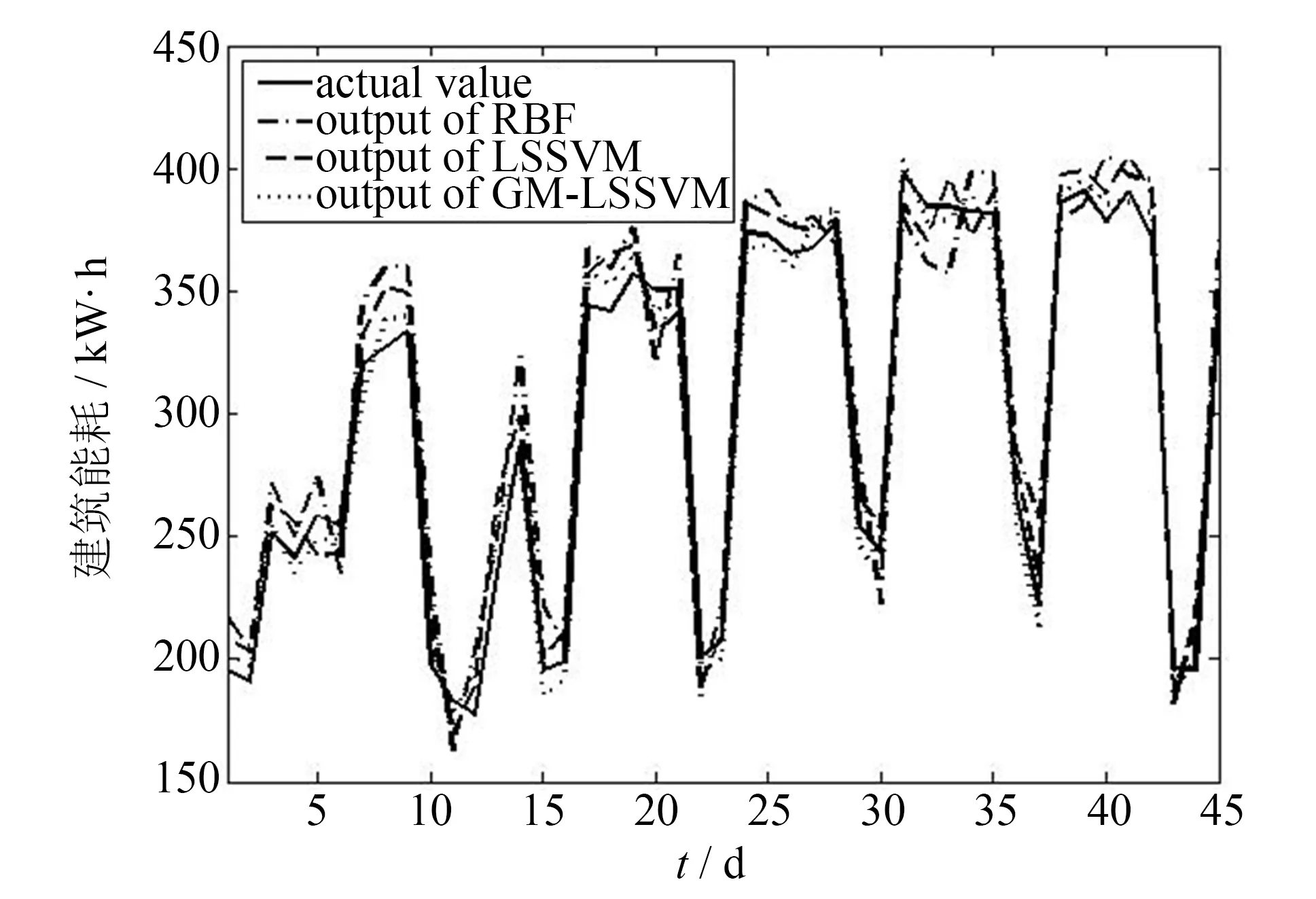
图2 三种办公建筑能耗模型拟合结果比较Fig.2 Fitting of three office building energy consumption models

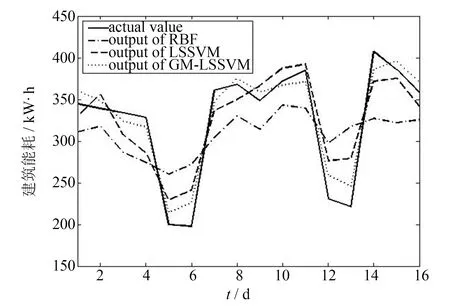
图3 三种办公建筑能耗模型预测结果比较Fig.3 Prediction of three office building energy consumption models

从图2可以看出，三种模型都能较好地拟合出大型办公建筑的能耗模型，其中本研究采用的GM-LSSVM拟合相对误差最小为2.8%，体现出了组合预测模型具有较强泛化能力及非线性拟合能力.从图3可以看出，这3种方法的预测结果都在一定程度上表现出能耗的变化趋势.相对单一的RBF模型和LSSVM模型，GM-LSSVM模型的预测输出结果更接近实际值.

这3种模型对训练样本数据拟合和对测试样本数据预测的绝对误差(MAE)、相对误差(MRE)和均方根误差(RMSE)的计算结果如表2.

表2 办公建筑能耗模型结果误差指标比较Tab.2 Comparison of office building energy consumption models

通过对图3，表2的对比分析可知，RBF方法虽然拟合效果不错，具有较好的模拟训练精度，但是当用于预测时，个别月份误差较大，预测效果不理想.LSSVM模型对于能耗的非线性特征有较理想的处理，相比于RBF神经网络模型具有更好的预测效果，但是预测结果仍然有待提高.结果表明，本研究采用的GM-LSSVM组合预测模型的平均相对误差比单一的神经网络模型和单一最小二乘支持向量机模型平均降低了6.10%.一方面是因为GM-LSSVM组合预测模型通过对原始数据进行灰色处理，加强了数据规律性，弱化了随机波动性；另一方面是采用了粒子群优化算法对LSSVM的参数进行优化选取，提高了预测准确度.相比于LSSVM模型，平均绝对误差从33.4降低到17.2，均方根误差也从36.8降低到19.3，表明参数优化后的组合预测模型具有更高的预测精度和预测稳定性，更加适用于建筑能耗建模预测.

3.2 实例分析2

为验证所提出的GM-LSSVM能耗预测模型对不同类型的大型建筑能耗预测的有效性，选取福州某高校图书馆(大型公用建筑)的逐日能耗数据再次进行模型验证.

选取该公用建筑2014年11、12月份和2015年1月份的逐日历史能耗数据进行验证，其中11、12月份(共61个样本数据)的建筑能耗值作为训练样本，而1月份(共31个样本数据)的建筑能耗值作为验证数据，分别建立建筑能耗RBF模型、LSSVM模型和GM-LSSVM组合模型，以比较3种模型的预测效果.这3种模型拟合值和实际值的比较如图4所示，逐日预测值和实际值的比较如图5所示.误差比较如表3所示.

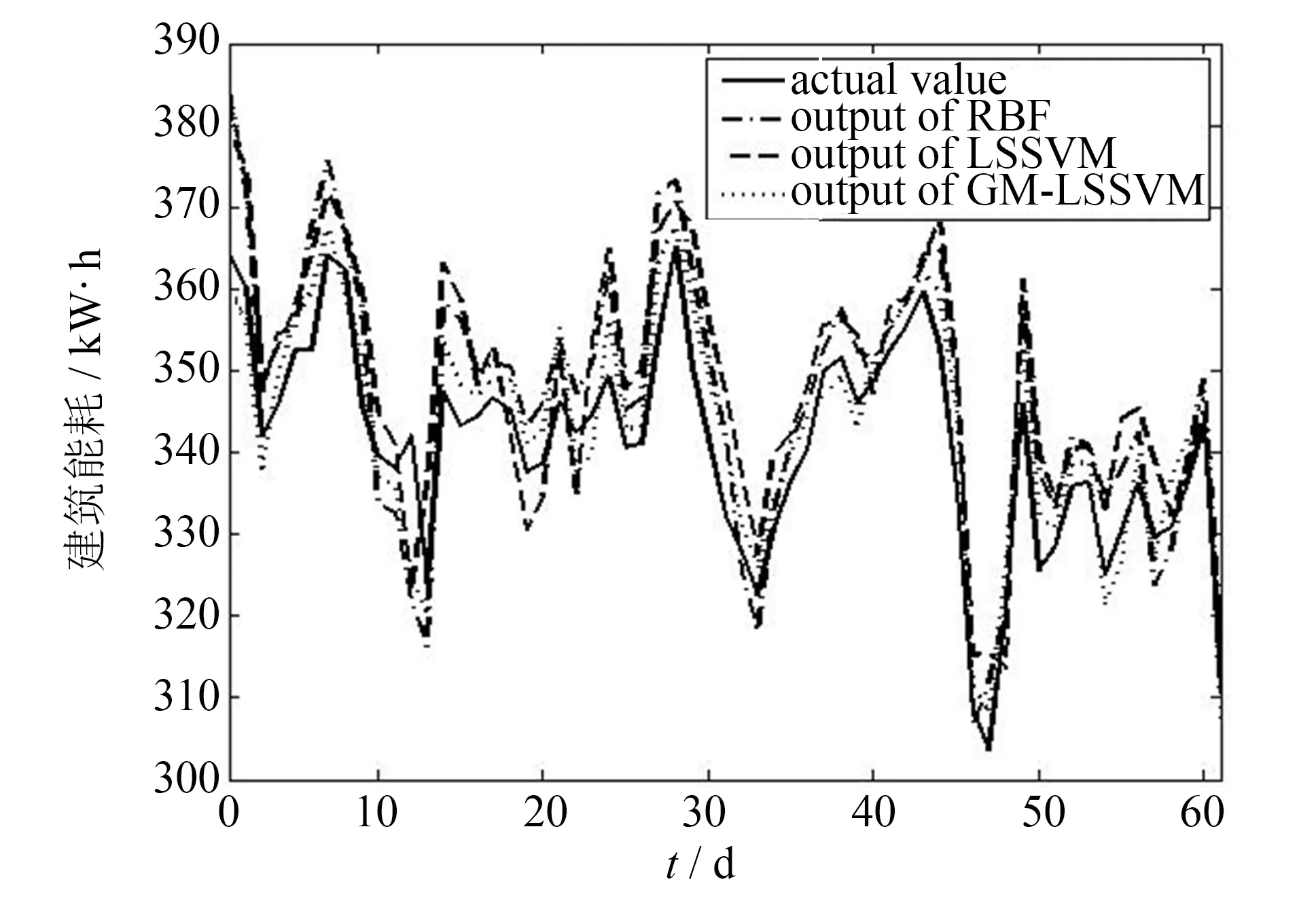
图4 三种公用建筑能耗模型拟合结果比较Fig.4 Fitting of three office public energy consumption models

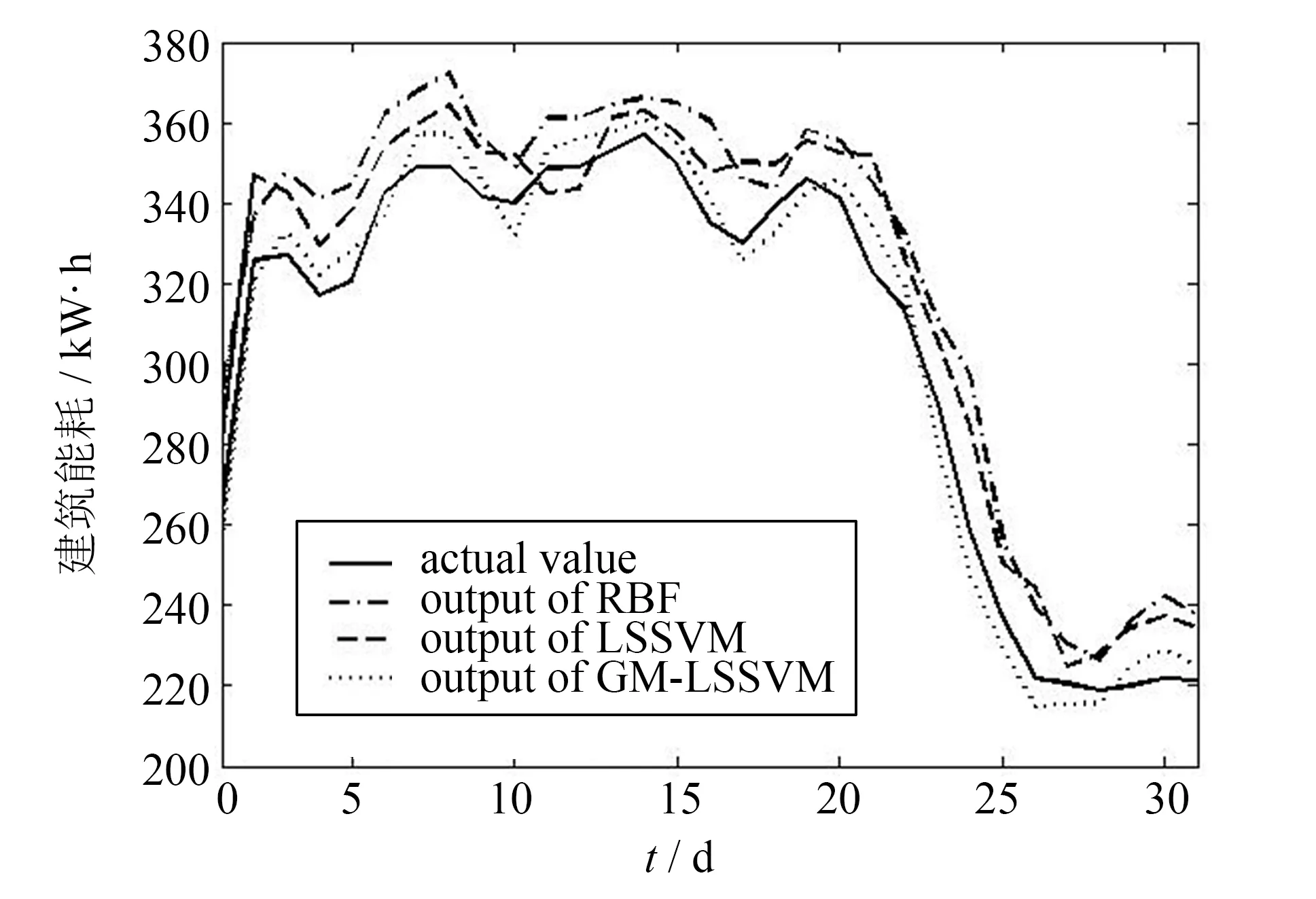
图5 三种公用建筑能耗模型预测结果比较Fig.5 Prediction of three public building energy consumption models

表3 公用建筑能耗模型结果误差指标比较Tab.3 Comparison of public building energy consumption model

从图4、图5可以看出，实例2中的建筑能耗成不规则波动趋势，符合所研究建筑为大型公用建筑用能特性，即工作日因素对建筑用能影响较小，明显区别于实例1的办公建筑用能成周期性震荡趋势.3种模型对于非线性的公用建筑能耗也能有较好的拟合能力，其预测结果在一定程度上能较好地跟随建筑能耗变化趋势，相比于RBF模型和LSVM模型，GM-LSSVM组合模型预测值最接近实际能耗值.

从表3的计算结果可以反映出，RBF模型同样反映出对于非线性函数有较好的拟合能力，但是预测效果不够理想.GM-LSSVM模型预测的评价指标都低于RBF模型和LSSVM模型的预测结果值.表明了所提出的组合能耗预测模型不仅在办公建筑能耗预测中，而且在公用建筑中同样具有较强的适用性.

4 结语

上述建筑能耗预测实例中，通过3种模型的预测结果及性能指标比较分析，GM-LSSVM软测量模型在建筑能耗中具有较强的可行性和实用性.

1)将所提出的建模方法应用于办公建筑和公用建筑的逐日能耗预测中，该组合预测模型方法相比于办公建筑能耗预测结果，其平均绝对误差相对RBF模型和LSSVM模型分别降低了7.9%和4.3%；在与公用建筑的预测模型比较中，相对于RBF模型和LSSVM模型分别降低了8.9%和3.9%.表明该组合预测模型具有较高的预测精度和良好的泛化能力，为大型建筑用能定额提供重要的依据，提高能源利用率，并为建筑能耗在线预测奠定了基础.

2)所提出的组合预测模型有效地结合单一灰色模型以及最小二乘支持向量机模型优点，相对于单一的预测模型有更高的预测精度以及泛化能力.

[1] WANG X,CHEN Z,YANG C,etal.Gray predicting theory and application of energy consumption of building heat-moisture system[J].Building and Environment,1999,34(4):417-420.

[2] GUO J J,WU J Y,WANG R Z.A new approach to energy consumption prediction of domestic heat pump water heater based on grey system theory[J].Energy and Buildings,2011,43(6):1 273-1 279.

[3] LEI F,HU P.A baseline model for office building energy consumption in hot summer and cold winter region[C]// International Conference on Management and Service Science.北京:IEEE,2009:1-4.

[4] MA Y,YU J,YANG C,etal.Study on power energy consumption model for large-scale public building[C]// International Workshop on Intelligent Systems and Applications (ISA).武汉:IEEE,2010:1-4.

[5] YALCINTAS M.Energy-savings predictions for building-equipment retrofits[J].Energy and Buildings,2008,40(12):2 111-2 120.

[6] 季文娟,顾永松,冯乐.基于模糊神经网络的建筑能耗评估模型研究[J].建筑节能,2013,41(11):67-69.

[7] DONG B,CAO C,LEE S E.Applying support vector machines to predict building energy consumption in tropical region[J].Energy and Buildings,2005,37(5):545-553.

[8] 唐莉,唐中华,靳俊杰.最小二乘支持向量机 (LS-SVM)在短期空调负荷预测中的应用[J].建筑节能,2013 (2):56-58.

[9] 邓聚龙.组合预测方法在建筑能耗预测中的应用[M].武汉:华中理工大学出版社,1990.

[10] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].4版.北京:科学出版社,2010.

[11] 邓乃杨,田英杰.数据挖掘中的新方法——支持向量机[M].北京:科学出版社,2004.

[12] SUYKENS J A K,VANDEWALLE J.Least squares support vector machine classifiers[J].Neural Processing Letters,1999,9(3):293-300.

[13] 席晓晶.基于神经网络算法的建筑能耗预测系统研究[J].电脑编程技巧与维护,2016 (4):45-46; 54.

[14] 聂子航,于学军.基于多元线性回归的办公建筑电力能耗评估预测模型的设计[J].电子设计工程,2016,24(3):40-43.

[15] 涂书阳,苏醒,罗仲,等.上海市高校建筑节能改造整体需求和潜力分析[J].建筑节能,2016(8):100-104.

[16] 赵超,林思铭,许巧玲.基于 GM-RBF 神经网络的高校建筑能耗预测[J].南京理工大学学报(自然科学版),2014,38(1):48-53.

[17] 李雪飞,程海峰.合肥某高校图书馆空调能耗模拟及影响因素分析[J].山西建筑,2014,40(32):127-128.

[18] 季文娟,顾永松.基于 PSO-RBF 的建筑能耗预测模型研究[J].建筑节能,2015(11):109-112.

[19] 汪君,吴利瑞.基于 BP 神经网络模型的上海高校能耗预测研究[J].建筑节能,2015(1):92-97.

(责任编辑：沈芸)

Forecasting of building energy consumption based on grey theory and least squares support vector machine

WU Weihong,XU Qiaoling,YAN Zheqin,LIN Yuedong

(College of Chemical Engineering,Fuzhou University,Fuzhou,Fujian 350116,China)

In order to improve the predictive accuracy of the building energy consumption model,a hybrid of GM-LSSVM prediction model is established.This method combines the advantage of low computation demand of grey theory and the ability of nonlinear mapping of least squares support vector machine(LS-SVM),the historical building energy consumption information is extracted effectively,and particle swarm optimization(PSO)is used to select parameters of LS-SVM model.According to the energy consumption data of the public building in southern city,the GM-LSSVM is used to predict the building energy consumption.The results show that the proposed model has higher accuracy and stronger generalization ability than RBF model and LSSVM model.

public buildings; energy consumption prediction model; rey model(GM)；least squares support vector machine(LSSVM)；particle swarm ptimization(PSO)

10.7631/issn.1000-2243.2017.02.0238

1000-2243(2017)02-0238-08

2015-09-01

许巧玲(1956-)，教授，主要从事工业过程控制及节能技术研究，zhhqxu@fzu.edu.cn

国家自然科学基金资助项目(60804027；61374133)；中国人民银行福州中心支行科研专项资助项目(00411220)

TU831

A