多重四边环索-张弦穹顶屋盖索力张拉方案比选

张 超，余 立，许 莉，林 威

(1.福州大学土木工程学院，福建 福州 350116；2.福建省交通规划设计研究院，福建 福州 350002)

多重四边环索-张弦穹顶屋盖索力张拉方案比选

张 超1，余 立1，许 莉1，林 威2

(1.福州大学土木工程学院，福建 福州 350116；2.福建省交通规划设计研究院，福建 福州 350002)

以首个多重四边环索-张弦穹顶屋盖工程——福州海峡奥林匹克体育中心体育馆为工程背景，对不同索力张拉方案进行比较研究.建立三维有限元分析模型，采用降温法模拟索力张拉施工过程，对比分析不同索力张拉方案下屋盖结构的响应变化规律.分析结果表明，在张拉过程中，多重四边环索-张弦穹顶屋盖的内力和变形受索力张拉顺序影响较大，但是，最终受力及变形状态相差不大.针对张拉过程而言，方案1屋盖竖向变形、网格梁内力均比方案2更加合理.因此，考虑施工中屋盖结构的合理性，建议采用“外环索-中环斜索-内环斜索-张弦索”的索力张拉顺序.

多重四边环索；张弦梁；穹顶；索力张拉

0 引 言

四边形环索结构是一种结构新型体系，由网格梁、斜索、下撑钢管及四边形环向索构成，通过斜索的预应力张拉，使下撑钢管受力，提高改善网格梁结构的受力和变形性能[1].当结构跨度较大时，可同时设置张弦梁进一步提高结构受力性能，形成四边形环索-张弦梁组合结构.此结构具有线条简单明快、用钢节约、传力明确的特点.多重四边环索-张弦结构作为新型的穹支屋盖体系，首次被应用于福州奥体中心体育馆椭圆形屋盖[2].

多重四边环索-张弦结构为复杂的预应力索空间受力体系，在索力张拉中，屋盖结构受力和变形规律十分复杂[3].针对张弦结构的索力张拉顺序，国内外学者已取得了较多的研究成果.石开荣等[4]采用传统的顺序张拉法对某体育馆环形辐射状预应力张弦梁钢屋盖进行了分析,结果表明该结构较柔，导致了各拉索之间索力影响较大.其采用逆向分析思路比较了一阶段张拉、两阶段张拉及三阶段张拉的3 种张拉方案，分析结果表明采用三阶段张拉为最优方案.并指出对于柔性预应力钢结构应采用逆向分析思路进行仿真分析，有利于保证施工阶段结构的可靠度.王哲等[5]以东亚运动会团泊自行车馆弦支穹顶张拉分析为例，反分析找形的结果表明采用混合张拉方式最合理，即先预紧径向拉杆，再张拉环向索.

但是，已有索力张拉优化的研究成果大多分别针对张弦结构或穹支结构开展，目前尚无针对此类组合结构索力张拉方法的研究成果.由于多重四边环索-张弦结构是由四边环索和张弦梁结构组合而成，其拉索索力相互影响规律与单一张弦结构或穹支结构不同[6].因此，本研究以福州奥体中心体育馆椭圆形屋盖为工程背景，基于SAP2000 建立研究多重四边形环索-张弦屋盖结构的三维有限元模型，采用降温法进行索力张拉全过程模拟，探讨不同索力张拉方案对屋盖受力和变形的影响规律，研究适合此屋盖体系的索力张拉施工方法.

1 工程背景

福州奥体中心体育馆，为福州市奥体中心“一场三馆”的重要组成部分，建成后将成为福州市的标志性建筑，其侧立面如图 1所示.体育馆的屋盖根据跨度不同，分别采用多重环索预应力空间张弦梁结构和平面主次桁架结构.其中，综合比赛馆上空屋盖为椭圆形，跨度约97 m × 116 m，为国内首次采用四边形环索弦支-张弦组合结构体系，周圈混凝土柱作为屋盖结构的内支座.针对多重环索结构的研究即以此工程为研究背景.

综合比赛馆屋盖最高点标高为39.7 m，为四边形环索-张弦组合体系(如图2所示).整个屋盖体系由拉索体系、撑杆体系和网格梁三部分组成自平衡受力体系.拉索体系由三重四边形环索和张弦结构组成，其中斜索、环索、张弦索平面分布如图2(a)所示，图2(a)中，编号1～7为拉索.屋盖拉索均采用高强钢丝组成的PE成品索，拉索的截面尺寸及长度详见表1.

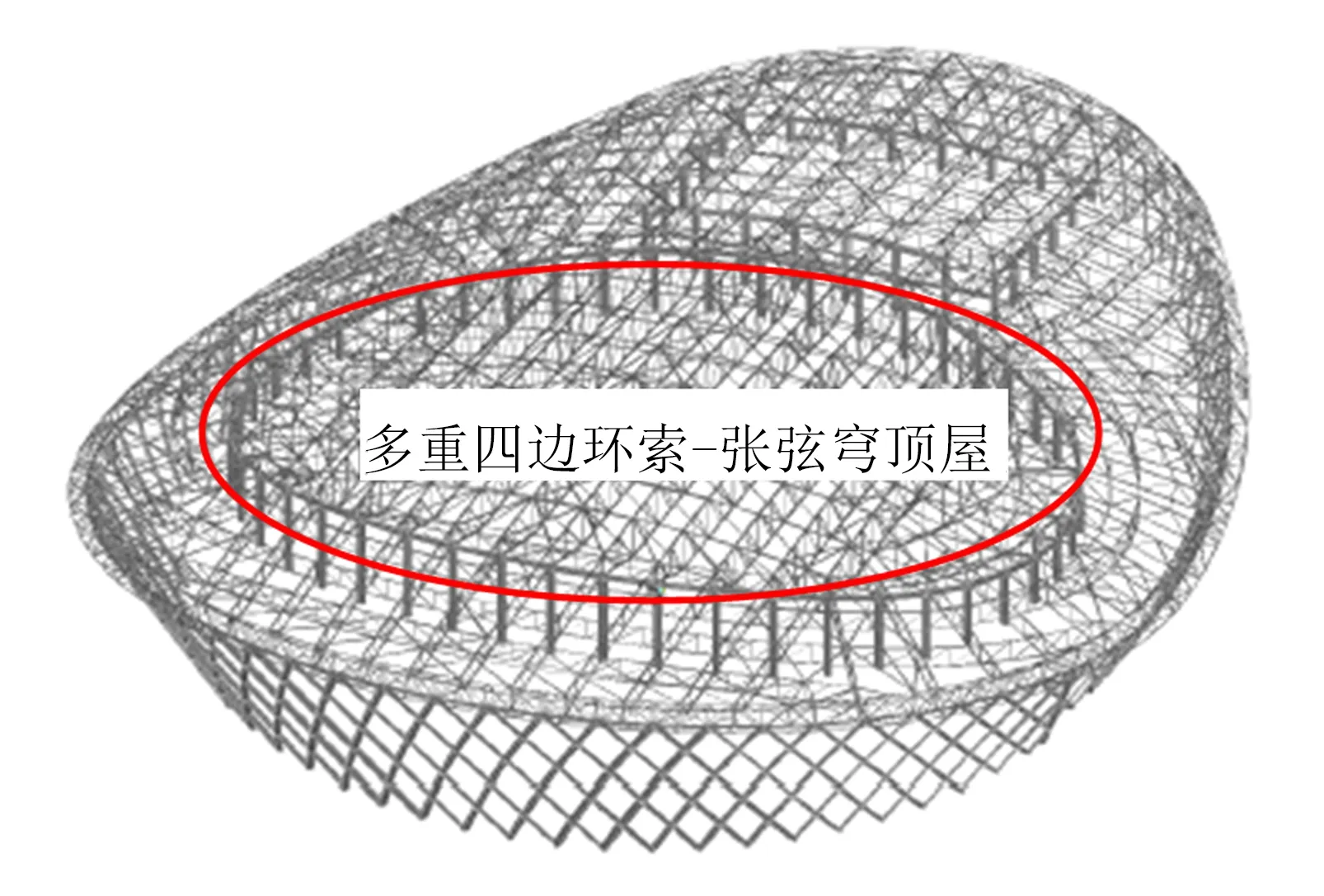
图1 福州奥体中心体育馆Fig.1 Fuzhou Olympic Gymnasium

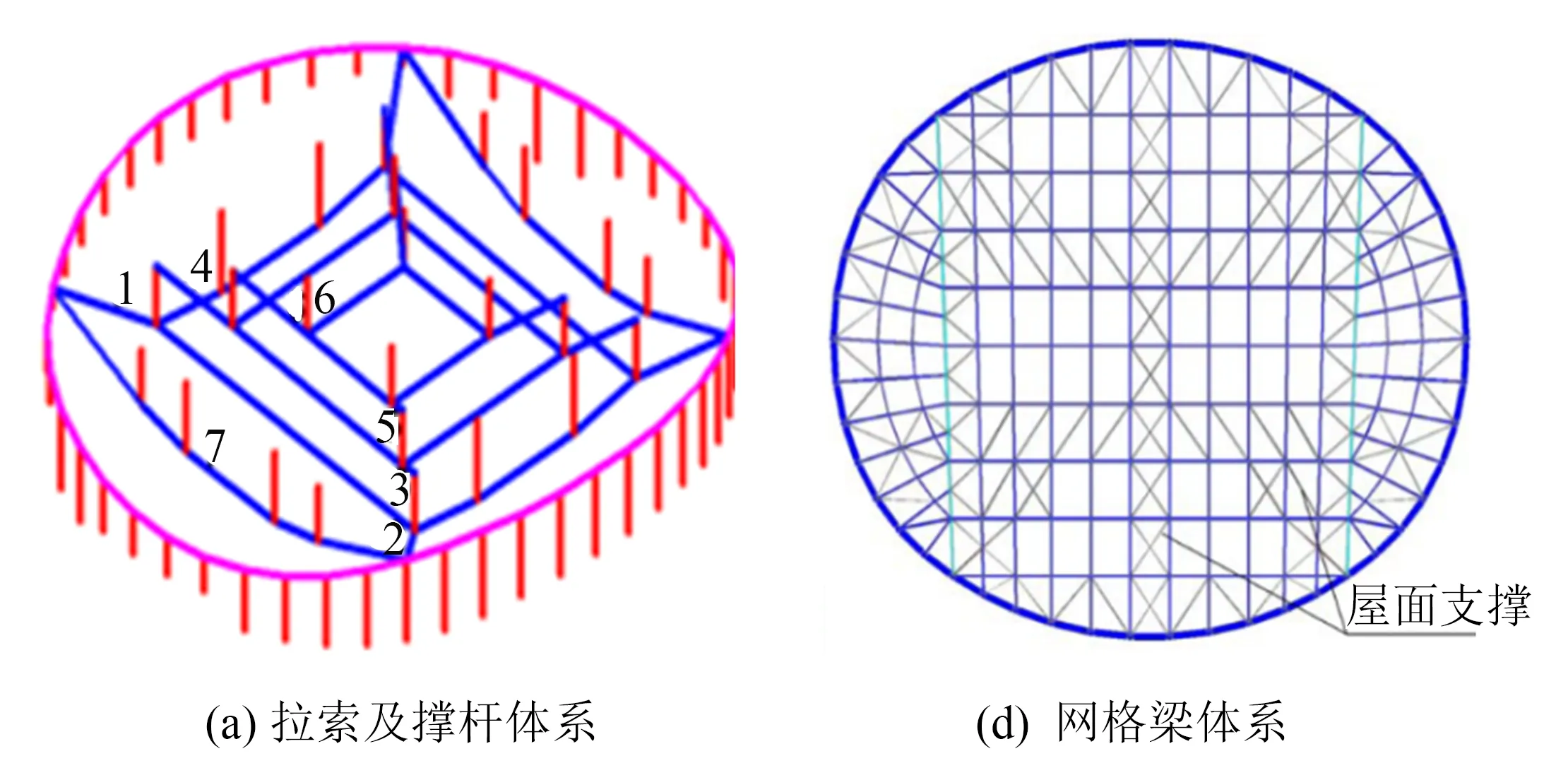
图2 四边形环索弦支-张弦屋盖Fig.2 Square loops-string dome

三重环索呈矩形环环相扣，第1 环(内环)撑杆高度9.0 m，四边形环索长21.6、19.0 m，斜索长13.9、15.0 m；第2 环(中环)撑杆9.0 m，四边形环索长37.9、36.0 m，斜索长13.4、14.85 m；第3 环(外环)撑杆9.5 m，四边形环索长56.9、51.1 m，斜索长度15.8、18.2 m.由于屋盖四边负荷面积较大，在外环索增设中间撑杆(高13.0 m)，并在东西两侧设置独立张弦结构(最大跨度75.9 m)，增加结构竖向刚度.撑杆采用Q345B型号钢材的矩形钢管制作，在每一环的顶点处各设置一根撑杆.为增强屋盖局部区域内的竖向刚度，在南北侧外环索和东西侧张弦索上分别增设两根撑杆.撑杆的截面及长度如表1所示.刚性网格梁结构的平面布置如图2(b)所示.网格梁主桁架最大跨度约97.5 m，主桁架间距从6.3到7.6 m不等.次桁架间距为9.5 m.网格梁由单层箱型截面组成，屋盖四周网格梁截面较大，跨中区域网格梁截面较小，最小箱型截面为B300 mm × 400 mm × 12 mm ×12 mm、最大箱型截面为B400 mm × 700 mm × 25 mm × 30 mm.屋盖中部正交网格尺寸为7.2～9.5 m，东西两侧采用放射状布置，网格尺寸5.5～8.5 m.为增强屋盖网格梁整体性，在屋盖周圈设置水平支撑，并沿屋盖纵向设置两道、横向设置一道水平支撑.撑杆截面尺寸为φ325 mm × 12 mm，φ351 mm × 14 mm，φ351 mm × 20 mm.

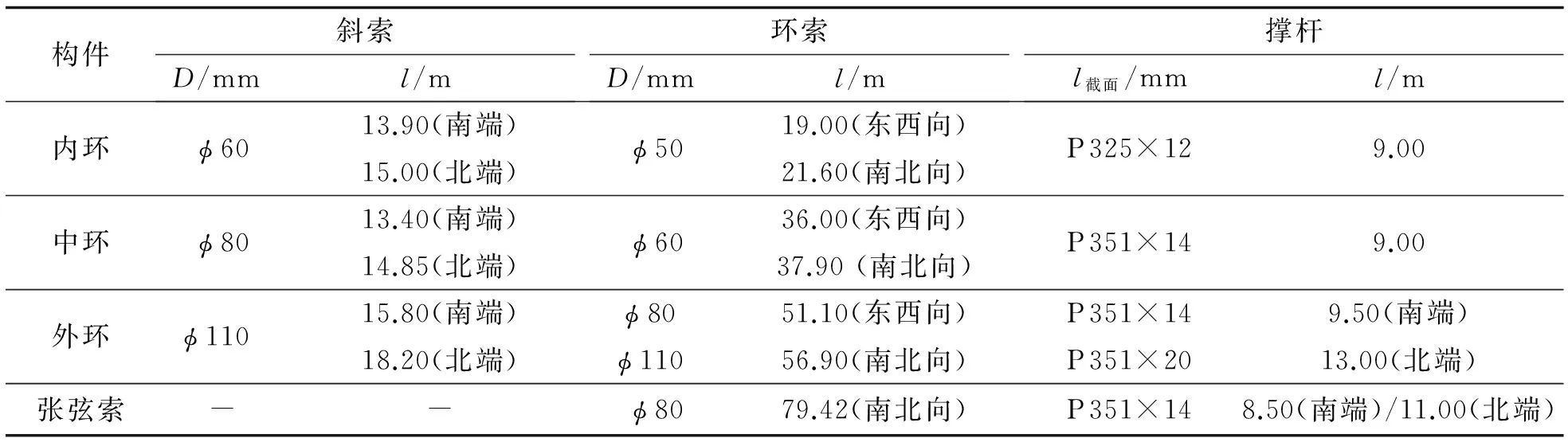
表1 拉索及撑杆参数Tab.1 Parameters of the cables and braces

2 数值模型建立及拉索张拉模拟

为精细模拟拉索张拉过程，实现多重四边环索-张弦结构的拉索张拉全过程仿真分析，并研究张拉过程中各索力及关键节点位移的变化规律，采用通用有限元软件SAP2000，建立整体钢结构屋盖的三维有限元计算模型，如图1所示.

在数值模型中，四边环索-张弦梁结构的网架为箱型截面，采用Frame单元模拟，钢材弹性模量E=206 GPa，体密度取7.85×103kg·m-3；预应力拉索采用Cable单元进行模拟，拉索弹性模量E=195 GPa，抗拉强度取1.67 GPa.撑杆单元采用Link单元模拟，从而保证在张拉过程中，撑杆上下两端可以自由转动.马道为该网架结构中的附属结构，在模型中仅考虑马道的自重(1.5 kN·m-1).网格梁最外层的环梁与劲性钢管柱耦合6个方向自由度，以模拟实际工程中固接连接.

索力张拉过程采用SAP2000中非线性阶段施工进行模拟，根据实际索力张拉顺序，把每一步索力张拉施工定义为一个施工阶段.其中，索力张拉过程采用降温法实现.即，根据式(1)算出每一步张拉索力所对应的温差，并在数值模型的对应工况施加温度荷载，以实现索力张拉过程.索力-温度换算公式如下：

式中：P为索力;α为材料的线膨胀系数;E为索的弹性模量;A为索的截面面积.

3 四边环索-张弦结构张拉方案初选

本研究背景屋盖四边环索结构的预应力通过张拉四边斜索张拉实现；而两边的张弦梁结构则采用单边张拉方式.因此，背景屋盖至少有14根拉索(斜索和张弦索)需要进行索力张拉施工.为了保证张拉过程中屋盖受力的渐近性和施工安全性，复杂弦支结构的一般是采用拉索分批张拉方式[7].因此，需要仔细研究不同的分批张拉顺序对四边环索-张弦结构受力和变形的影响规律.对于多重环索结构，内环斜索间的网格梁面积较小，如果先张拉内环斜索，容易引起网格梁的局部受力过大.对于多重环索，通常采取先外环斜索，后内环斜索的张拉顺序[8]，因此，根据本屋盖的结构特点，比较了两种不同顺序张拉方案.

张拉方案1：先张拉多重环索，再张拉张弦索，即：外环斜索—中环斜索—内环斜索—张弦梁拉索.

张拉方案2：先张拉张弦索，再张拉多重环索，即：张弦梁拉索—外环斜索—中环斜索—内环斜索；

文[4]针对环形预应力张弦梁屋盖的研究结果表明：适当的分阶段循环张拉不仅有利于拉索本身的受力，而且对结构其它部分的受力与变形也颇为有利，可有效地避免超应力构件的出现，保证施工阶段结构的可靠度.但是，过多的循环阶段会使得张拉效率低，施工工作量大大增加.综合相关工程施工经验及文献成果[9]，此多重环索-张弦梁屋盖结构分2级进行索力张拉，即：第1级张拉至张拉索力的50%，第2级张拉至100%.每级施工时，同时张拉环索的4根斜索或对称2根张弦索.

由于设计力为假设结构一次成型后施加结构自重和荷载得到的.而实际上结构的不同杆件是分阶段施工、安装和拼接起来的.施工顺序不同，结构杆件参与受力的顺序和程度也不同.因此，本研究首先采用逆向分析法[10]，即倒拆法，来模拟拉索张拉的全过程，计算每一个张拉阶段的张拉索力.针对前文提出的2 种索力张拉方案，本研究得到每个张拉步的设计张拉索力，如表2所示.

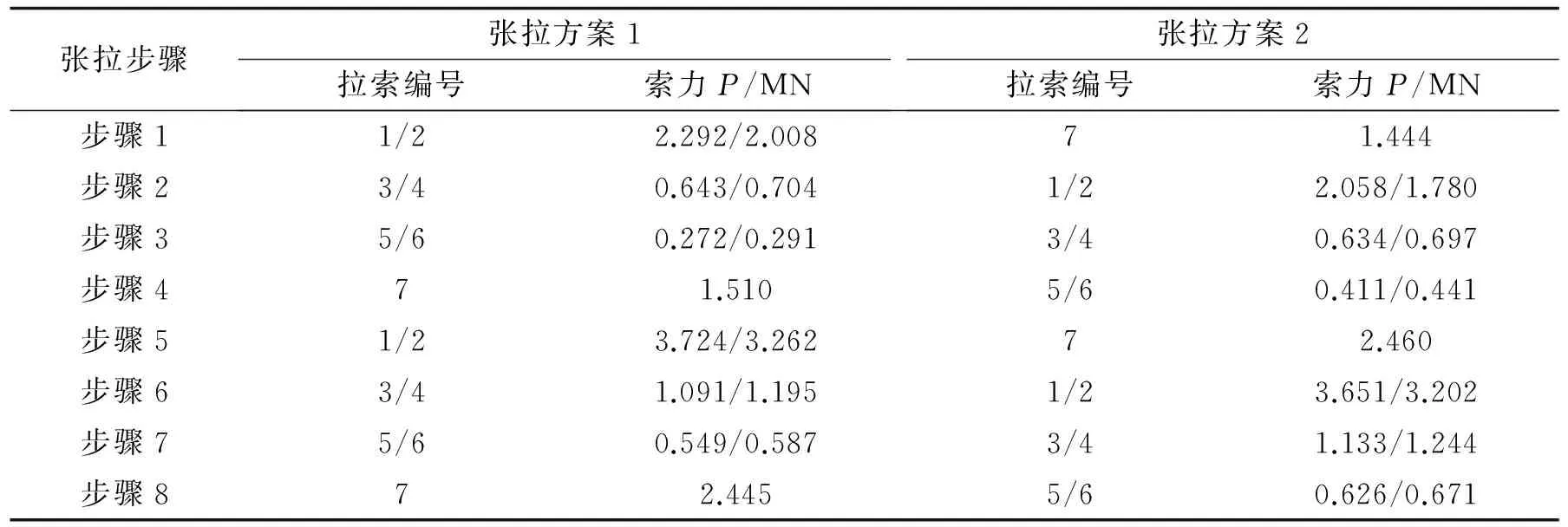
表2 各级张拉索力值Tab.2 Cable forces for each tensioning steps

注：拉索编号请参见图2(a)

4 张拉方案对比分析

基于SAP2000建立三维数值分析模型，采用降温法模拟斜索和张弦索的逐步张拉过程，得到不同索力张拉方案下屋盖结构的受力和变形规律.

4.1 屋盖结构变形

图3、图4分别为方案1和方案2中各阶段张拉施工过程中的屋盖结构竖向变形云图.文[6]对多重环索结构的研究表明，屋盖结构的竖向位移对于空间张弦结构的施工控制起到关键作用.因此，本研究进行方案比选时，以屋盖结构的竖向变形值作为重要参数之一.

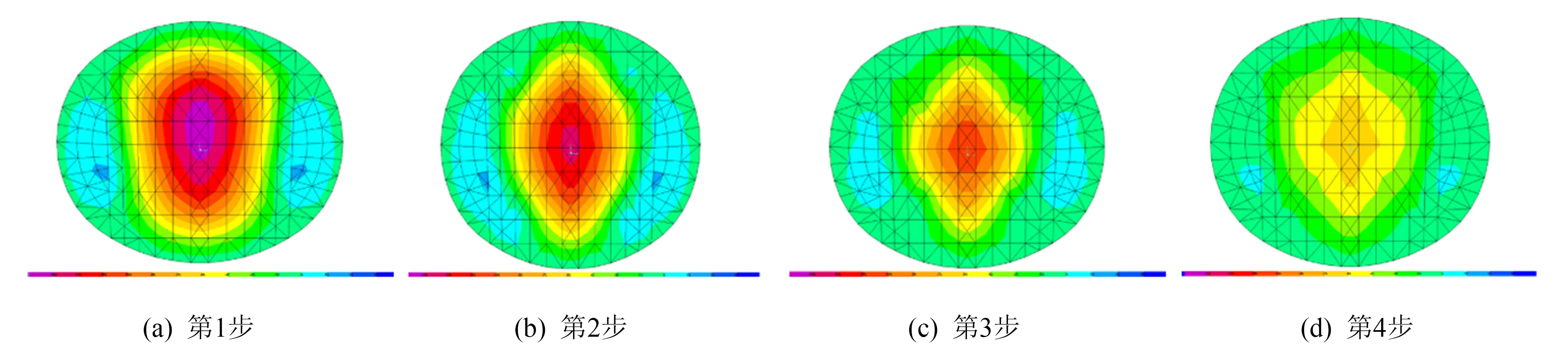
图4 屋盖竖向位移云图(方案2)Fig.4 Vertical displacements nephogram of roof (case 2)

由图4可以看出，方案2由于首先张拉张弦梁拉索，造成张弦梁撑杆附近的局部网架出现较大的向上变形；同时，在重力作用下屋盖跨中仍然有较大的竖向变形，因此，屋盖两侧与跨中正负位移值相差较大，屋盖变形明显.在应力云图中可看出有一椭圆形深色区域，表明此处变形较大.相反，方案1(图3)先张拉各级环索，屋盖受力区域大，整体屋盖变形较均匀，表现为变形云图的分布形状更为饱满.但是，随着张拉的进行，两方案的位移云图趋于相同.第5步～第8步为第2级施工，与第1级(第1步～第4步)张拉顺序相同，屋盖的变形规律也与第1级相似.2级张拉结束后，两种方案下的最终屋盖变形云图分布规律基本相同，与设计变形状态均吻合较好，如图4所示.总体来说，方案1的各级张拉过程中屋盖结构的竖向变形云图更加饱满，变形分布较为均匀.

为进一步了解不同张拉方案下屋盖最大位移值的变化规律，图5列出张拉过程中两种方案每一步的最大竖向变形值与最大上拱值.由该图可以看出，在不同的张拉步骤下，方案2的每一步中最大下挠值与最大上拱值均大于方案1.方案2的第一步张拉结束后，最大下挠值出现在屋盖中部，达到162 mm，较方案1增大约51%(107 mm)，与规范中最大挠度限值(跨长L/50=213 mm)十分接近.同时，在张弦梁撑杆附近出现屋盖上挠，第5步张拉结束后，方案2中屋盖最大上挠变形达45 mm，较方案1增大100%(27 mm).总体来说，方案1采用先张拉环索的方案，屋盖受力区域大，整体屋盖变形较均匀，张拉过程中未出现局部变形过大的问题；相反，方案2采用先张拉两侧张弦梁，较大的应力集中于张弦索周围，导致屋盖局部变形突出；而且，由于两侧张弦梁相距较远，造成屋盖局部变形突变大.综上所述，虽然两种张拉方案结束后，两种方案的屋盖竖向位移相差不大；但是，在施工过程中，方案1的屋盖竖向位移绝对值及屋盖自身变形量均小于方案2.

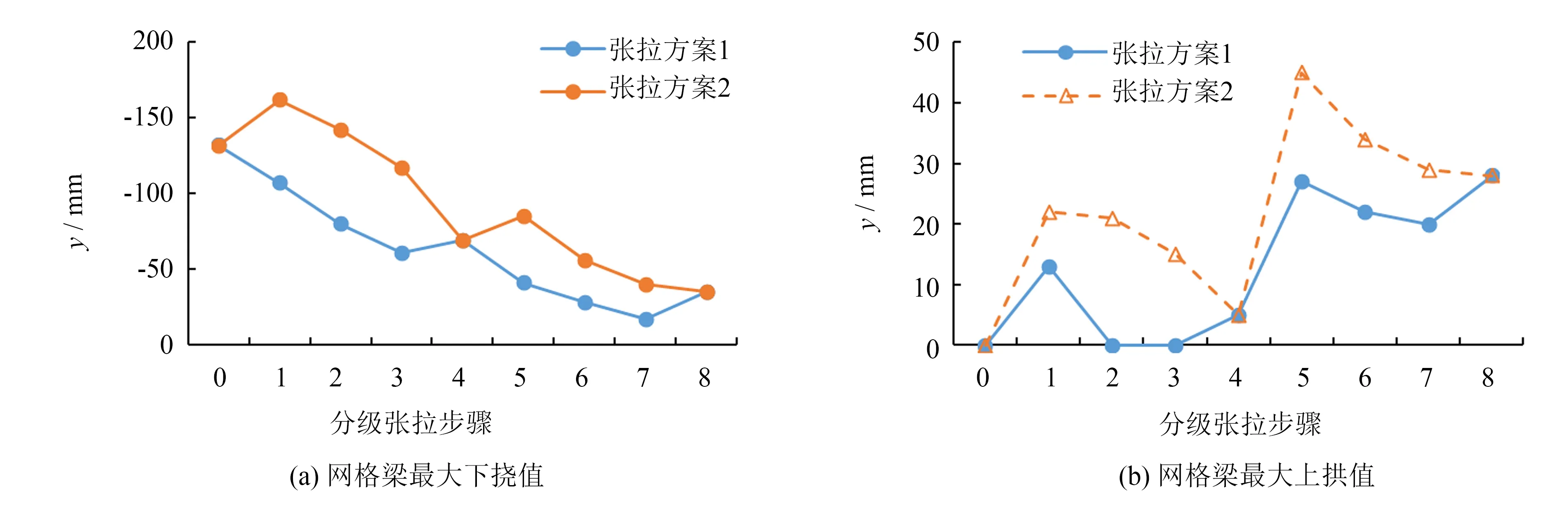
图5 网格梁竖向变形图Fig.5 Vertical displacements of grid beams

4.2 拉索及撑杆受力

图6为张弦梁索力和撑杆的轴力动态变化图.从图中可以看出，两种张拉方法最后得到的张弦索最大预应力基本相同，约2.036 MN.随着外环斜索的张拉，张弦索产生一定程度的索力损失，最大降幅度约为11%；但是随着中环斜索和内环斜索的张拉，张弦梁的索力回升至刚张拉完的应力水平.总体来说，在预应力张拉过程中，张弦索的应力水平为拉索极限拉力fyk的0.26～0.29倍.

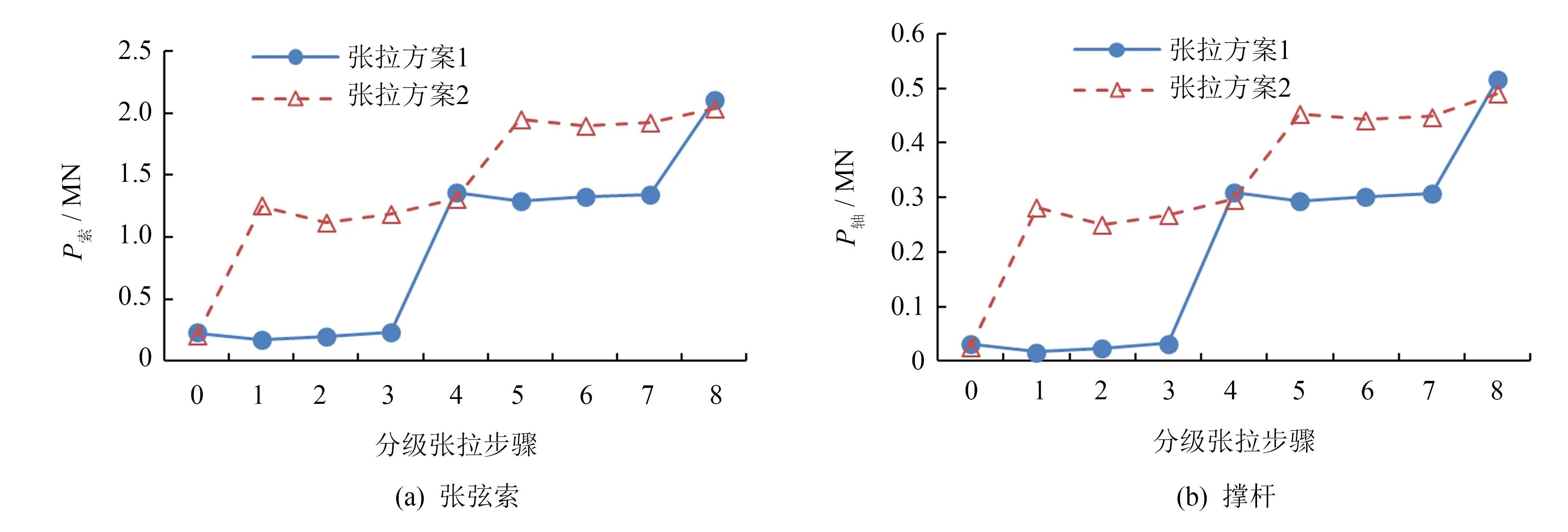
图6 张弦梁中构件轴力变化图Fig.6 Axial forces of beam-string structures

三重四边环索结构中，外环索的拉索跨度最长，拉索索力也最大.图7列出了外环索结构的斜索、环索和撑杆轴力在各张拉阶段的变化图.从图7(a)可以看出，两种张拉方案计算得到的四边形外环斜索最大预应力基本相同，约3.579 MN.随着中环及内环斜索的张拉，外环斜索及环索内力有所增加，增幅约为3%～7%；张弦结构拉索张拉后，外环斜索、环索内力略有下降，降幅在3%左右.由于斜索、撑杆和环索在每个撑杆节点为空间受力平衡体系.因此，在张拉过程中，环索和撑杆的内力变化规律与斜索大致相同，如图7(b)、(c)所示.张拉过程结束后，方案1 中各索最大拉力略大于方案2(3%左右)，其中外环斜索最大拉力约3.771 MN，环索内最大拉力约2.762 MN，竖向撑杆的最大轴压力为0.954 MN.但是，张拉过程中外环索各构件的应力水平都较低，其中斜索的预应力水平基本在(0.20～0.23)fyk之间，环索的预应力水平基本在(0.14～0.22)fyk之间.因此，在总体应力水平都较低的情况下，两种张拉方案对外环索的受力影响非常小.

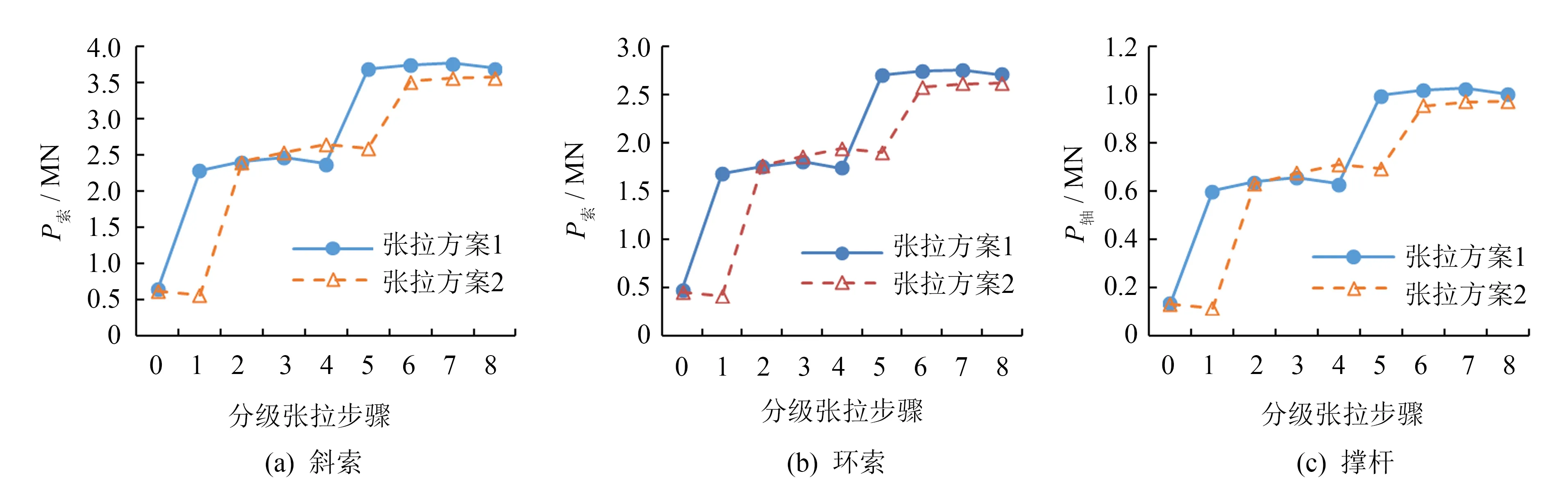
图7 外环各构件受力变化图Fig.7 Axial forces of outer-square loops

图8为中环各构件的内力变化图.当中环斜索还未张拉预紧时，中环体系还未成形，其中各构件未能与整体屋盖结构的受力重分布.因此，其它环索或张弦索的张拉对中环斜索中各构件的内力没有影响，如图8所示，前2个张拉阶段(方案2)中应力水平均未改变.但是，当中环斜索初张拉完后，与钢网格结构形成空间受力体系，其它拉索的张拉均会对中环各索的内力产生影响.当张弦索和外环斜索张拉时，均会使得中环索力增大，增幅约为2%～11%.在预应力张拉过程中，中环斜索的预应力水平基本在(0.13～0.15)fyk之间，环索的预应力水平基本在(0.12～0.18)fyk之间.

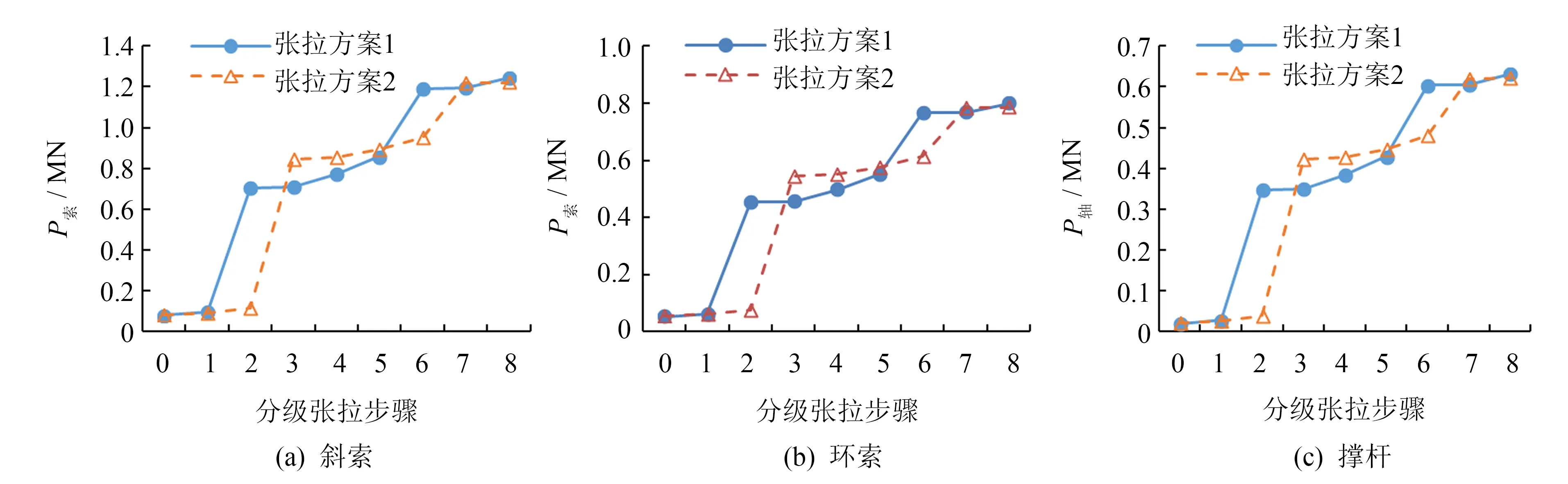
图8 中环各构件受力变化图Fig.8 Axial forces of middle-square loops

图9为内环各构件内力变化图.当内环斜索1级张拉参与屋盖结构受力后，其它环索或张弦索的张拉均会显著增大内环索的应力水平，应力增大幅度为1%～39%.其中，内环的斜索和环索随着张拉过程的进行，索力逐步增大.张拉方案1中，其内力增大更近似于多级逐步预紧拉力；而在张拉方案2中，环索索力增长则更集中，其应力增大主要发生于内环斜索的两级张拉施工阶段.整个预应力张拉过程中，内环斜索的预应力水平基本在(0.13～0.14)fyk之间，环索的预应力水平基本在(0.10～0.14)fyk之间.

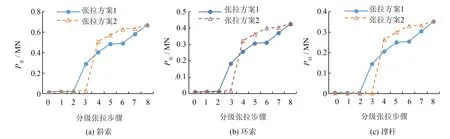
图9 内环各构件受力变化图Fig.9 Axial forces of inner-square loops

4.3 网格梁内力

斜索或张弦索的水平分力会使网格梁产生较大的轴力，同时，竖向撑杆的作用会引起网格梁结构的平面内弯矩.图10为张拉方案1结束后，网格梁的轴力和弯矩分布图.网格梁最大轴力发生在张弦索相交的方形钢管，其值为2.242 MN；网格梁最大弯矩值发生在外环撑杆交点处，网格梁最大弯矩约为931 MN·m.

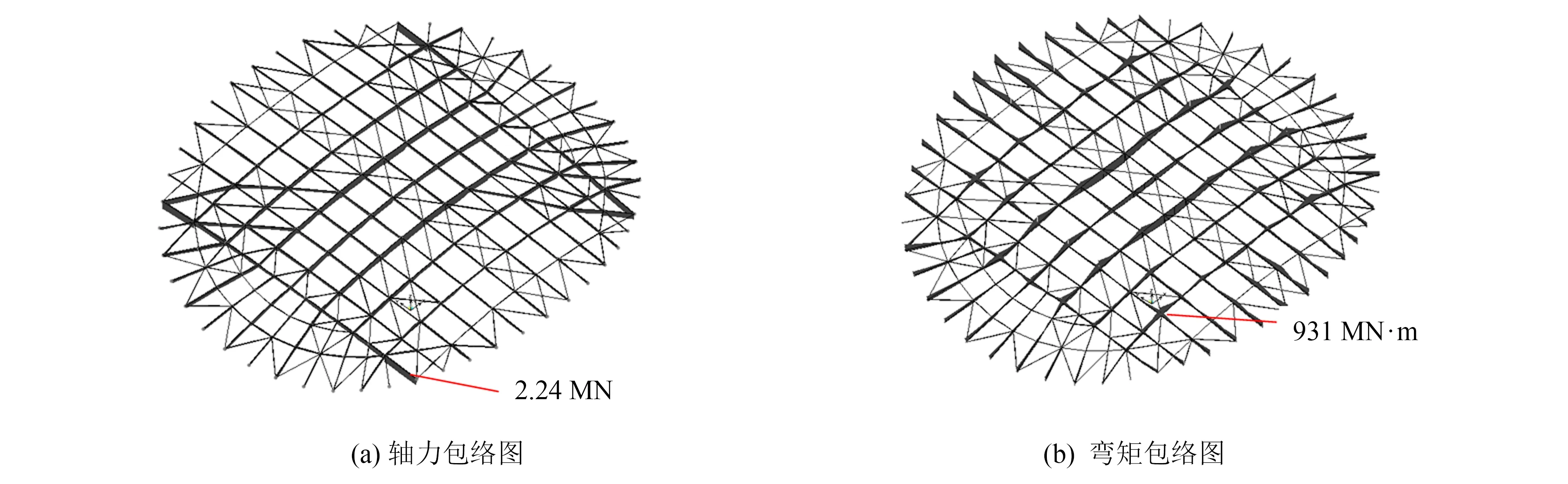
图10 网格梁内力分布图(方案1)Fig.10 Internal forces of grid beams (case 1)

图11分别为网格梁最大轴力和最大弯矩变化曲线.由图可以看出，不管采用何种张拉顺序，杆件最大轴力均随着张拉施工的开展而增长.从图 11(a)还可以看出，网格梁轴力的较大变化均发生在张弦索张拉工况中，这是因为网格梁的最大轴力发生在张弦索交点处，所以此构件内力受张弦索张拉施工的影响较大.

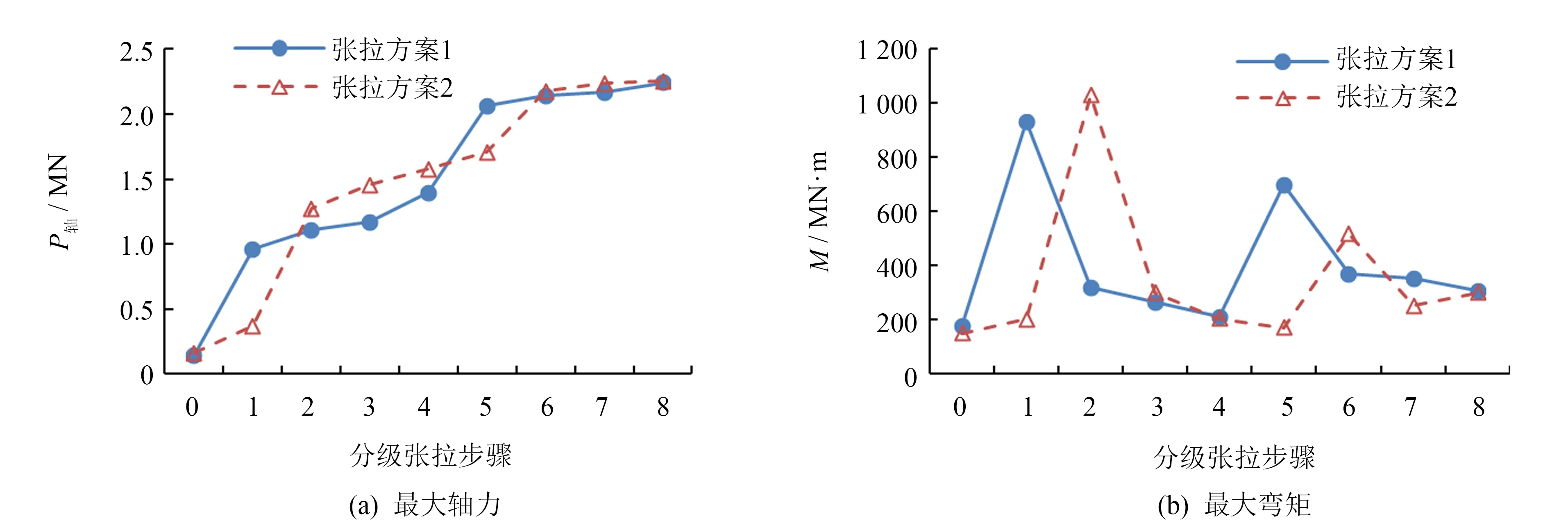
图11 网格梁最大内力变化图Fig.11 The maximum internal forces of gird beams

图 11(b)则表明网格梁最大弯矩并非随着索力张拉施工而持续增长，而是在外索斜索张拉时，网格梁最大面内弯矩达到峰值，这是因为最大弯矩发生于外环撑杆处，直接受撑杆的竖向作用力.因此，外索斜索张拉时，网格梁产生较大的面内弯矩.而且，当采用方案2 中网格梁最大弯矩为1.029 GN·m，较方案1增大10%(931 MN·m).由于网格梁的载面尺寸较大，其预应力水平基本在(0.10～0.20)fyk之间.因此，总体来说，不同的拉索施工顺序对于网格梁内力影响不大.

5 结语

1)两种张拉方案结束所得的屋盖竖向位移比较接近，但是，在索力张拉过程中，方案1中屋盖竖向位移较小，且屋盖自身变形更加均匀.

2)对斜索、环索、张弦索及撑杆的内力响应分析表明，各拉索张拉对环索结构和张弦结构内力变化影响较大；虽然不同的张拉顺序均能得到设计成形索力.但是，张拉过程中各索力的变化规律相差较大.总体来说，采用方案1 的张拉顺序时，屋盖结构中各构件内力变化较方案2更均匀.

3)不管采用何种张拉顺序，环索及张弦索最大轴力均随着张拉施工而持续增长；但是，网格梁最大弯矩则有增有减，其中，方案2中最大弯矩较方案1增大约10%.但是，施工完成后，网格梁的受力状态相差不大.

综上所述，考虑到张拉施工过程中屋盖结构变形和内力更合理，建议采用张拉方案1，即“外环索-中环斜索-内环斜索-张弦索”的张拉顺序.

[1] 陈志华,刘红波,王小盾,等.弦支穹顶结构研究综述[J].建筑结构学报,2010,31(增刊1):210-215.

[2] 张伟,张文耀,杨伟,等.海峡奥体中心体育馆钢结构监测系统研究[J].福建建筑，2015,205(7):21-23.

[3] 陈志华.弦支穹顶结构[M].北京：科学出版社，2010.

[4] 石开荣,郭正兴,罗斌.环形辐射状预应力张弦梁钢屋盖张拉优化[J].东南大学学报(自然科学版),2015,35(增刊1):55-60.

[5] 王哲,王小盾,陈志华,等.向心关节索杆体系弦支穹顶张拉模拟分析[J].建筑结构学报,2014,35(11):102-107.

[6] 林威.多重环索预应力空间张弦梁受力特性研究[D].福州:福州大学,2015.

[7] 刘红波,陈志华,牛犇.弦支穹顶结构施工过程数值模拟及施工监测[J].建筑结构学报,2012,33(12):79-84.

[8] 郭正兴,汤荣广,梁存之.预应力索-拱钢屋盖群索张拉优化研究[J].施工技术,2002,31(7):7-9.

[9] 王化杰,范峰,钱宏亮,等.巨型网格弦支穹顶预应力施工模拟分析与断索研究[J].建筑结构学报,2010,31(增刊1):247-253.

[10] 赵平,孙善星,周文胜.基于ANSYS的索穹顶施工过程逆向模拟分析[J].工业建筑,2013,43(4):127-130.

(责任编辑：沈芸)

Comparativeanalysis on cable tensioning scheme of multiple square loops-string dome

ZHANG Chao1,YU Li1,XU Li1,LIN Wei2

(1.College of Civil Engineering,Fuzhou University,Fuzhou,Fujian 350116,China;2.Fujian Communications Planning & Design Institute,Fuzhou,Fujian 350002,China)

Multiple square loops-string dome (MSLSD)has quite various mechanics under different cable tensioning sequences.In order to optimize the cable tensioning sequences,the first MSLSD project that is Fuzhou Olympics Gymnasium was taken as research background.And the investigations are carried on to proposed two different cables tensioning schemes.Based on the 3D finite-element model,the internal forces and deformations of the MSLSD under different cables tensioning schemes are discussed.The process of cable tensions is simulated by cooling method.The analysis results shows that the roof internal forces and deformation during cable tensioning stage for two schemes are quite different,although the final results are nearly the same.During the tensioning process,roof deformation and internal force of grillage girder are obviously less for the 1sttensioning schemes.Therefore,considering the safety during construction,the 1sttensioning schemes are recommended,whose sequence is “external cables square loop-middle cables square loop-internal cables square loop-cables of string beam”.

multiple square loops (MSL); beam string; dome; cables tensioning

10.7631/issn.1000-2243.2017.02.0151

1000-2243(2017)02-0151-08

2015-10-11

张超(1985-)，副研究员，硕士生导师，主要从事大跨结构防震减灾研究,zhangchao1985@fzu.edu.cn

教育部博士点基金资助项目(2013351420006)；福建省自然科学基金资助项目(2013J05072)；福建省教育厅科技资助项目( JK2014005)

TU356

A