中俄高中几何教科书比较研究

徐乃楠，马晓艳(吉林师范大学数学学院，吉林四平 136000)

中俄高中几何教科书比较研究

徐乃楠，马晓艳
(吉林师范大学数学学院，吉林四平 136000)

俄罗斯高中数学课程教科书在世界范围内广受推崇，其中代数与数学分析初步和几何分科编写，几何教科书重视数学公理化体系，具有较高的知识难度，对我国当前高中数学课程标准修订和实验教科书编写具有重要的借鉴意义。

俄罗斯；几何；高中教科书

俄罗斯联邦高中数学教育标准对高中学生的数学学习要求分为基础水平(БАЗОВЫЙ УРОВЕНЬ)和专业水平(ПРОФИЛЬНЫЙ УРОВЕНЬ)两个层次[1]，教育标准下有示范性教学大纲[2]，在教育标准和示范性大纲指导下还有著名数学家编写的各种教科书。本文针对高中学段数学教科书的核心内容——几何模块，选取我国《普通高中课程标准实验教科书》(人教A版)和俄罗斯卡列宁和捷列圣编写的《几何》教科书,进行文本比较研究。

1 俄罗斯《几何》教材简介

捷列圣·德米特里·亚历山德洛维奇(Терёшин Дмитрий Александрович，1967- )，是莫斯科物理技术学院(Московский физико технический институт)数学系的副教授，2010年曾获得俄罗斯联邦教育奖，出版过13本立体几何和数学奥林匹克方面的书籍。

莫斯科物理技术学院被誉为俄罗斯的MIT，一直积极参与数学教育研究和数学教科书、奥林匹克数学参考书编写，尼科利斯基院士曾在那里工作过。卡利宁·亚历山大·尤里耶维奇(Калинин Александр Юрьевич)是捷列圣的学生，1996年移居美国，现工作在亚马逊公司。二人合写的《几何》(10-11年级合订本)教科书由莫斯科继续数学教育中心(Московский центр непрерывного математического образования)出版。该书是俄罗斯联邦国家教育和科学部批准使用的高中数学教科书，2011年莫斯科继续数学教育中心出版了新修订补充本[3]。俄罗斯的教科书有的专门用于基础水平的学生学习使用的，有的是专门用于专业水平的学生使用，有的是同时可供基础和专业水平的学生使用[4]。该书可以提供给10-11年级学生,用于专业水平的学习使用。

该书是合订本，但在具体编写中分为10、11两个年级，主体知识内容共有13个章节，具体章、节、内容与我国高中几何模块比较情况如表1所示。其中带有星号的知识点例如欧拉定理、空间三角形相等定理和相似定理、空间中的相似变换和移动分类、旋转体和多面体的非标准组合、圆锥曲线，以及整个第九章问题解决的知识等内容，教科书扉页注释中指出是“高于正常难度的内容”。

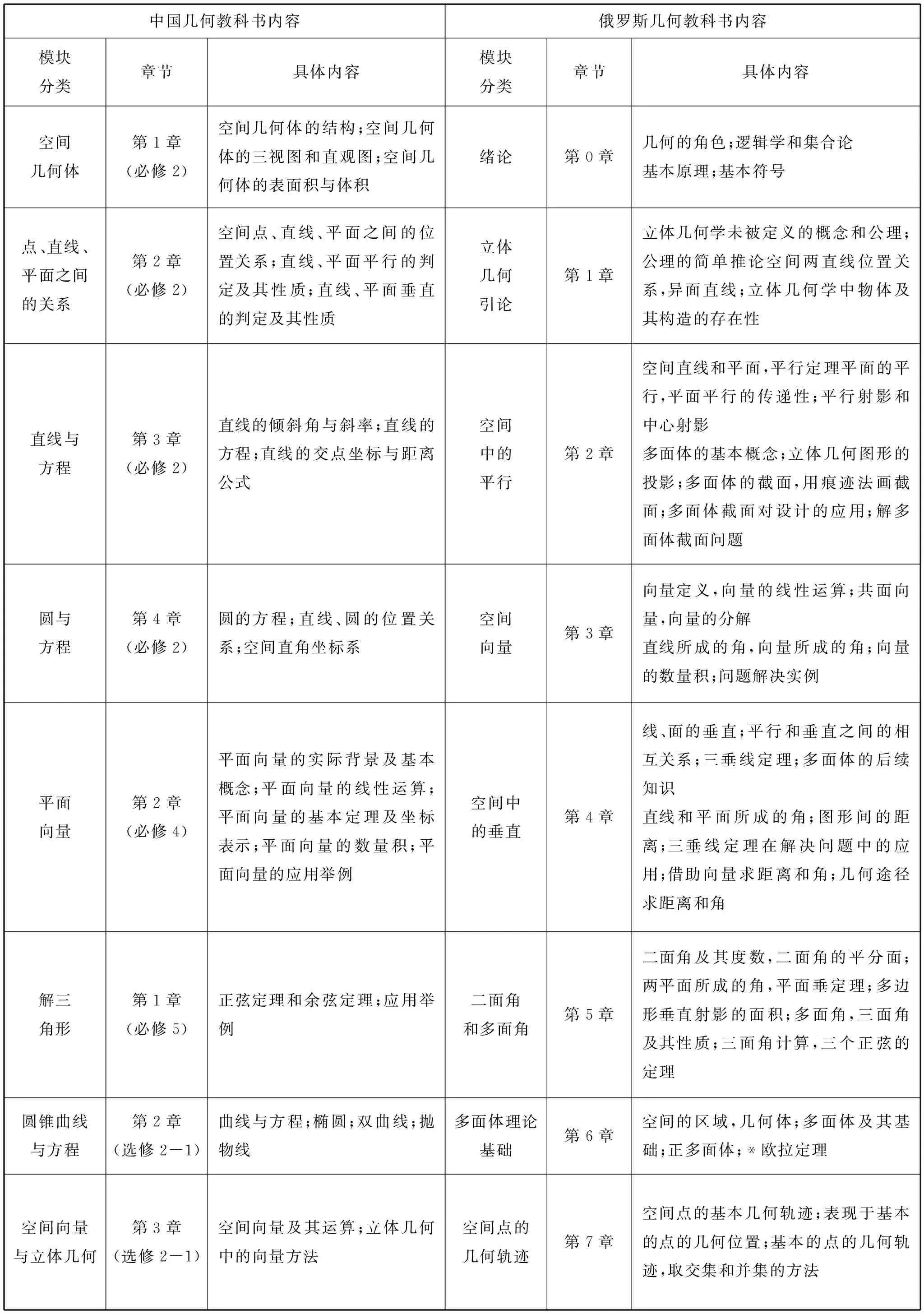
表1 中俄高中几何教科书主要内容

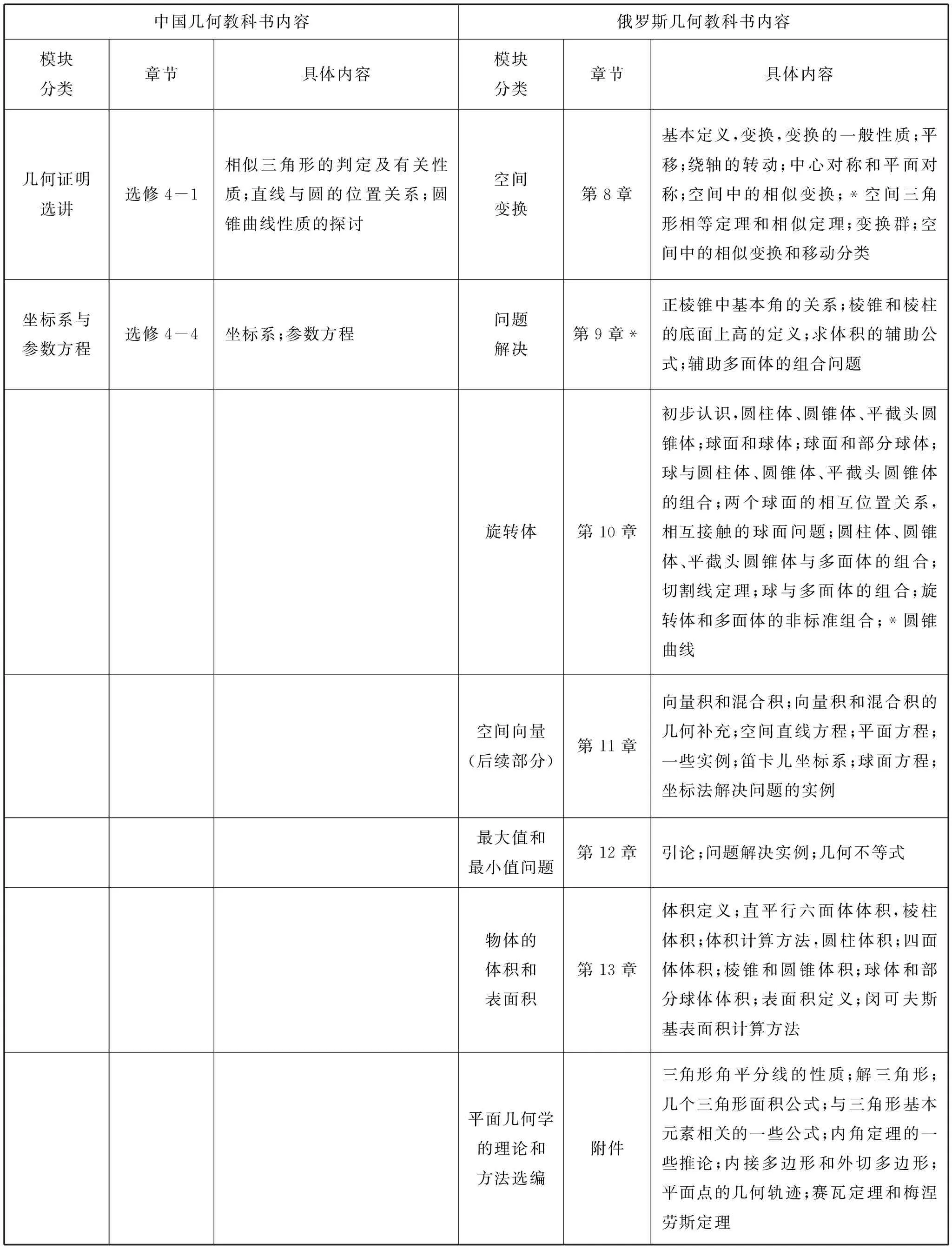
中国几何教科书内容俄罗斯几何教科书内容模块分类章节具体内容模块分类章节具体内容几何证明选讲选修4-1相似三角形的判定及有关性质;直线与圆的位置关系;圆锥曲线性质的探讨空间变换第8章基本定义,变换,变换的一般性质;平移;绕轴的转动;中心对称和平面对称;空间中的相似变换;*空间三角形相等定理和相似定理;变换群;空间中的相似变换和移动分类坐标系与参数方程选修4-4坐标系;参数方程问题解决第9章*正棱锥中基本角的关系;棱锥和棱柱的底面上高的定义;求体积的辅助公式;辅助多面体的组合问题旋转体第10章初步认识,圆柱体、圆锥体、平截头圆锥体;球面和球体;球面和部分球体;球与圆柱体、圆锥体、平截头圆锥体的组合;两个球面的相互位置关系,相互接触的球面问题;圆柱体、圆锥体、平截头圆锥体与多面体的组合;切割线定理;球与多面体的组合;旋转体和多面体的非标准组合;*圆锥曲线空间向量(后续部分)第11章向量积和混合积;向量积和混合积的几何补充;空间直线方程;平面方程;一些实例;笛卡儿坐标系;球面方程;坐标法解决问题的实例最大值和最小值问题第12章引论;问题解决实例;几何不等式物体的体积和表面积第13章体积定义;直平行六面体体积,棱柱体积;体积计算方法,圆柱体积;四面体体积;棱锥和圆锥体积;球体和部分球体体积;表面积定义;闵可夫斯基表面积计算方法平面几何学的理论和方法选编附件三角形角平分线的性质;解三角形;几个三角形面积公式;与三角形基本元素相关的一些公式;内角定理的一些推论;内接多边形和外切多边形;平面点的几何轨迹;赛瓦定理和梅涅劳斯定理

从整体上看，中国教科书的每册内容都是围绕一个主体，每册书由几章组成，每章又由几小节组成，知识划分比较细致。中国人教A版教科书几何部分分为必修和选修，其中必修部分共6章，大部分集中在必修2的内容中，选修部分共4章,包括立体几何、空间向量以及圆锥曲线内容。俄罗斯教科书每册包含了不一样的主题，相同主题的内容化为一章，因此从章节上看，相同知识点所划分的章数比中国教科书多，知识形式比较全面。

2 中俄几何知识结构比较分析

2.1 两国几何教科书内容不同

从整体内容上看，两国教科书中知识量差异较大，中国教科书所含内容在俄罗斯教科书中都能找到，但是俄罗斯教科书中的一些知识在中国教科书中没有体现，如“多面体最优化、梅涅劳斯定理、赛瓦定理、空间求面坐标系、定向曲面和麦比乌斯带、星状多面体、凸几何分析、变换群”等，都是我们数学专业课中才能学到的内容。从细节上看，俄罗斯教科书中多数知识点设置体现在习题中，中国教科书的知识点都设置在正文中，如：对于面面垂直的性质定理,在俄罗斯教科书中是作为习题结论给出的。教科书中很多知识的学习都是通过学生探究交流、动手探究实现的。

2.2 两国几何教科书知识安排顺序不同

俄罗斯教科书的内容组织建立在公理体系基础上，第一章内容把几何公理作为引论,在全书知识内容之前做好铺垫，这对数学思维的发展有良好的影响，有利于学生理解数学理论的抽象本质和意义。然后，以公理为基础来研究点、直线、平面之间的性质及其位置关系，进而研究以它们为元素组成的棱柱、棱锥、球等空间几何体。我国高中教科书先把立体几何作为开头，在“空间几何体结构”内容中展示了大量几何体实物、模型、图片等，学生可以感受空间几何体的整体结构，深入认识点、直线、平面之间的位置关系。中国教科书先学习多面体和旋转体的概念及体积和表面积，而俄罗斯教科书将其放在第二章、第六章和第十章,对多面体和旋转体进行分类讲授。对于空间直线与平面平行与垂直的内容，中国教科书将其放在一章中学习，其本意是把二者归为空间中直线与平面的特殊位置关系这一类内容，而俄罗斯教科书把这一内容分为两章，对平行与垂直分类讨论，并且这两章并不连续，中间是向量知识，对于垂直问题可直接用向量法解决。

2.3 两种教材习题设置不同

中国教科书在每节结束后会设置一些习题，使学生巩固所学内容。按难度分为A、B两组，其中B组难度稍大，这样设置有利于学生复习。俄罗斯教科书在每个单元教学内容完成之后都有一个小小的习题系统，并且由简单到复杂层层递进，对教师和学生都有较高的要求。

3 对我国高中几何教科书编写的启示

3.1 处理好高中几何教科书难度

俄罗斯高中《几何》教科书中数学知识内容涉及向量的数量积、混合积及其几何意义，梅捏劳斯定理和赛瓦定理，多面体最优化问题，空间球面坐标系，定向曲面与麦比乌斯带，星状多面体，凸几何分析问题，变换群等内容，有的已经超出教育标准的要求[5]。我国高中数学课程对一些难度较高的数学知识不是没有考虑，只是全都设计在选修课程当中，编有独立的选修教科书，内容与必修课程的联系不够密切。选修系列涉及的几何内容有“对称与群、欧拉公式与闭曲面分类、球面上的几何、三等分角与数域扩充”等内容，有的是俄罗斯高中数学课程中没有的。但这些选修知识需要各个学校、教师根据情况单独开课，事实上很多学校老师也没为学生开设这些专题讲座，其原因主要是因为高考不考这些内容，很多一线高中教师对这些现代数学内容把握不好。俄罗斯高中教科书中难度较高的知识点，是在必修内容或后续部分呈现的，二者联系较为密切，有鲜明的接续性，我国高中教科书中的高难度知识点，需要学生进行更大范围的拓展性学习，对提高学生掌握必修内容的水平并不一定具有实质性作用。

3.2 处理好高中几何教科书的编写方式

俄罗斯高中《几何》教科书总体遵循直线顺序编排几何知识内容，但也存在小螺旋编排结构，例如，教科书第十年级的第三章“空间向量”主要讨论“向量的定义、运算和数量积”等内容，第十一年级的第十一章继续讨论“空间向量(后续部分)”，内容涉及“向量的混合积及几何意义，空间直线、平面、球面方程的向量表达”等问题。我国高中数学采用呈螺旋式上升方式编写的教科书，代数、几何和概率统计等内容混排，在一些知识点的螺旋编排衔接上需要我们进一步完善的。另外，俄罗斯几何教科书内容建立在公理体系基础上，第一章内容基本把几何公理作为引论,在全书知识点讲授前做好铺垫，几何公理化是俄罗斯几何教科书最显著的特征。教育家们的理由是“它对数学思维的发展给予良好的影响，有利于理解数学理论的抽象性的本质和意义，保证了有可能把理论应用到种种具体情况中去。”[6]虽然受到西方新数学运动影响的俄罗斯数学教育改革中公理化特点逐渐弱化，在初中阶段教科书中著名数学家沙雷金的直观几何影响很大，但俄罗斯大部分中小学几何教科书主要还是以几何公理化体系组织知识内容，同时综合向量和坐标几何等现代几何内容,而平面解析几何尤其是圆锥曲线内容基本上是选修的内容。因此，如何将直观和逻辑有效地结合起来值得我们思考，平面几何和空间几何的统一教学体系究竟应该包括哪些基本内容需要我们深入研究[7]。

3.3 处理好高中代数和几何课程分和问题

关于教科书的分科编写还是混合编写的问题，一直是我国高中数学课程中争论不休的问题。争论的双方都有论据、各执一词。提倡综合课程的认为利于学生综合数学素养的形成，数形结合有利于学生更好地进行数学学习。提倡分科课程的认为，不同教师负责不同科目有利于教师发挥自身优势，也有利于学生有指向性地学习不同数学知识。在这一点上俄罗斯小学(1～4年级)教材是综合课程，就叫《数学》，包括算数、代数初步和几何课程初步的内容，而初中5～6年级教材为《数学》，7～9年级则分为《代数》与《几何》两科，高中分为《代数与分析初步》和《几何》。高中数学课程改革不要仅仅做表面文章，更应关注课程内容，关注课程和教科书的知识内容。

[1]徐乃楠,孔凡哲.俄罗斯高中数学教育标准最新进展及启示[J].数学通报,2013(4):5-8.

[2]徐乃楠,孔凡哲,史宁中.俄罗斯高中数学示范性大纲最新进展研究[J].长春师范大学学报,2014(3):117-124.

[3]А. Ю. Калинин, Д. А. Терёшин. Геометрия[M].10-11 классов(профильный уровни), Москва: МЦНМО,2011.

[4]徐乃楠,孔凡哲,史宁中.俄罗斯高中数学教科书研究及启示[J].长春师范大学学报,2014(6):165-168.

[5]徐乃楠,孔凡哲,史宁中.俄罗斯高中数学教育标准、示范性大纲和教科书的最新变化特征及启示[J].全球教育展望,2015(1):100-109.

[6]A.A.斯托利亚尔.数学教育学[M].丁尔陛,等,译.北京:人民教育出版社,1984:169.

[7]徐乃楠.中俄高中数学教科书中的数学史研究[M].长春:东北师范大学出版社,2014:275.

Comparative Research on the Geometric Textbooks Between Russian and Chinese

XU Nai-nan,MA Xiao-yan

(College of Mathematics, Jilin Normal University, Siping Jilin 136000, China)

The Russian textbooks of senior high school mathematics curriculum is widely respected in the world, the geometry and algebra and mathematical analysis had division writing, Geometry textbook pays attention to mathematical axiomatic system, knowledge has a high difficulty, it is of great significance for the revision of the mathematical curriculum standards and textbooks of senior high school in China.

Russian；Geometry；Senior high school mathematical textbook

2017-01-02

国家社会科学基金2012年度教育学重点课题“中小学理科教材国际比较研究”(AHA120008)；吉林省教育科学“十二五”规划课题“俄罗斯数学课程改革最新进展研究”(GH14205)；吉林省教育厅“十三五”社会科学研究项目“中俄中小学数学课程比较研究”(吉教科文合字[2016]第176号)。

徐乃楠(1979- )，女，副教授，硕士生导师，博士，从事数学课程与教学论研究。

G423.07

A

2095-7602(2017)04-0112-05