讲评试卷预设专题,由表及里明辨模型
——以“a+k·b”线段最小值专题辅导为例
2017-04-24江苏苏州市吴江区笠泽实验初级中学张赞
☉江苏苏州市吴江区笠泽实验初级中学张赞
讲评试卷预设专题,由表及里明辨模型
——以“a+k·b”线段最小值专题辅导为例
☉江苏苏州市吴江区笠泽实验初级中学张赞
中考复习期间会有大量的模考题出现在备考师生面前,绝多数模考题的得来多是简单复制、拿来主义.最近复习过程中,我们在某份模考卷上选用了一道2016年中考原题,该题最后一小问与前面小问之间缺少关联,参加模考的学生几乎“全军覆没”,这促使我们深入思考应该如何应对这类难题的讲评.本文先介绍该题的思路突破,进而展示我们针对这一类型试题的专题辅导.
一、一道“拼凑式”压轴题及难点突破
考题:如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1,△AEN的周长为C2,若=,求m的値;
(3)如图2,在(2)的条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+E′B的最小值.
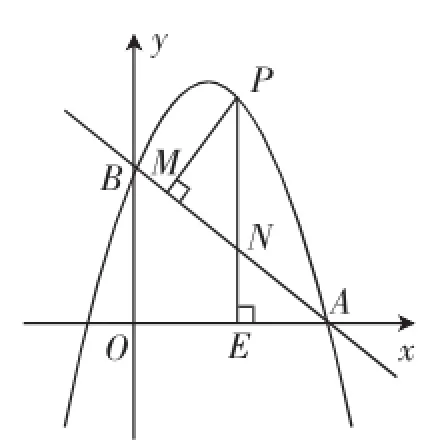
图1

图2
思路简述:前两问比较常规,限于篇幅,这里略去思路,直接给出答案(.1)a=-,直线AB的函数表达式为y=-x+3;(2)m的值为2.
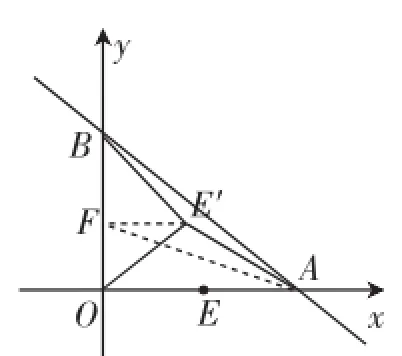
图3
(3)在上一问的条件下,容易确认点E(2,0),OE=2.由于这一小问与前面抛物线、动直线PE已无关,于是把无关线条删减之后,在图3中进一步构图
化为两个定点之间的距离,我们预设了如图4所示的PPT,辅导讲解.
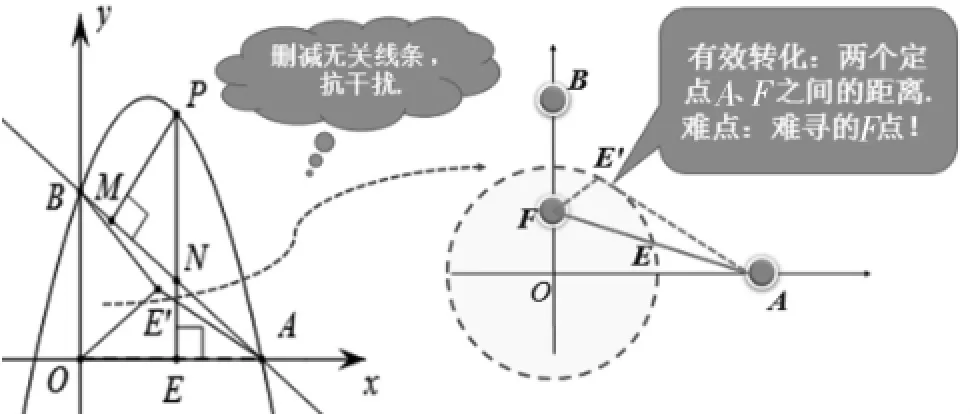
图4

解后反思:由于该题最后一问需要较高难度的构图,多数学生在没有接触过的情况下,在考场上没有顺利突破在情理之中,该题的构图背后有一个“高观点”知识的结构,这就是所谓“阿波罗尼斯圆”问题.(百度可知:阿波罗尼奥斯(Apollonius of Perga,约公元前262—190年),古希腊数学家,与欧几里得、阿基米德齐名)
由于形如“a+k·b”线段最小值问题在初中阶段不太常见,我们拟对该类专题进行辅导,作为这道考题的拓展式讲评,以下就是该专题的教学简案.
二、形如“a+k·b”线段最小值的专题辅导设计
因为复习讲评时间有限,本专题辅导仅关注k≠1的情形.
教学环节(一)“胡不归”问题.
例1(2016年徐州卷压轴题,有删减)如图5,在平面直角坐标系中,二次函数y=ax2+bx+c的图像经过点A(-1,0)、B(0,-)、C(2,0),其对称轴与x轴交于点D.
(1)求二次函数的表达式及其顶点坐标;

图5

图6
预设讲评:(1)二次函数的表达式为
(2)如图6,过P点作DE⊥AB于E点,由题意已知∠ABO=30°.
拓展讲评:可先介绍所谓的“胡不归”故事(限于篇幅这里不摘引),但告知学生故事真假需要存疑,我们只需要感受其中的数学智慧,并且“胡不归”问题的本质是光线在不同介质中的传播,早在17世纪世界业余数学家之王费马就曾对该问题有过深刻的思考,供有兴趣的学生课后链接学习.
教学环节(二)“阿氏圆”问题.
例2(2016年北京东城区中考一模,压轴题改编)如图7,△ABC中,∠BAC=90°,AB=AC=2,⊙A与BC边相切,点P为⊙A上一动点,连接PB、PC.试求PC+PB的最小值.

图7

图8
预设讲评:首先确认圆的半径为,在AB边上取点Q,构造△APQ∽△ABP,可将PB转化为PQ,再利用相似三角形对应比之比分析出AQ的长为1,从而确定Q点的位置,连接CQ交⊙A于P′,则此时PC+PB取得最小值.
预设小结:数学史话介绍(对古希腊数学家阿波罗尼斯作出简要介绍),并帮助学生总结“阿氏圆”问题一般解题步骤:如“PC+k·PD”最小值的构图(如图9~11)步骤如下:
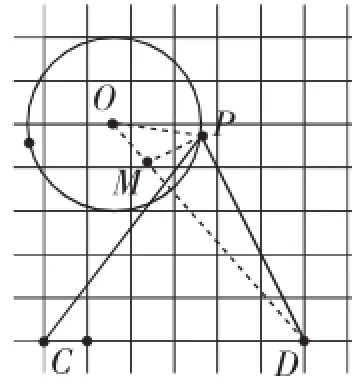
图9

图10
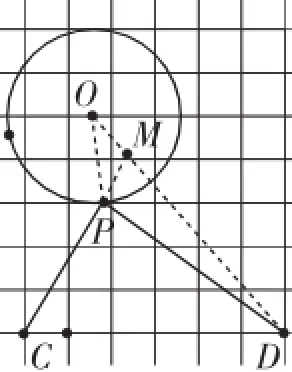
图11
第一步:连接动点与圆心O(将系数不为1的线段的两个端点分别与圆心相连接),则连接OP、OD;
第二步:计算出所连接的这两条线段OP、OD的长度;
第五步:连接CM,与圆O的交点即为点P.
教学环节(三)评讲“考题”.
重点讲评上面的“考题”第(3)问.
教学环节(四)同类训练.
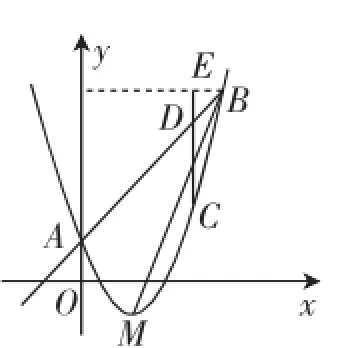
图12
训练题:(2016年重庆B卷,改编)如图12,顶点为M的抛物线y=x2-2x+1与直线y=kx+b(k≠0)交于A、B两点,点A的坐标为(0,1),点B在第一象限内.
(1)求直线AB和直线BM的解析式;
(2)点C为抛物线在第一象限上一点,且点C到x轴的距离是,在线段AB上找一点D(不与点A、B重合),求CD+BD的最小值.
设计意图:容易确定直线AB的解析式为y=x+1;直线BC的解析式为y=2x-5.进而构造等腰直角三角形BDE,将BD转化为DE,当C、D、E三点共线时,CD+BD取得最小值.
三、写在后面
经由上述专题辅导后,不少学生反映对这两类问题有较深的理解,特别是明辨了类似结构的最小值问题的不同模型.这对今后我们的中考专题复习也带来了更多的研发视角,这就是不仅可以是以往以开放题、探究题、动态题、图形变换题等形式化的分类辅导,而且可以从一些难题的突破策略或某类解题模型或问题深层结构的角度构造、研发中考专题,想来这应该是一个很有意义的研究方向,就让我们共同努力、丰富相关课例吧!
1.陈蓓蓓.例说几何定理教学的层次——由傅种孙先生数学教育思想说起[J].中学数学(下),2016(12).
2.罗增儒.数学的领悟[M].郑州:河南科学技术出版社,1997.
3.孟慧.几何综合题研究:从思路贯通到教学微设计[J].中学数学(下),2016(9).
