从试题、解题赏析走向“一题一课”教学——以2016年温州卷第23题为例

☉浙江乐清市大荆镇第一中学俞卫胜

从试题、解题赏析走向“一题一课”教学
——以2016年温州卷第23题为例

☉浙江乐清市大荆镇第一中学俞卫胜

近读《中学数学》2016年10月初中版，江苏省无锡市新区许燕老师针对2016年无锡卷第27题从考题与思路简述、一题一课教学微设计、教后反思这三个方面进行了思考，笔者深受启发.恰巧2017年1月在温州市初中数学初高衔接教研活动中，笔者就2016年温州卷第23题进行了一题一课教学，得到听课老师的一致好评.本文从考题、试题赏析与思路简述及该课的教学设计，给出教后反思，供研讨.

一、试题赏析与思路简述

考题：（2016年浙江温州，第

23题）如图1，抛物线y=x2-mx-3（m＞0）交y轴于点C，CA⊥y轴，交抛物线于点A，点B在抛物线上，且在第一象限内，BE⊥y轴，交y轴于点E，交AO的延长线于点D，BE=2AC.

（1）用含m的代数式表示BE的长.

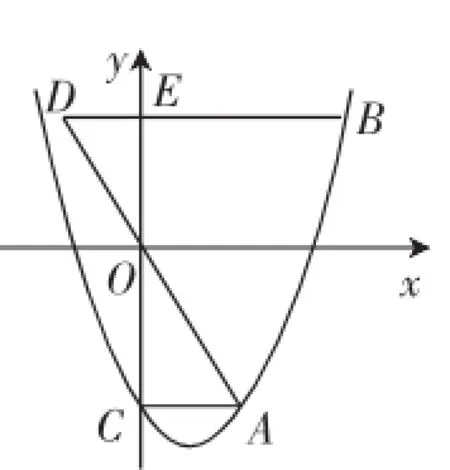
图1

（3）AG∥y轴，交OB于点F，交BD于点G.

①若△DOE与△BGF的面积相等，求m的值.

②连接AE，交OB于M，若△AMF与△BGF的面积相等，则m的值是________.

试题赏析：本题以动态的抛物线为背景，随着m的改变，牵一发而动全身，充分考查学生的转化能力，较好体现了数形结合的思想，同时渗透了动态中不变的量即点C始终不动.问题（1）的解法体现了抛物线的对称性，但若学生没有想到，仍然可以用“解析式求点”的方法求得点A的坐标，这样就兼顾了大部分学生，真正体现不同层次学生可以用不同的方法解决问题.对于问题（2），关键要熟练掌握点坐标与解析式之间的转换，进行由点求解析式和由解析式求点即两点定线，两线定点.综合考查二次函数、一次函数、全等三角形等知识点，方法多样，体现较好的区分度.问题（3）巧妙地将三角形面积与边长建立联系，层层递进，考查学生的转化能力，对学生的探究能力要求较高，在突出数学思想方法的理解与简单应用的同时，将数学基础知识、基本技能与能力的考查有机结合.

思路简述：

（1）因为BE=2AC，只要将AC用含m的代数式表示即可.由CA⊥y轴可得A、C的纵坐标相同，即把y=-3代入抛物线的表达式，可得x=0或x=m.所以AC=m，则BE=2AC= 2m.

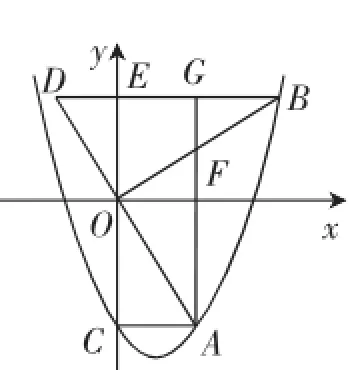
图2

（2）（几何法）当m=■3时，这个抛物线就确定下来了，只要求出点D的坐标就可以判断点D是否落在抛物线上.BE=2AC=2，把x= 2代入抛物线y=x2-x-3，得y=3，即OE=3.容易证明△AOC≌△DOE，即得D（-，3）.把x=-代入y=x2-■3x-3，得y=3，所以点D落在抛物线上.

（3）①因为∠ACE=∠CEG=∠EGA=90°，可得四边形ECAG是矩形，即EG=AC=BG.又FG∥OE，且EG=BG，所以EO=2FG.又因为·DE·EO=·GB·GF，则2DE=BG=

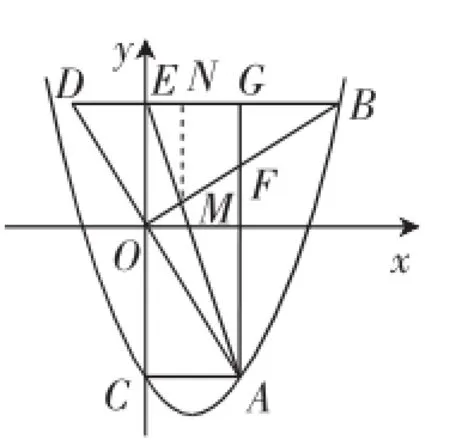
图3

②（转化法）过M作MN⊥BE交BE于点N，当S△BGF=S△AMF时，S△BGF+S四边形EMFG=S△AMF+S四边形EMFG，即S△BEM=S△AEG.又BE=2EG，所以对应高（2m2-3）］=m2.不难得到点N是EG的中点，可得BN=

另解：（解析法）由A（m，-3）、B（2m，2m2-3）、E（0， 2m2-3），得直线AE∶y=-2mx+2m2-3，直线OB∶y=则消去y，得解得，即点M的横坐标为.因为△AMF的面积等于△BFG的面积，所以·（2m2-3），整理得2m4-9m2=0.又m＞0，则m=

二、“一题一课”教学微设计

教学目标：

1.回顾二次函数的相关内容：开口方向，图像与坐标轴的交点，顶点，对称轴等.

2.运用动态思维感受m值变化引起对应图像变与不变的量，同时感悟m值变化引起点动、线动、三角形的数与形的变化.

3.通过动态演示，培养学生提出问题、解决问题的能力.

4.注重解题策略的多样化及优化思想.渗透数形结合、方程、分类讨论、转化等数学思想方法.

重点：感悟m值变化引起图形的变化及两个三角形数与形的探究.

难点：第（3）题②中思维含量比较高，解决起来具有一定的难度.

教学过程：

教学环节（一）创设情境回顾旧知.

问题：已知二次函数y=x2-2x-3的图像（图略），你能获得什么信息？

师生活动：请一位学生说说，可以从开口方向，对称轴，与坐标轴的交点，顶点，增减性等方面进行回顾，教师及时板书.

追问：将y=x2-2x-3中的系数2变成m（m＞0），则y=x2-mx-3对应的图像哪些不变？（哪些变？）

【设计意图】创设开放性的问题情境，切口小，入口宽，让更多的学生参与进来，激发学生探究的兴趣，将系数2变成m（m＞0），引入参数后，引导学生感受变与不变的量，培养学生动态思维能力.

教学环节（二）问题呈现引发思考.

问题：抛物线y=x2-mx-3（m＞0）交y轴于点C，CA⊥y轴，交抛物线于点A，点B在抛物线上，且在第一象限内. BE⊥y轴，交y轴于点E，且BE=2AC.你能用含m的代数式表示图中的线段吗？

【设计意图】通过线段的表示，进一步运用二次函数的相关知识，在表示AC长度时学生可能利用抛物线的轴对称性得到，也可能用解析式求点的坐标，进而转化为线段的长度，培养学生解题策略的多样化.

教学环节（三）问题延伸尝试提问.

追问：连接AO并延长交BE的延长线于点D.此时，有什么值得研究的问题？

师生活动：先让学生展开动态思维的想象力，若有困难，教师可借助几何画板进行演示，在m值的变化过程中，感受图形的变化.

预设：1.点D在抛物线上时，m的值是多少？

2.某两条线段的长度相等时，求m的值.

3.△DEO与△AOC全等时，求m的值.

【设计意图】在动态几何中，引导学生尝试提出一些可探究的问题，培养学生提出问题的能力，在学生回答的基础上，引导学生提炼m变，引起点动、线动、形变（三角形），从而可探究点在某个特殊位置，一个三角形的形状（等腰三角形或直角三角形），两个三角形之间形（相似，全等）与数（面积）的关系.

教学环节（四）深入探究提升能力.

问题：刚才探究Rt△DEO与Rt△AOC两者的问题，若AG∥y轴，交OB于点F，交BD于点G，出现了新的Rt△BGF，此时，Rt△DEO与Rt△BGF又有什么值得研究的问题呢？

追问：若连接AE，交OB于M，此时新的△AMF与△BGF面积相等时，m的值是多少？

【设计意图】通过这两个三角形数与形的探究，渗透转化思想、分类讨论的数学思想方法，引导学生从多角度、多渠道解决问题，体现方法的多样化及优化.

三、教后反思

思想决定行动，思路决定出路.“以生为本，以师为导”的教学理念决定教学行为，数学课堂注重思维的训练，在问题设计中，通过设计开放性的问题情境，尝试让学生提出问题，并在问题解决中，注重一题多解，培养思维的发散性，同时渗透数学思想方法.

1.自主编题，完善学生的思维方式.

在教育改革不断深入的今天，通过自主编题开启学生自我思考之门，变被动做题到主动编题，变被动接受知识为主动获取知识，从而进一步自觉学习和感悟数学，真正成为数学学习的主人，是对所学知识的灵活运用，是创新思维的提炼和升华，是新课堂所追求的至高境界.作为新时代的教师，只有长期坚持对学生的培养和训练，才会使他们变成思维活跃、勤于观察、善于思考、敢于发言、勇于创新的人，也只有这样，我们的学生才会更自信，更乐于探究，我们的数学课堂才更富魅力！

2.关注学情，促成课堂的动态生成.

动态生成的前提是关注学情，孔子曰：因材施教！其实质就是关注学情！新课程标准强调：教师要能转变教育观念、教学方法；鼓励学生质疑问题，探究思考；让学生感受和体验数学知识产生、发展和应用的过程；启发学生发现问题和提出问题，善于独立思考，使数学学习成为再发现、再创造的过程.教师在教学活动中要保持一种开放的心态，采取多种多样的教学方法和手段，来促使学生充分展示自己的学习风采与个性.每一个学生都有发展的空间，具有进步的潜力，教师要积极鼓励学生充分发挥自己的优势，弥补自己的不足.焕发学生的创新意识和主体意识，更好地激发学生的学习热情，促进生成新的教学资源.

3.重视提炼，渗透数学的思想方法.

在复习课教学中，教师要及时引导学生进行提炼，提炼数学知识、思想方法、解题策略，挖掘动态问题中不变的量，同时要渗透各种数学思想方法.通过提炼、渗透，让学生能够从中理解知识点的内涵和外延，从反思过程中汲取经验教训，巩固和扩大解题成果，进一步提升学生思维的深刻性.

四、写在最后

初中数学复习课中，如果教师能够从一个题目（一般是课本的例、习题和中考试题）出发，开放性地设计问题，鼓励学生从多角度解决问题，并尝试让学生自主编题，提出问题，同时关注学情，动态生成，可让课堂更加自然，流畅.在这样一条复习主线下，提炼解题策略，挖掘数学本质，注重数学思想方法的渗透，真正让数学复习课成为学生的主阵地，走出“题海战术”的阴影，追求简约却不简单的课堂，还学生时空，体现“一题一课”的价值，真正凸显“以生为本”的教学理念.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

2.顾冷沅主编.初中数学教学研究［M］.上海：上海教育出版社，2012.

3.吴立建.数学课堂中应重视引导学生提出问题［J］.数学通报，2013（7）.

4.赵萍萍.“一题一课”走向简约的尝试——以2014年广东省中考第23题教育为例［J］.中学数学（下），2015（2）.

5.波利亚主编.数学的发现——对解题的理解、研究与讲授［M］.北京：北京科学出版社，2016.

6.俞卫胜.由博返约，追求简洁——一堂“一题一课”复习课的思考［J］.中学数学（下），2016（11）.

7.许燕.从解题赏析走向教学研究——以2016年无锡卷第27题教育为例［J］.中学数学（下），2016（10）.

8.张合远.追求自然、简约、深刻的思维课堂——以直角三角形的性质复习课为例［J］.中学数学（下），2017（1）.

9.俞卫胜.一题一课追求简洁，贵在自然［J］.中学数学（下），2017（2）.