以静制动自然生成
——以2016年甘肃省张掖市中考数学卷第28题为例
2017-04-24甘肃张掖市第三中学李永明
☉甘肃张掖市第三中学李永明
以静制动自然生成
——以2016年甘肃省张掖市中考数学卷第28题为例
☉甘肃张掖市第三中学李永明
一、问题的提出
“怎样解题表”是乔治·波利亚凝聚成的一套集解题思想、解题过程、解题思路、解题方法等于一身的一个完整的解题教学系统.它融理论与实践于一体,为学生提出问题、解决问题指明了方向.如何才能在中考压轴题中有效利用“怎样解题表”解决“动点问题”呢?按照“怎样解题表”指引,笔者结合2016年甘肃省张掖市中考数学卷第28题,从弄清问题、拟定计划、实现计划、回顾四个方面入手,认真反馈解题的思维过程,分析解题过程中的逻辑关系,使“怎样解题表”由常识上升为理论,让每个学生学会解题过程分析,提高解题能力.现拙文呈现其“四阶段”思维过程,以期抛砖引玉,与同行交流.
二、解题思维过程分析
原题:(2016年甘肃张掖第28题)如图,已知抛物线y=-x2+bx+c经过A(3,0)、B(0,3)两点.
(1)求此抛物线的解析式和直线AB的解析式.
(2)如图1,动点E从O点出发,沿着OA方向以1个单位/秒的速度向终点A匀速运动,同时,动点F从A点出发,沿着AB方向以个单位/秒的速度向终点B匀速运动,当E、F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
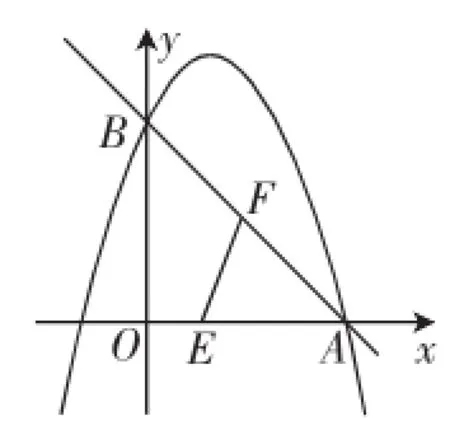
图1
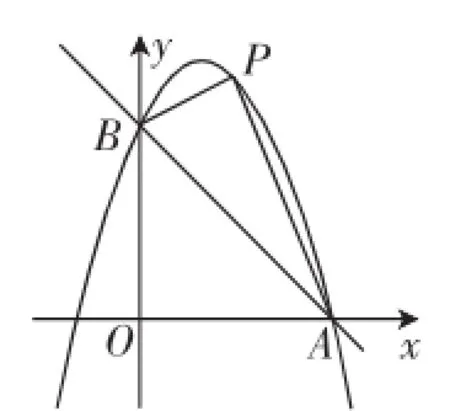
图2
(3)如图2,取一根橡皮筋,两端点分别固定在A、B处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A、B两点构成无数个三角形,在这些三角形中,是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标;如果不存在,请简要说明理由.
1.弄清问题.
“弄清问题”是解题的前提.在认真阅读题目后,必须分析本题的“未知是什么?已知是什么?条件是什么?满足条件是否可能?要确定未知,条件是否充分?或者它是否不充分?或者是多余的?或者是矛盾的?”
认真阅读例题,已知条件有三个:
抛物线y=-x2+bx+c的解析式;
抛物线经过点A(3,0);
抛物线经过点B(0,3).
未知有三问:
(1)第一问求此抛物线的解析式和直线AB的解析式;
(2)第二问当△AEF为直角三角形时,求t的值;
(3)第三问当△PAB的面积最大时,求点P的坐标.
2.拟定计划.
“拟定计划”是解题的关键,是一个探索解题思路的发现过程,也是一个化归过程.“你以前见过它吗?你是否见过相同的问题而形式稍有不同?你是否知道与此有关的问题?”
针对以上问题,要努力追忆在课本、资料中出现过的类似题目,从大脑中提取出与本例题有关的定义、公式、定理、类题等解题依据,把想到的与本题有关的信息都罗列出来,供下一步使用.
题型:求抛物线、一次函数解析式的题型;动点问题的题型;求三角形最大值问题的题型.
定义:正切的定义.
性质:相似三角形的性质等.
第(1)问:
问题思考1:从已知和未知条件思考:要确定抛物线y=-x2+bx+c和直线AB的解析式,只要知道什么就可以了?
已知抛物线y=-x2+bx+c的解析式中二次项系数a= -1,b和c未知,解析式中有两个未知数,所以确定解析式只需要知道两个点的坐标,就可用待定系数法求出其解析式.同理,直线AB的解析式也可用待定系数法求出.
问题思考2:从熟悉的题型思考:你以前见过它吗?你是否见过相同的问题而形式稍有不同?你是否知道与此有关的问题?你是否知道一个可能用得上的定理?看着未知数,试想出一个具有相同未知数或相似未知数的熟悉的问题.这是一个与你现在的问题相关,且早已解决的问题.你能不能利用它的结果和方法呢?
求解析式这类题经常练习,常用方法是待定系数法.
第(2)问:
问题思考1:从已知条件分析:你知道这是一个什么问题吗?第(2)问引入速度和时间后,你还能得到哪些条件?
它是一个双动点问题.E和F是两个动点,知道其运动速度和时间t,就可以把E和F两点的路程表示出来,即OE=t,AF=t.
问题思考2:你知道解决此类问题的方法吗?
解决此类问题的策略就是以静制动,运用以退求进的方法,退到特殊情况寻找突破口.也就是把动点E和F分别静止到△AEF为直角三角形时的特殊位置.
问题思考3:你知道△AEF为直角三角形的几种特殊位置吗?能画出草图吗?
△AEF为直角三角形一般有三种情况,但从图形上分析,∠EAF固定不变,如图3、4,所以有两种情况.

图3

图4
问题思考4:你见过这类型的题吗?你知道解决此题的方法吗?
这是常见的方程模型,由线段OE、OA的长求出线段AE的长,通过相似或三角函数列出方程,从而求出t的值.通过这种方法就把已知和未知两者联系了起来,使问题得到了解决.
第(3)问:
问题思考1:从未知条件分析:你知道这是一个什么问题吗?从整体上分析你认为点P存在吗?
第(3)问实质上也是一个动点问题,点P从点A出发,在抛物线上移动到达点B,△PAB的面积逐渐增大,又逐渐减小,在这一连续的过程中,一定有一个最大值.
问题思考2:在点P的运动过程中你发现了哪些不变的量?哪些变化的量?
线段AB的长不变,△PAB中边AB上的高在变化.
问题思考3:你见过这种类型的题吗?解决此题的关键是什么?如何解决?
见过,解决的关键是确定点P在什么位置时,△PAB的面积最大.从图上可以分析,在△PAB中,线段AB的长是固定的,当△PAB中AB边上的高达到最大值时,△PAB的面积也最大,也就是说可以向上平移直线AB,如图5,平行线与抛物线有两个交点,利用平行线间的距离处处相等,当直线AB平移到与抛物线只有一个交点时,如图6,△PAB中AB边上的高达到最大值,这时就找到了点P的准确位置,通过已知条件的变换,找到了点P,它是存在的.下面还得求出点P的坐标,抛物线的解析式与平移后的直线的解析式组成方程组,当有一个交点时,Δ=0,求出t的值.
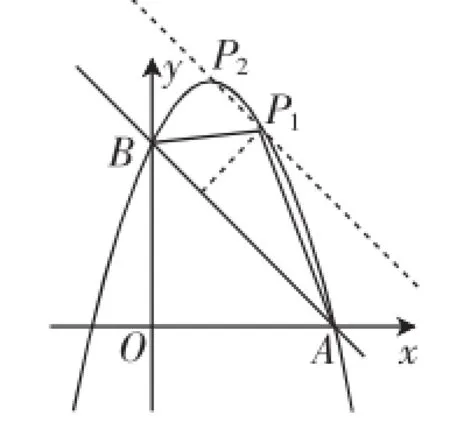
图5

图6
3.实现计划.
解:(1)由抛物线y=-x2+bx+c经过A(3,0)、B(0,3)两
(3)如图7,存在.
过点P作PC∥AB交y轴于C.设直线PC的解析式为y=-x+b.由得-x+b=-x2+2x+3,则x2-3x+b-3=0.
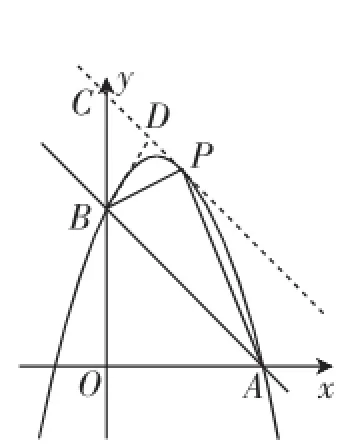
图7
过点B作BD⊥PC,则直线BD的解析式为y=x+3,
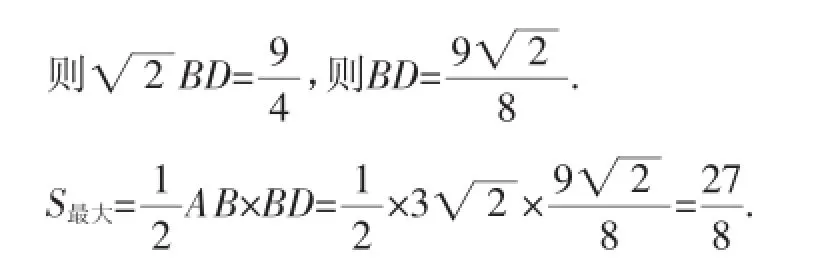
4.回顾.
解题后的回顾是对解题过程的反思,从中发现新的解题方法,提炼解题思想,形成对未来有指导作用的解题经验,升华为学生分析、加工和运用信息的数学才能,从而提高学生的解题能力.
(1)从正面检验每一步,推理是否有效,演算是否准确.再做特殊性检验,由结论出发,由抛物线y=-x2+2x+3和直线y=-x+3,令x=0,得到y的值都是3,进一步与点B(0,3)的横、纵坐标对比,如果都一致,说明正确.
(2)回顾解题过程可以看到,首先要弄清问题,分析已知和未知,简化已知条件,并从图形和记忆中提取有用信息,并相应将两组信息资源做合乎逻辑的有效组合.这当中,起调控作用的关键是如何去构思出一个成功的计划(包括解题策略),也可以根据自己的解题经验进一步领悟制定计划的普遍建议或模式.
(3)在解题方法上,它是分析法的成功应用,对于第(2)问,由结论出发,由后往前找成立的充分条件,求出t的值,我们只需画出t值存在的两种情况的草图,用t的代数式表示出线段AE、AF的长,通过相似或三角函数列出方程,从而求出t的值.
(4)在解题思想上,它是方程思想的成功应用,三个小题都用到了方程思想,第(1)问为了求解析式,列出了二元一次方程组.第(2)问要求t的值,要列出一个分式方程来解,难度进一步加大.第(3)问要求点P的坐标,要列一个二元二次方程组,根据化解后的一元二次方程根的判别式,求出点P的坐标.
(5)“你能否用别的方法导出这个结果?”在信念上我们应该永远坚定地做出肯定的回答,虽然你没有实现,但这只是能力问题或暂时现象.对于第(3)问,还有以下解法.

图8
方法2:如图8,过点P作y轴的平行线,交直线AB于点G,交x轴于点M,过点B作BN⊥PG,这样我们可以把△PAB分成△PAG和△PBG两个三角形,由图形可知△PBG和△PAG边PG上的高分别是线段BN和AM,BN+AM=OA=3是个常量,只要求出PG的最大值,即可得△PAB的最大值.设点P(m,-m2+2m+3),由题意知点G的坐标为(m,-m+3),所以PG=-m2+2m+3-(-m+3)=-m2+3m.S△PAB=3),当m=-,此时点时,△PAB的面积最大,最大是P(,).

图9
方法3:如图9,可以用分合并用的方法,将△PAB的面积转化为四边形PAOB的面积减去△OAB的面积,四边形PAOB的面积等于△OBP的面积加上△OPA的面积.设点P为(m,-m2+2m+3),S△PAB=S四边形PAOB-S△OAB=-时,△PAB的面积最大,最大是,此时点P(,).
三、反思小结
综述以上解题过程,解答一道题,第一件事就是想知道:这是道什么题?它是什么形式,属于哪种类型?如果识别了其类型,就得到了解题方法,因为在课本里,许多类型的习题都有它们特定的解题方法和策略.例如,模式识别,映射化归,数形结合,差异分析,分合并用,动静转换,进退互化,有效增设,正反相辅,以美启真等.如果识别的类型不是我们熟悉的类型,我们不知道其解题方法,那么,我们应该怎么办呢?只有归结为熟悉的早已解决的问题,利用变换、改编或其他方法,最终化归为已经解决的问题.如果遇到不熟悉的和费解的问题,那么,所有已知的建议都无济于事了,这时寻找解题思路有两种方法:一种方法是把问题“分解”,使每一个小问题都是熟悉的;另一种方法是可以揭示问题的深层结构,使问题的实质是熟悉的,还可以不间断地改编问题,最终化归为已经解决的的问题.
总之,解题就是把题目归结为已经解过的题,是一个改编习题的过程.我们只有不断地去弄清问题、拟定计划、实现计划、回顾反思,对已知和结论不断地去分析,找到它们的联系,才能找到一个简洁、高效的解题方法.
1.罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2008.
2.罗增儒.中学数学解题[M].南宁:广西教育出版社,2008.
3.李永明.捕捉、提取、组合、反馈四阶段解题的思维剖析与思考——以2014年张掖卷第28题为例[J].中学数学(下),2015(7).
