对湖北省2016年一道中考试题的质疑

☉湖北仙桃荣怀学校初中部陈木昌

对湖北省2016年一道中考试题的质疑

☉湖北仙桃荣怀学校初中部陈木昌

湖北省随州市2016年中考数学试题第22题是一道有关圆的证明和计算的解答题，原题目和参考答案如下：

如图1，AB是⊙O的弦，点C为半径OA的中点，过点C作CD⊥OA交弦AB于点E，连接BD，且DE=DB.

（1）判断BD与⊙O的位置关系，并说明理由；

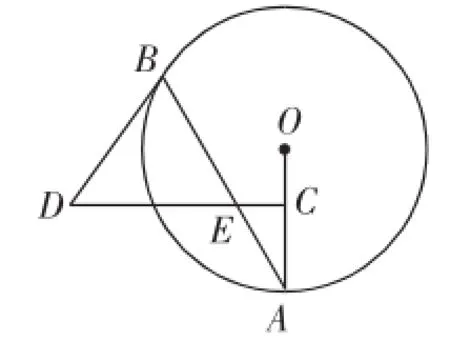
图1

【解答】（1）如图2，连接OB.由OB=OA，DE=DB，得∠A=∠OBA，∠DEB=∠ABD.

由CD⊥OA，得∠A+∠AEC=∠A+∠DEB=90°.

则∠OBA+∠ABD=90°，则OB⊥BD，则BD是⊙O的切线.

（2）如图2，过点D作DF⊥BE于点F.

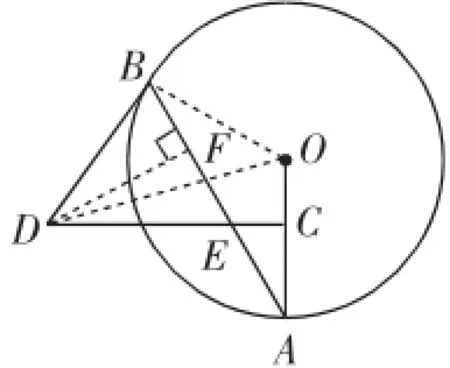
图2

易证∠EDF=∠A.

则CE=CD-DE=15-13=2.

笔者在做第（2）题时发现，不用BE=10这个条件，可求出⊙O的直径，过程如下：

连接OD，设⊙O的半径为r.在Rt△ACE中，tan A=，根据OD2=解得r=

于是我又尝试不用CD=15这个条件求⊙O的直径.过程如下：

为什么会产生上述截然不同的结果呢？本小题中，在tan A=这个条件下，CD=15和BE=10这两个条件只需一个就可求直径，那么由上面推导可知结论不一致，只能说明这两个条件是互相矛盾的，线段DC与BE的长是否满足某一数量关系呢？

按以上思路设CD=x，由DB2+OB2=DC2+OC2，得r.设BE=y，则EF=BE=.在Rt△DFE中，tan∠FDE=tan A=5，因此EF∶DF∶DE= 12 5∶12∶13，DE=y.由DB2+OB2=DC2+OC2，得（）2+r2=