模考题讲评：由浅及深·渐次推进·变式检测——以中考模考把关题讲评为例

☉福建大田县第五中学叶钟布

模考题讲评：由浅及深·渐次推进·变式检测
——以中考模考把关题讲评为例

☉福建大田县第五中学叶钟布

中考模考题讲评是中考复习的一项重要教学任务，如何取得高质量的讲评效果，也是我们共同的追求.本文以一道中考模考把关题为例，先给出该题的思路突破和解后反思，再给出该题的教学微设计，供研讨.

一、模考题的思路突破与解后反思

模考题：如图1，矩形ABCD中，AB=3，BC=4，点E是射线CB上的动点，点F是射线CD上一点，且AF⊥AE，射线EF与对角线BD交于点G，与射线AD交于点M.

（1）当点E在线段BC上时，求证：△

AEF∽△ABD；

（2）在（1）的条件下，连接AG，设BE=x，tan∠MAG= y，求y关于x的函数解析式，并写出x的取值范围；

（3）当△AGM与△ADF相似时，求BE的长.

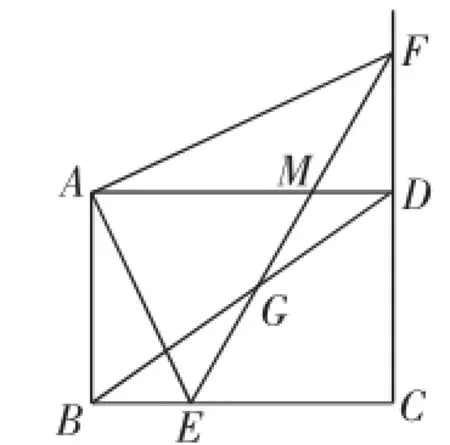
图1

思路突破：

（1）分析证明△AEF∽△ABD的条件，发现只能顺利找到一组角（∠BAD与∠EAF）对应相等，但是缺少其他对应角的直接发现，转向寻找边之间的比例关系，会有新的发现，可以由△ABE∽△ADF，得，而这组对应边成比例的式子恰恰也可作为△AEF∽△ABD的重要条件，于是证明思路获得贯通.

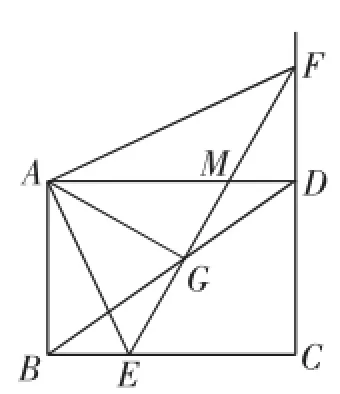
图2

（2）如图2，如果在△MAG中思考，需要猜想该三角形是否为直角三角形.如何确定是直角三角形呢？只需要证出△AMG∽△FMD，即需要证出.而由（1）中△AEF∽△ABD可得∠AFM=∠ADG，结合对顶角∠AMF=∠DMG，可证出△AMF∽△GMD.于是贯通思路.接下来就可以“等角转化”，即tan∠MAG=tan∠MFD，思考MD与DF的比值即可.借助△ABE∽△ADF，得，把数值、参数代入比例式，可得.接下来攻克“如何用含x的式子表示MD”.可以考虑△FMD∽△FEC，得，把数值、参数代入比例式，可得于是待求的

解后反思：事实上，在图2中，我们发现了∠AGM=∠FDM=90°，根据90°的圆周角所对的弦是直径，可以确认A、G、D、F四点共圆（且是在以AF为直径的圆，如图3）.如果能基于四点共圆的高观点，也可利用“同弧所对的圆周角相等”快速转化得tan∠MAG=tan∠MFD.

（3）该题放开点E的运动位置，需要考虑点E在线段BC、线段CB的延长线上时的不同情况.先考虑点E在线段BC上，这时有一个难点是△AGM与△ADF相似时，需要明辨它们的对应关系.这是两个直角三角形，所以只需要考虑两个锐角的不同对应关系，而由于∠AMG是△AFM的一个外角，所以∠AMG只能对应∠AFD，故这两个三角形相似时，只有一种对应关系，即△AGM∽△ADF.

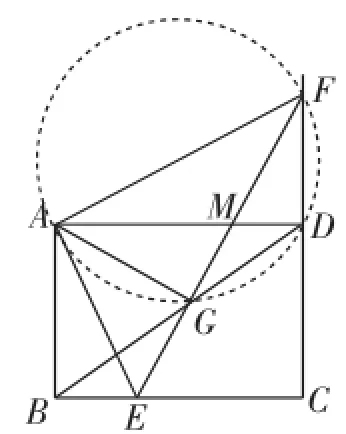
图3

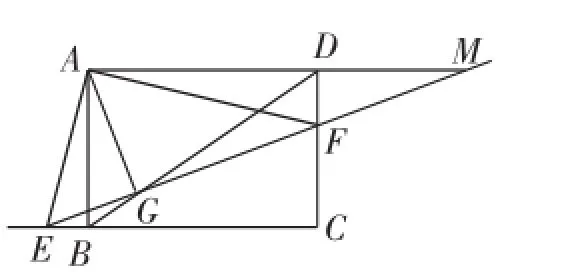
图4

解后反思：图4中，仍然有A、G、D、F四点共圆（且是在以AF为直径的圆上），并且此时点D恰为AM的中点！

二、解题教学的微设计

教学环节（一）预热问题.

例1题干同上文“模考题”，当点E在边CB上时，

（1）求证：△ABE∽△ADF；

（2）求证：△AEF∽△ABD；

（3）连接AG，求证：△AGM∽△FDM；

（4）有人发现A、G、D、F四点在同一个圆上，你觉得有道理吗？为什么？

教学环节（二）拾阶而上.

例2题干同上文“模考题”，点E仍在线段BC上，连接AG，设BE=x，tan∠MAG=y.

（1）当x=1时，求y的值；

（2）当E为BC的中点时，求y的值；

教学环节（三）挑战难题.

例3题干同上文“模考题”，当△AGM与△ADF相似时，解决下列问题：

（1）当点E在线段BC上时，有人说只存在一种可能：△AGM∽△ADF，请分析“这种推定”是否正确；

（2）当点E在CB的延长线上时，你觉得△AGM与△ADF相似时，对应关系有几种可能？为什么？

（3）求BE的长.

教学环节（四）变式再练.

变式题：如图5，矩形ABCD中，AB=3，BC=4，点E是射线BC上的动点，点F是射线BA上一点，且DF⊥DE，射线EF与对角线AC交于点G，与射线DA交于点M.

（1）当点E在线段BC上时，求证：△DEF∽△DCA；

（2）在（1）的条件下，连接AG，设CE=x，tan∠MDG= y，求y关于x的函数解析式，并写出x的取值范围；

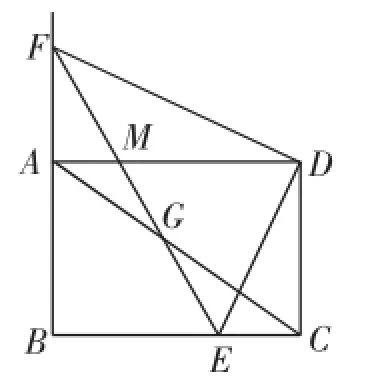
图5

（3）当△DGM与△DAF相似时，求CE的长.

变式意图：为了检验听课效果，只是对模考题进行图形位置的变换，其余数据、设问方式都没有改动，但是学生已不可能照着原来的解答简单改写，而是需要另外构图并组织语句，能有效检测听课效果.

三、进一步的思考

1.深入思考并解读模考把关题的命题意图.

各个地区的模考题往往都是命题组深入构思，贴近本地区命题风格的模拟题，所以讲评前教师务必深入思考并解读出这些模考把关题的命题意图，不同小问之间的关系是递进亦或并列，有时第（1）小问解答是轻松的，但是如果没有深入反思或进行成果扩大，则对后续问题求解是不利的，甚至难以获得思路突破.上文在模考题第（1）问的解答之后，我们曾给出反思回顾，并反思出四点共圆的结构，该四点共圆在后续问题的探究中都有体现.

2.围绕模考题开展“一题一课”教学微设计.

近两年来的《中学数学》（下）有大量涉及考题研究的案例文章，这些文章多数不满足于解题思路的获得、一题多解的探究、多解归一的结构揭示，而是从解题研究走向解题教学，设计了很多优秀的教学微设计，对于教师读者来说，很方便就可拿到课堂教学中去直接开展相关教学.受此启发，笔者在上面也实践跟进，给出“一题一课”教学微设计，试图从简单情形入手，将难点进行分解，各个突破，最后迎难而上，挑战难题.

3.将模考题简单改编变式后反馈听课效果.

对于难题讲评来说，如果只是教师分析得详实、变式丰富，常常是很多学生感叹于教师对一道试题研究之深，但更多学生虽然听懂了，独立再做却还是有很多障碍点难以通过，一个有效的反馈方式是开展变式再练，像上面我们只是把模考题的图形位置进行简单变换，数据没有变化，甚至对应的字母也没有改编，如果学生真正听懂了，应该可以独立演算出来，可有效检测和反馈教学效果.

1.孙莉.思路生成贵在自然，一题一课追求简约——一道考题的思路突破与习题课设计［J］.中学数学（下），2016（9）.

2.朱国生.反思考题难点，预设“一题一课”——以2016年江苏南通中考卷第28题为例［J］.中学数学（下），2016（9）.

3.吴忠妙.一道考题的思路、难点与教学设计［J］.中学数学（下），2016（9）.

4.付小飞.明辨并列与递进，引导分离和聚焦——2016年江苏苏州中考第28题解析与教学思考［J］.中学数学（下），2016（7）.