聆听数学的音律，发现学习的美好

☉广东广州市第一一三中学蒋霞

聆听数学的音律，发现学习的美好

☉广东广州市第一一三中学蒋霞

学习数学知识的过程就像是在吟唱一首动人的歌曲.正如一个个音符构成了歌曲的旋律一样，一个个基础知识也堆积构建成了初中数学的知识大厦.这里所说的堆积并不是简单的罗列，而是需要加入学生们的头脑判断与思维整合.因此，初中数学的学习过程并不是机械乏味的.融入了学生们的主观处理之后，运用我们的心灵去切实感受，便会发现数学学习之中的美好之处，正如歌曲里面的动人音律一样醉人.

一、从细节处看数学，发现学习的严谨之美

想要学好初中数学，需要学生具备很强的细心特质.很多重要的知识点往往都会潜藏在文字与公式的角落之处，稍有粗心，便会遗漏，造成知识学习的严重漏洞.这种对于知识细节的关注，不应当成为学生开展学习时的思想压力，而要想办法由此呈现数学学科的严谨之美.

例如，在对线段部分的知识进行教学时，我在课堂中引入了这样一个问题：已知线段AB的长为6，线段BC的长为4，且点A、B、C在同一条直线上，那么，线段AC的长度是多少？看似简单的一个问题，却并不是那么容易答对的.结合线段的基础知识来分析，便可以发现，点C的位置有两种可能，即在线段AB上（如图1）或在AB的延长线上（如图2）.这个问题很明确地展现出了数学学习对于细节的强调.

图1

图2

放低视野，从细节之处看待数学，便会看到初中数学中十分显著的严谨之美.抓住一个细节，或从一个小处切入，就可以看到数学知识的特点，甚至引发学生对深层次内容的思考.从语言到思维的高度严谨，不得不说是初中数学学习的魅力所在.

二、从方法处看数学，发现学习的规律之美

初中数学中的知识内容虽然繁多，学习起来却不是毫无章法的.一次高效率的知识学习，甚至不需要把精力分散在对每一个知识内容的雕琢上，而是通过掌握相关的数学思想方法，实现对具体知识点的统领性掌握.这种学习方法上的思维捷径，就是初中数学中所蕴含的规律之美.

例如，在对整式的内容进行教学时，我向学生提出了这样一个问题：已知x-3y=-3，那么，5-x+3y的值是多少？如果按照常规的处理方法，想要通过一个已知条件就将x和y的值分别求解出来，显然是不可能的.这时，就需要运用整体代入思想，以5-x+3y=5-（x-3y）的方式构造出x-3y的形态，问题便可迎刃而解.这种思想方法在初中数学问题的分析推导过程中的应用是非常广泛的.这一方法的成功总结，为学生的数学思维开辟出了一条新路.

我们常说的对数学进行探究，指的不仅仅是对具体知识内容的逐个推敲，还包括对规律方法的总结和提炼.相比而言，后者的站位显然更高.当学生具备了从规律方法处掌握数学的意识之后，整个知识探究过程将会明显简化，探究效果也会得到升华.从方法处入手掌握具体知识，就是初中数学学习中的规律之美.

三、从应用处看数学，发现学习的实践之美

数学学习的美好并不仅仅存在于理论性的知识方法中，更反映在我们身边的实际生活里.细心观察便会发现，很多实际生活中的问题都可以运用数学里的思维方法加以解决.当理论与应用巧妙结合之后，学生便会在学以致用的过程中更好地理解数学，并在实践的同时发现数学的美好.

例如，在对统计的内容进行教学时，我带领学生一起思考了这样一个问题：小明对自己所在城市的气温进行监测记录，并将3月1日至8日的最高气温变化情况绘制成了图3所示的折线统计图，并将该图中的数据进一步整理成了图4所示的统计图.那么，通过观察这两幅统计图，请试着回答下列问题：（1）图4中缺少的部分有哪些？（2）在小明进行监测的这8天中，最高气温的中位数是多少？（3）这8天中，最高气温的平均数是多少？上述问题所产生的背景，就是学生的真实生活.这种问题研究方式，也是学生在各种学科调研中经常接触的.由此，学生从实际应用中发现了数学统计的影子，对这部分知识的探究热情瞬间提升了不少.

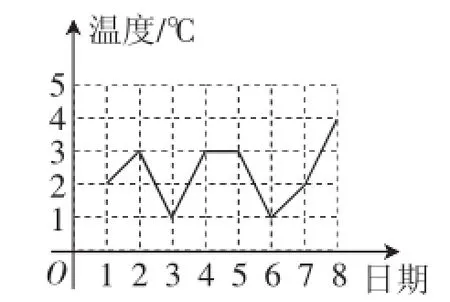
图3

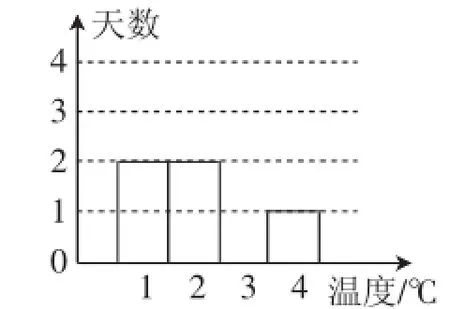
图4

从应用的角度看待数学，对于初中数学教学来讲有两个方面的价值：第一，用自己当前所掌握的理论方法去解决存在于身边的实际问题，能够为学生增加自信，进而更加积极主动地投入接下来的学习过程中去；第二，通过应用的方式展现理论知识，为学生提供了另一个理解数学的途径.数学知识方法在实践中所体现出来的魅力，将会成为学生继续学习的兴趣与动力.

四、从开放处看数学，发现学习的灵动之美

数学知识是灵活的、动态的，正如音律的变化跳跃一样.因此，为了触摸初中数学的精髓所在，学生不能只停留在教材中的内容范围之内，更要走出基本内容的禁锢，让思维遨游在更加开放、广阔的天空里.由此，将教学内容加以开放，也就成为了高效的初中教学所需要的设计.这种设计也能够让学生意外地看到属于初中数学的灵动之美.

例如，在对三角形的内容进行综合性练习时，我为学生设计了这样一个问题：已知，在等腰Rt△ABC和等腰Rt△AED中，∠ACB和∠AED均为直角，AD与AC等长.（1）请大家试着探索，如图5，当点E在AB上，且点C和点D重合时，如果点M和点N分别为DB和EC的中点，那么，MN和EC的位置关系是什么？二者之间的数量关系又是什么？（2）请继续进行探究：如果将上述△AED绕着点A旋转到图6所示的位置，分别连接DB和EC，以及二者的中点M、N，那么，MN和EC之间的数量关系与位置关系是否会发生变化？如果有变化，请说明你的理由；如果没有变化，请在逆时针旋转45°后的图形（如图7）基础上证明位置关系不变，在顺时针旋转45°后的图形（如图8）基础上证明数量关系不变.这种开放的设问方式让学生们看到了数学的灵动，思维的美感展露无遗.

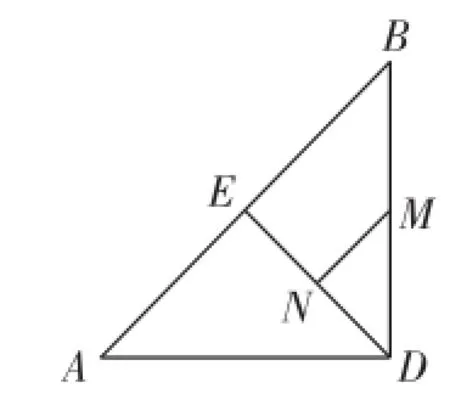
图5

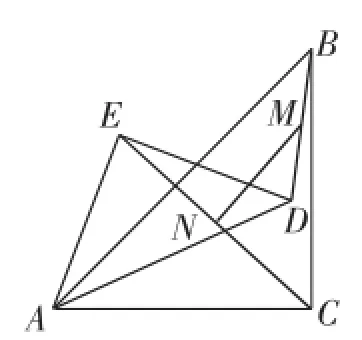
图6

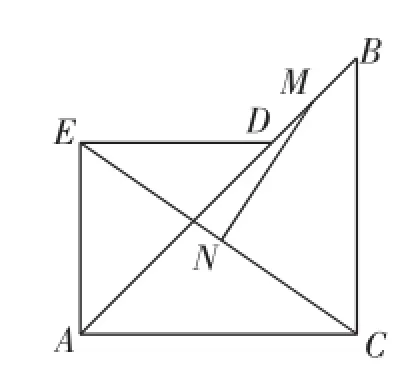
图7

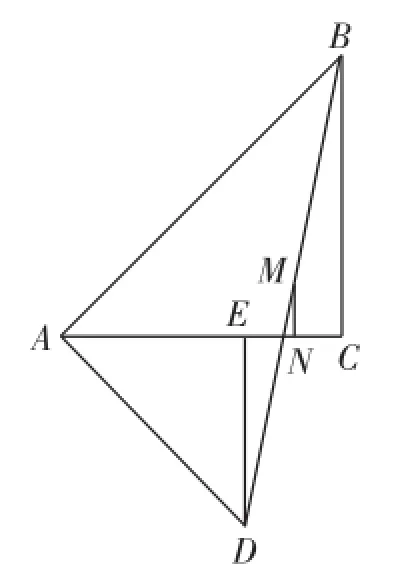
图8

很多学生接触开放性的数学知识，都是直接在各种测验中开始的.这种出现方式，往往会让大家在应试的压力之中对开放性知识学习产生误解，认为这些内容都是晦涩、枯燥，且难度很大的，产生抵触心理也是很自然的.如果能在平时的教学中时常加入开放性的元素，并对学生的分析思维进行引导启发，让大家用美好的眼光看待开放的数学，教学效果自然截然不同.

从不同的角度着眼，我们可以发现属于初中数学的多种美好，这也构成了数学学习的综合魅力.要想让学生从内心深处产生对数学学习的热情与热爱，就需要启发大家发现这个学科的美好之处，引导大家对数学知识爆发热情，方能从根本上触发其主动学习的动力.初中数学的美好体现在每个知识角落当中.希望教师能够从这个角度出发，向学生展现数学更多的引人之处，为高效的初中数学教学开辟新思路.

1.李树臣.论形成和发展数学能力的两个根本途径［J］.中学数学教学参考，2002（9）.

2.朱海瀚.精彩的课堂源于教师的智慧［J］.数学学习与研究，2012（2）.

3.李树臣.浅谈国际中学数学教育发展的主方向［J］.中学数学，2001（9）.

4.张胜利.数学概念的教科书呈现研究［D］.东北师范大学，2011.