巧设计呈经典探无穷*——一道期末原创题的命制过程及感悟

☉江苏南京师范大学附属中学新城初中何君青

☉江苏南京师范大学附属中学新城初中陈敏婕

巧设计呈经典探无穷*
——一道期末原创题的命制过程及感悟

☉江苏南京师范大学附属中学新城初中何君青

☉江苏南京师范大学附属中学新城初中陈敏婕

《义务教育数学课程标准（2011年版）》在评价建议部分明确指出：评价不仅要关注学生的学习结果，更要关注学生在学习过程中的发展和变化，在书面测验中，更要积极探索可以考查学生学习过程的试题，从而了解学生的学习过程.上述建议，无疑给命题提出了更高的要求.期末考试作为一学期最后一次考试，不仅对学生本学期的学习情况要作出评价，也对教师本学期的教学起到了衡量作用，所以对于期末考试，无论是学生还是教师都相当重视.近期，笔者命制了建邺区九年级上学期期末考试试卷，压轴题以“新定义“的探究题为背景，将一个“经典的定理”加以变形、推广、延伸，得到了全区老师的称赞.命题过程中有些许心得，故撰文与同行分享.

一、原题呈现

问题提出

若一个四边形的两组对边乘积之和等于它的两条对角线的乘积，则称这个四边形为巧妙四边形.

初步思考

（1）写出你所知道的四边形是巧妙四边形的两种图形的名称：________，________.

（2）小敏对巧妙四边形进行了研究，发现圆的内接四边形一定是巧妙四边形.

如图1，四边形ABCD是⊙O的内接四边形.

求证：AB·CD+BC·AD=AC· BD.

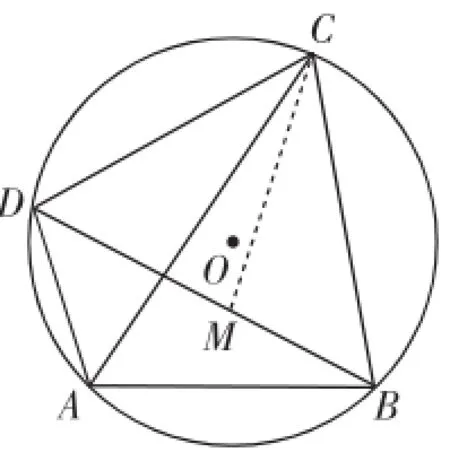
图1

小敏在解答此题时，利用了“相似三角形”进行证明，她的方法如下：

在BD上取点M，使∠MCB=∠DCA.

（请你完成小敏的证明过程.）

推广运用

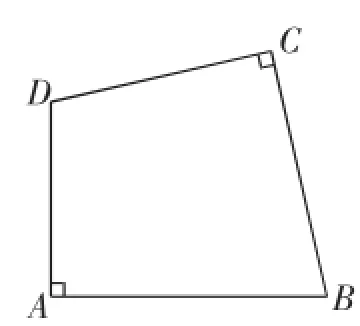
图2

二、命题过程

1.拟定计划.

近几来，全国各地的中考试卷时常出现“即时学习”型试题.这些试题立意鲜明、情境新颖、设问灵活，让学生在考场里即时学习一个新概念、新名词，现学现考，反映学生对已有知识的掌握程度及应用数学知识解决问题的能力.南京市2016年中考的最后一题就是“即时学习”型试题.为了与南京中考命题风格保持一致，笔者初步计划将此份试卷的压轴题定位为“即时学习”型试题，争取达到题型新、理念高的标准.定了题型后便要思考考查什么内容，由于试卷中笔者已经出了一道新颖的二次函数题，考虑到九年级几何部分主要以圆、相似为主，所以笔者决定此次期末试卷的最后一道几何压轴题以圆、相似为载体进行考查.

确定了题型和考查内容后，笔者翻阅了《义务教育数学课程标准（2011年版）》，仔细研读圆、相似的考查要求，对圆的考查主要以圆的相关概念、直线与圆的位置关系为主，对图形的相似的考查主要以相似三角形的判定定理和性质定理为主.基于此要求，鉴于此题为压轴题的定位，笔者决定命制一道难度系数为0.35的“即时学习”型试题，题目预设3~4问，逐步递进，涵盖填空或选择、证明、解答或探索，让不同层次的学生都可以得到适合自己的分数，又能让优秀的同学凸显出来.

2.初稿形成.

计划拟定后，笔者翻阅各套教材，寻找适合的出题资源，收获不大，因为教材中的题目都是再熟悉不过的.于是笔者查阅《几何原本》和百度寻找突破口，托勒密定理引起了笔者的注意：圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.

有了托勒密定理后，为避免被套上考一个学生没有学过的定理的“帽子”，笔者决定题目中不出现托勒密定理这些词汇，将以此经典定理为背景，赋予它新的生命，重新让它绽放光彩.很快笔者第一稿完成，如下所示：

问题提出

若一个四边形的两组对边乘积之和等于它的两条对角线的乘积，则称这个四边形为巧妙四边形.

初步思考

（1）小敏对巧妙四边形进行了研究，发现圆的内接四边形一定是巧妙四边形.

如图1，四边形ABCD是⊙O的内接四边形.

第一稿时，笔者并没有想到比较满意的第三问，仍然在积极的思考中.

3.打磨完善

本着设身处地为学生考虑的原则，作为学生我要是看到这个压轴题，一定无从下手，瞬间放弃，因为第一问想很久可能也想不出来.故思虑再三，决定适当降低难度，将圆的内接四边形一定是巧妙四边形进行适当铺垫，这样每个层次的学生都有得分的可能.

为了符合南京市的中考风格，既然起了一个赋予美感的新名字，那就不如让一类四边形串起来，故笔者决定在一稿中再加入第一问，让学生重新认识一下以往学过的四边形，这样难度又降下来了.于是加了一问：写出你所知道的四边形是巧妙四边形的两种图形的名称：_______，_______.这样题目就有三问了，也不用苦思冥想最后一问了.至此，此题可算基本命制完成.

从考查形式上看，本题是“即时学习”型试题，形式新颖，又有填空、证明、探索，比较全面；从考查内容上看，本题以考查圆和相似这两个“图形与几何”中的重要板块为主，注重对基础知识、基本技能的考查，也注重对数学思想的考查，同时又涉及对数学活动经验积累的考查；从考查意义上看，本题考查的知识连贯性很强，将圆、四边形、相似三角形紧密相连，提醒教师授课时关注知识间的连贯性教学.而且本题解法多样，学生可以从多角度思考问题、解决问题，有利于学生思维能力的发展.所以，此题是一道不可多得的好题.

4.回顾反思.

回顾命制此题的过程，一波三折，多次推敲、打磨、修改，确实不易.但值得肯定的是，此题独辟蹊径，将一个很多教师曾经关注却未曾深究的定理呈现出了不同精彩，定然会成为一个经典，也会有无限探究的价值.可是笔者还觉得存在遗憾，如果能再加以发展，将该题的研究领域赋予一个现实背景，解决更多的生活问题就更完美了，介于命题时间有限、题目考查容量限制，未曾考虑，确实可惜.

推广运用

如图2，在四边形ABCD中，∠A=∠C=90°，AD=

三、命题感悟

1.命题策略.

很多教师命题时总是感觉无从下手，不知道如何命题，尤其是像期中、期末这样大型的统考试题的命制，命题时间短，人力有限.于是很多出卷教师为了完成任务，常常会将其余省市的中考题或期中、期末考试题直接拿来或者简单改动几个数字，这样会把广大备考师生引向题海，认为多做题就能做到类似的题目，使得考试的导向走偏.事实上，试卷中的题型可以分为基础题、中档题和探索研究题.简单题用陈题是可以的，这部分题目主要以考查基础知识和基本技能为主，要注重考查学生对这些知识所蕴含的数学本质的理解；中档题就应该有一些原创的成分了，这部分题应该是考查学生对数学知识的理解程度，考查学生能够在具体情境中合理应用，可以在一定程度上改编陈题，可采用条件一般化法、联系实际法、更换背景法、转换题型法等方法；探索研究题尽可能全部原创，这样才能真正达到诊断的作用，检测出学生学习过程和教师教学过程中存在的问题，为备考师生指明日后学习的正确方向，这些题在命题时，要淡化特殊的解题技巧，不要出现偏题、怪题，要重视数学活动经验积累的考查、数学思想的考查，以及数学核心素养的考查，真实、有效地检测出学生数学的真正能力.

2.命题意义.

命制试题时，教师一定要了解这份试卷的命题意义，考查作用是什么，比如期中、期末考试和中考就有很大区别.期中、期末考试的目的是为了改善教与学的关系，从而达到共赢局面，通过考试，教师可以发现教学工作中存在的不足，从而加以重视、改进、提升，学生可以发现自己对某些知识掌握的问题，从而加以关注、完善、提高，故期中、期末考试前，命题老师要结合当地中考的命题风格，了解本学段及本学区学生容易出现的问题，把握好考试的方向，命制难度系数约为0.75的试题，考试后，教师、学生要客观地分析从考试中发现的不足，加以改进.中考的目的是为了检测三年学习的状况及为高一级学校选拔学生，也对当地日后的教学起指导作用，所以这部分试题一定要达到公平、公正，力求大幅度原创，在设计试题时，要结合多方面因素进行命题，难度系数约为0.7.

无论如何，命题都是一件十分辛苦的事情.教师想把题命好，一定是一个长期的过程，源于平时的积累，更要注重教学过程中的收集、命题前的深入研究、命题后的反思总结.所以，要从巧妙的题目设计开始，呈现出经典的试题，带给广大师生无限思考、探索的空间，让命题真正超值、教学真正行之有效.

*本文系南京市教育科学“十二五”规划立项课题“‘跑班’分层模式下初中数学课堂教学与考试评价研究”（课题编号：L/2015/ 181）的阶段性成果.