一道中考压轴题命题立意的再探讨

☉江苏常熟市实验中学沈叶柯

一道中考压轴题命题立意的再探讨

☉江苏常熟市实验中学沈叶柯

一、问题呈现

江苏省某市某年度中考第27题是压轴题，原题如下：

已知梯形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3.

问题1：如图1，P为AB边上一点，以PD、PC为边作平行四边形PCQD，请问：对角线PQ、DC的长能否相等？为什么？

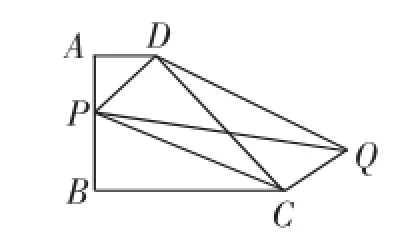
图1

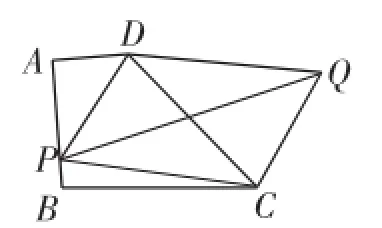
图2

问题2：如图2，若P为AB边上一点，以PD、PC为边作平行四边形PCQD，请问：对角线PQ的长是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由.

问题3：若P为AB边上任意一点，延长PD到E，使DE= PD，再以PE、PC为边作平行四边形PCQE，请探究对角线PQ的长是否也存在最小值.如果存在，请求出最小值；如果不存在，请说明理由.

问题4：如图3，若P为DC边上任意一点，延长PA到E，使AE= nPA（n为常数），以PE、PB为边作平行四边形PBQE，请探究对角线PQ的长是否也存在最小值.如果存在，请求出最小值；如果不存在，请说明理由.

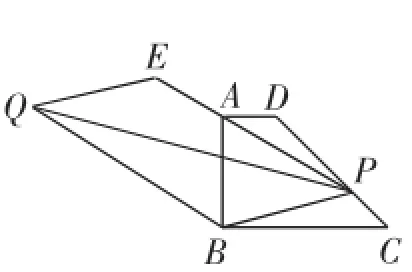
图3

本题属于动点问题，主要的考点有全等三角形的判定与性质、相似三角形的判定与性质、一元二次方程根的判别式、勾股定理、平行四边形的判定与性质等知识点；以极值问题为切入点考查数学结论存在性问题的一般解题思路和方法.解答本题需要较强的几何直观能力、空间想象能力和逻辑推理能力，笔者在和学生一起探究这个问题时，时常被图形搞得眼花缭乱，难以分清其中三角形、线段、角等基本几何元素之间的数量及位置关系.

2015年4月19日，华东师范大学张奠宙先生在“中国数学教育之友初中”QQ群的在线讨论中认为，中学的平面几何主要目的在于培养学生的逻辑思维能力，训练的深度不宜太深，当用平面几何的方法难以解答时，可以尝试用解析几何的方法去理解和思考，这也是几何学发展的整体方向.笔者有幸参与了这次讨论，聆听了张老先生的教诲.当第二天再看这个问题时，立即想到何不用解析几何的方法试试呢？

二、探究过程

问题1是这道题的破题之问，容易上手.假设四边形PCQD为矩形，易证Rt△APD∽Rt△BCP，于是有AD∶BP= PA∶BC，AD、BC已知，PA+PB=AB也是已知，这样就得到了一个关于PA（或PB）的一元二次方程；根据判别式判断这个一元二次方程没有实数解，因此四边形PCQD不可能为矩形.

图4

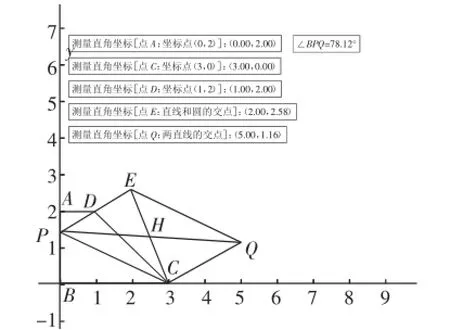
图5

根据题意，自然想到建立坐标系比较简单的办法就是以B点为原点，以BC所在直线为x轴，以AB所在直线为y轴.于是可以确定，点A的坐标为（0，2），点C的坐标为（3，0），D的坐标为（1，2）.如图4所示.

对于问题2，设P点的坐标为（0，yp），显然yp≥0.由于PCQD是平行四边形，因此H为CD、PQ的中点.C、D的坐标已知，因此H点的坐标为（2，1），故Q点的坐标为（4，2-yp），因此当yp=1时PQmin=4，此时P点的坐标为（0，1），PQ与AB垂直.

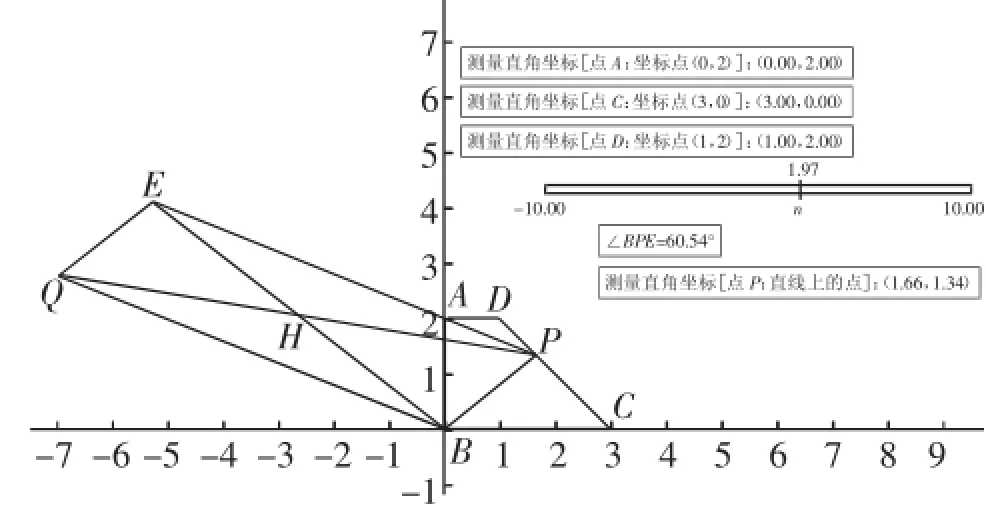
图6

通过上面的分析可以看出，在题目条件下，虽然点Q的位置随着点P的运动发生变化，但始终在直线x=4上，纵坐标的范围为［0，2］.

问题3的思路与方法与问题2一脉相承，只是细节处理略有不同.仍设P点的坐标为（0，yp），显然yp≥0.易得E（2，4-yp）.设PE、PC交于点H.则H）、Q（5，4-2y）p.于是当yp=时PQmin=5，此时P点的坐标为P Q与AB垂直.同样可以得出这样的结论：当点P在AB上运动时，点Q始终在直线x=5上，纵坐标的范围是［0，4］.

问题4在问题2、3的基础上又有所变化，点P的位置移到了直角梯形的非直角腰上，而且又多了一个变量n，如图5.通过观察计算，可以发现当P点由D到C的运动过程中，PQ逐渐变大，因此当P点与D点重合时，PQ最小.此时P点的坐标为（1，2），于是E（-n，2）1，0），所以

需要说明的是，网络上对于问题4的解析，一般认为当PQ与CD垂直时，PQ取得最小值（n+4），这样的结论是基于问题2、3的结论作出的判断.但是实际上，PQ取得最小值时PQ与CD并不垂直.

三、探讨

朱桂凤老师在文1中，认为这个题目的命制具有这样四个方面的突出特点：（1）知识点常见，易懂、易上手；（2）基于过程又高于过程；（3）解答方法需要融会贯通；（4）立意高远.本文完全赞同朱老师的看法，但同时也认为本题的命题立意可能不止于此.

1.从学生层面上看：增强了发现、分析数学问题的能力.

《义务教育数学课程标准2011年版》（以下简称《课标（2011）》）对数学课程内容的教材设计设定了“问题情境—建立模型—求解验证”的过程，问题情境是数学问题探究的起点.对于情境问题，依照《课标（2011）》的表述，不仅可以来源于现实社会、日常生活和其他学科的学习，还可以来源于数学知识内部本身.连云港市2012年中考第27题就是很好的问题来源，可以作为学生探究的数学情境.

在问题2、问题3的探究中，学生容易发现平行四边形对角线的交点H实际上是不动点，它完全由点C、点D确定，同样也可以由点P、点Q确定；换言之，由已知点C、点D确定的CD的中点H，可以用来确定点P或点Q，当点P的坐标通过假设的方式确定后，就可以通过这个中点H建立起点Q与点P之间的联系，从而确定PQ的长度.下面的问题就是要找到线段CD的中点H与线段端点C、D之间的关系了.随着坐标系的建立，这个关系学生容易发现.

数学问题从来不以得到正确解答为最终目的，而是要寻找解决的最佳途径.学生对于复杂几何图形的观察与思考产生了倦怠，产生了寻求更新的、更有效的解决办法的根本需要，这就是数学问题提出的动机之一.坐标系的建立使得数形结合思想得到充分发挥，通过分析找出问题解答的关键节点；对于这个关键节点，学生容易发现基于现有数学知识方法可以轻松解决，整个问题一下子豁然开朗了.在对问题的分析过程中，学生解构了原有的知识体系，并重新建构了一个新的体系基础，使得对问题的分析过程成为了一个“再发现”的过程.

因此我们有理由相信，本题命题的立意绝不仅仅是以加大难度而提升区分度，而是让这道初中数学的“最后一题”成为高中数学学习的大情境，提醒学生：随着年级段的跨越，将在数学学习中体会到更多、更深刻的数学思想方法，经历更多的知识体系的解构—建构过程，也会有更多的再发现.

2.从教师层面上看：基于初中而高于初中的另一种视界.

本文对题目的探究过程，用到了解析几何中最为基础的中点坐标公式、两点间距离公式，这是高中数学必修的内容，似乎与初中内容并无关联，对初中数学教学也没有更大的意义.但是，张奠宙先生“当用平面几何的方法难以解答时，可以尝试用解析几何的方法去理解和思考”的观点，一语道破天机，从数学思想方法和数学活动经验上打破了初高中之间的藩篱.

作为初中数学教师，我们给初中生讲授初中的数学知识、方法，但是我们绝不能囿于初中范围，更不能因为我们的自我隔离使学生的数学思维只能在初中范围内打转.我们不能也没必要在初中引入高中数学的内容来获得问题的解决，但是也不能使学生认为目前他们使用的方法是解决问题的唯一正确的途径.因此，从这个意义上来说，本题的命题者也是希望通过本题树立一个导向，希望教师在本题的探究过程中，开阔眼界，指导和帮助学生架好通往高中数学的桥梁.

3.从选拔的层面上看：数学思想方法的一种新提升.

本题作为中考试卷压轴题，担负着对考生进行选拔的重要责任，这一点朱桂凤老师在其文章中有所论述，此处不再赘述.我们想要说的是，中考试题对学生进行选拔之后是不是就没有其他的作用了呢？不是！选拔的作用是使得优秀的学生能够进入高一级的学校继续学习，而解析几何的思想方法又是高一级学校数学的必修内容.因此在选拔的同时又得以让学生管窥高中数学对同一数学内容处理的思想方法，更凸显了本题更高的命题立意.

“数”和“形”是数学中两个最基本的概念，数形结合又是最基本、最重要的数学思想方法.数形结合需要将几何直观和数量关系作为互相补充又相互转化的两方面，打通形象思维与抽象思维之间的关系.初中的几何内容基本上是经典的平面几何内容，有着数千年的历史渊源，更偏重于对“形”的观察与思考，对于学生学会对问题进行逻辑推理至关重要.但是，我们不能只停留在这一层面上.经典平面几何确实滋润了无数代人，这些人中有普通人也有杰出的科学家、数学家，而在此基础上发展起来的解析几何则更好地打通了“数”和“形”之间的联系，其思想方法有着更为广泛的应用空间.在初中数学中，我们经常把函数作为数形结合在初中数学中的典范内容，以“数”定“形”：先研究函数的解析式，再通过解析式研究函数的图像和性质，而这只是数形结合的一个方面.数形结合的另一个方面是以“形”定“数”，即对每一个几何对象，通过引入坐标，研究几何对象间的数量和位置关系，在初中数学中研究较少.因此，命题者也是想通过本题告诉全体初中数学教师和学生，对于数形结合思想乃至全部的数学思想方法的理解，不能因为知识层次的分别而局限于某一方面；数学知识、技巧、方法因时不同，但是数学思想方法是灵魂，贯穿始终.

综上所述，连云港市2012年中考第27题的命题者试图以数学中最基本、最重要的数形结合思想方法为纽带，破除初高中数学的壁垒，力图将初中数学学习的经验作为高中数学学习的奠基.同时，命题者也借本题提醒初中数学教师对《课标（2011）》中新增添的“基本思想”和“基本活动经验”、“两能”必须予以足够的重视，并以“终极”案例的形式指明了对“四基”“两能”的培养方向.

1.朱桂凤.一道简约的动点性最值问题新考［J］.中国数学教育，2013（7/8）.

2.李铁安主编.义务教育课程标准（2011年版）案例式解读（初中数学）［M］.北京：教育科学出版社，2012.

3.史宁中主编.义务教育数学课程标准（2011年版）解读［M］.北京：北京师范大学出版社，2012年.

4.［美］R·柯朗，著.左平，译.什么是数学——对思想和方法的基本研究（增订本）［M］.上海：复旦大学出版社，2008.

5.邵长亮.以数学写作推进数学尚“识”教育［J］.中学数学（下），2014（12）.