深入研究揭示结构，归类复习变式再练——以“曲线压轴题”为例

☉江苏苏州工业园区金鸡湖学校沈奕

深入研究揭示结构，归类复习变式再练
——以“曲线压轴题”为例

☉江苏苏州工业园区金鸡湖学校沈奕

中考压轴题常常与函数图像相关，而且以抛物线居多，曲线（反比例函数图像）的相对较少，然而曲线压轴难题往往难以破解，容易走偏求解方向，导致思路受阻.在中考二轮备考期间，加强曲线压轴题的备考研讨很有必要.本文结合一道曲线压轴题，破解思路，并跟进教学思考，供研讨.

一、模考题及思路突破

模考题：如图1，正方形OABC的边长为2，点A、C分别在x轴、y轴的正半轴上，曲线L：y=（x＞0）与BC、AB分别交于点D、E，且BD=AE.

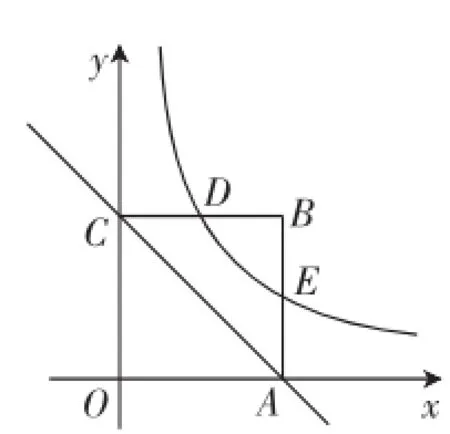
图1

（1）求k的值.

（2）若点P在直线AC上，且四边形BCPQ是菱形，求证点Q在曲线L上.

（3）点F在线段AC上，且不与点A、C及AC的中点重合，过点F作x轴的垂线，交曲线L于点M，过点F作y轴的垂线，分别交曲线L、AB于点N、G，连接MN、BN.试判断∠BNG与∠FMN之间的数量关系，并说明理由.

思路简述：（1）由正方形OABC的边长为2，可得点B的坐标为（2，2），设DAE=.结合BD=AE，列出方程2-=，解得k=2.

（2）由A（2，0）、C（0，2）得直线AC的方程为y=-x+2.由四边形BCPQ为菱形，得PQ平行且等于BC，PQ=PC=2.接下来要分两种可能情况分类讨论：

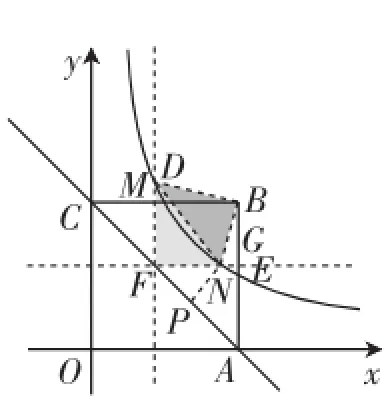
图2

综上可知：点Q在曲线L上.

（3）先构造可能的图形分析，如图2：

分两种情况讨论：

①当点F在AC的中点和点C之间时，连接BM.设点N（m，n），则F（-n+2，n），FN=m+n-2，根据勾股定理可得BN2=（2-m）2+（2-n）2=8-4（m+n）+m2+n2.对该式子配出一个2mn后可以写成完全平方式，而2mn又是一个常数4，整理、配方得BN2=（m+n-2）2.而FN=m-（-n+2）=m+n-2.即证得BN= FN.同样，可演算出BM=FM.又MN=MN，所以△BMN≌△FMN.所以∠MBN=∠MFN=90°，∠BMN=∠FMN.即∠BNG=∠BMF=2∠FMN.

②当点F在AC的中点与点A之间时，同理可得∠BNG+ 2∠FMN=180°.

综上可得：∠BNG=2∠FMN或∠BNG+2∠FMN= 180°.

解后反思：在图2中，容易发现B、M、F、N四点共圆（以MN为直径的圆），从四点共圆的角度来理解∠BNG与∠FMN之间的数量关系，可获得更深刻的理解.

此外，该题将反比例函数图像的焦点、准线以这种方式呈现出来，非常巧妙！当然，初中对反比例函数图像的焦点、准线没有要求.

二、关于曲线压轴题的教学研讨

1.反比例函数的图像性质简约、深刻，值得深入探究.

教材上关于反比例函数的图像性质认识比较初步，比如，函数增减性，或从反比例函数图像上任意一点向两坐标轴引垂线段，与坐标轴所围成的矩形的面积是定值.事实上，近年来各地中考对反比例函数的性质探究得比较深入，比如，图3中，点A、B在反比例函数图像上，过点A、B分别作x、y轴的垂线段AA′、BB′，则一定有AB∥A′B′.

重要的是，该性质还可拓展、生长，比如，不管两个点的位置在同一支曲线上还是分别在两支上，该结论始终成立（如图4~6）.

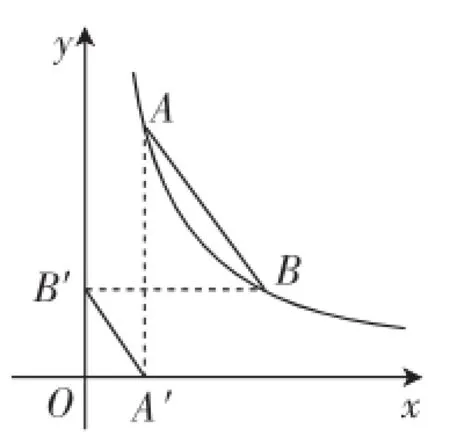
图3

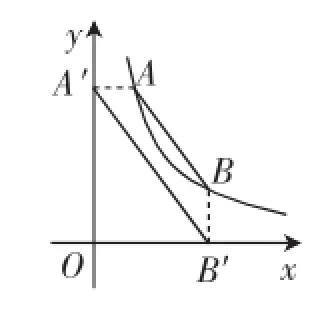
图4

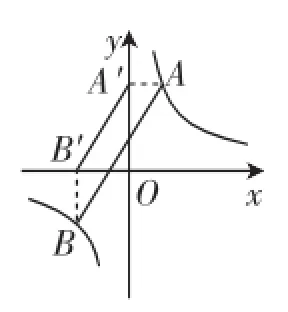
图5

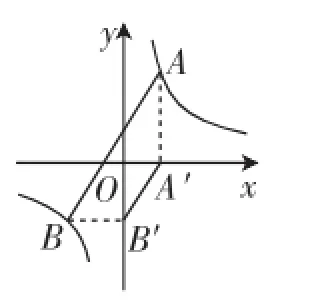
图6

进一步，如图7，作直线AB交x、y轴于N、M，会有平行四边形AMB′A′、平行四边形A′B′BN.从而可得AM=BN.将图7中的相关线段删减后，又可得出图8所示的两个阴影三角形，容易发现△AOM与△BON的面积一定相等！

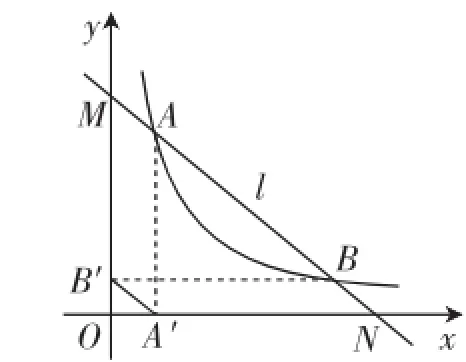
图7

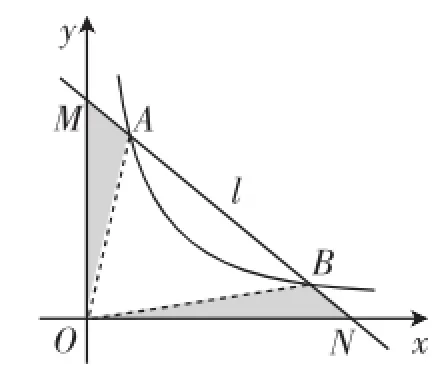
图8

而在上文中，隐含了反比例函数图像的焦点与准线，如果不熟悉该题结构，则会在黑暗中摸索，消耗考场上宝贵的时间.

2.曲线压轴题要注意引导学生排除干扰，分离并识别模型.

曲线压轴题一般都有3个小问，为了能化解难点，通常第一问都是简单问题，第二问会渐次展开探究，需要一定的解题能力，但贯通思路往往也不难，第三问却会向深处拓展，有较高的解题要求.比如，上文中的考题第三问，需要学生自己构出图2进行分析，并且要恰当设元，如果设元不当，则会陷入繁杂的运算，有可能不能演算出正确的结论.待到我们分析出解题的思路之后，就能得到关于曲线焦点的奇异性质，感受到命题者把一道曲线难题经过精心的伪装，结合初中阶段的正方形、曲线呈现出来，而把曲线的准线用正方形的对角线隐藏起来，把正方形一个顶点作为焦点隐藏起来，这样在讲评时，就要注意引导学生在演算出相关线段相等之后，反思结构、走向一般，对于特别优秀的学生，可建议他们回去钻研曲线更多的奇妙性质.

3.曲线压轴题教学要注意适当归类，专题聚焦重点突破.

曲线压轴题考查方向多样，如果仅仅把看似以曲线为载体的压轴题集中在一起讲解，效果并不是最优的，因为同样两道看似相同的曲线压轴题，很可能它们的求解方向、解题策略截然不同.这就要求我们从试题本质、结构、求解方向的高度来组织同类压轴题，甚至有时不仅可把综合题组合在一起，也可以从填空、选择题中归类组合，形成专题，引导学生围绕一类问题聚焦，重点突破，让学生通过具有共同结构的一类曲线问题的训练，达到较好的训练效果，增加“眼力”，下次再碰到具有类似结构的曲线问题，能一眼看出问题结构与求解方向.

4.曲线压轴题讲评之后要对难点问题展开变式再练.

近两年《中学数学（下）》刊出的不少文章都倡导解题教学要重视开展听课检测、变式再练，这是非常重要的解题教学环节.我们也对上面的考题进行变式改编，作为讲评之后的变式反馈题：

模考题变式再练：如图1，正方形OABC的边长为2，点A、C分别在x轴、y轴的正半轴上，曲线L：y=k x（x＞0）与BC、AB分别交于点D、E.

（1）当D为边BC的中点时，求点E的坐标.

（2）在（1）的条件下，若点Q在曲线L上，当四边形BCPQ是菱形时，求点P的坐标.

（3）点F在线段AC上，且不与点A、C及AC的中点重合，过点F作x轴的垂线，交曲线L于点M，过点F作y轴的垂线，分别交曲线L、AB于点N、G，连接MN，BN.

【说明，以下两个小问题，只要选择一个小问解答即可】

①小宇经过演算发现：∠BNG=2∠FMN.请判断“小宇发现”的真假，并说明理由.

②小凡经过推理发现：B、M、N、F四点共圆.请判断“小凡发现”的真假，并说明理由.

1.章建跃.创新推动改革，全面提高教育质量——暨“第九届初中青年数学教师优秀课展示与培训活动”总结［J］.中国数学教育（初中），2016（4）.

2.郑毓信.“开放的数学教学”新探［J］.中学数学月刊，2007（7）.

3.郑毓信.多元表征与概念教学［J］.小学数学教育，2011（10）.

4.宋秀云.让“简单内容”教得深刻［J］.数学通报，2016，55（4）.