基于微分同胚优化极端学习机的人脸识别
2017-04-24李丽娜闫德勤楚永贺
李丽娜 闫德勤 楚永贺
(辽宁师范大学计算机与信息技术学院 辽宁 大连 116081)
基于微分同胚优化极端学习机的人脸识别
李丽娜 闫德勤 楚永贺
(辽宁师范大学计算机与信息技术学院 辽宁 大连 116081)
极端学习机(ELM)以其快速高效和良好的泛化能力在模式识别领域得到了广泛应用。然而当前的ELM及其改进算法并没有充分考虑到隐层节点输出矩阵对极端学习机泛化能力的影响。通过实验发现激活函数选取不当及数据维数过高将导致隐层节点输出值趋于零,使得输出权值矩阵求解不准,降低ELM的分类性能。为此,提出一种微分同胚优化的极端学习机算法。该算法结合降维和微分同胚技术提高激活函数的鲁棒性,克服隐层节点输出值趋于零的问题。为验证所提算法的有效性使用人脸数据进行实验。实验结果表明所提算法具有良好的泛化性能。
极端学习机 激活函数 微分同胚
0 引 言
近来Huang等人[1-3]基于单隐层前馈神经网络SLFNs结构提出了一种极端学习机ELM算法[4]。与现有的神经网络算法相比,ELM随机产生隐层节点的输入权值和偏置值,在所有的参数中仅有输出权值是经过分析确定,通过平方损失误差函数将求解输出权值转化为最小二乘解问题。文献[5-7]通过分析指出ELM在随机产生隐层节点的输入权值和偏置值,分析确定输出权值保持了SLFNs的通用逼近能力。与基于梯度思想的方法相比,ELM具有更高的效率和更好的泛化能力[8-10],与支持向量机SVM的二次规划问题相比ELM采用最小二乘解具有非常快的求解速度。实际的研究中已经证实ELM与SVM及其改进相比具有更好的泛化能力[11-12]。在过去的十几年里ELM在理论和应用方面都得到了长足的发展,文献[13]进一步证实了ELM的通用逼近能力。文献[14]在统计学习理论框架下进一步探究了ELM的泛化能力,对于具体问题的特殊需求已在ELM算法的基础上提出了各种改进,例如将ELM应用于在线连续数据学习[15-17]、不平衡数据学习[18]、噪音及缺失数据[19-20]和人脸识别[21]问题等。除了ELM可以应用到传统的回归和分类问题中,近年来研究者已将ELM应用于聚类[22]、特征提取[23]和表征学习中[24]。
虽然ELM在模式识别和机器学习领域得到了广泛的应用,但该算法并没有充分考虑到隐层节点输出矩阵对极端学习机分类性能和泛化能力的影响,文献[25]通过分析指出,当隐层节点输出矩阵存在不适定问题时(隐层节点输出值包含非常多的零元素),将导致输出权值矩阵求解不准,造成过拟合的现象,从而影响ELM的分类性能和泛化能力。隐层节点输出矩阵存在不适定问题的主要原因是由于激活函数选取不当及数据样本维数过高。通过实验发现数据样本维数较高时,若利用Sigmoid函数和高斯函数作为激活函数处理人脸数据,隐层节点输出矩阵将会包含非常多接近零的元素,导致输出权值矩阵求解不准,降低ELM的分类性能和泛化能力。为了解决激活函数导致隐层节点输出矩阵的病态问题,本文在Sigmoid函数的基础上提出一种微分同胚优化及鲁棒激活函数DRAF(Diffeomorphic optimized robust activation function)的极端学习机算法(简称为DRAFELM)。该算法结合微分同胚技术提高激活函数的鲁棒性,利用降维技术消除数据样本包含的冗余属性对激活函数的影响,同时利用微分同胚优化激活函数有效避免隐层节点输出矩阵存在不适定问题;利用改进的降维方法获取数据的局部和全局信息,进而提高ELM的泛化能力。
本文所提的算法改进包括:
(1) 所提出的激活函数(DRAF)将Sigmoid激活函数中的输入权值及隐层节点偏置值与数据样本间的计算关系转化为余弦度量,进而将这种余弦度量关系映射到微分同胚空间。微分同胚空间能够很好地保持数据样本之间的内在流形特征,有效避免数据样本维数过高以及数据样本含有的噪音和离群点对Sigmoid激活函数的影响,提高ELM的泛化性能。
(2) 提出一种有监督稀疏排列的局部保持投影降维算法SSLPP(surprised sparse locality preserving projections)。SSLPP通过计算数据的邻域信息动态确定数据局部线性化邻域范围,准确获取数据的全局和局部的判别信息。该方法克服了传统降维算法对数据样本学习不充分的问题,能有效消除数据样本包含的冗余属性对激活函数的影响,进而可以有效避免隐层节点输出矩阵的不适定问题。
为验证所提算法的有效性,实验使用Yale、Yale B、ORL、UMIST人脸数据,结果表明本文的改进算法能够显著提高ELM的分类性能和泛化能力。
1 激活函数相关问题分析
文献[26]指出非线性分段连续函数作为激活函数常用的有以下几种。
(1) Sigmoid函数:
(1)
(2) Hard-limit函数:
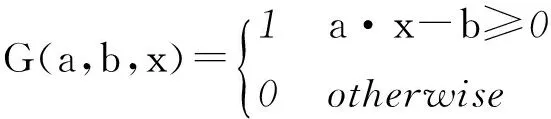
(2)
(3) Gaussian函数:
G(a,b,x)=exp(-b‖x-a‖2)
(3)
由式(1)-式(3)可知,上述三种激活函数的界为[0,1],对于任意数据样本x不可避免地出现隐层节点输出值为零的情况,只有当数据分布近似满足所选定的激活函数分布时,ELM应用相应的激活函数才能够取得良好的效果;反之,激活函数的输出值会非常小,即隐层节点输出矩阵含有很多接近零的元素,当数据样本维数过高时上述情况将会更加严重。
由以上分析可知Sigmoid函数、Hard-limit函数、Gaussian函数都有可能使隐层矩阵输出值为零,下面通过例子说明上述情况。
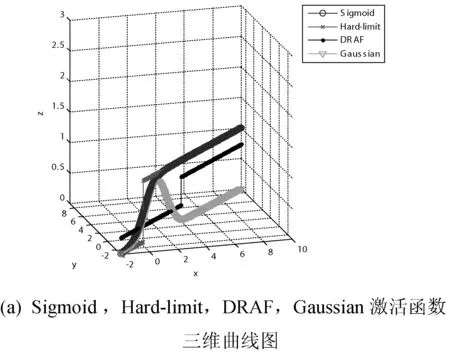
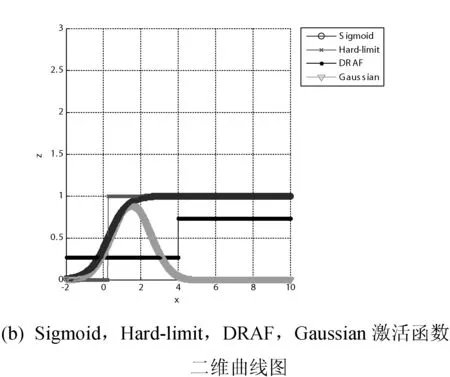
图1 样本A在激活函数下的输出值分布
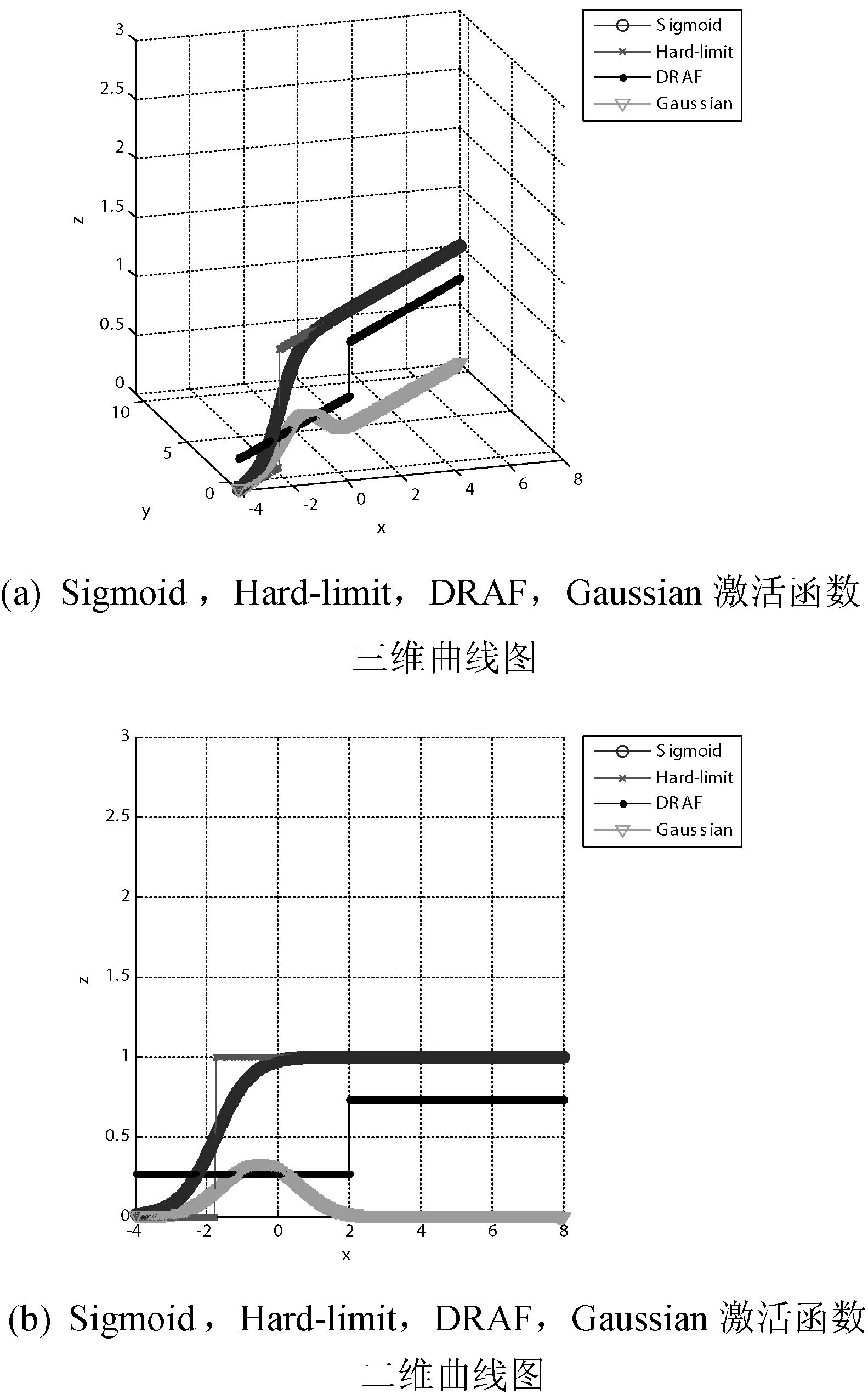
图2 样本B在激活函数下的输出值分布
由图1和图2可以看出对于均匀分布的数据样本A和B,Sigmoid函数、Hard-limit函数、Gaussian函数都在不同程度上出现了激活函数输出值为零的情况,由图中(b)可以看出上述情况更加严重,这将会导致隐层节点输出矩阵出现病态问题,从而使输出权值过大,出现过拟合学习。DRAF的值维持在(0.2,0.75),很好地避免了隐层节点输出矩阵出现病态问题。
2 ELM及微分同胚优化及鲁棒激活函数的极端学习机(DRAFELM)
2.1ELM基本概念
对于N个不同的样本(xj,tj),可表示为X=(x1,x2,…,xN)T∈RD×N,其中tj=(tj1,tj2,…,tjm)T∈Rm,具有L个隐层节点激活函数为g(x)的ELM模型如下形式:
(4)
其中j=1,2,…,N,ai=(ai1,ai2,…,ain)为连接第i个隐层节点与输入节点的输入权值向量,βi=(βi1,βi2,…,βim)为连接第i个隐层节点与输出节点的输出权值向量,bi为第i个隐层节点的偏置值,ai·xj表示ai和xj的内积,tj=(tj1,tj2,…,tjm)T∈Rm为对应于样本xj的期望输出向量,对所有数据样本进行整合,式(4)可以改写为如下形式:
Hβ=T
(5)
其中H是网络隐层节点输出矩阵,β为输出权值矩阵,T为期望输出矩阵:
(6)
(7)
当隐层节点个数和训练样本个数相同时(即L=N)我们可以通过式(5)直接求矩阵H的逆矩阵得到最优的输出权值矩阵β,但大多情况下隐层节点的个数远小于训练样本的个数,此时矩阵H为奇异矩阵,我们利用最小二乘解的方法对式(5)进行求解:
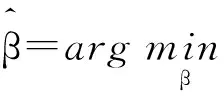
(8)
其中H+为矩阵H的广义逆。
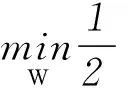
(9)
式中,ξi=(ξi1,…,ξ1m)T为对应于样本xi的训练误差向量,C为惩罚参数。式(9)的求解可通过拉格朗日方法转化为无条件最优化问题进行求解。因此ELM算法求解过程可总结步骤如下:
(1) 初始化训练样本集;
(2) 随机指定网络输入权值a和偏置值b;
(3) 通过激活函数计算隐层节点输出矩阵H;
2.2 微分同胚优化及鲁棒激活函数的极端学习机(DRAFELM)
及时清除温室内病虫害的叶片、果实,减少病虫害发生的污染源,并将之深埋或烧毁。同时对相应区域及时灭菌与消毒,主要包含棚架、栽培器材以及土壤等。
2.2.1DRAF的提出
为了使激活函数对数据样本维数过高及噪音具有更强的抗干扰能力,避免隐层节点输出矩阵输出值为零,提高ELM的泛化性能,本文在Sigmoid的基础上提出一种基于微分同胚思想的鲁棒激活函数(DRAF)。
微分同胚[27]是建立在李群上的一个空间。李群空间具有光滑流形和群的特点。李群与李代数具有对应关系。李代数是一种代数结构,李群在单位元e处的切空间是李代数的向量空间。李群在单位元附近的局部性状由李代数刻画,在指数映射作用下可以将李代数的性质提升到李群的层次。指数映射exp(·)是一个从李代数g中0的邻域到李群G中单位元e的邻域的微分同胚。设e1,e2,…,en是单位元e处切空间D(G)的一组基在局部坐标系中对t∈G邻域中的任意元素x,存在一个切空间的向量μ=∑iμiei∈De(G),使得x=t·exp(μ)。于是李群G上某一光滑函数在x处的泰勒展开式为:
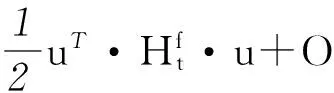
(10)
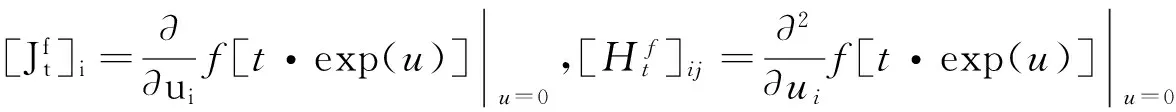
微分同胚将隐层节点输出矩阵映射到同胚空间能够很好地保持数据的流形信息,因此基于微分同胚思想的鲁棒激活函数形式如下:
temph=ax+b
(11)
(a为输入权值,b为隐层节点偏置值,x为输入样本)
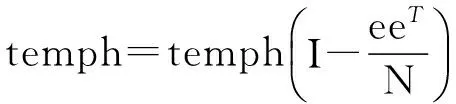
(12)
将I代入式(10)可得:
f(I) =f[t·exp(u)]
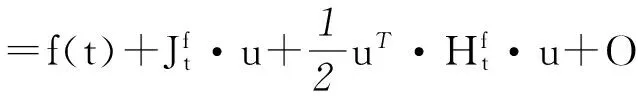
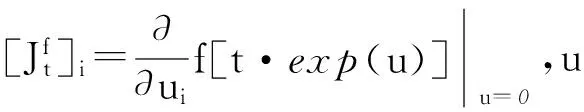
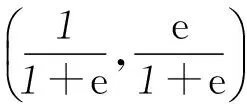
2.2.2 构造新的降维算法
现实中很多数据样本具有较高的维数,高维数据包含的冗余属性减弱了激活函数的鲁棒性,从而导致隐层节点输出矩阵的不适定问题。为此,本文提出一种有监督稀疏排列的局部保持投影降维算法。
对于稀疏的人脸图像数据样本集,样本间重叠的信息量非常少,若利用传统降维算法学习稀疏样本集,则会导致欠学习的现象。为此,通过扩大k邻域为k-N(i)区域对原始数据集进行区域信息加强,如图3所示,k-N(xi)区域为N(xi)及其对应的k近邻点构成,这使得在数据样本集较少的情况下,同样能够实现重叠信息量非常充分的流形学习效果,进而实现流形学习算法对人脸图像数据判别信息的有效提取。通过全局优化的方法对N(xi)及其对应的k近邻点构成的信息域进行优化。
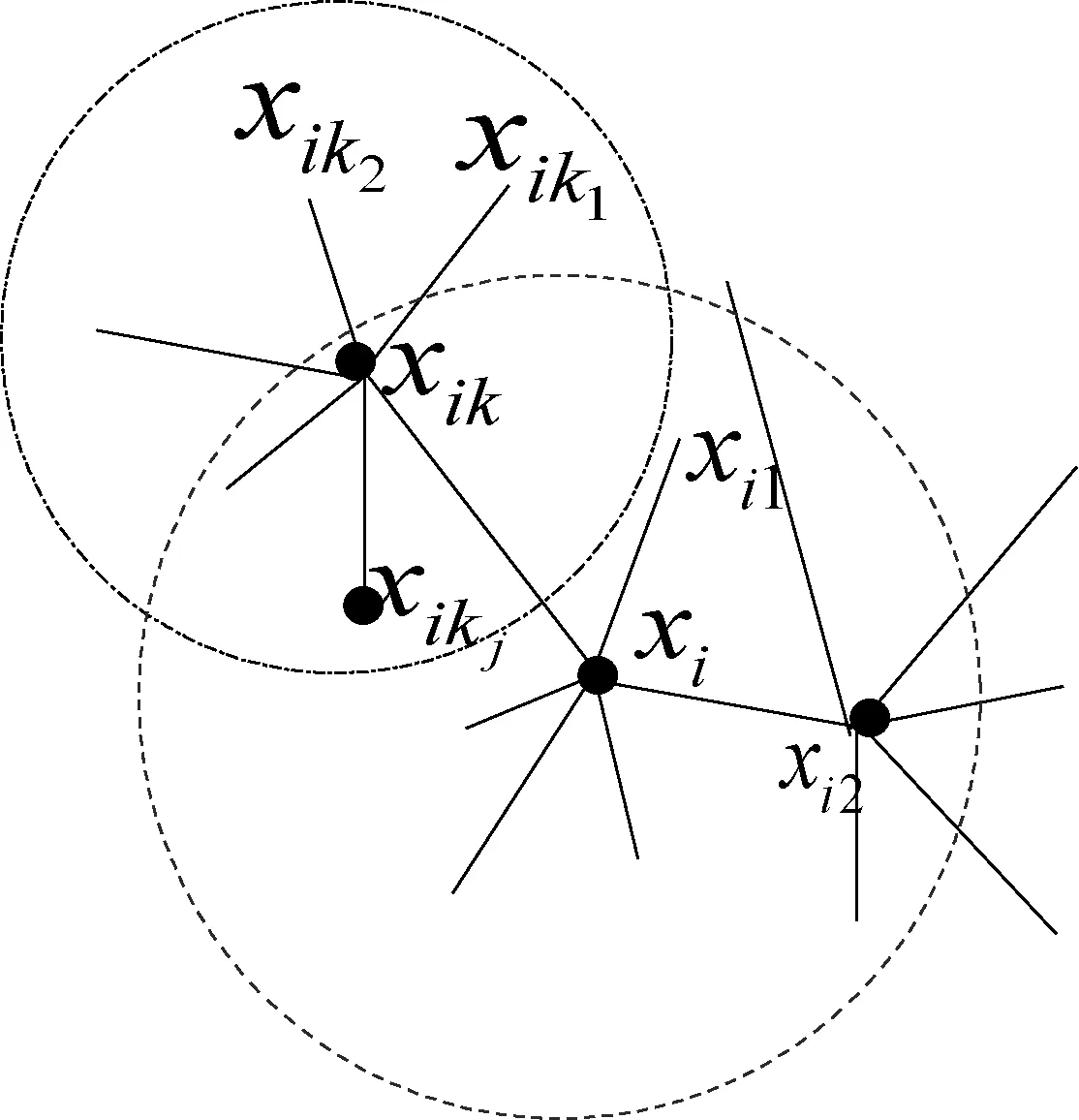
图3 以xi为中心的k-N(i)域
希望k-N(i)邻域降维后样本的邻域关系尽可能保持不变,则第i个样本邻域最小化目标函数为:
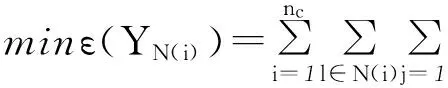
(13)
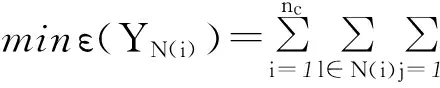
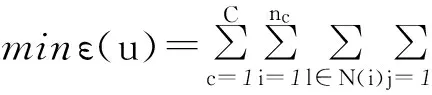
(14)
式中,c为所有样本的类别总数,uT为投影变换矩阵。依据文献[28]对局部保持投影算法LPP(localitypreservingprojection)推导过程,对式(14)进行整理得:
(15)
其中Yi=[yi1,…,yik],el=[1,…,1]T,Il∈Rl×l的单位矩阵,L为拉普拉斯矩阵。有监督稀疏排列的局部保持投影降维算法SSLPP(surprisedsparselocalitypreservingprojections)保持了LPP[29]算法原有的框架,因此优化条件可写为:
minε(u)=tr(uTXLXTu)s.t. uTXDXTu=I
(16)
其中Dii=∑jwij利用拉格朗日乘子法对式(16)进行求解可得:
XLXTu=λXDXTu
(17)
对矩阵XLXT和XDXT进行特征值分解,得到特征向量矩阵为U=[u1,u2,…,uN]。从特征向量矩阵中选取的第2到第d+1个最小特征值对应的特征向量,即:[u2,u3,…,ud+1]T,则由y=uTx得到SSLPP算法。
2.2.3DRAFELM算法
微分同胚优化及鲁棒激活函数的极端学习机DRAFELM算法的步骤如下:
(1) 初始化训练样本集,利用式(17)对数据集进行降维,得到数据集的低维表示Y;
(2) 随机指定网络输入权值a和偏置值b;
(3) 利用DRAF计算ELM的隐层输出矩阵H;
(4) 计算输出权值β。
3 实验结果及分析
为了验证本文方法的有效性,本文从两方面进行实验,一方面采用激活函数Gaussian,Sigmoid,Hard-limit,DRAF与三种降维算法SSLPP、PCA[30]、LPP[29]和LPANMM[31]结合在人脸数据集上进行对比实验,将本文提出的鲁棒激活函数DRAF与Gaussian、Sigmoid和Hard-limit函数进行对比,其次将本文提出的降维算法SSLPP与PCA、LPP和LPANMM进行对比。另一方面从ELM算法的角度,将本文提出的DRAFELM算法与ELM、MCVELM[32]、GELM[21](均采用激活函数Sigmoid)进行对比实验。为了实验的公平性,本次实验中四种不同ELM算法的隐层节点均设置为200,惩罚参数设置为C=25。所用电脑为惠普工作站,处理器:Intel(R)Xeon(R)CPUE5-1603 0 @2.80GHz,内存:8.00GB,操作系统:MicrosoftWindows7(64位)。所使用的不同人脸库图像如图4所示,4个不同人脸数据库在人脸识别实验中的参数设置如表1所示。

图4 不同人脸图像的训练集
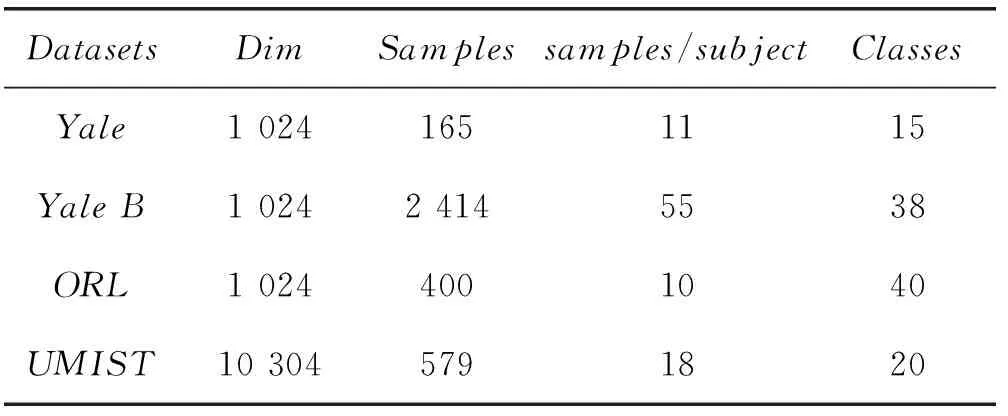
DatasetsDimSamplessamples/subjectClassesYale10241651115YaleB102424145538ORL10244001040UMIST103045791820
3.1 不同激活函数及不同降维算法的比较
本节中分别采用Sigmoid,Hard-limit,Gaussian,DRAF激活函数函数应用于3个不同人脸数据库,并且进一步对比了LPP,PCA及LPANMM与SSLPP降维算法降至不同维度的识别率,识别率曲线如图5-图7所示及识别率如表2所示。(实验中ELM算法的隐层节点个数设置为200,惩罚参数设置为C=25。训练集和测试集分别为总数据样本的1/2)。
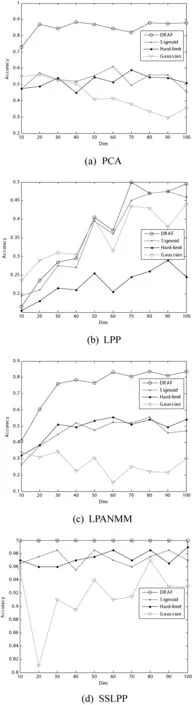
图5 ORL人脸数据识别率曲线
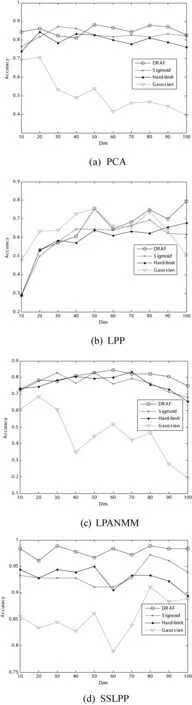
图6 UMIST人脸数据识别率曲线
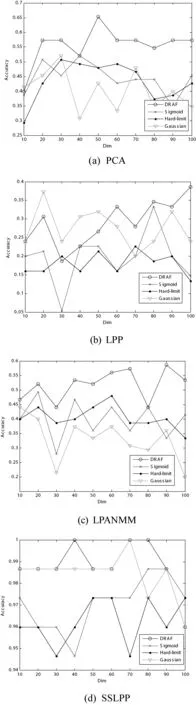
图7 Yale人脸数据识别率曲线
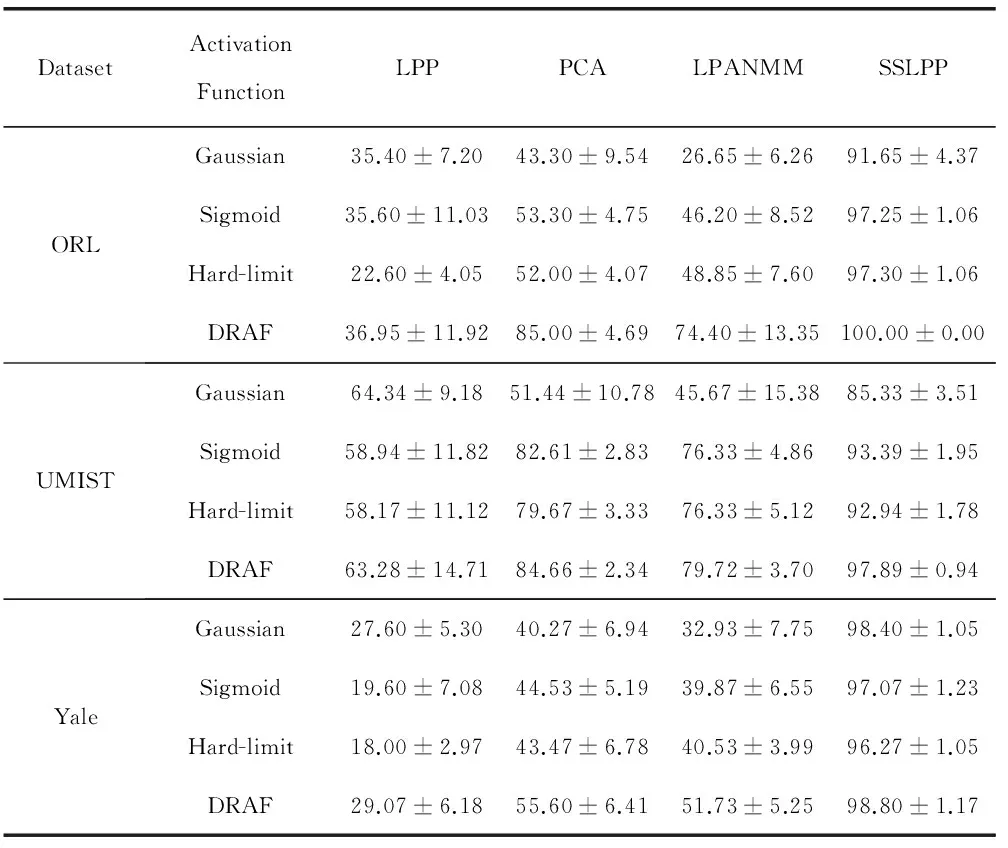
DatasetActivationFunctionLPPPCALPANMMSSLPPORLGaussian35.40±7.2043.30±9.5426.65±6.2691.65±4.37Sigmoid35.60±11.0353.30±4.7546.20±8.5297.25±1.06Hard-limit22.60±4.0552.00±4.0748.85±7.6097.30±1.06DRAF36.95±11.9285.00±4.6974.40±13.35100.00±0.00UMISTGaussian64.34±9.1851.44±10.7845.67±15.3885.33±3.51Sigmoid58.94±11.8282.61±2.8376.33±4.8693.39±1.95Hard-limit58.17±11.1279.67±3.3376.33±5.1292.94±1.78DRAF63.28±14.7184.66±2.3479.72±3.7097.89±0.94YaleGaussian27.60±5.3040.27±6.9432.93±7.7598.40±1.05Sigmoid19.60±7.0844.53±5.1939.87±6.5597.07±1.23Hard-limit18.00±2.9743.47±6.7840.53±3.9996.27±1.05DRAF29.07±6.1855.60±6.4151.73±5.2598.80±1.17
图5-图7给出了分别采用Gaussian、Sigmoid、Hard-limit和DRAF激活函数,与SSLPP、LPP、PCA和LPANMM三种降维算法结合在ORL、UMIST和Yale人脸数据集的识别率曲线。从激活函数角度由图5-图7可以看出DRAF的识别率曲线显著高于其他激活函数的识别率曲线,从而可以证实DRAF的鲁棒性。由图5-图7还可以看出Sigmoid和Hard-limit激活函数的识别率曲线比较接近,在PCA和LPANMM降维识别率曲线中可以看出随着数据维数的增大,Gaussian函数的识别率曲线出现下降的趋势,这也验证了对于维数过高的数据样本在激活函数选取不当的情况下导致隐层节点输出矩阵出现病态问题。从降维的角度,图5-图7可以看出本文所提降维算法的识别率曲线远高于LPP、PCA和LPANMM降维算法的识别率曲线。这主要是由于SSLPP通过计算人脸图像数据的邻域信息动态确定人脸图像数据局部线性化邻域范围,准确获取人脸图像数据的全局和局部的判别信息。因此,克服了传统降维算法对数据样本学习不充分的问题,有效消除数据样本包含的冗余属性对激活函数的影响,避免了隐层节点输出矩阵的不适定问题,从而提高了ELM的分类性能和泛化性能。表2给出了ORL、UMIST和Yale人脸数据集的识别率,从表2可以看出DRAF的识别率普遍高于其他激活函数的识别率并且SSLPP的识别率高于PCA和LPANMM降维算法的识别率。
3.2 DRAFELM与ELM及其改进算法比较
实验将DRAFELM与ELM、MCVELM[32]和GELM[21]进行对比。ELM、MCVELM和GELM均采用Sigmoid函数作为激活函数,实验使用Yale、Yale B、ORL和UMIST人脸数据,实验结果如图8及表3所示(为了实验的公平性,实验中不同ELM算法的隐层节点个数设置为200,惩罚参数设置为C=25,图8中TrainNum表示训练样本个数)。
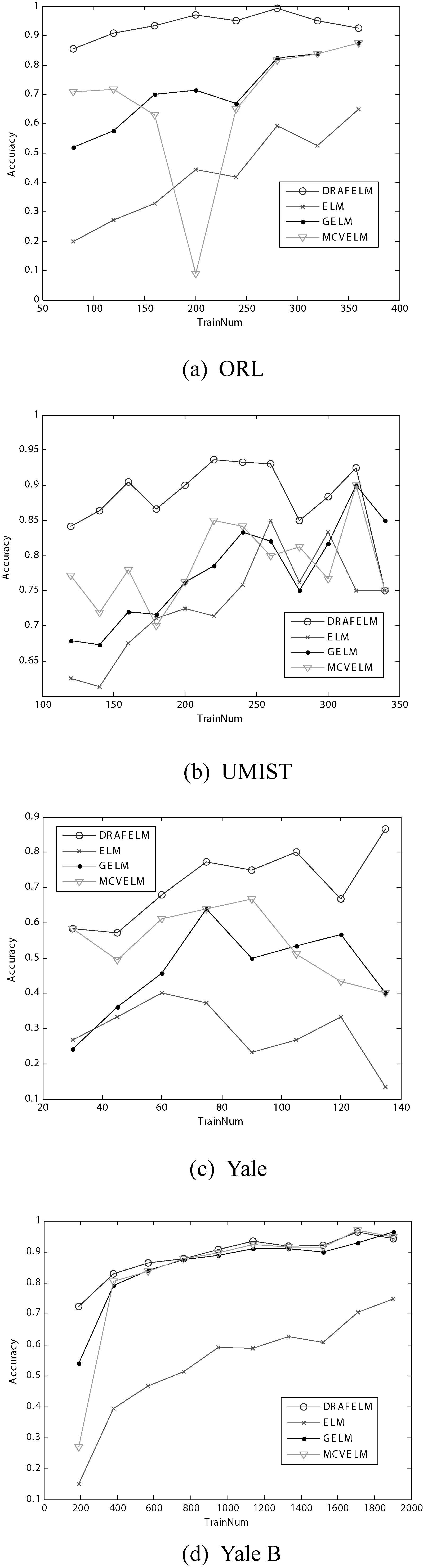
图8 ELM,MCVELM,GELM, DRAFELM识别率曲线
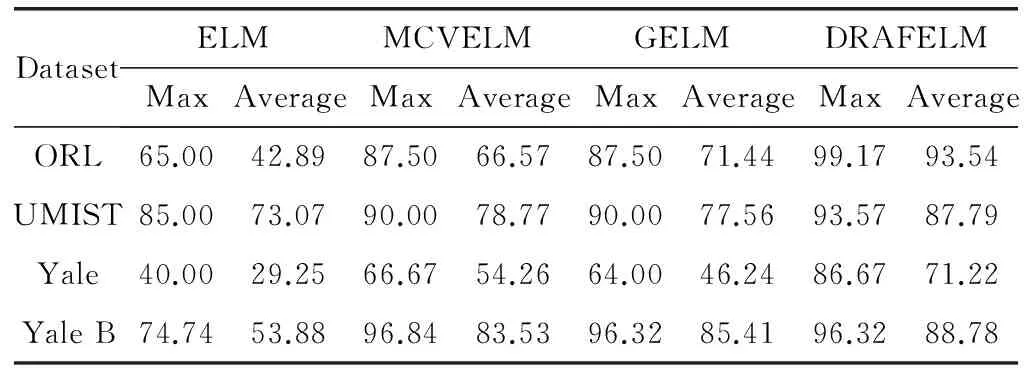
DatasetELMMCVELMGELMDRAFELMMaxAverageMaxAverageMaxAverageMaxAverageORL65.0042.8987.5066.5787.5071.4499.1793.54UMIST85.0073.0790.0078.7790.0077.5693.5787.79Yale40.0029.2566.6754.2664.0046.2486.6771.22YaleB74.7453.8896.8483.5396.3285.4196.3288.78
图8和表3给出了ELM及其改进算法在ORL、UMIST、Yale和Yale B人脸数据集的识别率曲线及识别率,从图8和表3可以看出DRAFELM的识别率显著高于其他算法的识别率,进一步验证了本文算法DRAFELM的鲁棒性。
4 结 语
为了有效避免隐层节点输出矩阵的病态问题,本文提出一种微分同胚优化的鲁棒激活函数的极端学习机算法。本文的创新是考虑到当激活函数选取不当及数据样本维数过高将导致隐层节点输出值趋于零,使得输出权值矩阵求解不准,造成过拟合的现象,因此在Sigmoid函数的基础上提出一种微分同胚优化的鲁棒激活函数。DRAF将Sigmoid激活函数中的输入权值及隐层节点偏置值与数据样本间的计算关系转化为余弦度量,进而将这种余弦度量关系映射到微分同胚空间。为了解决数据样本维数过高将导致隐层节点输出值趋于零的问题,提出一种有监督稀疏排列的局部保持投影降维算法。通过计算数据的邻域信息动态确定数据局部线性化邻域范围,准确获取人脸图像数据的全局和局部的判别信息。通过实验结果表明,本文所提出的方法显著提高了极端学习机的分类性能和泛化能力并且优于其他算法。
[1] Feng G,Huang G B,Lin Q.Error minimized extreme learning machine with growth of hidden nodes and incremental learning[J].IEEE Transactions on Neural Networks,2009,20(8):1352-1357.
[2] Tang J,Deng C,Huang G B.Extreme learning machine for multilayer perceptron[J].IEEE Transactions on Neural Networks and Learning Systems,2015(99):1-13.
[3] Huang G B,Zhou H M,Ding X J,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2012,42(2):513-529.
[4] Rajesh R,Prakash J S.Extreme learning machines-A Review and State-of-the-art[J].International Journal of Wisdom based Computing,2011,1:35-49.
[5] Huang G B,Chen L,Siew C K.Universal approximation using incremental constructive feedforward networks with random hidden nodes[J].IEEE Trans.Neural Netw.,2006,17(4):879-892.
[6] Huang G B,Chen Y Q,Babri H A.Classification ability of single hidden layer feedforward neural networks[J].IEEE Trans.Neural Netw.,2000,11(3):799-801.
[7] Zhang R,Lan Y,Huang G B,et al.Universal approximation of extreme learning machine with adaptive growth of hidden nodes[J].IEEE Trans.Neural Netw.Learn.Syst.,2012,23(2):365-371.
[8] Wang Y,Cao F,Yuan Y.A study on effectiveness of extreme learning machine[J].Neurocomputing,2011,74(16):2483-2490.
[9] Wang X,Chen A,Feng H.Upper integral network with extreme learning mechanism[J].Neurocomputing,2011,74(16):2520-2525.
[10] Shi L C,Lu B L.EEG-based vigilance estimation using extreme learning machines[J].Neurocomputing,2013,102:135-143.
[11] FernándezDelgado M,Cernadas E,Barro S,et al.Direct kernel perceptron (DKP):Ultra-fast kernel ELM-based classification with noniterative closed-form weight calculation[J].Neural Networks,2014,50:60-71.
[12] Huang G,Song S J.Semi-supervised and unsupervised extreme learning machines[J].IEEE Transactions on Cybernetics,2014,44(12):2405-2417.
[13] Huang G B,Zhou H M,Ding X J,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2012,42(2):513-529.
[14] Liu X Y,Gao C H,Li P.A comparative analysis of support vector machines and extreme learning machines[J].Neural Netw.,2012,33:58-66.
[15] Zhao J W,Wang Z H,Park D S.Online sequential extreme learning machine with forgetting mechanism[J].Neurocomputing,2012,87:79-89.
[16] Rong H J,Huang G B,Sundararajan N,et al.Online sequential fuzzy extreme learning machine for function approximation and classification problems[J].IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics,2009,39(4):1067-1072.
[17] Liang N Y,Huang G B,Saratchandran P,et al.A fast and accurate online sequential learning algorithm for feedforward networks[J].IEEE Transactions on Neural Networks,2006,17(6):1411-1423.
[18] Zong W W,Huang G B,Chen Y.Weighted extreme learning machine for imbalance learning[J].Neurocomputing,2013,101:229-242.
[19] Yu Q,Miche Y,Eirola E,et al.Regularized extreme learning machine for regression with missing data[J].Neurocomputing,2013,102:45-51.
[20] Man Z H,Wang D H,Cao Z W,et al.Robust single-hidden layer feedforward network-based pattern classifier[J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(12):1974-1986.
[21] Peng Y,Lu B L.Discriminative graph regularized extreme learning machine and its application to face recognition[J].Neurocomputing,2015,149:340-353.
[22] Huang G,Song S J.Semi-supervised and unsupervised extreme learning machines[J].IEEE Transactions on Cybernetics,2014,44(12):2405-2417.
[23] Benoit F,van Heeswijk M,Miche Y,et al.Feature selection for nonlinear models with extreme learning machines[J].Neurocomputing,2013,102:111-124.
[24] Kasun L L C,Huang G B,Zhou H M.Representational learning with ELMs for big data[J].IEEE Intelligent Systems,2013,28(5):31-34.
[25] 韩敏,李德才.基于替代函数及贝叶斯框架的1范数ELM算法[J].自动化学报,2011,37(11):1345-1350.
[26] Huang G B.An insight into extreme learning machines:random neurons,random features and kernels[J].Cogn Comput,2014,6:376-390.
[27] 徐挺,刘伟,李传富,等.基于Demons的微分同胚非刚性配准研究[J].北京生物医学工程,2009,29(1):50-52.
[28] Zhang T H,Tao D H.Patch Alignment for Dimensionality Reduction[J].IEEE Transactions On Knowledge and Data Engineering,2009,21(9):1299-1313.
[29] He X F,Niyogi P.Locality preserving projections[C].Advances in neural information processing systems,2004:153-160.
[30] Zong W W,Huang G B.Face recognition based on extreme learning machine[J].Neurocomputing,2011,74:2541-2551.
[31] Chen X M,Liu W Q,Lai J H.Face recognition via local preserving average neighborhood margin maximization and extreme learning machine[J].Soft Comput,2012,16:1515-1523.
[32] Iosifidis A,Tefas A.Minimum Class Variance Extreme learning machine for Human Action Recognition[J].IEEE Transactions on Circuits and Systems for Video Technology,2013,23(11):1968-1979.
FACE RECOGNITION USING OPTIMIZED EXTREME LEARNING MACHINE BASED ON DIFFEOMORPHISM
Li Li’na Yan Deqin Chu Yonghe
(SchoolofComputerandInformationTechnology,LiaoningNormalUniversity,Dalian116081,Liaoning,China)
Extreme learning machine (ELM) has been widely applied in the field of pattern recognition for its efficient and good generalization ability. However, the current ELM and its improved algorithm have not considered the effect of hidden layer nodes’ output matrix on the generalization ability of extreme learning machine. Through experiments we find that when the activation function is improperly selected and the data sample dimension is too high, it will result in output value of hidden layer node tending to zero. It comes to make the solution of output weight matrix inaccurate and reduce the classification performance of ELM. In order to solve these problems, an optimized extreme learning machine algorithm based on diffeomorphism is proposed. The algorithm combines techniques of diffeomorphism and dimensionality reduction to improve the robustness of activation functions and overcome the problem that the output value of hidden layer nodes tends to zero. In order to evaluate the validity of the proposed algorithm, face data is used to implement experiments. Experimental results show that the proposed algorithm has a good generalization performance.
Extreme learning machine Activation function Diffeomorphism
2016-03-22。国家自然科学基金项目(61105085,61373127)。李丽娜,硕士生,主研领域:数据降维,机器学习。闫德勤,教授。楚永贺,硕士生。
TP18
A
10.3969/j.issn.1000-386x.2017.04.029
